+1 (202) 780-3397
Editorial - Research and Reports in Immunology (2018) Timely Topics in Clinical Immunology- Vol II
The importance of reliability in clinical research
David Trafimow*
Department of Psychology, New Mexico State University, Las Cruces, New Mexico
- Corresponding Author:
- David Trafimow
Department of Psychology
New Mexico State University
P.O. Box 30001/MSC 3452, Las Cruces, New
Mexico-88003
USA
Tel: 575-646-4023
E-mail: dtrafimo@nmsu.edu
Accepted on January 25, 2018
Citation: Trafimow M. The importance of reliability in clinical research. Timely Top Clin Immunol. 2018;2(1):1
Editorial
The reliability of dependent variables is an issue whose importance is dramatically underestimated in clinical research. Although clinical researchers know that it is important to have valid measures, there is insufficient understanding of the role that reliability plays in correlative validity-the extent to which variables are capable of correlating with each other. The present goal is to be specific about the role that reliability plays with respect to validity. Nor is this a new topic, as important details have been known for over a century. Charles Spearman provided a seminal contribution by working out the precise relation, expressed in modern symbols, as Equation 1 below 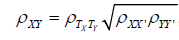[1]:
(1)
where ρXY , is the observed correlation between two variables, ρTXTY is the true correlation or correlation that would be observed with perfect measurement reliability, ρXX and ρYY are the reliabilities of the measures of the two variables.
It is possible to “correct” or “dis-attenuate” for lack of reliability by algebraic rearrangement as follows:
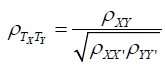(2)
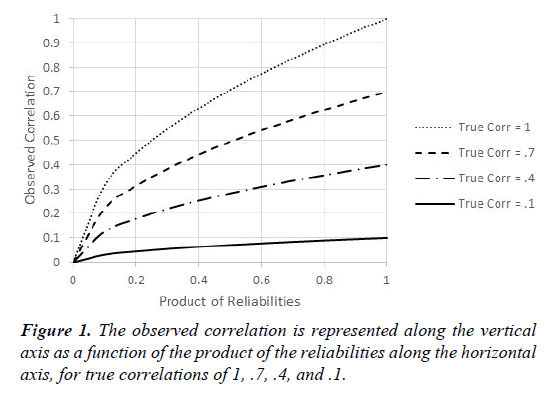
The reason this is important for clinical research can be seen easily by instantiating the value of 0 for either ρXX or ρYY in Equation 1. The result is that no matter the true correlation, the observed correlation is zero. Moving to the other extreme, suppose that the reliabilities of the measures of both variables are equal to 1. In that case, the observed correlation equals the true correlation, which is ideal. Figure 1 below shows how the product of the reliabilities influences the correlation that can be expected to be obtained. Put another way, Figure 1 shows how much true correlations can be expected to attenuate, based on the product of the reliabilities.
Figure 1: The observed correlation is represented along the vertical axis as a function of the product of the reliabilities along the horizontal axis, for true correlations of 1, .7, .4, and .1.
The four curves in Figure 1 refer to true correlations of 1, .7, .4, or .1, respectively, and illustrate how these true correlations are attenuated by having unreliable measures. Moving from right to left, as in many Semitic languages, Figure 1 shows that when the reliabilities are perfect, observed correlations equal true correlations, but lack of reliability can have dramatic deleterious effects on the correlations that can be expected to be obtained, even with reasonably large true correlations. Many researchers consider .7 to be a respectable number for the reliability of a measure, in which case the product of two measures at this level would be .49. If the true correlation is .4, then the implication of Equation 1 is that the obtained correlation will be .28. Whereas .4 might be considered a moderately impressive value, the same cannot be said for .28. More generally, clinical researchers should do everything possible to develop more reliable measures. And in the many cases where reliabilities are low or moderate, researchers need to take that into account when reporting and evaluating research. One way of taking reliabilities of measure into account is to use Equation 2 to dis-attenuate to obtain a better estimate of the true correlation between the variables of interest.