Research Article - International Journal of Respiratory Medicine (2022) Volume 7, Issue 1
Death rate in SARS-CoV-2 under mechanical ventilation: What influences?
Luciano Franck C*
Faculdade Evangélica Mackenzie do Paraná, Hospital das Clinicas at Universidade Federal do Paraná, Brazil
- *Corresponding Author:
- Luciano Franck C
Faculdade Evangélica Mackenzie do Parana
Hospital das Clinicas at Universidade Federal do Paraná, Brazil
Tel: 5541991156085
E-mail: claudiolfranck@hotmail.com
Received: 10-Feb-2022, Manuscript No. AAIJRM-22-54057; Editor assigned: 11-Feb-2022, PreQC No. AAIJRM-22-54057 (PQ);
Reviewed: 18-Feb-2022, QC No. AAIJRM-22-54057; Revised: 21-Feb-2022, Manuscript No. AAIJRM-22-54057 (R); Published: 28-Feb-2022, DOI:10.35841/AAIJRM-7.1.105
Citation: Franck LC. Death rate in SARS-CoV-2 under mechanical ventilation: what influences? Int J Respir Med. 2022;7(1):105
Abstract
Introduction: The Acute Respiratory Distress Syndrome caused by the Coronavirus 2019 (SARSCoV-2) may associate the Acute Respiratory Distress Syndrome (ARDS) and the Ventilation Induced Lung Injury (VILI). However, there are still doubts about the potential damage generators and its influence onpatient outcome. Objective: To analyze the mechanical ventilation and the factors that influence the mortality in SARS-CoV-2. Assess the outcomes based on age, on parameters of the mechanical ventilator, on Mechanical Power and on its fragments through univariate and multivariate analysis of age, Peep, Driving Pressure, elastance and Mechanical Power. Method: Observational, longitudinal, analytical and quantitative study of age and of the parameters of the mechanical ventilator, alongside the calculous of the Mechanical Power and its components of patients with SARS-CoV-2. Results: We identified significant impact on the outcome in the univariate analysis of age (p<0.001), respiratory rate (p=0.047), elastance (p<0.001), complacency (p<0.001), driving pressure (p<0.001), inspiratory pressure variation (p<0.001), peak pressure (p=0.009), plateau pressure (p<0.013), Peep (p<0.001), dynamic elastic power (p<0.001) and static elastic power (p=0.005). In the multivariate analysis the increase in age (p<0.001), in elastance (p=0.0029) and in Mechanical Power (p=0.023), and the reduction in Peep (p=0.044) showed significant impact on the death risk. Conclusion: The increase in age and in Mechanical Power - caused by the rise in its dynamic elastic power component, and reduction of its static elastic power factor - influenced the death rate of patients with SARS-CoV-2 under mechanical ventilation. The variance of the elastic power components may reflect adequately the propulsion power required to overcome the rise in elastance and the lack of responsiveness to Peep adjustments.
Keywords
SARS-CoV-2 infection, Mortality, Ventilation induced lung injury, Acute respiratory distress syndrome.
Introduction
It is proposed to diagnose the SARS-CoV-2 infection through the detection of radiologic consolidation in bilateral air bronchogram with peripheral ground-glass opacity, simultaneously with a Partial Arterial Pressure of O2 over Fraction of Inspired O2 ratio (PaO2/FiO2) under 300 mmHg, hypoxemia and respiratory insufficiency with pulmonary inflammation, which can evolve to fibrosis when associated with mechanical ventilation [1]. In 1990, Ventilation Induced Lung Injury (VILI) [2] was defined as the lesion derived from the application of mechanical powers and from the transfer of energy to the lung tissue that causes inflammation. ARDS and VILI intertwine in a unique and complex manner, in such a way that the contribution of each to the lethality of patients is indistinguishable [3]. Therefore, it is not possible to clinically disconnect the VILI from the underlying process that causes the ARDS, even though the progressive reduction of recruit able (through Peep) and total lung volume allows its empirical prediction [4].
The injury produced by the flow energy is determined by the pressure gradient and by the resulting alveolar deformity, Stress and Strain, respectively [5]. The understanding of the biophysical causes of VILI has redirected the attention from the inflation pattern related to the tidal volume and pressures to the exposition of the alveolar-capillary membrane to damaging levels of energy and power [4].
The generation of VILI depends on the vulnerability of the lung tissue [6], therefore, it would be interesting to determine the defining aspect of the VILI brought by each variable [7]. The risk of VILI increases with the reduction in pulmonary ventilated area and with the resulting rise in damaging tidal cycles. Thus, it is pressing to treat the underlying injury that causes the mechanical alterations in the lung and to allow enough tissue recovery to prevent the injury, otherwise it will result in the inevitable and irrecoverable vortex of VILI [4].
Controversies persist regarding the best oxygenation and ventilation strategies for patients with ARDS caused by SARS-CoV-2 that avoid increases in the presence of VILI. The protective ventilation strategy is applied when tidal volume is kept between 4 and 8 ml/Kg of predicted weight, plateau pressure is lower than 30 cm H2O, driving pressure is lower 15 cm H2O [8] and Peep is maintained between 8 and 14 cm H2O [9].
The modern concept of protective mechanical ventilation allows a parametric excess only during the initial critical care, requiring the minimization of ventilation parameters as soon as the clinical status of the patient stabilizes [10]. This procedure is justified based on the understanding that the inadequate application of the mechanical force with elevation of its components respiratory rate, tidal volume, pressures and flow rises the levels of Mechanical Power, compromising the purpose of resting the lungs promoted by the mechanical ventilation, worsening outcomes by raising the risk of VILI [11,12]. Mechanical Power is a physiological concept that aims to simplify the analysis of mechanical ventilation by depicting it through the collective of the components of the mechanical ventilation [2-11], as well as the injury produced by the energy originated in the pressure gradient that promotes alveolar deformation 5. Made of plateau pressure, driving pressure, Peep, tidal volume, flow, resistance, elastane and respiratory rate [13,14], Mechanical Power depicts the energy transferred to the respiratory system by the mechanical ventilator [13] during a certain period, in Joule per minute (J/ min) [11-15].
Even though there is a tendency to replace the concepts based on tidal volume and pressures in the tidal cycle for the understanding of Mechanical Power as generator of VILI, its predictorial precision is still alleged [16,17], once there are patients submitted to potential VILI generating tidal volume and pressures that survive, making the correlation between ventilatory strategy and clinical status still questionable [18]. Still, lower levels of Mechanical Power are aimed [19], once it unifies the components of the mechanical ventilation in the attempt to build a unity of indicators that reflect VILI [11]. However, none of the components can be set apart as the one responsible for the generation of VILI, once it derives from the set ups of the mechanical ventilation and the characteristics of the lung parenchyma, including its size, vascular pressure, and degree of heterogeneity [18-20]. The protective mechanical ventilation strategies in ARDS intend to reduce the chances of VILI, however it is still unclear the contribution of each component [21] of the mechanical ventilation to the higher risk of VILI.
The quantitative fragmentation of the energy required to inflate the lungs may point to protective ventilation strategies effective to the reduction of the risk of VILI [16], and may clarify the contribution of each component of the power to the generation of such injury. The product of the tidal volume per plateau pressure defines total elastic power [17], which is subdivided in dynamic elastic power and static elastic power. The first one is equal to the energy necessary to inflate the lungs, whereas the second is the energy required to balance out the potential energy stored in the respiratory system by the Peep [22]. The total inflation energy, that is, the Mechanical Power is equal to the total elastic power plus the total kinetic power [17], which is the energy spent on overcoming the airway e tissue resistance to the flow [22]. The product of these equations by the respiratory rate and by the conversion constant 0.098 results in Joules per minute.
This study aims to analyze the interference of the mechanical ventilation on the outcomes of patients with moderate ARDS caused by SARS-CoV-2 under mechanical ventilation, to find the average value of energy applied by the ventilator through the Mechanical Power, to compare the outcomes of discharge and death with the components of the mechanical ventilation, and to determine Mechanical Power and its subdivisions in SARS-CoV-2 through the implementation of univariate and multivariate analysis of age, Peep, driving pressure, elastance and Mechanical Power.
Methods
Longitudinal, observational, analytical, and quantitative study of the information collected from the ventilation parameters of patients with moderate ARDS caused by SARS-CoV-2 admitted to an intensive care unit in a university hospital made a reference in this Ethics Committee in Research of the Clinical Hospital of the Federal University of Paraná, in the process numbered 4.571.036.
As an inclusive criterion for the data collection of patients, it was required a 6 or 7 in the OMS scale of gravity, a partial arterial pressure of O2 over the fraction of inspired O2 ratio between 100 and 200 mmHg, thorax radiography or computed tomography showing bilateral opacities and D-dimer within normal limits with RT-PCR confirming the SARS-CoV-2 infection.
There were a total of 147 samples of patients with moderate ARDS and SARS-CoV-2 that remained intubated in volumecontrolled ventilation in a Puritan Bennet TM840® under deep sedation and analgesia and neuromuscular blocking agents (NMBA). A total of 1029 components of mechanical ventilation were documented, and we chose to collect the parameters every 3 days to establish the average Mechanical Power required by the SARS-CoV-2 throughout the patient stay.
On the other hand, in the analysis for comparison of outcomes, we documented the last parameters of the mechanical ventilation and calculated Mechanical Power and its subdivisions just before the suspension of the NMBA or the death of the patient.
We transcribed the Respiratory Rate (RR), Tidal Volume (Vt), Inspiratory Flow (Finsp), inspiratory time (Tinsp), expiratory time (Texp), average pressure (Pmedia), peak pressure (Ppeak), plateau pressure (Pplateau) through the inspiratory pause and intrinsic Peep (PeepI) through the expiratory pause. From these data, we generated minute volume (Ve), driving pressure, resistive pressure (Presist), static complacency (C), elastance (E), inspiratory resistance (Rinsp) expiratory resistance (Rexp), expiratory flow (Fexp) and Mechanical Power [23].
• Mechanical Power = 0.098.Fr.Vt.[PPico–0,5(PPlateau–peep)] Mechanical Power was subdivided [22] and each part was multiplied by the respiratory rate and the conversion constant 0.098, so that it would be possible to determine its values in Joules per minute (J/min):
• Dynamic elastic power =0.098.RR.Vt.(0,5.E.Vt2)
• Static elastic power =0.098.RR.(Vt.Peep)
• Inspiratory flow resistive power =0.098.RR.(Vt2.R /Tinsp)
These results were transcribed to an Excel® spreadsheet and the subsequent statistical analyses were performed in a data processing system by IBM SPSS Statistics v.20.0. Armonk, NY: IBM Corp, Stata/SE 14.1, Stata Corp LP, USA. Then, the results were discussed regarding previously published articles.
Statistical Analysis
The univariate analysis of the physiological variable age was applied alongside the same analysis of each parameter of the mechanical ventilator and of its unity represented in Mechanical Power, which was subdivided in its components dynamic elastic power, static elastic power and inspiratory flow resistive power.
There was also a multivariate analysis of the physiological variable age alongside the same analysis for the static and elastic components of the mechanical ventilation represented by Peep and driving pressure, respectively, been the later determined by the resistance from the elastance and by the energy required to inflate the lungs, thus, Mechanical Power. For the description of the quantitative variables, statistics of average, median, minimal, and maximal values and standard deviation were considered. For the comparison of the two possible outcomes regarding their relation to the quantitative variables, at Student Test was performed for independent samples. The estimation of Pearson’s Correlation Coefficient was considered for the analysis of association between the quantitative variables. To evaluate the impact of the collective association of variables on the outcome, a model of Logistic Regression was adjusted, estimating the Odds Ratio of each variable while maintaining constant the remaining ones included in the model. The model adjustment was conducted based on the Hosmer and Lemeshow ‘s test. Finally, the p values under 0.05 indicated statistical significance.
Results
1029 calculus of Mechanical Power were made from the data of 147 patients with SARS-CoV-2 for the time they were intubated for the maintenance of mechanical ventilation in volume-controlled ventilation under deep sedation and analgesia and using neuromuscular blocking agents. The average value of Mechanical Power was 26.71 J/min, which is close to the average value of 26.60 J/min found in the 147 samples collected just before the withdrawal of NMBA or death of each patient that met the criteria for inclusion in this study.
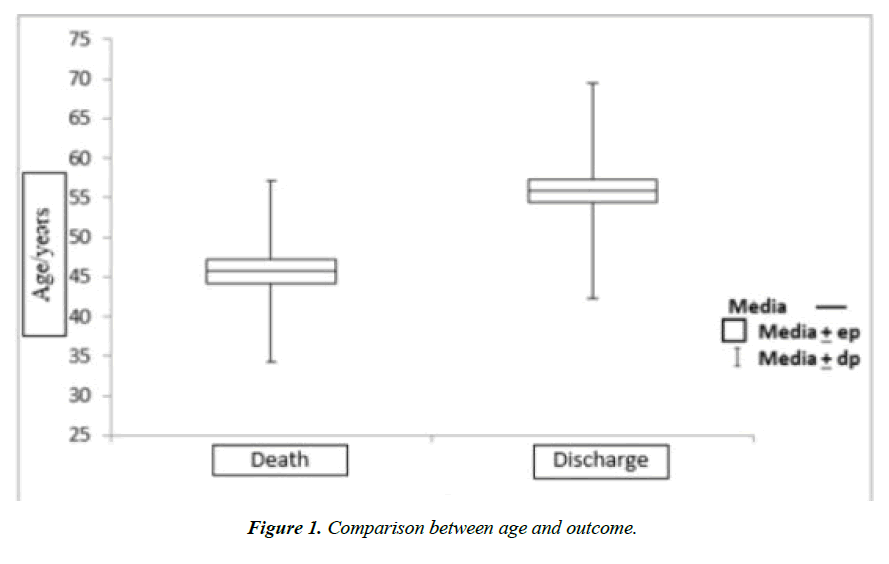
The average length of stay in the ICU was 21 days, with minimal of 7 days and maximum of 56 days. Amongst the 147 patients included in this study, the estimated mortality was of 63.9%, with 94 deaths and 53 discharges, of which 25 were female (37.90%) and 28 were male (34.50%) patients. The total data was composed of 81 male patients (55.10%) and 66 female patients (44.90%) with minimal age of 20, maximum age of 79, and average age of 52.2 years old. In the univariate analysis an average age of 45.7±11.4 years of age was observed in the discharged population, while an average of 55.9±13.6 years of age was witnessed in the population that died (p<0.001) as shown in (Figure 1).
In the analysis of each component of the mechanical ventilation, the null hypothesis of equal averages of discharge and death versus the alternative hypothesis of different averages were tested. In (Table 1), for each outcome, the descriptive statistics are outlined considering the results of each variable obtained in this study.
| Variable | Outcome | n | Mean | Median | Min. | Max. | Standard Deviation | p-value |
|---|---|---|---|---|---|---|---|---|
| Insp (L/min) |
Discharge | 53 | 53.3 | 54.0 | 35 | 74 | 8.9 | 0.903 |
| Death | 94 | 53.1 | 53.5 | 24 | 82 | 8.9 | ||
| Complacence (L/cmH2O) | Discharge | 53 | 0.034 | 0.034 | 0.016 | 0.060 | 0.010 | < 0.001 |
| Death | 94 | 0.027 | 0.023 | 0.009 | 0.077 | 0.013 | ||
| Vt (L) |
Discharge | 53 | 0.35 | 0.36 | 0.25 | 0.50 | 0.06 | 0.367 |
| Death | 94 | 0.34 | 0.34 | 0.23 | 0.54 | 0.06 | ||
| Ve (L/MIN) |
Discharge | 53 | 11.32 | 11.20 | 7.56 | 17.00 | 2.12 | 0.890 |
| Death | 94 | 11.37 | 10.85 | 7.68 | 18.20 | 2.13 | ||
| RR/min | Discharge | 53 | 32.0 | 32.0 | 25 | 36 | 3.1 | 0.047 |
| Death | 94 | 33.1 | 35.0 | 22 | 37 | 3.0 | ||
| PPeak (cmH20) |
Discharge | 53 | 29.4 | 29.0 | 22 | 38 | 3.7 | 0.009 |
| Death | 94 | 31.3 | 31.0 | 20 | 48 | 4.9 | ||
| ΔInsp (cmH20) |
Discharge | 53 | 15.0 | 15.0 | 7.0 | 24.5 | 3.1 | < 0.001 |
| Death | 94 | 19.5 | 18.3 | 8.0 | 42.0 | 5.7 | ||
| Plateau (cmH20) |
Discharge | 53 | 25.4 | 25.0 | 19 | 31 | 2.9 | 0.013 |
| Death | 94 | 27.0 | 27.0 | 17 | 44 | 4.6 | ||
| Resist (cmH20) |
Discharge | 53 | 4.0 | 4.0 | 1 | 10 | 2.1 | 0.343 |
| Death | 94 | 4.3 | 4.0 | 2 | 10 | 1.8 | ||
| ΔP (cmH20) |
Discharge | 53 | 11.0 | 11.0 | 5.0 | 22.5 | 3.1 | < 0.001 |
| Death | 94 | 15.2 | 14.3 | 5.0 | 38.0 | 5.7 | ||
| Peep (cmH20) |
Discharge | 53 | 14.4 | 15.0 | 6.3 | 20.0 | 3.3 | < 0.001 |
| Death | 94 | 11.8 | 11.0 | 5.0 | 21.0 | 4.0 | ||
| Peep I (cmH20) |
Discharge | 53 | 0.8 | 0.7 | 0 | 2.7 | 0.5 | 0.504 |
| Death | 94 | 0.7 | 0.6 | 0.2 | 2.4 | 0.4 | ||
| TInsp (s) |
Discharge | 53 | 0.76 | 0.74 | 0.66 | 1.00 | 0.06 | 0.237 |
| Death | 94 | 0.75 | 0.74 | 0.60 | 1.00 | 0.07 | ||
| TExp (s) |
Discharge | 53 | 1.13 | 1.06 | 0.95 | 1.58 | 0.17 | 0.087 |
| Death | 94 | 1.08 | 1.01 | 0.90 | 1.73 | 0.16 | ||
| Elastance (cmH2O/L) |
Discharge | 53 | 31.84 | 29.27 | 1667 | 62.50 | 10.27 | < 0.001 |
| Death | 94 | 45.97 | 44.28 | 12.96 | 106.67 | 19.78 | ||
| FExp (l/min) |
Discharge | 53 | 19.19 | 18.31 | 11.83 | 31.25 | 4.09 | 0.689 |
| Death | 94 | 19.47 | 19.18 | 11.85 | 30.89 | 3.98 | ||
| RInsp (cmH2O/L/min) |
Discharge | 53 | 0.142 | 0.130 | 0.030 | 0.361 | 0.069 | 0.163 |
| Death | 94 | 0.159 | 0.138 | 0.056 | 0.444 | 0.072 | ||
| RExp (cmH2O/L/min) |
Discharge | 53 | 0.040 | 0.039 | - | 0.096 | 0.025 | 0.347 |
| Death | 94 | 0.037 | 0.031 | 0.008 | 0.148 | 0.022 | ||
| PMedia (cmH20) |
Discharge | 48 | 19.4 | 19.0 | 14.0 | 25.0 | 2.8 | 0.472 |
| Death | 88 | 19.0 | 18.0 | 12.0 | 28.0 | 3.5 |
Table 1 .Comparison between each variable and the outcome.
Regarding the comparison between the outcomes discharge and death, in (Table 1), respiratory rate (p=0.047), the variables derived from the pulmonary conditioners elastance (p<0.001) and complacency (p<0.001), as well as the pressure variables driving pressure (p<0.001), inspiration pressure variation (p<0.001), peak pressure (p=0.009), plateau pressure (p<0.013) and Peep (p<0.001) showed statistical significance. The importance of Stress is more clearly evidenced by the relevant difference in its values between the outcomes death and discharge, except for the mean pressure (p=0.472), resistive pressure (p=0.343) and intrinsic Peep (p=0.504). In contrast, tidal volume (p=0.367), minute volume (p=0.890) equal to the product between tidal volume and respiratory rate - the inspiratory and expiratory flows, inspiratory and expiratory resistances and the inspiratory (p=0.237) and expiratory (p=0.087) times did not present statistical significance.
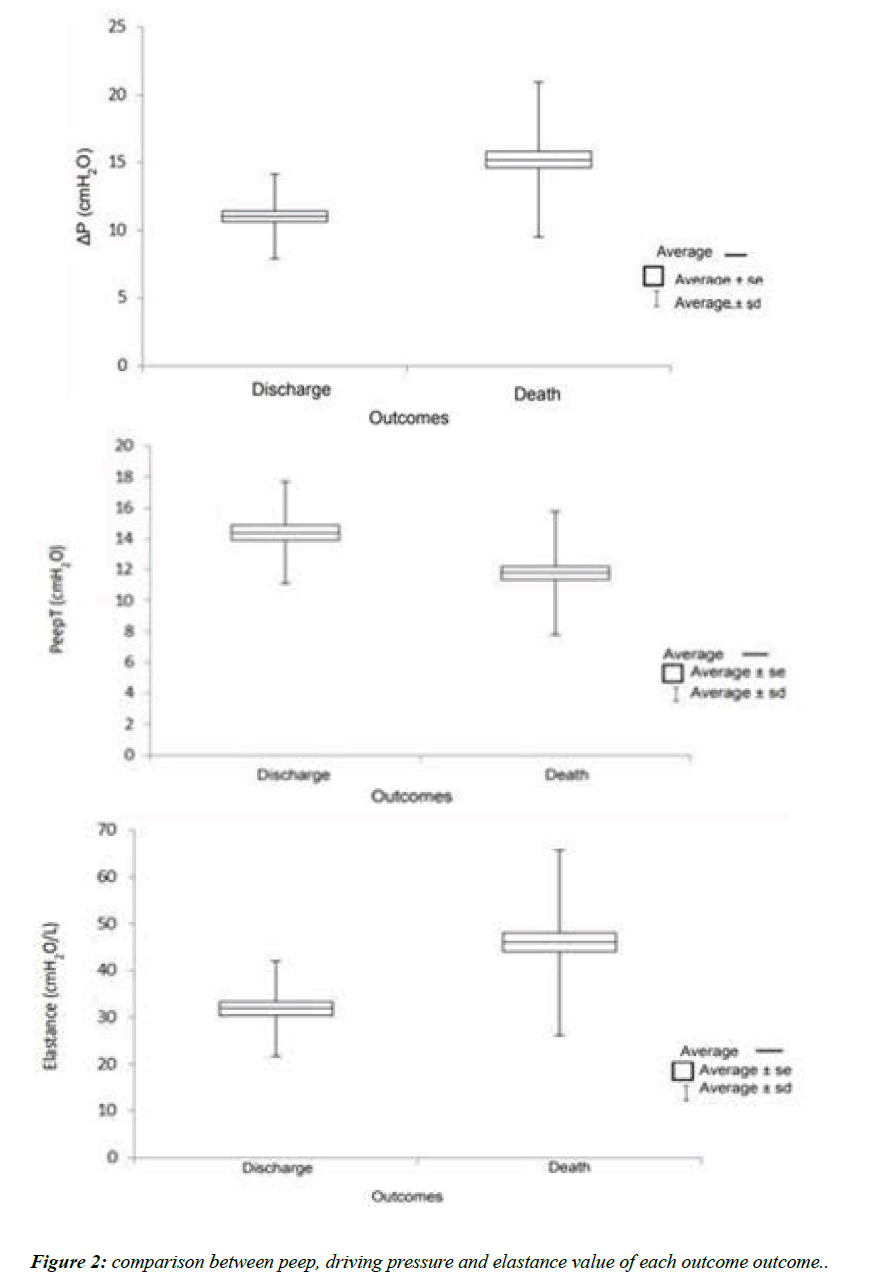
A box diagram depicting the interference of the static elastic and dynamic elastic components Peep and driving pressure, respectively and the need of Stress to promote Strain, represented by the elastance, are highlighted in (Figure 2).
After analyzing the components of mechanical ventilation separately, the set of them unified in the form of energy by Mechanical Power was analyzed. In (Table 2), the univariate analysis of the influence of Mechanical Power on the outcomes shows no statistical significance (p=0.864). However, to better understand the features of the total inspiratory energy, Mechanical power was subdivided in its three factors: inspiratory flow resistive power resulting in dissipation of heat, dynamic elastic power propulsion energy of the driving pressure required to overcome de elastance and static elastic power applied by Peep in order to avoid the collapse of the alveoli.
| Variable (J/min) |
Outcome | n | Media | Median | Min. | Max. | Standard Deviation | p-value |
|---|---|---|---|---|---|---|---|---|
| Mechanical Power or Total Inspiratory Energy | Discharge Death |
53 94 |
26.80 26.58 |
25.24 24.96 |
15.83 13.72 |
44.98 50.01 |
7.59 50.01 |
0.864 |
| Elastic Energy Dynamic Inflation | Discharge | 53 | 6.17 | 5.93 | 2.21 | 13.89 | 2.25 | < 0.001 |
| Death | 94 | 8.41 | 7.76 | 1.96 | 24.11 | 3.51 | ||
| Inspiratory Flux Resistance Energy | Discharge | 53 | 4.56 | 3.81 | 0.83 | 11.66 | 2.73 | 0.562 |
| Death | 94 | 4.81 | 4.51 | 1.51 | 11.11 | 2.18 | ||
| Static Elastic Energy | Discharge | 53 | 16.07 | 15.61 | 6.27 | 27.59 | 5.07 | 0.005 |
| Death | 94 | 13.36 | 11.71 | 5.35 | 33.34 | 5.84 |
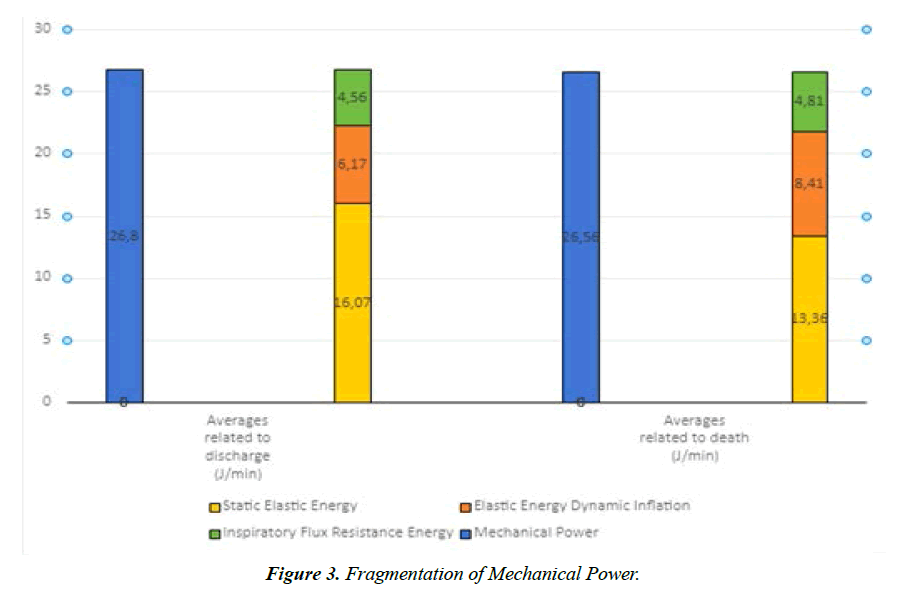
Table 2. Fragmentation of Mechanical Power.
In the analysis of each variable, the null hypothesis of equal averages of discharge and death versus the alternative hypothesis of different averages were tested. (Table 2) shows the descriptive statistics for each variable considering its results obtained in this study, as well as the p value of the statistical test, significant if lower than 0.05. When separate, both the dynamic elastic power (p<0.001) and the static elastic power (p=0.005) varied according to the outcome. Patients that died presented higher values of dynamic elastic power (p<0.001) and lower static elastic power (p=0.005) when compared to these energetic variables of the group of patients that got discharged, as shown in (Figure 3).
The impact of age, as well as of Peep, driving pressure and elastance all related to static and dynamic energies on the outcome in the univariate analyses, simultaneously with the irrelevance of changes in the unifying concept of Mechanical Power to the outcome moved the execution of a multivariable analysis of these variables. Hence, a model of logistic regression was built so that it would be possible to study the group of the selected variables as a whole and its effect on the outcome. To evaluate the quality of the adjustment, the null hypothesis of adequate explanation of the outcome by the model versus the alternative hypothesis of inadequacy were tested. The result of the statistical test did not indicate rejection of the null hypothesis (p=0.899). The results of this quality analysis are shown in (Table 3).
| Variable | p value | Risk Ranking | Odds Ratio | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Univariate | Multivariate | ||||
| Age (Years) |
< 0.001 | < 0.001 | Maiores idades | 1.063 | (1.029 a 1.099) |
| Driving pressure (cmH20) |
< 0.001 | 0.245 | --- | 1.245 | (0.859 a 1.806) |
| Peep (cmH20) |
< 0.001 | 0.044 | Menores valores | 1.217 | (1.006 a 1.473) |
| Elastance (cmH2O/L) |
< 0.001 | 0.029 | Maiores valores | 1.118 | (1.012 a 1.237) |
| Mechanical Power (J/min) | 0.864 | 0.023 | Maiores valores | 1.134 | (1.018 a 1.263) |
Table 3. Multivariate analysis of age, Peep, driving pressure, elastance and Mechanical Power.
As displayed in (Table 3), when studied alongside the other variables, increases in age (p<0.001) raise the death risk. We estimate that, keeping the other variables constant, for each extra year of age there is an increase of 6.3% in the Odds Ratio of mortality (2.90% to 9.905 - CI 95%). Regarding Peep (p<0.044), alongside the other variables, there is evidence that lower values of Peep rise the risk of death. We estimated that, keeping constant the other factors of the model, for each subtrated unit of Peep there is an increase of 21.7% in the Odds Ratio of mortality (0.60% a 47.3%-CI 95%). For elastance (p=0.029), in the presence of the other variables, greater values elevate the risk of death. We estimate that, keeping the other variables constant, for each unit increase in elastance there is a 11,8% rise in the Odds Ratio of mortality (1.2% to 23.7% - CI 95%).
The values of driving pressure in the analysis of each variable showed impact on the outcome (p<0.001), however in the presence of the other factors there is no evidence of association between this variable and the outcome (p=0.245). In contrast, the values of Mechanical Power showed no influence on the outcomes (p<0.064) in the univariate analysis, whereas in the multivariate analysis there is evidence that higher values of Mechanical Power increase the death risk (p=0.023). We estimate that, kept the other factors constant, for each extra unit of Mechanical Power there is an increase of 13.4% in the mortality’s Odds Ratio (1.8% to 26.3% - CI 95%).
Discussion
A more advanced age seems to consolidate as a factor related to SARS-CoV-2 death. Here we noticed a relevant statistical difference in the outcome between the average ages of 49.5 and 53.1 years [24], a similar fact found in this work except for a larger interval in the difference between the average ages, a divergence seemingly related both to an association between survival and average age of 45.7 years as well as between the evolution to death and average age of 55.9 years. In the multivariate analysis it is estimated that each additional year increases the risk of death.
Regarding Stress, a Peep between 6 and 15 cm H2O could prevent VILI [10], considering protective ventilation the plateau pressure less than 30 cm H2O and driving pressure less than 15 cm H2O [8]. Recently an indifference in mortality with higher or lower values of driving pressures was presented [25], which agrees with the multivariate analysis performed in this work, which did not present an association between this variable and the outcome.
We ranked SARS-CoV-2 patients’ lungs in two ways: high complacence, low elastance and low recruitability to Peep named L; and H those with low complacence, high elastance and good recruitability to Peep [26,27]. Infection aggravation can lead to change in phenotype L to H with high lung weight and extensive pulmonary consolidations [27]. However, this work found that the model parameters of mechanical ventilation close to the time of death diverged from both categories, presenting high elastance and low recruitability to Peep, possibly related to the Irrecoverability Vortex of VILI. One can see how both in the univariate and multivariate analyses there was a stronger relation between risk of death and higher values of elastance and lower values of Peep. Furthermore, in the multivariate analysis, for each unit decrease of Peep a 21.7% increase of death risk was estimated, while for every unit increase of elastance there was an 11.8% increase.
The normalization of Mechanical Power value as a safety threshold for the prevention of VILI would depend on the knowledge of pulmonary volume and its distribution, as well as Stress and Strain on the pulmonary heterogeneity [14-28]. The safety thresholds of Mechanical Power vary according to different pulmonary conditions [11], and because of that the problem resides in establishing and expectation of Mechanical Power values, specific for each factor that leads to pulmonary injury. An elevated Mechanical Power, regardless of the combination of its components can lead to VILI [13] when it overcomes 12 J/min, whereas over 17J/min it is associated with a higher mortality rate [19-29]. And between 19 e 24J/ min denotes the severity of ARDS [29]. This work identified intermediate values of Mechanical Power of 26.71J/min, regardless of evolution time, and 26.60J/min when obtained from the last measurements close to the moment of death or withdrawal of NMBA. Despite the high values, its univariate analysis did not show differences in outcome, whereas the multivariate analysis accused interference in the outcome, further estimating that for every additional unit in Mechanical Power there is an increase of 13.4% on the mortality risk.
The safety threshold for Mechanical Power values beyond which VILI is inevitable [11-14]and whether a Mechanical Power-based mechanical ventilation strategy is able to improve patients’ clinical status [14] are still unknown as it is unclear the contribution of each ventilation parameter for the generation of such pulmonary injury. The total inspiratory power, represented by Mechanical Power, was divided into inspiratory flow resistive power, dynamic elastic power and static elastic power. The collected data indicates that the mean dynamic elastic power values was superior (p<0.001), and the mean static elastic power was inferior (p=0.005) in the group of patients who died in comparison to the same variables of the group that was discharged. Hence, the more critical patients needed a greater propulsion force generated by driving pressure to overcome the elastance of the pulmonary tissue, exhibiting low recruitability through Peep.
The individual potential of Peep, driving pressure, and plateau pressure to cause VILI are still under investigation [6], once this type of lung damage seems to depend not only on the total value of Mechanical Power, but also on the interaction between the component of Mechanical Power, including driving pressure and plateau pressure [17]. VILI is caused by the interaction between Vt, RR, Peep, driving pressure, airway resistance and flow, even though the role of each one of these factors in the context of Mechanical Power are still obscure. This study showed that an elevated respiratory rate was related to a higher mortality, however, flow, resistance and tidal volume did not appear to have an influence on the outcome. One could argue that the adjustment of tidal volume follows the protective ventilation protocol in VCV mode, while driving pressure balances out the elastance momentarily along the changes in pulmonary condition.
However, to set apart a single parameter of mechanical ventilation as the only one responsible for the generation of VILI can be a mistake, once it depends on a combination of factors that bring about the Mechanical Power7 and also depends on the interaction between these components [17], making even harder to establish which one can be more decisive to the generation of such pulmonary injury [6]. Driving pressure depicts the tidal volume contained by the complacency of the respiratory system in each moment [5], while elastance refers to the tendency of a material to resist distension or distortion. In this research, besides age that represents a physiological variable elastance that depicts the pulmonary condition of Strain because of Stress also showed significant impact on the mortality of patients with SARSCoV- 2 both in the univariate and in the multivariate analysis.
Conclusion
The increase in age and in Mechanical Power - with increased dynamic elastic power and decreased static elastic power - influenced the death rate of patients with SARS-CoV-2 under mechanical ventilation. The greater values of dynamic elastic power may reflect the elevated propulsion force needed to overcome the increase in elastance, while the inferior static elastic power may explain the low recruitability to Peep.
References
- Gibson PG, Qin L, Puah SH. COVID-19 acute respiratory distress syndrome (ARDS): clinical features and differences from typical pre-COVID-19 ARDS. Med J Aust. 2020;213(2):54-56.
- Vasques, F, Duscio, E, Pasticci, I, et al. Is the mechanical power the final word on ventilator-induced lung injury?-we are not sure. Ann. Transl. Med. 2018;6(19)395:1-6.
- Silva PL, Ball L, Rocco PRM, et al. Power to mechanical power to minimize ventilator-induced lung injury?. Intensive Care Med Exp. 2019;7(38):1-11.
- MariniJJ, Gattinoni L.Time Course of Evolving Ventilatorinduced Lung Injury: The Shrinking Baby Lung. Crit Care Med. 2020;48(8):1203-09.
- Saffaran S, Das A, Laffey JG, et al. Utility of Driving Pressure and Mechanical Power to Guide Protective Ventilator Settings in Two Cohorts of Adult and Pediatric Patients with Acute Respiratory Distress Syndrome: A Computational Investigation Critical Care Medicine. 2020; 48(7):1001-08.
- Marini JJ, Rocco PRM. Which Component of Mechanical Power is the Most Important in Causing VILI?. Critical Care. 2020;24(39):1-3.
- Vassalli F, Pasticci I, Romitti F, et al. Does Iso-mechanical Power Lead to Iso-lung Damage?: An Experimental Study in a Porcine Model. Anesthesiology. 2020;132(5):1126-37.
- Ferrando C, Suarez-Sipmann F, Mellado-Artigas R. COVID-19 Spanish ICU Network. Clinical features, ventilatory management, and outcome of ARDS caused by COVID-19 are similar to other causes of ARDS. Intensive Care Med. 2020;46(12):2200-11.
- Brochard L, Bersten A. Mechanical Power a Biomarker for the Lung?Anesthesioly. 2019;130(1): 9-11.
- Gattinoni L, Michael Quintel M, et al. Less is More in mechanical ventilation Intensive Care Med. 2020;46:780-82.
- Chi Y, He HW, Long Y. Progress of mechanical power in the intensive care unit. Chin Med J 2020;133(18):2197-04.
- Marini JJ,Chiumello D, Gotti M, et al. Bedside calculation of mechanical power during volume and pressure-controlled mechanical ventilation. Critical Care. 2020;24(417):2-8.
- Serpa Neto A, Deliberato RO, Johnson AEW, et al.Network Investigators. Mechanical power of ventilation is associated with mortality in critically ill patients: an analysis of patients in two observational cohorts. Intensive Care Med. 2018;44(11):1914-22.
- Arnal JM, Saoli M, Garnero A. Airway and transpulmonary driving pressures and mechanical powers selected by INTELLiVENT-ASV in passive, mechanically ventilated ICU patients. Heart Lung. 2020;49(4):427-34.
- Van der Meijden S, Molenaar M, Somhorst P, et al. Calcutation Mechanical Power do Pressure-Controled Ventilation. Intensive Care Med. 2019;45(20):1495-97.
- Marini JJ, Rocco PRM, Gattinoni L. Static and dynamic contributors to VILI in clinical practice: pressure, energy, and power. Am J Respir Crit Care Med. 2019.
- Gattinoni L, Rocco PRM. Estimating the Damaging Power of High-Stress Ventilation Respiratory Care. 2020;65(7):1046-52.
- Marini JJ. Dissipation of energy during the respiratory cycle: conditional importance of ergotrauma to structural lung damage. Curr Opin Crit Care. 2018;24(1):16-22.
- Coppola S, Caccioppola A, Froio S,et al. Effect of mechanical power on intensive care mortality in ARDS patients. Critical Care.2020;24(246):2-10.
- Barnes T, Enk D. Ventilation for Low Dissipated Energy Achieved Using Flow Control During Both Inspiration and Expiration. Trends Anaesth. Crit. Care. 2019;24:5-12.
- Dianti J, Matelski J, Tisminetzky M, et al. Comparing the Effects of Tidal Volume, Driving Pressure, and Mechanical Power on Mortality in Trials of Lung-Protective Mechanical Ventilation. Respiratory Care August. 2020.
- Collino F, Rapetti F, Vasques F, et al. Positive End-expiratory Pressure and Mechanical Power. Anesthesiology. 2019;130:119-30.
- Gattinoni L, Tonetti T, Cressoni M, et al. Ventilator- related causes of lung injury: the mechanical power. Intensive care.2016;42:1567-75.
- Alharthy A, Aletreby W, Faqihi F, et al. Clinical Characteristics and Predictors of 28-Day Mortality in 352 Critically Ill Patients with COVID-19: A Retrospective Study. J Epidemiol Glob Health. 2021;11(1):98-104.
- Schuijt MTU, Schultz MJ, Paulus F, et al. Association of intensity of ventilation with 28-day mortality in COVID-19 patients with acute respiratory failure: insights from the PRoVENT-COVID study. Crit Care. 2021;25(1):283.
- Gattinoni L, Chiumello D, Caironi P, et al. COVID-19 pneumonia: different respiratory treatments for different phenotypes?. Intensive Care Med. 2020;46(6):1099-1102
- Marini JJ, Gattinoni L. Management of COVID-19 Respiratory Distress.2020; 323(22):2329-30.
- Gattinoni L, Marini JJ, Collino F. et al. The future of mechanical ventilation: lessons from the present and the past. Crit Care. 2017;21(183):1-11
- Maiolo G, Collino F, Vasques F, et al.Reclassifying Acute Respiratory Distress Syndrome. Am J Respir Crit. 2018;197(12):1586-95.
Indexed at, Google Scholar, Cross ref
Indexed at Google Scholar, Cross ref
Indexed at Google Scholar, Cross ref
Indexed at Google Scholar, Cross ref
Indexed at Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref
Indexed at, Google Scholar, Cross ref