Research Article - Journal of Neuroinformatics and Neuroimaging (2017) Volume 2, Issue 2
Estimation of Z-thickness and XY-anisotropy of electron microscopy images using Gaussian processes.
Ambegoda TD1*, Martel JNP1, Adamcik J2, Cook M1, Hahnloser RHR11Institute of Neuroinformatics, University of Zurich and ETH Zurich, Switzerland
2Department of Health Sciences and Technology, ETH Zurich, Switzerland
- *Corresponding Author:
- Ambegoda T
Institute of Neuroinformatics
University of Zurich
Switzerland
Tel: +4144 6353037
E-mail: thanuja@ini.ethz.ch
Accepted date: October 17, 2017
Citation: Ambegoda TD, Martel JNP, Adamcik J, et al. Estimation of Z-thickness and XY-anisotropy of electron microscopy images using Gaussian processes. Neuroinform Neuroimaging. 2018;2(2):15-22
Abstract
Serial section electron microscopy (ssEM) is a widely used technique for obtaining volumetric information of biological tissues at nanometer scale. However, accurate 3D reconstructions of identified cellular structures and volumetric quantifications require precise estimates of section thickness and anisotropy (or stretching) along the XY imaging plane. In fact, many image processing algorithms simply assume isotropy within the imaging plane. To ameliorate this problem, we present a method for estimating thickness and stretching of electron microscopy sections using non-parametric Bayesian regression of image statistics. We verify our thickness and stretching estimates using direct measurements obtained by atomic force microscopy (AFM) and show that our method has a lower estimation error compared to a recent indirect thickness estimation method as well as a relative Z coordinate estimation method. Furthermore, we have made the first dataset of ssSEM images with directly measured section thickness values publicly available for the evaluation of indirect thickness estimation methods.
Keywords
Electron microscopy, Section thickness, Sample stretching, Gaussian process regression, Atomic force microscopy.
Introduction
Electron microscopy (EM) has enabled imaging of nano-scale neuroanatomical structures such as synapses. Serial section Scanning Electron Microscopy (ssSEM) and serial section Transmission Electron Microscopy (ssTEM) are used to inspect tissue volumes on the scale of tens to hundreds of micrometers in each dimension. Tissue sections suitable for ssEM typically have a thickness that ranges from 30 nm to 70 nm. These extremely thin serial sections are cut from a resin-embedded specimen using an ultramicrotome equipped with a diamond knife. Usually, there can be variations in thickness from one section to another (up to 20%) [1]. Another EM technique used to obtain volumetric image data is Focused Ion Beam Scanning Electron Microscopy (FIBSEM) which allows milling (virtual sectioning) in the order of 5 nm ∼ 10 nm. The problem of section thickness variation is also observed in FIBSEM data [2].
EM image processing methods commonly implicitly assume isotropy of physical structures along the imaging plane [3]. However, sources of anisotropy (stretching) in the imaging plane include anisotropy intrinsic to the specimen (e.g., structures with a preferred orientation), effects of sample handling and cutting, and imperfections in microscope calibration. We focus on the image analysis problem of determining the overall stretching without distinguishing between the sources of stretching.
In this work, we address estimation of thickness and stretching by learning a function ƒ used to infer the spatial distance between pairs of sections based on image statistics. To compute predictive distributions of spatial distances for new, unseen images we use Gaussian Processes (GPs) to perform nonparametric Bayesian regression. We also use GP regressors to estimate stretching.
Section thickness estimates allow the correction of volume estimates along the z axis (perpendicular to the cutting plane), which is useful for producing more accurate 3D reconstructions of imaged tissue. Furthermore, both section thickness and stretching estimates can improve the density estimation of objects such as synapses (normalized per unit volume). This is particularly useful for comparing tissue volumes that underwent different experimental manipulations.
However, we note that the stretching factor alone cannot give us the original area of regions in the original sample, as it cannot distinguish tissue processing-induced stretching from any intrinsically “stretched” (anisotropic) nature of the original sample. Because these sources cannot be distinguished by analyzing the images alone, such absolute measurements are beyond the scope of this paper.
For any method that uses the known XY resolution to model the absolute spatial distance between sections (including Sporring et al. and our method), it is important to have an estimate of the anisotropy along the XY plane. Such XY anisotropy affects the image statistics along the two axes [4]. If unaccounted for, the disparity of these statistics can introduce inaccuracies in the results obtained by methods that assume similar statistics along the two axes. Our solution to this problem is described in section Estimation of Stretching.
In order to validate the thickness estimates, we have directly measured the thickness of a set of EM sections using atomic force microscopy (AFM). We have made the validation dataset publicly available as a benchmark to evaluate section thickness estimation methods [5].
Validation results and estimates for z-section thickness and xy-anisotropy for FIBSEM, ssTEM and ssSEM data sets are discussed in the following Section.
The code for running the experiments described in this paper is publicly available [6].
Related Work
In [4], the relationship between pairwise image dissimilarity and distance is computed by averaging over discrete data points. The estimated thickness of a new section is interpolated from these. [4] assumes that locally, images are realizations of an isotropic and rotationally invariant process. By contrast, we adopt an approach that is less affected by sample anisotropy in the XY plane.
In [7,8], the positions of the images along the Z axis are iteratively corrected to seek a consistent solution in which adjacent sections have an optimal gap (or thickness) between them. The optimal solution adjusts the positions of the images such that the distance-similarity curve is maximally smooth after a fixed number of iterations.
To keep the section thickness consistent in the FIBSEM milling process, [9] presents a method to infer the section thickness using the intensity of the ion beam that has been used for milling. Moreover, they propose to estimate the section thickness by rescaling Z coordinates such that the peaks of the autocorrelations along the Z axis and the X axis have the same full width at half maximum. However, this method provides an average thickness value for all sections unlike Sporring et al. and our method that estimate thickness for each section individually [4].
An ellipsometric approach was suggested by Peachey [10], where the reflected color of the thin sections floating on water was used to coarsely estimate the thickness of the sections. This method provides a coarse estimate up to an accuracy of 15 nm to 25 nm and the minimum thickness that can be estimated is about 50 nm. Accidental folds in the EM sections are used to determine the thickness of that section [11]. Furthermore, Fiala and Harris [12] proposed the method of cylinders that uses “cylindrical” mitochondria to get an estimate of section thickness under the assumption that cylindrical mitochondria can be found with their axis parallel to the cutting direction.
Estimation of Section Thickness
We propose to learn a function of pairwise image dissimilarity to estimate the distance between a pair of sections. Our approach adapts the work of Sporring et al. with the variation described below [4]. What we refer to as section thickness is the distance between a pair of adjacent sections in a series of volumetric images.
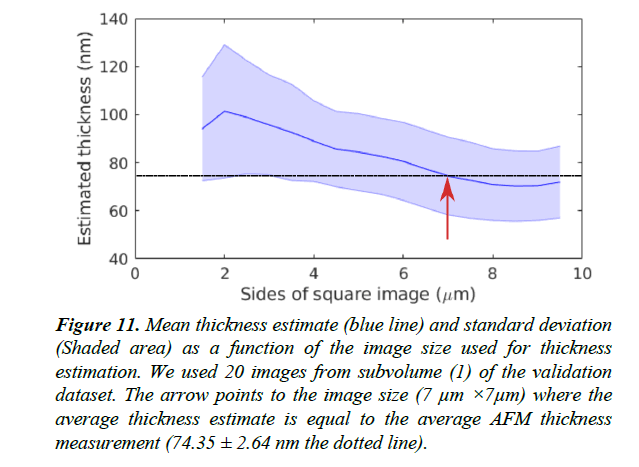
We assume that local structures in the images vary smoothly in all directions at a spatial scale larger than the section thickness. Hence, the dissimilarity SIA ,IB between two parallel images IA and IB only depends on the spatial distance DA,B between them. To learn the variation of image dissimilarity as a function of the distance, we extract images at known distances along the X and Y axes of the imaging plane: DA,B = ƒ(SIA,IB). This can be done by generating two equally sized image patches A and B from any original image I which are a distance DA,B=n×Δx away from each other. Here Δx is the length of a rectangular pixel along the X axis and n is the number of pixels. Image patch A is centered on pixel coordinates (xi,yi), and image patch B is centered on pixel coordinates (xi+n × Δx,yi). We observed that patches smaller than 7 × 7 μm tend to have problems caused by sample inherent anisotropy (e.g., elongated mitochondria, membranes accidentally having similar orientations). The variation of thickness estimates with image size for subvolume (1) of the validation dataset is plotted in Figure 11. The shape of the extracted image patches has no effect on the learned statistics.
As dissimilarity measure SIA,IB , we use the standard deviation of pixel-wise intensity differences (SDI) defined in eqn. (1), similar to Sporring et al. [4].
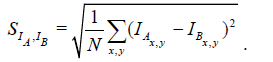 (1)
(1)
We learn two separate distance-dissimilarity functions ƒx (S) and ƒy (S) as described in the section Non-Parametric Bayesian estimation using Gaussian Process regression. After estimating the relative stretching γ between the two axes, we use one of these functions to estimate section thickness depending on the value of γ. Since samples could be compressed in one direction relative to the other due to effects of tissue handling/cutting, we recommend using the distance-dissimilarity function corresponding to the lesser compressed axis for estimation of section thickness.
Non-parametric Bayesian estimation using Gaussian Process Regression
We aim to learn from data the distance D of two images as a function ƒ of image dissimilarity S between pairs of images:
D=ƒ(S). (2)
Given many image pairs, a training dataset consisting of N data points {(Di,Si)}ie{1,…,N} in the distance-dissimilarity plane is created. This general supervised learning framework in which we estimate the function ƒ that best fits these data points is commonly known as regression. The use of a regression model to infer an output (displacement in our case) given an input (our dissimilarity) is usually referred to as prediction.
In regression analysis, a common method to learn ƒ is to assume
a specific form ƒw parameterized by a vector w. Then, the
regression problem can be formulated as finding the best set
of parameters that minimizes a sample loss Li, for all pairs of
outputs Di and inputs Si. As an example, least squares regression
specifies 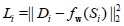 and finds w*, an optimal set of weights
such that w* = argminw
and finds w*, an optimal set of weights
such that w* = argminw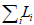 .
.
Here we formulate the regression problem in a Bayesian framework that aims to infer the posterior distribution of the parameters p(w|D,S), given a prior for their distribution p(w) and a likelihood coming from the data p(D|S,w), D=ƒw (S)+ϵ, where ϵ is a noise model. In this view, the mode of the posterior p(w|{Di,Si}i) corresponds to the most likely solution for the regressor, and the standard deviation of the posterior corresponds to the uncertainty.
An intrinsic limitation of parametric regression is the need to explicitly specify ƒw: in many practical problems, this function is a-priori unknown and one might prefer not to make strong assumptions about it.
We formulate the inference problem in function space [13]
using Gaussian Process (GP) regression [14], where a GP is
set of random variables for which any finite subset has a joint
Gaussian distribution. A GP defines a probability distribution
over functions that allows inference in the space of functions.
The GP is completely specified by a mean function m(S) and a
covariance function k(S,S') reflecting the mean and covariance
of the process ƒ, formally: m(S)= 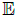 [f(S)] and, k(S,S)=
[f(S)] and, k(S,S)= 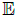 [(f(S)−m(S))(f(S′)−m(S′))], where
[(f(S)−m(S))(f(S′)−m(S′))], where 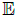 denotes the expectation
w.r.t ƒ. The unknown function ƒ(S) can be seen as a realization
of the Gaussian Process:
denotes the expectation
w.r.t ƒ. The unknown function ƒ(S) can be seen as a realization
of the Gaussian Process:
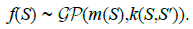 (3)
(3)
To perform regression using a Gaussian Process [15], only the form of the functions m and k have to be specified. These functions do not induce a particular form for ƒ: rather, the covariance function can be seen as specifying a prior over the function space. Also, note that eventual hyperparameters for the mean and covariance function can be learned from data.
For our model, we choose the covariance k (S,S') function to be a squared exponential (SE):
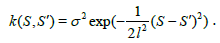 (4)
(4)
Intuitively, an SE covariance is a smoothness prior on the functions determined by the length-scale l and the signal standard deviation parameter σ. For the distance measure SDI we choose a function of the form m(S)=a Sb as the mean function, because the SDI empirically shows a power law increase starting from (0,0).
The set of hyperparameters θ=(σ,l,a,b)T can be seen as
hyperpriors that guide the optimization but are not restrictive.
Both hyperpriors p(a)=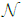 (μa, σa) and p(b)=
(μa, σa) and p(b)= 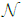 (μa, σa) are
Gaussian distributions whose means (μa, μb) and standard
deviations (σa,σb) are determined using a standard non-linear
regression of a function D'=a·S'b using a Levenberg-Marquardt
algorithm.
(μa, σa) are
Gaussian distributions whose means (μa, μb) and standard
deviations (σa,σb) are determined using a standard non-linear
regression of a function D'=a·S'b using a Levenberg-Marquardt
algorithm.
For the distance measure SDI, we empirically found that the length scale parameter l =10 and the signal variance parameter σ=1 allow the GP to model the desired level of smoothness and robustness to noise by visual inspection of resulting distancesimilarity plots.
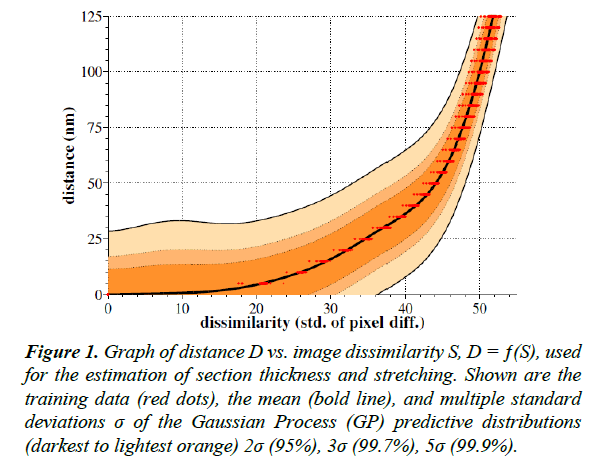
To perform the GP regression itself, we compute the marginal likelihood. We then produce a predictive distribution for the output D at each test input location S. Figure 1 shows the mean and variance of these predictive distributions.
Figure 1: Graph of distance D vs. image dissimilarity S, D = ƒ(S), used for the estimation of section thickness and stretching. Shown are the training data (red dots), the mean (bold line), and multiple standard deviations σ of the Gaussian Process (GP) predictive distributions (darkest to lightest orange) 2σ (95%), 3σ (99.7%), 5σ (99.9%).
Estimation of Stretching
The learned distance-dissimilarity function can be utilized to
estimate the stretching coefficient γyx, defined as the deviation
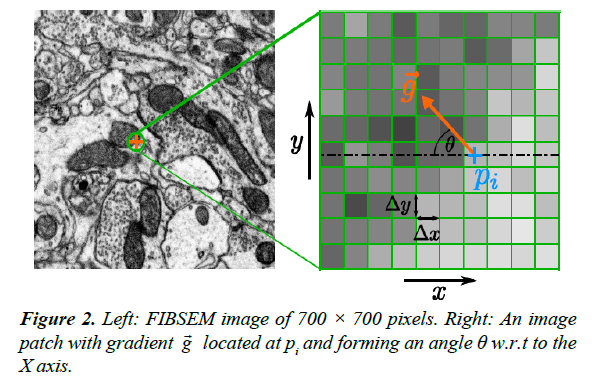
from isotropy of the image along the Y axis relative to the X axis. Consider a small image patch with pixel intensity gradient 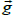 at an angle θ relative to the X axis, Figure 2. The intensity difference Δpi at pixel i between two image patches separated by one pixel (Δ x) along the X axis is given by:
at an angle θ relative to the X axis, Figure 2. The intensity difference Δpi at pixel i between two image patches separated by one pixel (Δ x) along the X axis is given by: 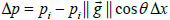 , where pi is the pixel
intensity at pixel i. It follows from eqn. (1) that the dissimilarity
between these image patches (ignoring boundary conditions) is:
, where pi is the pixel
intensity at pixel i. It follows from eqn. (1) that the dissimilarity
between these image patches (ignoring boundary conditions) is:
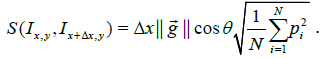 (5)
(5)
As shown by eqn. (5) the dissimilarity is directly proportional to the local gradient of the image patch. We use this result to estimate γ along one axis relative to the other (because stretching along one axis alters the component of the gradient along that axis).
To estimate γ along the Y axis relative to the X axis ( i.e., γyx)
we perform the following steps: First, the distance-dissimilarity
function ƒx(S) is learned using images displaced by n pixels along
the X axis. Then, for a pair of images separated by one pixel
along the Y axis (distance Δy), we calculate the dissimilarity
value S using eqn. (1). Using the value of S, we estimate the
pixel distance using the regression function ƒx(S) learned
above. This estimate gives 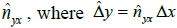 . This is the
expected length of a pixel along the Y axis using the distancedissimilarity
statistics along the X axis. Therefore,
. This is the
expected length of a pixel along the Y axis using the distancedissimilarity
statistics along the X axis. Therefore, 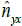 captures
the linear scaling of the Y axis with respect to the X axis in terms of distance-dissimilarity statistics. The stretching coefficient γyx of the Y axis relative to the X axis is defined as
captures
the linear scaling of the Y axis with respect to the X axis in terms of distance-dissimilarity statistics. The stretching coefficient γyx of the Y axis relative to the X axis is defined as
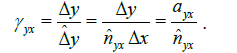 (6)
(6)
where ayx is the pixel aspect ratio Δy / Δx. For a pixel aspect ratio of 1, γyx>1 implies stretching of the Y axis relative to the X axis. Once the γyx is known, we suggest to use the regressor corresponding to higher γ (lower relative compression) as the distance-dissimilarity function for section thickness estimation. For instance, provided γyx < 1, the regressor ƒx(S) should be used because the linear compression of the Y axis is potentially higher than that along the X axis and therefore ƒx(S) will result in a more accurate thickness estimate.
However, the exact orientation of the X and Y axes are arbitrary.
In order to find the directions of maximum and minimum
stretching, γyx has to be calculated for a range of orientations.
The lowest value 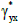 corresponds to the pair of orthogonal axes
for which X has the minimum stretching along its direction.
corresponds to the pair of orthogonal axes
for which X has the minimum stretching along its direction.
Validation of Thickness Estimation using Atomic Force Microscopy
Validation of EM section thickness estimation methods should be performed using a standard data set with accurately measured thickness. We used Atomic Force Microscopy (AFM) [16] to produce a dataset for validation of thickness estimates. AFM is a scanning probe microscopy technique that can be used to measure the 3D surface profile of a section at nanometer resolution. The AFM probe is a sharp tip with a typical radius of 5 ~ 50 nm that scans the surface while measuring changes in the atomic forces between the sample and the tip. AFM allows us to directly measure the thickness of ssEM sections placed on flat silicon wafers (Figure 4).
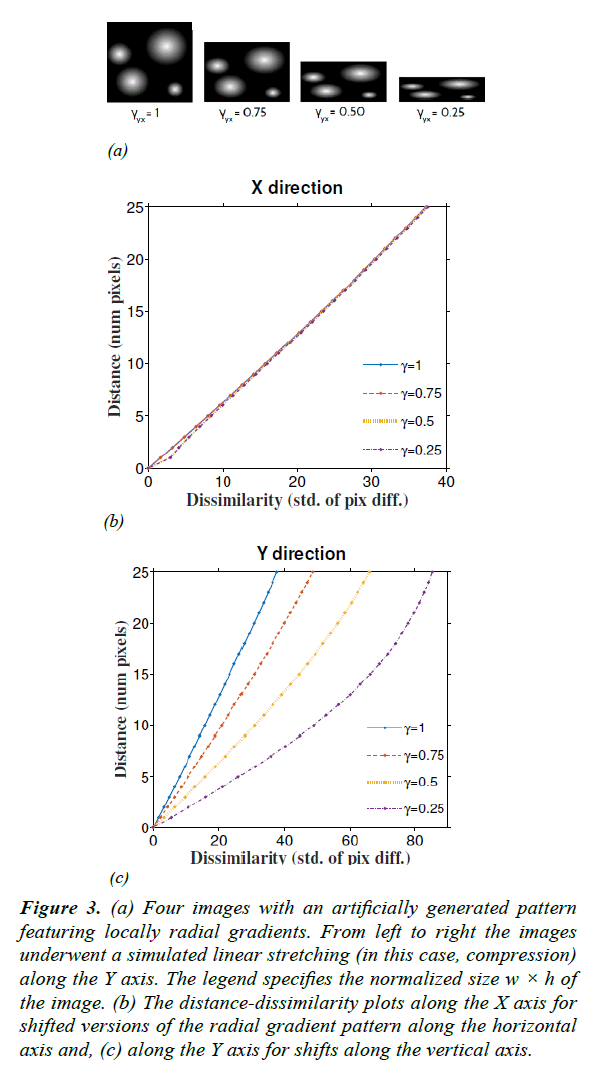
Figure 3: (a) Four images with an artificially generated pattern featuring locally radial gradients. From left to right the images underwent a simulated linear stretching (in this case, compression) along the Y axis. The legend specifies the normalized size w × h of the image. (b) The distance-dissimilarity plots along the X axis for shifted versions of the radial gradient pattern along the horizontal axis and, (c) along the Y axis for shifts along the vertical axis.
An uncertainty analysis for height measurements using AFM has been performed in [17-19]. The uncertainty of the measurements for heights of around 200 nm is reported to be 1 nm whereas for heights below 50 nm the uncertainty is 0.5 nm.
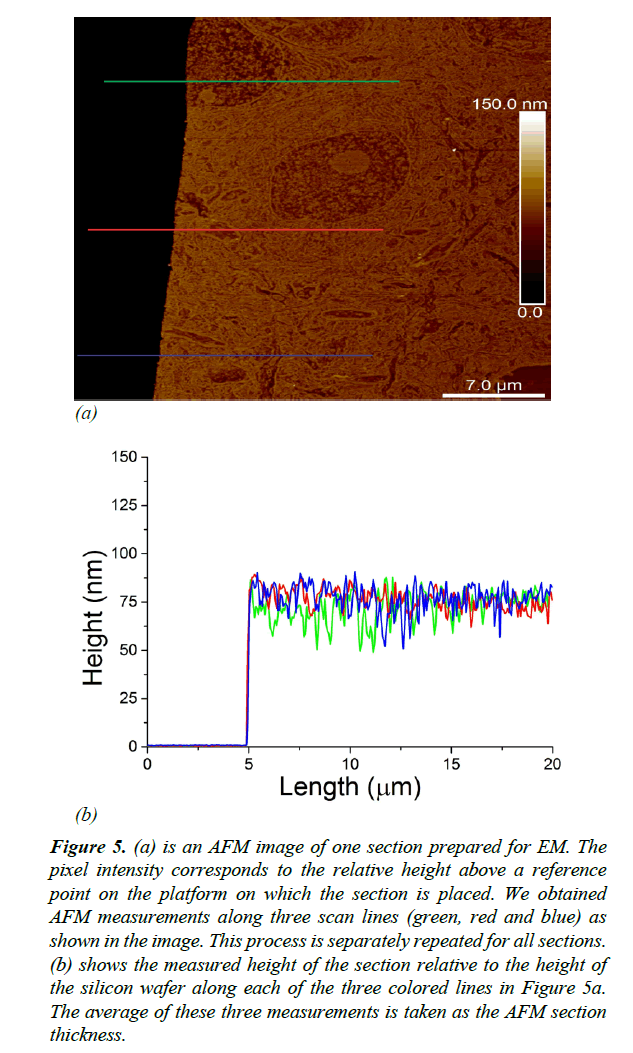
As illustrated in Figure 5a, thickness measurements were obtained using AFM along three distinct scan lines along each ultrathin tissue section. We measured the thickness of each section as the average distance between the surface of the silicon wafer and the surface of the EM section Figure 5b. EM imaging (with parameters: dwell time 7 μs, probe current 500 pA, extrahigh tension (EHT) 1.5 kV) typically mills around 10 nm of tissue. To avoid offsetting the AFM thickness measurements by EM milling, we made sure that EM imaging and AFM measurements were performed on non-overlapping regions on the sections.
Figure 5: (a) is an AFM image of one section prepared for EM. The pixel intensity corresponds to the relative height above a reference point on the platform on which the section is placed. We obtained AFM measurements along three scan lines (green, red and blue) as shown in the image. This process is separately repeated for all sections. (b) shows the measured height of the section relative to the height of the silicon wafer along each of the three colored lines in Figure 5a. The average of these three measurements is taken as the AFM section thickness.
Results and Discussion
To validate the estimation of the stretching coefficient γ, we used linearly compressed versions of a synthetic image as shown in Figure 3a. The original image was composed of bright circular objects with radial gradients. Then the image was rescaled with known γ along the Y axis (vertical) down to different sizes. Using eqn. (7) we recovered γ with an average accuracy of 97.3% for a linear compression of 75% (Table 1).
Table 1. Estimated stretching coefficient γyx in synthetic images (Figure 3), 500 FIBSEM images, and 20 ssSEM images.
| γ for synthetic images (Figure 3) | γ for real images | |||
|---|---|---|---|---|
| Ground-Truth | 0.75 | 0.50 | FIBSEM | 0.94 ± 6.6×10-4 |
| Estimates | 0.730 | 0.63 | ssSEM | 0.86 ± 0.01 |
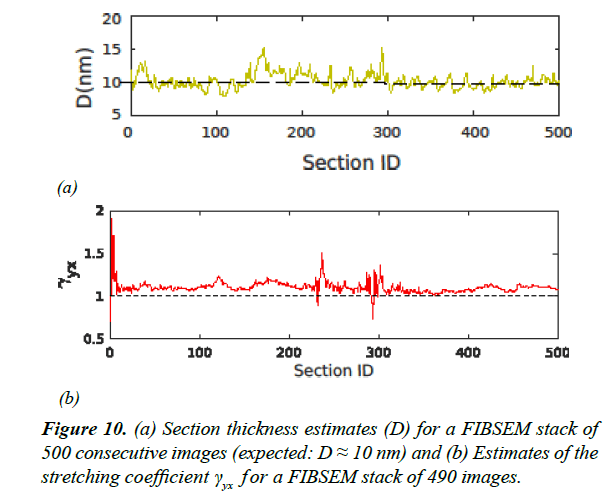
Estimated γ for real data sets (ssTEM [20] and FIBSEM) are summarized in Table 1. The FIBSEM dataset of 490 images was taken from songbird brain tissue imaged at 5 nm × 5 nm resolution along the XY plane and with expected section thickness of 10 nm. The entire FIBSEM stack had the dimensions 8 μm × 8 μm × 5 μm. Estimates of γ and section thickness for the FIBSEM dataset are plotted in Figure 10.
To validate our thickness estimation method, we prepared a dataset of 20 serial sections, taken from the same brain area. Three image stacks were obtained by performing ssSEM on three non-overlapping areas of these sections. The image size of each of these subvolumes are: (1) 9.5 μm × 9.5 μm (2) 6.5 μm × 6.5 μm (3) 6.5 μm × 6.5 μm. The EM images were acquired at a spatial resolution of 5 nm × 5 nm.
We found that the FIBSEM data were associated with a higher γ (lower linear compression) compared to the ssSEM data. This is due to the fact that unlike in ssSEM, FIBSEM does not make use of a diamond knife for thin sectioning, which is a potential source of linear compression. Instead, FIBSEM uses an ion beam to successively burn away thin layers.
The image similarity measures used in our approach and Sporring et al. are based on local deviations of pixel intensities across adjacent sections [4]. Therefore, thickness estimates are sensitive to errors in image registration. For this reason, it is important to make sure that the image stack is properly registered before applying either of these methods for section thickness estimation.
We registered the serial section images into a 3D image volume using elastic alignment [21] that jointly performs 2D stitching, 3D alignment, and deformation correction. This approach is based on an initial alignment obtained by matching image landmarks on nearby sections, where the landmarks are defined using SIFT image features. Further deformations are estimated using local block matching. Afterwards, this initial alignment is optimized by modeling each section as a mesh of springs where parts of the image are allowed to translate and rotate subject to imposed rigidity limits.
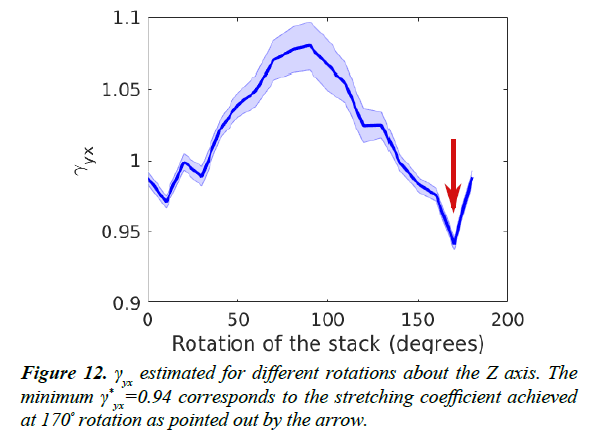
As mentioned in the section titled Estimation of Stretching,
the image axes X and Y are arbitrarily chosen. Therefore,
we estimated the maximum stretching factor 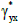 for a range
of possible axes by rotating the original images up to 180º.
Anisotropy estimates for a range of such rotations are shown
in Figure 12. We found that thickness estimation is optimal
when the images are rotated such that the stretching factor γyx is minimized. At this rotation angle, the X axis is minimally
stretched compared to the Y axis.
for a range
of possible axes by rotating the original images up to 180º.
Anisotropy estimates for a range of such rotations are shown
in Figure 12. We found that thickness estimation is optimal
when the images are rotated such that the stretching factor γyx is minimized. At this rotation angle, the X axis is minimally
stretched compared to the Y axis.
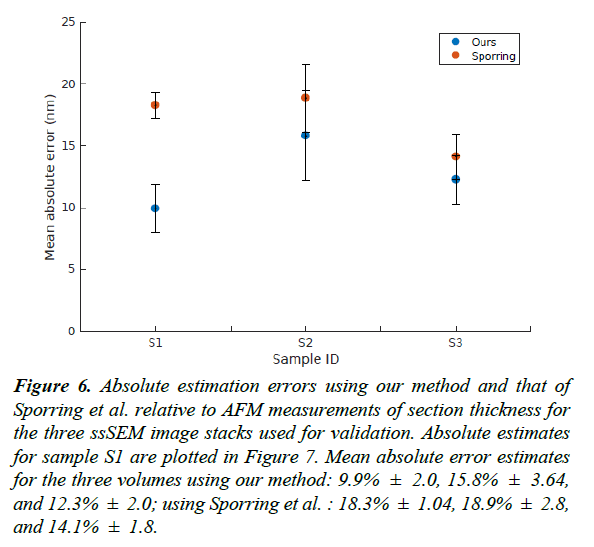
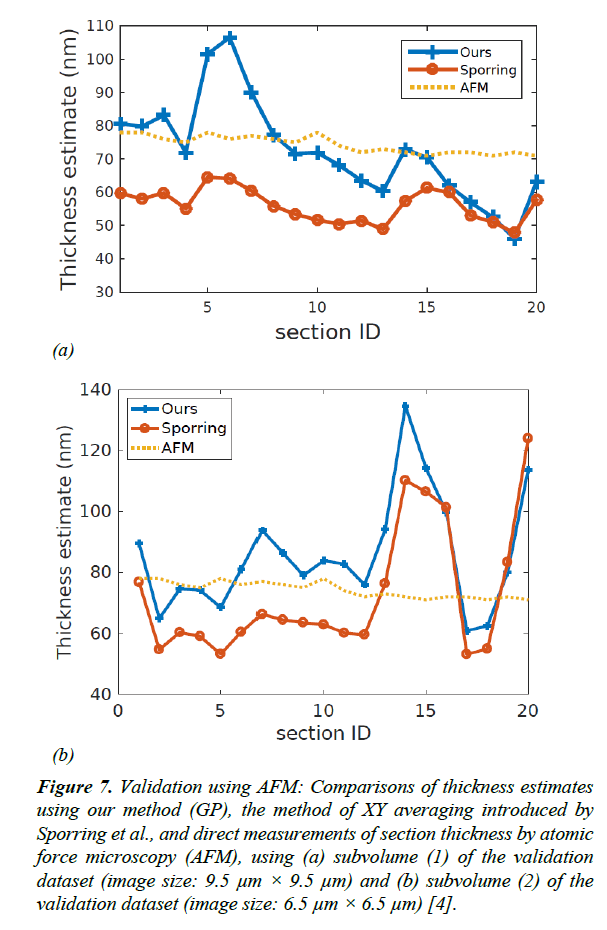
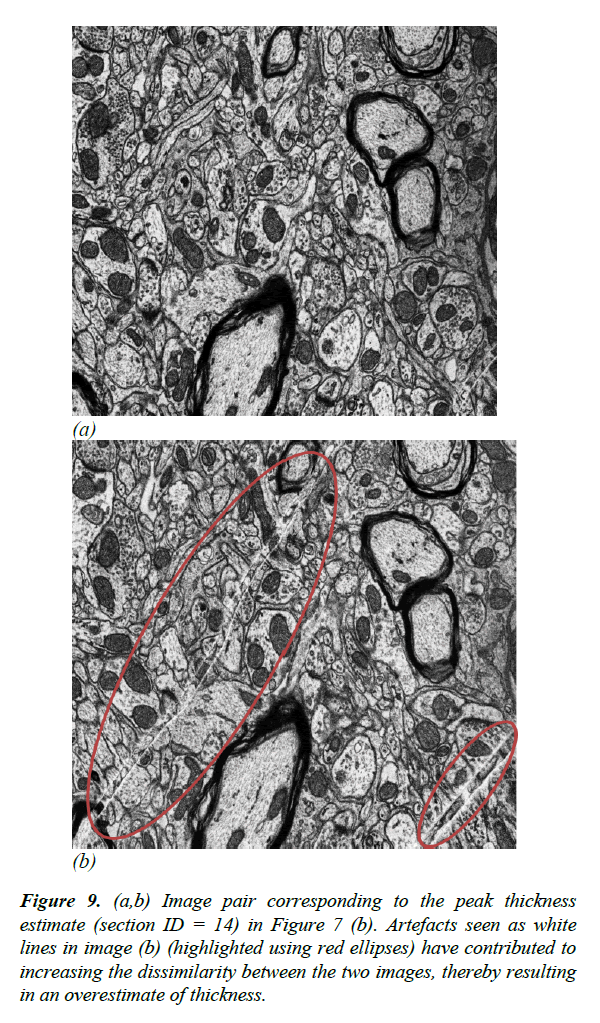
For the validation dataset, the average section thickness measured using AFM was 74.35 ± 2.64 nm. Our method was able to estimate the thickness of the 20 sections with a mean absolute error of 9.91% ± 1.97, whereas the XY-averaging method in Sporring et al. produced thickness estimates with a mean absolute error of 18.26% ± 1.04 [4]. The full comparison of estimation errors is plotted in Figures 6 and 7. Because our estimation method is purely based on image statistics, it is prone to overestimating the thickness when images are noisy. An instance of such an overestimation is illustrated in Figure 9.
Figure 6: Absolute estimation errors using our method and that of Sporring et al. relative to AFM measurements of section thickness for the three ssSEM image stacks used for validation. Absolute estimates for sample S1 are plotted in Figure 7. Mean absolute error estimates for the three volumes using our method: 9.9% ± 2.0, 15.8% ± 3.64, and 12.3% ± 2.0; using Sporring et al. : 18.3% ± 1.04, 18.9% ± 2.8, and 14.1% ± 1.8.
Figure 7: Validation using AFM: Comparisons of thickness estimates using our method (GP), the method of XY averaging introduced by Sporring et al., and direct measurements of section thickness by atomic force microscopy (AFM), using (a) subvolume (1) of the validation dataset (image size: 9.5 μm × 9.5 μm) and (b) subvolume (2) of the validation dataset (image size: 6.5 μm × 6.5 μm) [4].
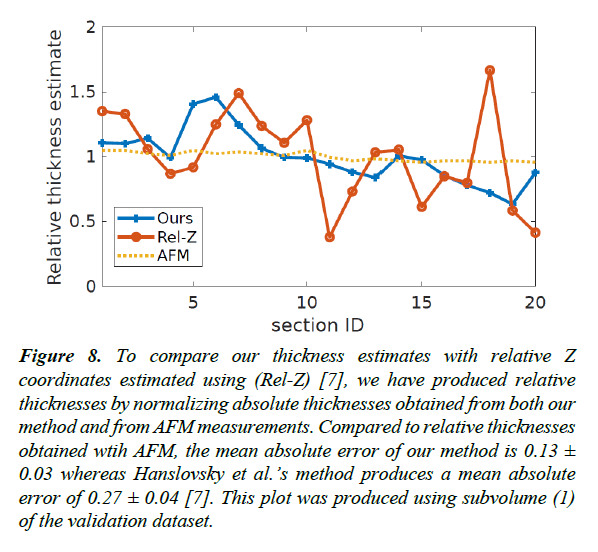
Figure 8: To compare our thickness estimates with relative Z coordinates estimated using (Rel-Z) [7], we have produced relative thicknesses by normalizing absolute thicknesses obtained from both our method and from AFM measurements. Compared to relative thicknesses obtained wtih AFM, the mean absolute error of our method is 0.13 ± 0.03 whereas Hanslovsky et al.’s method produces a mean absolute error of 0.27 ± 0.04 [7]. This plot was produced using subvolume (1) of the validation dataset.
Figure 9: (a,b) Image pair corresponding to the peak thickness estimate (section ID = 14) in Figure 7 (b). Artefacts seen as white lines in image (b) (highlighted using red ellipses) have contributed to increasing the dissimilarity between the two images, thereby resulting in an overestimate of thickness.
Figure 11: Mean thickness estimate (blue line) and standard deviation (Shaded area) as a function of the image size used for thickness estimation. We used 20 images from subvolume (1) of the validation dataset. The arrow points to the image size (7 μm ×7μm) where the average thickness estimate is equal to the average AFM thickness measurement (74.35 ± 2.64 nm the dotted line).
In addition to thickness measurements of ssSEM sections using AFM, we propose a second approach for validating thickness estimates. This second approach uses synthetic sections with known thicknesses derived from nearly isotropic FIBSEM volumes with known XY resolution. We use the method described in the section Estimation of Section Thickness to generate data points for learning the function given in eqn. (2). To validate section thickness estimates, we split each image stack into separate training and test data sets. The training sets were used to learn the regression function given by eqn. (2) and the test images were used for validation. We trained a regression function on 100 images of size 7 μm × 4.5 μm from a FIBSEM image stack, Figure 1. We used the test images to create 3 separate image sequences of 30 images each with known displacements of 10 nm, 50 nm, and 75 nm along the relatively uncompressed axis. The results obtained are summarized in Table 2 along with a comparison with Sporring et al. [4].
Table 2. Average thickness estimates for sets of 30 sections. The “ground truth” thicknesses were derived from nearly isotropic FIBSEM data as described in Section 3.
| Thickness values are in nanometers (nm) | |||
|---|---|---|---|
| “Ground Truth” | 10 | 50 | 75 |
| xy avg. [4] | 9.93 | 47.35 | 69.09 |
| Ours | 10.18 ± 5.61 | 47.02 ± 5.60 | 71.36 ± 5.59 |
Although included for comparison, we note that in Sporring et al. an average distance-dissimilarity curve is generated for each pair of images between which the distance is estimated and therefore the interpolation function is based on the statistics of the validation data itself, unlike in our approach [4]. A recent contribution towards correcting Z coordinates of a 3D image stack is presented in [7,8], where relative Z positions for each image are calculated. In order to compare, we converted absolute thickness estimates of our method and thickness measurements from AFM (subvolume 1 of the validation dataset) into relative thickness by normalizing the thickness values using the mean absolute thickness [7]. With respect to relative thickness values obtained by AFM, our approach resulted in a mean absolute error of 0.13 ± 0.03 where-as, Hanslovsky et al. obtained a mean absolute error of 0.27 ± 0.04 Figure 8 [7]. For this comparison we used the Fiji plugin available for Hanslovsky et al. using its default parameters with the option for reordering disabled [7,22].
Conclusion
We have presented a method for estimating both thickness and stretching in EM imagery, using image statistics alone. Our method is based on learning the distance between adjacent sections as a function of their dissimilarity.
The stretching coefficient quantifies the cumulative effect of different sources of anisotropy along the XY plane including handling, storing, cutting, imaging, and the intrinsic anisotropy of the specimen. Anisotropy estimation is a useful pre-processing step for any method that assumes isotropy in image statistics.
As part of this work, we have created a dataset of 20 ssSEM images along with thickness measurements directly obtained with AFM. We used this dataset to compare the performance of our thickness estimation method with other methods that use image statistics for indirect estimation of section thickness.
Thickness estimation methods based on image statistics alone are prone to be inaccurate if sample anisotropy is not taken into account. We have shown that estimation of XY anisotropy can help to improve the accuracy of thickness estimation. Our anisotropy estimation method selects the optimal rotation of the original image stack to train a regressor that is minimally affected by sample anisotropy. We recommend using images larger than 7 μm × 7 μm so that effects of locally oriented structures may even out given a sufficient scope.
Acknowledgment
We thank Ziqiang Huang, for FIBSEM and ssSEM data, and Thomas Templier for ssSEM data.
References
- Frank J. Electron tomography: methods for three-dimensional visualization of structures in the cell. Springer Science & Business Media. 2008.
- Knott G, Marchman H, Wall D, et al. Serial section scanning electron microscopy of adult brain tissue using focused ion beam milling. Journal of Neuroscience. 2008;28(12):2959-64.
- Funke J, Martel JN, Gerhard S, et al. Candidate sampling for neuron reconstruction from anisotropic electron microscopy volumes. International Conference on Medical Image Computing and Computer-Assisted Intervention. 2014;pp:17-24.
- Sporring J, Khanmohammadi M, Darkner S, et al. Estimating the thickness of ultrathin sections for electron microscopy by image statistics. Biomedical Imaging (ISBI), IEEE 11th International Symposium. 2014;157-60
- https://github.com/thanujadax/ssSEM_AFM_thickness
- https://github.com/thanujadax/gpthickness
- Hanslovsky P, Bogovic JA, Saalfeld S. Post-acquisition image based compensation for thickness variation in microscopy section series. Biomedical Imaging (ISBI), IEEE 12th International Symposium. 2015;507-11.
- Hanslovsky P, Bogovic JA, Saalfeld S. Image-based correction of continuous and discontinuous non-planar axial distortion in serial section microscopy. Bioinformatics. 2017;33(9):1379-86.
- Boergens KM, Denk W. Controlling FIB‐SBEM slice thickness by monitoring the transmitted ion beam. Journal of Microscopy. 2013;252(3):258-62.
- Peachey L. Thin sections: A study of section thickness and physical distortion produced during microtomy. Journal of Biophysical and Biochemical Cytology. 1958;233-42.
- Small JV. Measurement of section thickness. InProc. 4th Eur Conf Electron Microsc. 1968;609-610.
- Fiala JC, Harris KM. Cylindrical diameters method for calibrating section thickness in serial electron microscopy. Journal of Microscopy. 2001;468-72.
- Rasmussen CE, Williams CK. Gaussian processes for machine learning. Cambridge: MIT press. 2006;1.
- Williams CK. Prediction with Gaussian processes: From linear regression to linear prediction and beyond. NATO ASI series. Series D, Behavioural and social sciences. 1998;89:599-621.
- Williams CK, Rasmussen CE. Gaussian processes for regression. Advances in neural information processing systems 1996;8:514-20.
- Binnig G, Quate CF, Gerber C. Atomic force microscope. Physical Review Letters. 1986;56(9):930.
- Bienias M, Gao S, Hasche K, et al. A metrological scanning force microscope used for coating thickness and other topographical measurements. Applied Physics A: Materials Science & Processing. 1998;66:837-42.
- Meli F, Thalmann R. Long-range AFM profiler used for accurate pitch measurements. Measurement Science and Technology. 1998;9(7):1087-92.
- Garnaes J, Kofod N, Kuhle A, et al. Calibration of step heights and roughness measurements with atomic force microscopes. Precision Engineering. 2003;27(1):91-8.
- Challenge IS. Segmentation of neuronal structures in EM stacks. 2012.
- Saalfeld S, Fetter R, Cardona A, et al. Elastic volume reconstruction from series of ultra-thin microscopy sections. Nature methods. 2012;9(7):717-20.
- Schindelin J, Arganda-Carreras I, Frise E, et al. Fiji: an open-source platform for biological-image analysis. Nature methods. 2012;9(7):676-82.