Review Article - Materials Science and Nanotechnology (2018) Volume 2, Issue 1
Unitary relativistic quantum theory.
Eliade Stefanescu*Advanced Studies in Physics Centre of the Romanian Academy, Academy of Romanian Scientists Bucharest, Romania
- Corresponding Author:
- Eliade Stefanescu
Advanced Studies in Physics Centre of the Romanian, Academy
Academy of Romanian Scientists Bucharest, Romania
Tel: +4021-3188106/3138
E-mail: eliadestefanescu@yahoo.fr
Accepted date: February 05, 2018
Citation: Stefanescu E. Unitary relativistic quantum theory. Mater Sci Nanotechnol. 2018;2(1):17-28.
DOI: 10.35841/nanotechnology.2.1.17-28
Visit for more related articles at Materials Science and NanotechnologyAbstract
We consider a quantum particle as a wave packet, and find that the group velocities in the coordinate and momentum spaces are in agreement with the Hamilton equations only when the Lagrangian is considered in the time dependent phases, instead of the Hamiltonian in the conventional forms of these waves as solutions of the Schrödinger equation. We define a relativistic quantum principle, and derive a wave equation for a relativistic quantum particle, the relativistic kinematics and dynamics of the particle waves, the Maxwell equations and the Lorentz force of a field interacting with the particle waves, the relativistic transform of such a field, and the spin as a characteristic of the particle waves. We consider a quantum particle as a distribution of conservative matter propagating according to the General Theory of Relativity. We obtain the dynamics of this matter in a gravitational field, the propagation in plane waves perpendicular to geodesic tracks, and equations of conservation.
Keywords
Quantum particle, Wave packet, Group velocity, Lagrangian, Hamiltonian, Maxwell equations, Spin, metric tensor, Covariant derivation.
Introduction
We perceive the physical world as a collection of objects, in
a three-dimensional space of coordinates defined by a position
vector 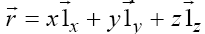 , and in time, defined by a scalar
t [1-5]. For a matter object we define an inertial property called
mass, M0 and a dynamic quantity as the product of the mass
with the velocity,
, and in time, defined by a scalar
t [1-5]. For a matter object we define an inertial property called
mass, M0 and a dynamic quantity as the product of the mass
with the velocity, 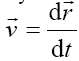 , called momentum,
, called momentum, 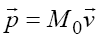 . We
also define a conservative quantity, called energy,
. We
also define a conservative quantity, called energy,
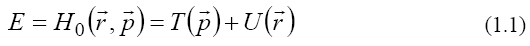
as a sum of the kinetic energy  , which depends on
momentum, and the potential energy
, which depends on
momentum, and the potential energy 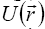 , which depends on
the coordinates [6-8]. From the conservation condition:
, which depends on
the coordinates [6-8]. From the conservation condition:
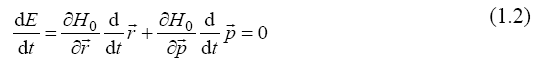
we obtain the dynamic equations called Hamilton equations,
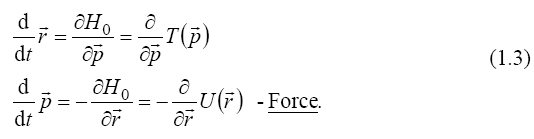
while the energy function of coordinates and momenta,

is called Hamiltonian. However, this classical description
tells us nothing about the structure of the physical world. Only
Quantum Mechanics tells us something about the structure of
this world. Namely, that this world is composed of species of
identical quantum particles. On one hand, experimentally, it has been found that these particles are of a wavy nature. On
the other hand, one could find that the simplest way to define a
quantum particle is by a wave packet, with momenta conjugated
to coordinates and energy conjugated to time, with a single
quantum constant 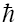 [9-11].
[9-11].
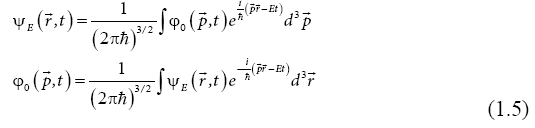
In this case, one can define a momentum operator

and a Hamiltonian operator,
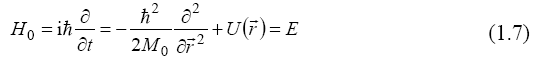
With these operators one obtains eigenvalue equations, for momentum,
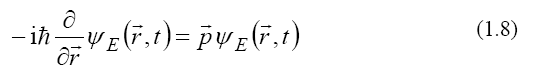
and for energy, as a Schrödinger equation:
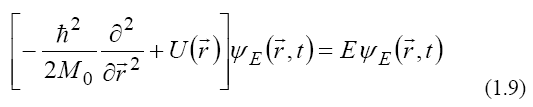
However, when the group velocities are calculated for the wave packets (1.5), which with (1.1) are of the form
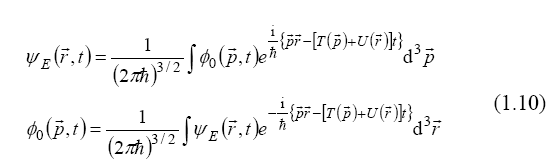
we obtain an erroneous equation, contradictory to the corresponding Hamilton equation (1.3):

- a minus sign is missing [12-14]. We get back the minus
sign only if instead the Hamiltonian 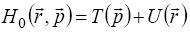 we
consider the Lagrangian
we
consider the Lagrangian
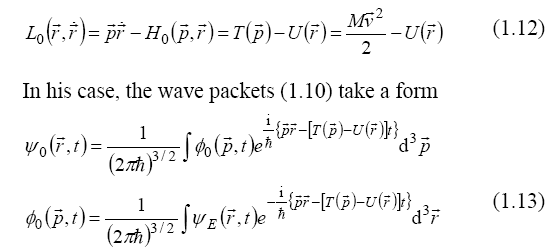
with group velocities in agreement with the Hamilton equations (1.3):
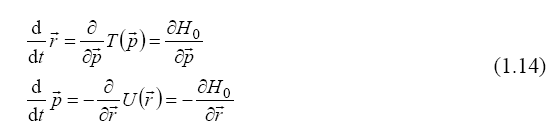
However, this description is still unrealistic, having an infinite spectrum of waves, as a function of the wave velocity 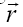 . A finite spectrum is obtained when the relativistic Lagrangian
. A finite spectrum is obtained when the relativistic Lagrangian 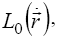
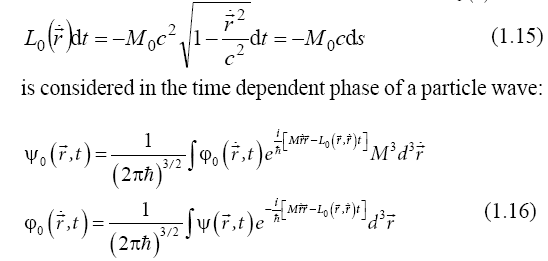
From (1.15), we notice that the invariance of the space- time interval of the Theory of Relativity is equivalent to the invariance of the time dependent phase variation of a quantum particle, and define a Relativistic Quantum Principle: The scalar tim-dependent phase variation of a quantum particle wave is an invariant for an arbitrary change of coordinates. On this basis, in section 2 we obtain the relativistic transform of the space- time coordinates, and the relativistic dynamics of the particle waves. In section 3, we consider a quantum particle in a field described by a scalar potential conjugated to time, and a vector potential conjugated to coordinates. We obtain the Lagrange equation as the velocity of the particle waves, the Lorentz force, and the Maxwell equations. In section 4, based on the Relativistic Quantum Principle, we obtain the dynamics of a quantum particle in electromagnetic field. In section 5, from the invariance of the time dependent phase of a quantum particle at an arbitrary change of coordinates, we obtain the relativistic transform of the electromagnetic field. In section 6, we obtain a relativistic equation for the quantum particle waves, show that the solution of the Schrödinger equation is only the amplitude of the wave function of a quantum particle, which also includes a rapidly varying factor depending on the particle rest mass, and derive the spin of a quantum particle wave. In section 7, we consider the inversion of two particles as a double rotation of these particles, and obtain the spin-statistic relation. In section 8, we consider a coordinate deformation according to the Theory of General Relativity, and obtain the dynamics of the particle waves in gravitational field. In section 9, we consider the particle waves as a distribution of matter described by a density and a velocity field, and find that these waves are perpendicular to the geodesic tracks. We derive an invariant for the matter density of a quantum particle, and an equation of conservation of this matter. Section 10 is for conclusions.
Relativistic Kinematics and Dynamics
A realistic particle has a finite spectrum as a function of the wave propagation velocity. A finite spectrum is obtained for a relativistic Lagrangian. According to (1.15), the invariance of the scalar time dependent phase variation 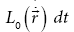 of a quantum particle wave
function is equivalent to the invariance of the space-time interval
ds. For such a particle, we obtain the momentum,
of a quantum particle wave
function is equivalent to the invariance of the space-time interval
ds. For such a particle, we obtain the momentum,
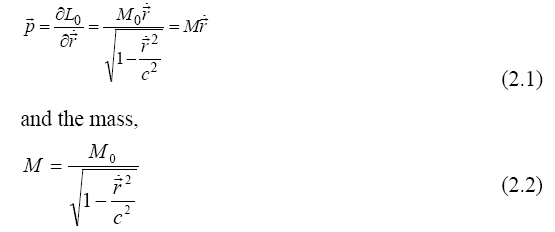
as functions of the particle velocity 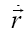 and the cut-off
velocity c. The invariance of the space-time interval means that
a change of coordinates is in fact a rotation of the space-time
coordinates (Figure 1).
and the cut-off
velocity c. The invariance of the space-time interval means that
a change of coordinates is in fact a rotation of the space-time
coordinates (Figure 1).
By a well-known calculation, the relativistic transform of the coordinate intervals is obtained for the quantum particle waves. Thus, from the coordinate transform,
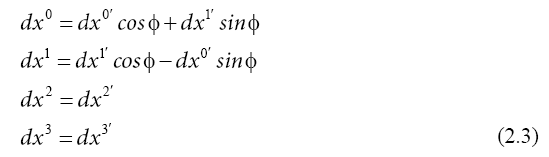
with the expressions of the rotation angle trigonometric functions,
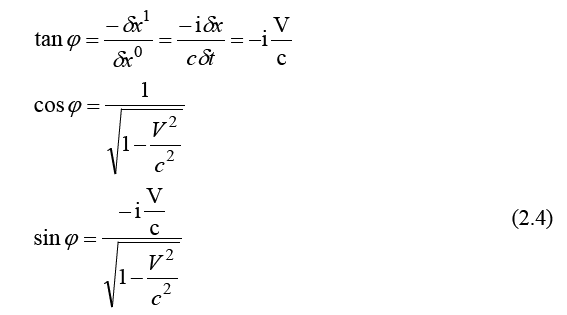
for the coordinates of a quantum particle wave, we obtain the transform:
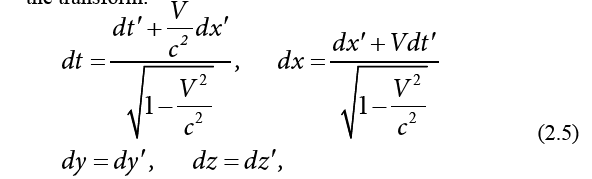
which, in this case does not refer to the coordinates of some classical particle as in the conventional Theory of Relativity, but to the coordinates of the quantum particle waves.
Electromagnetic Field
When a particle with a charge e is placed in a field of a vector
potential 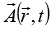 conjugated to the coordinates, and a scalar
potential
conjugated to the coordinates, and a scalar
potential 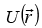 conjugated to time, for the two wave packets of
this particle
conjugated to time, for the two wave packets of
this particle
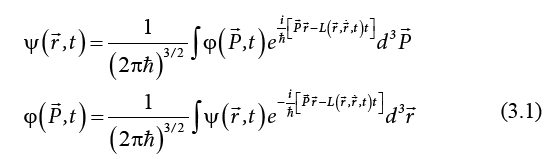
a time dependent phase variation arises, with terms proportional to the coordinate variations, and the time variation,
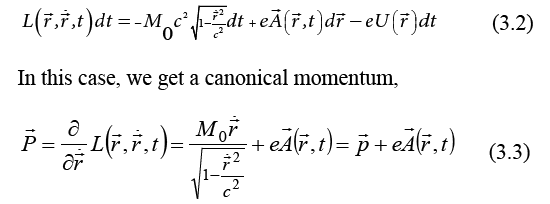
with a mechanical component depending on the particle mass and velocity, and an electromagnetic component as the product of the particle charge with the vector potential. For a quantum particle in a field we consider again the relativistic quantum principle: The time dependent phase variation of a quantum particle is the same in any system of coordinates.
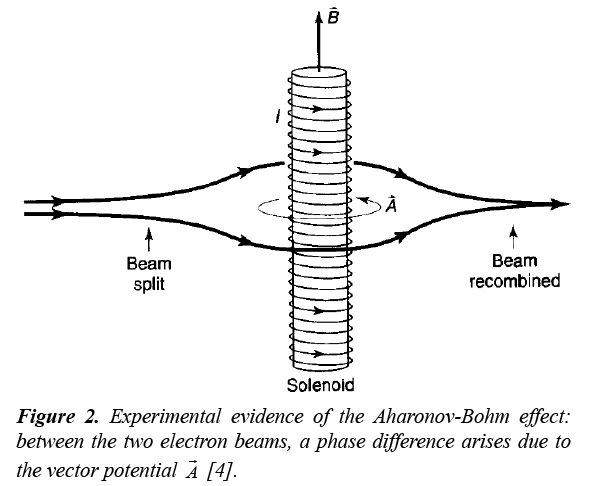
We are in agreement with the Aharonov-Bohm effect [15]:
the time-dependent phase of a quantum particle 
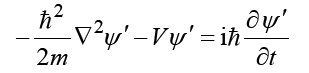
in a magnetic field includes a term proportional to the space integral of the vector potential of this field:
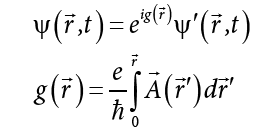
This effect has been experimentally put out into evidence (Figure 2).
Figure 2: Experimental evidence of the Aharonov-Bohm effect:
between the two electron beams, a phase difference arises due to
the vector potential  [4].
[4].
Besides this variation, we consider a time-dependent phase variation with a term proportional to the scalar potential and time, and the invariance of this phase. From equation (3.3), we obtain the electric force:
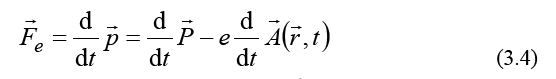
while from a particle wave velocity in the momentum space we obtain the Lagrange equation:

Taking into account that the curl of the gradient is null, from (3.8) with (3.9) we obtain the Faraday-Maxwell law of the electromagnetic induction:
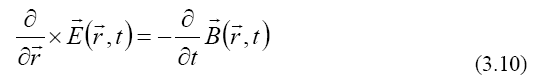
Taking into account that the divergence of the curl is null, from (3.9) we obtain the Gauss-Maxwell law for the magnetic induction flow:

With the Gauge condition

we obtain the Gauss-Maxwell law for the electric field flow:
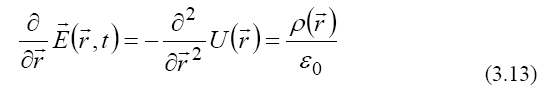
with the Laplacian of the scalar potential as source of this
divergence, considered as a ratio of the charge density 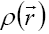 and the dimensional constant ε0 called electric permittivity.
Considering a current density under the action of the electric
field,
and the dimensional constant ε0 called electric permittivity.
Considering a current density under the action of the electric
field,
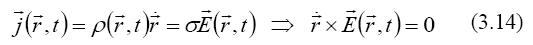
with the vector formula
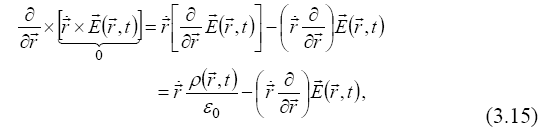
we obtain the time derivative of the electric field of the form:
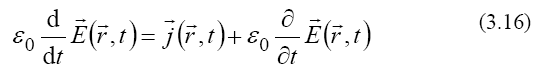
For the relation (3.10) of the two vector fields, asserting that a time variation of a magnetic field determines a curl of the electric field, we consider a symmetric relation, namely that a time variation of the electric field determines a curl of the magnetic field:
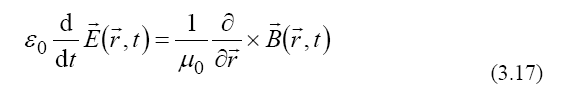
From (3.16) and (3.17), the Ampère-Maxwell law of the magnetic circuit is obtained. In this way we obtain the whole system of Maxwell equations:
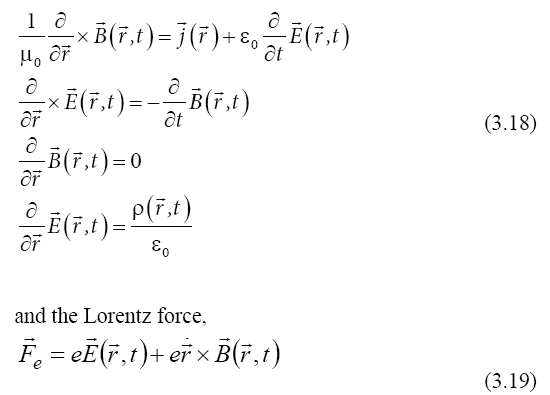
This force acts on the particle wave functions (3.1), with the time-dependent phase coefficient:
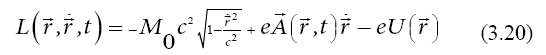
as a function of the two potentials of the electromagnetic field:
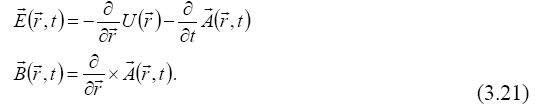
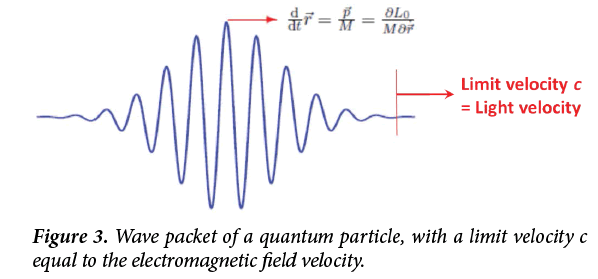
It is interesting that by the hypothetical relation (3.17), we
obtain a field propagating in waves with a velocity 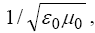 in agreement with the electromagnetic theory. For the physical
consistency, this velocity takes the limit value of the velocity of
the quantum particle waves (Figure 3):
in agreement with the electromagnetic theory. For the physical
consistency, this velocity takes the limit value of the velocity of
the quantum particle waves (Figure 3):

Otherwise, an electromagnetic field not interacting with a quantum particle, or a quantum particle not interacting with any electromagnetic field could exist, which is contradictory to our basic hypothesis of the particle-field interaction.
Dynamics of a Quantum Particle in Electromagnetic Field
We consider the space-time interval,

and the phase variation (3.2),
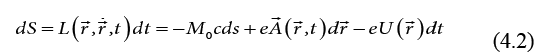
as functions of the coordinate four-vector

and the field four-vector
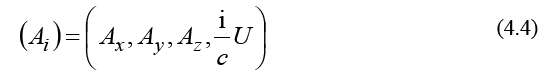
For the wave velocity in the space of the momentum (3.3), from (3.1) we obtain a wave/group velocity of the form of the Lagrange equation:
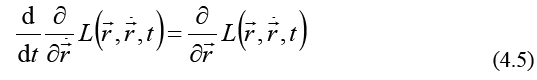
which means that the time-dependent phase of a quantum particle wave function is of the form of the action of the Lagrangian (3.20),


for the interaction of a particle wave with an electromagnetic field.
Relativistic Transform of a Field Interacting with a Quantum Particle
For a coordinate four-vector transform,
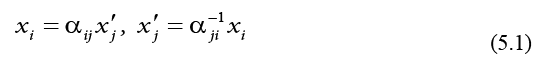
with the transformation matrix,
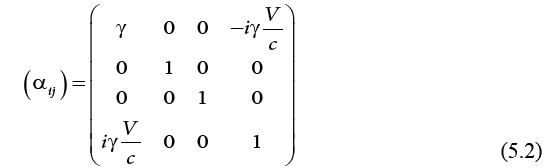
in the least action equation (4.7), we obtain an invariant including a mechanical term and an electromagnetic term:
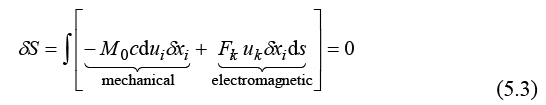
Since the mechanical term is invariant to any change of coordinates,
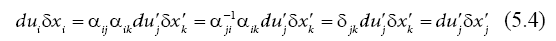
the electromagnetic term must be also an invariant,
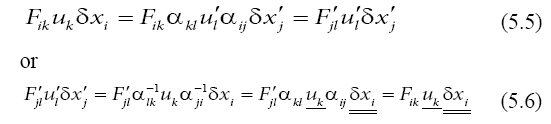
On this basis, we find the transform for a change of coordinates of a field interacting with a quantum particle
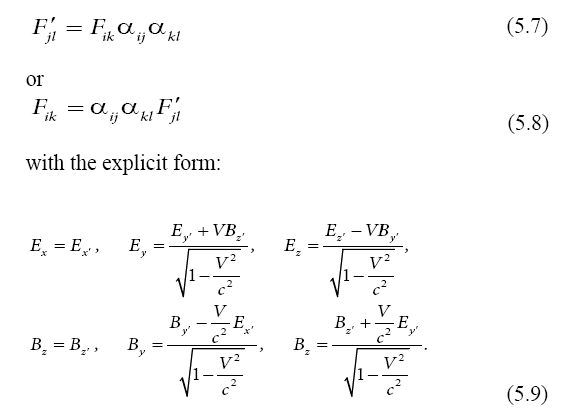
Particle Wave Function and Spin
From the Lagrange equation obtained as the group velocity (3.5) with the momentum expression (3.3),
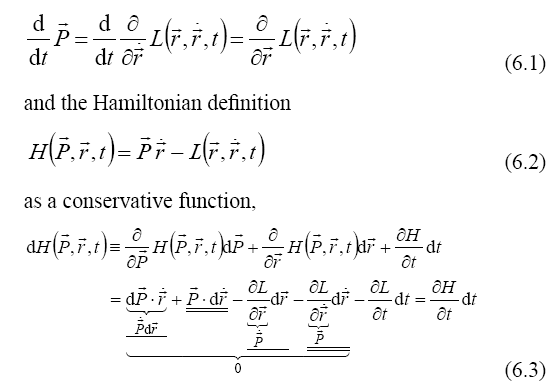
we obtain the Hamilton equation
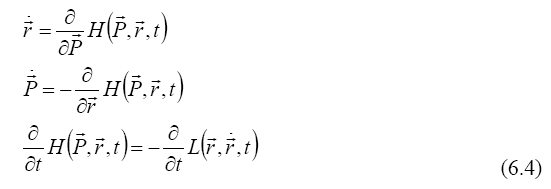
At the same time, with the definition expression (6.2), the wave packets (3.1) take a form
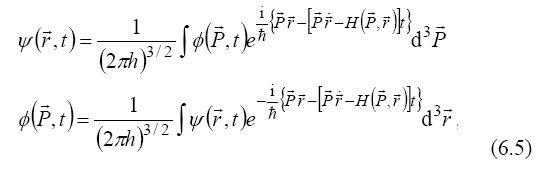
as solutions of a wave equation

which, compared to the Schrödinger equation includes a term depending on the velocity.
On the other hand, from (3.1) we notice that, in a classical approximation,
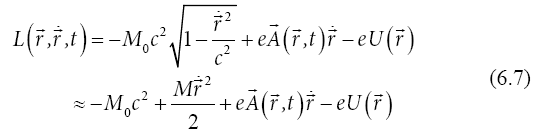
the Schrödinger wave function 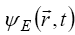 , we usually use in
our studies, in fact is not the particle wave function, bat only an
amplitude of a wave function including a rapidly varying factor,
, we usually use in
our studies, in fact is not the particle wave function, bat only an
amplitude of a wave function including a rapidly varying factor,

We consider an electromagnetic field with a constant scalar
potential for a stationary electric field, and a time-dependent
vector potential for a coherent radiation field. From equation
(6.2) with (3.3) and (3.20), we notice that although the vector
potential 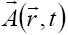 depends on time, the Hamiltonian does not:
depends on time, the Hamiltonian does not:
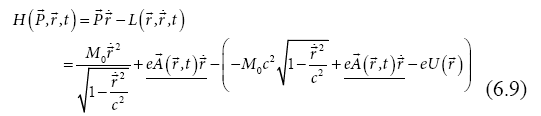
With this Hamiltonian we, obtain the total energy as a function of the mechanical energy and the potential energy in electric field:
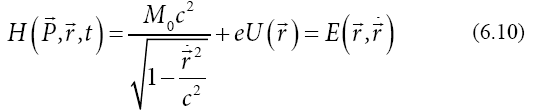
With the mechanical energy as a function of the canonical momentum (3.3),

we obtain the canonical form of the Hamiltonian
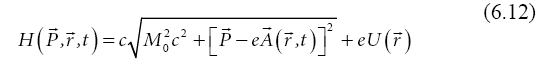
According to Dirac’s well-known spin theory, we consider the Schrödinger equation
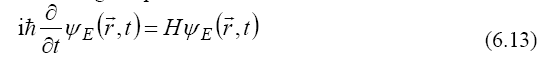
with the Hamiltonian
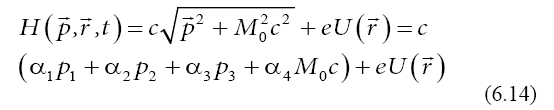
which depends on Dirac’s spin operators
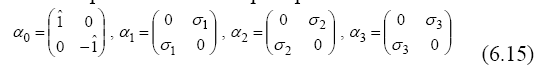
as functions of Pauli’s spin operators,
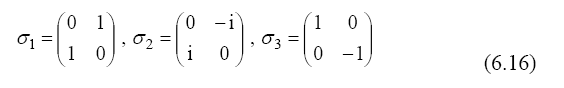
These operators satisfy the commutation relations:
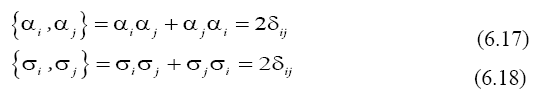
With the notation

the Schrödinger equation (6.13) with the Hamiltonian (6.14) takes a form:
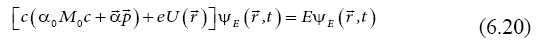
with a wave function which can be written as a vector with two components, or a vector with four components,

We obtain the two-dimensional Schrödinger-Dirac equation,
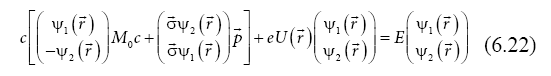
with two coupled Schrödinger-Dirac equations for the two
components  and
and 
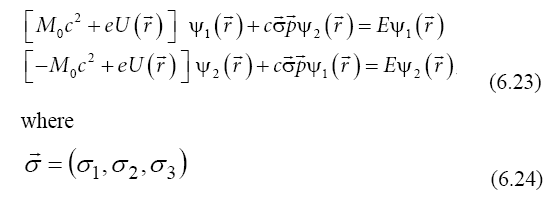
By eliminating the coupling terms, the two Schrödinger- Dirac equations take non-linear forms, which, in a non- relativistic approximation, small velocity, small electric potential, become linear:
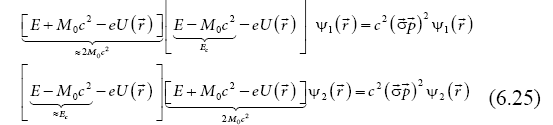
In the non-relativistic approximation, we get Schrödinger- Dirac equations
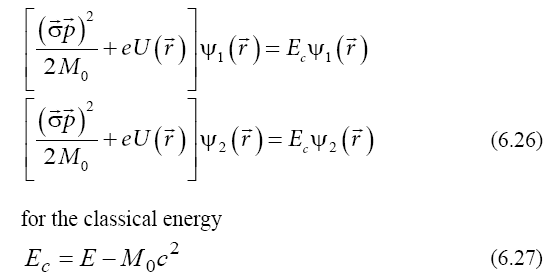
The Hamiltonian of these equations includes a kinetic term depending on the momentum and the Pauli spin operators,
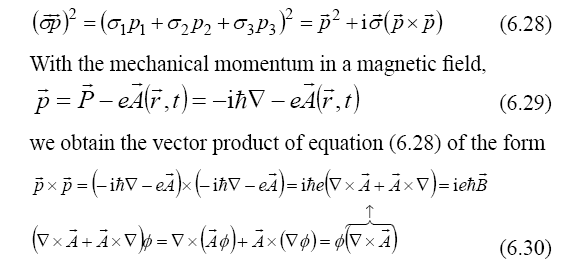
Thus, in the kinetic term of the Hamiltonian, besides the mechanical term, proportional to the square of the mechanical momentum, we obtain a magnetic potential, proportional to the magnetic field, as of a proper rotation, called spin:

We obtain Schrödinger-Dirac equations with a Hamiltonian including the kinetic energy, the electric potential energy, and a potential energy in magnetic field, due to the particle spin:
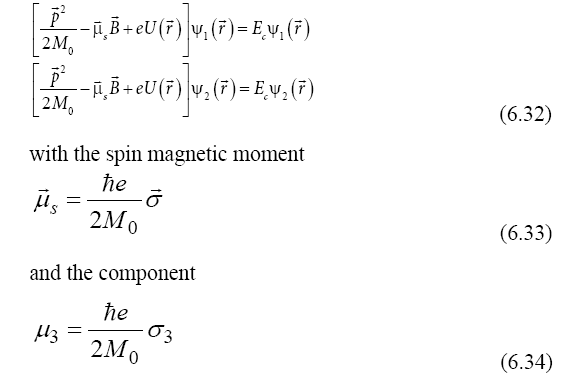
in the direction of the magnetic field. Taking into account the commutation relation
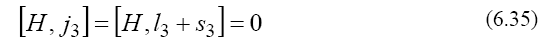
of the Hamiltonian

with the total angular momentum, which includes the orbital angular momentum l3 and the spin angular momentum s3, we obtain a relation between the spin angular momentum and the orbital angular momentum which is known:
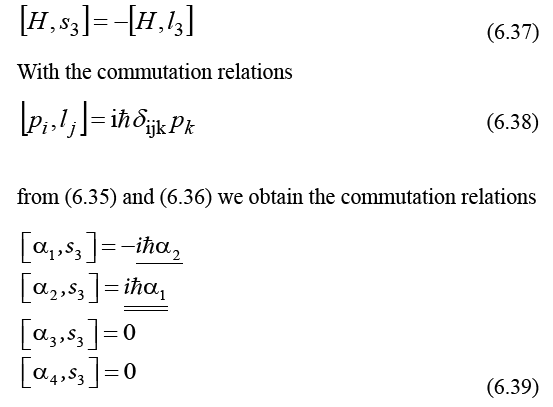
These equations have a solution of the form
s3 = sα1α2 (6.40)
with the coefficient

Thus, we obtain the spin angular momentum in the direction of the magnetic field
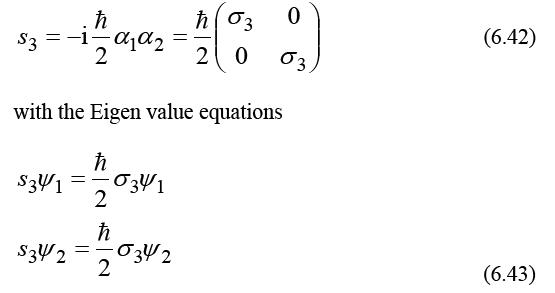
From (6.34) and (6.41) we obtain the gyromagnetic ratio

In this way, the spin is obtained from the relativistic quantum principle, in the framework of a unitary relativistic quantum theory.
Spin-Statistic Relation
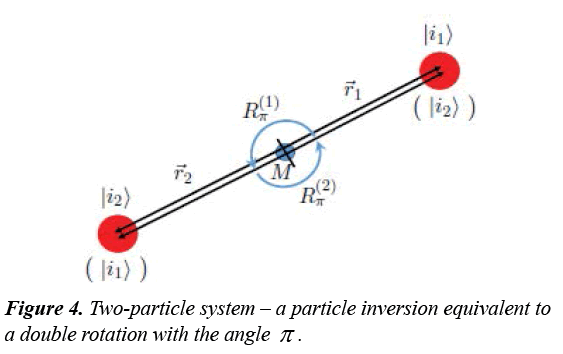
We consider a system of two particles, in the states 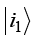 and
and 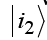 , with the position vectors
, with the position vectors 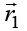 and
and 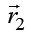 (Figure 4).
(Figure 4).
For a two particle wave function

On the other hand, we notice that an inversion is equivalent with a double rotation with the angle π (Figure 4),

For a wave function rotation with a differential angle 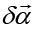 ,
,
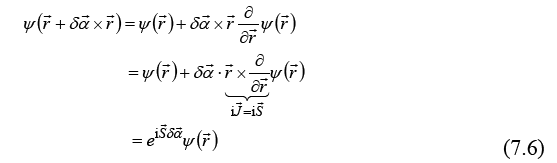
we find a rotation operator depending on the spin operator 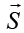 ,
,

which, for a rotation with an arbitrary angle 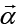 generates
generates 
For α =π we obtain

With this expression, from (7.4) and (7.5) we obtain the inversion eigenvalues as a function of spin,
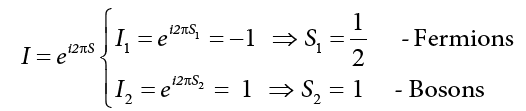
Quantum Particle in Gravitational Field
We consider the wave functions (1.16) in a system of
curvilinear coordinates 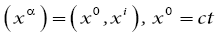 ,
,
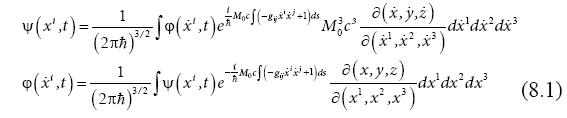
with the time-space differential interval ds,

and use Dirac’s formalism of General Theory of Relativity [16]. In (8.1), we used the notation:
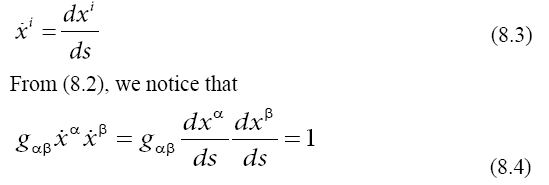
For a non-relativistic case, small particles compared with the non-uniformities of any gravitational field, small velocities, we consider:
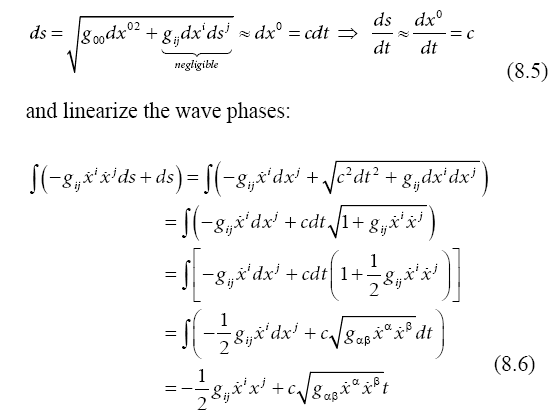
In this way, for a quantum particle we obtain wave packets with linear phases in space and time,
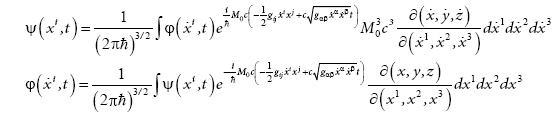
For this wave packet we obtain a self-consistent expression of the wave velocity,
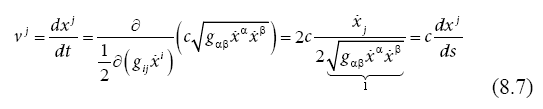
and the acceleration of a particle on a geodesic as a function
of the Christoffel symbol 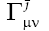 of the second kind,
of the second kind,
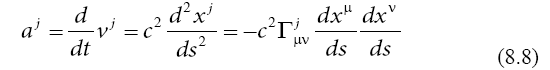
We introduce the Christoffel symbol of the first kind, and consider the expression of this symbol as a function of the metric tensor derivatives:
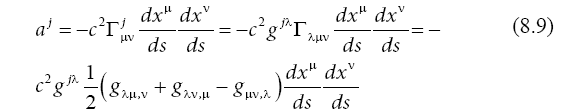
For the non-relativistic case, considered here, we neglect the spatial coordinate derivatives compared to the time derivative, and take into account a stationary state, which means that the derivatives with time disappear. We obtain a particle accelerations proportional to the derivatives of the metric tensor element g00:
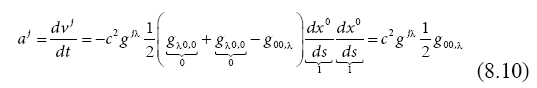
which means that this matrix element behaves as a potential. Considering the Newtonian potential V in this matric element,
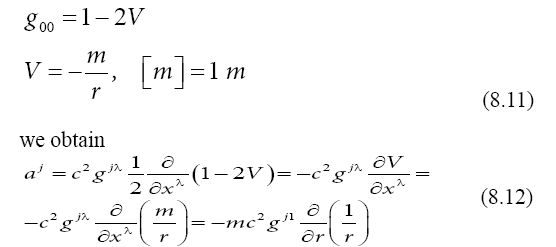
With the Schwarzschild solution for the contravariant metric elements conjugated to the spatial coordinates, we obtain the three components of the acceleration,

We notice that, for a rather small distance r, we obtain a correction of the Newtonian force, increasing the gravitational attraction.
Quantum Particle as a Distribution of Matter
We notice that, in this framework, a particle is conceived as a distribution of matter with a matter velocity field:
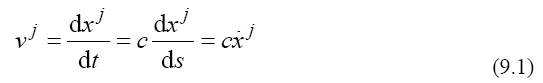
From the relativistic quantum principle of the space-time interval invariance,

we obtain that the covariant derivative of velocity vector is perpendicular to this vector,
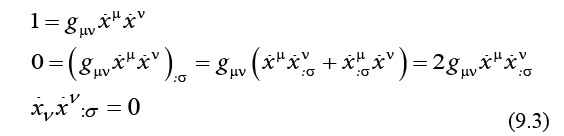
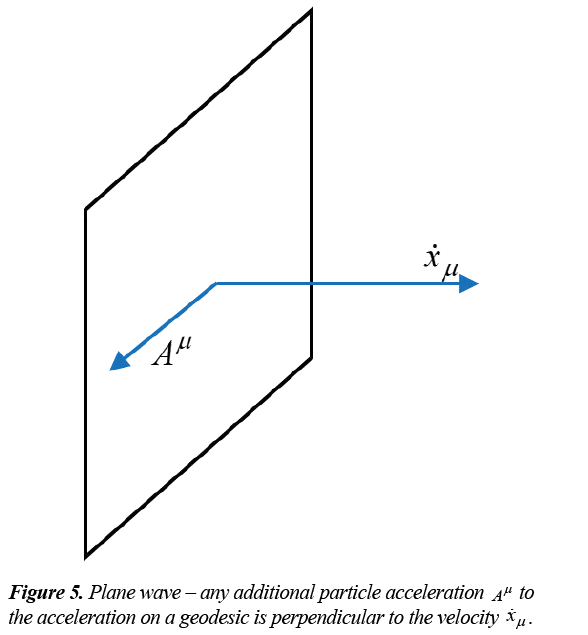
If, besides the acceleration on a geodesic track, we consider
an additional component 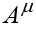 ,
,
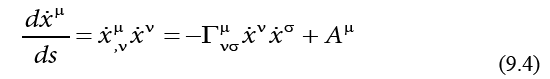
we find that this component is perpendicular to the velocity vector:
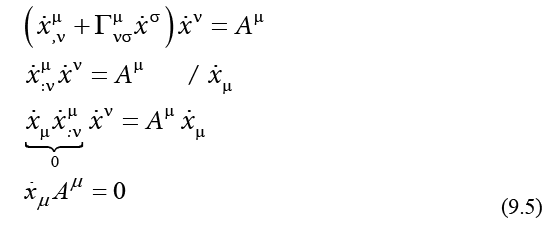
This means that any additional acceleration to the acceleration on a geodesic is perpendicular to the wave velocity, which is in agreement with wave propagation (Figure 5).
In particle propagation on a geodesic, other matter propagations are allowed only in perpendicular directions on the particle velocity.
We consider a quantum particle as a normalized matter distribution – a normalized integral of the matter density, in Cartesian coordinates,
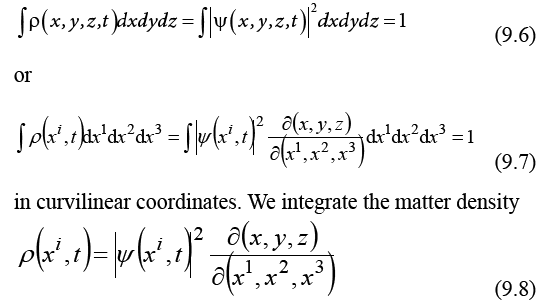
on a space-time volume  , in two systems of coordinates.
, in two systems of coordinates.
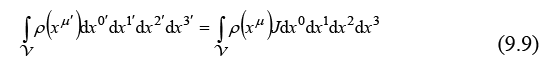
and remark that the elements of the Jacobian,
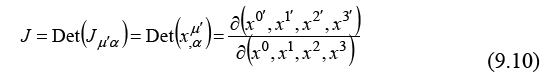
are also elements of a tensor transform, which, for the metric tensor is:

Calculating the determinants,

we obtain the Jacobian as a function of the determinants of the metric tensor in the two systems of coordinates,

Introducing this expression of the Jacobian in the integral equation (9.9), we obtain an invariant for the matter density:

We consider a matter flow density  , as the product
of the matter density with the velocity
, as the product
of the matter density with the velocity

and the matter conservation as a null covariant divergence
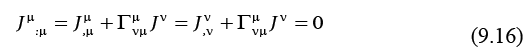
From the general expression of the Christoffel symbol of the second kind as a function of the metric tensor,
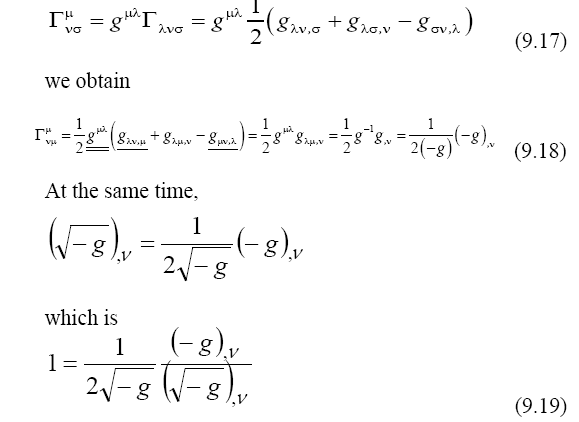
From (9.18) and (9.19), we obtain the Christoffel symbol of the second kind in the expression (9.16),

which takes the form of a divergence of the product of the matter flow density with the square root of the metric determinant,
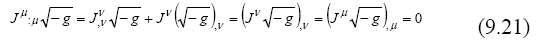
Integrating this expression on a volume V of spatial coordinates,
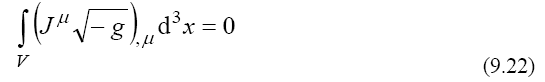
and separating the time derivative from the coordinate derivatives, we find a conservation law, as a matter variation in a volume V by the flow of this matter through the surface ΣV of the volume V:
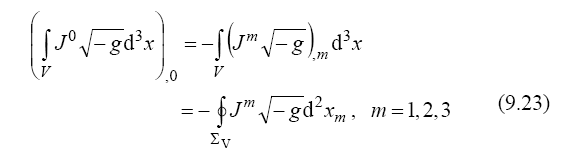
In the nonrelativistic case, 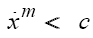 , weak gravitational
field, we obtain
, weak gravitational
field, we obtain

while the conservation equation (9.23) takes a more explicit form, of density and matter flow,

Conclusion
We discovered that a packet of Schrödinger wave functions, representing a quantum particle, is not in agreement with the Hamilton equations which describe the dynamics of such a particles – such an agreement is obtained only when instead of the Hamiltonian we consider the Lagrangian function. For a realistic particle, which must have a finite spectrum, we considered the relativistic Lagrangian, with a cut-off velocity c. We defined a Relativistic Quantum Principle: The time-dependent phase of a quantum particle is invariant to any change of coordinates. We obtained a wave equation for a quantum particle, depending on velocity, while the conventional Schrödinger equation describes only the amplitude of the particle wave-function - it includes a rapidly varying factor, with a phase proportional to the particle rest mass. On this basis, the relativistic kinematics and dynamics, the electromagnetic field equations, the particle spin, and the Schwarzschild-Newtonian dynamics in a gravitational field have been obtained. A quantum particle has been described by a wave function representing a distribution of conservative matter in motion, according to the General Theory of Relativity.
References
- Brody T. The philosophy behind physics. Berlin and Heidelberg: Springer-Verlag. 1993.
- Rowlands P. The foundations of physical law. New Jersey, London, Singapore, Beijing, Shanghai, Hong Kong, Taipei and Chennai: World Scientific. 2015.
- Barret R, Delsanto PP, Tartaglia A. Physics: The ultimate adventure. Springer. 2016.
- Cox B, Forshaw J. The quantum universe. Boston: Da Capo Press. 2012.
- Penrose R. The road to reality. London: Vintage Books. 2004.
- Hall MJW, Reginatto M. Ensembles on configuration space - Classical, quantum and beyond. In Fundamental Theories of Physics. Springer. 2016;184.
- Feynman RP, Leighton RB, Sands M. The Feynman lectures on physics. Reading, Massachusetts: Addison-Wesley. 1963.
- Landau L, Lifchitz E. Théorie du Champ. Moscou: Edition Mir. 1966.
- Broglie L. Théorie de la quantification dans la nouvelle Mécanique. Paris: Hermann et Cie. 1932.
- Heisenberg W. The physical principles of the quantum theory. New York: Dover Publications. 1949.
- Pagels HR. The cosmic code - Quantum physics as the language of nature. Toronto, New York, London, Sydney: Bantam Books. 1983.
- Stefanescu E. The relativistic dynamics as a quantum effect. J Basic Appl Res Int. 2014:1(1);13-23.
- Stefanescu E. Open quantum physics and environmental heat conversion into usable energy. Sharjah (UAE), Brussels and Danvers (Massachusetts, USA): Bentham Science Publishers. 2014.
- Stefanescu E. Open quantum physics and environmental heat conversion into usable energy. Sharjah, U.A.E.: Bentham Science Publishers. 2017.
- Kregar A. Aharonov-Bohm effect. University of Ljubljana. Faculty of Mathematics and Physics. Department of Physics. Seminar 4. Ljubljana. 2011.
- Dirac PAM. General theory of relativity. New York, London, Sydney and Toronto: John Wiley & Sons. 1975.
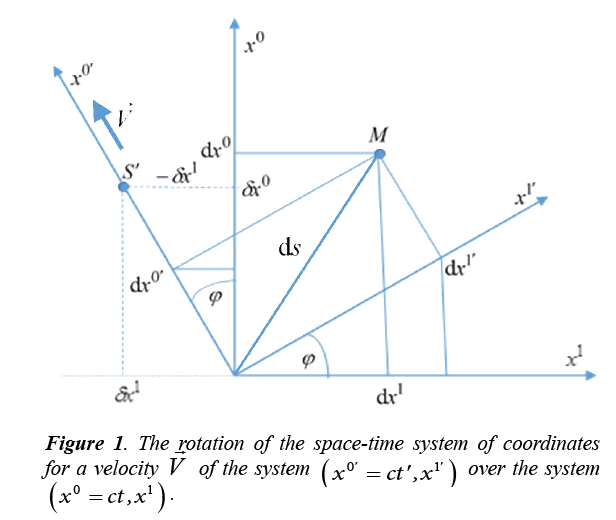
 of the system
of the system 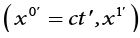 over the system
over the system 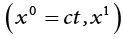 .
.