Review Article - Journal of Cancer Immunology & Therapy (2018) Volume 1, Issue 1

Modelling approaches in tumor microenvironment.

Isaac Crespo^1*, George Coukos², Marie-Agnès Doucey² and Ioannis Xenarios^1*

¹Vital-IT, SIB (Swiss Institute of Bioinformatics), University of Lausanne, Switzerland

²Ludwig Center for Cancer Research, University of Lausanne, Switzerland

*Corresponding Authors:

Ioannis Xenarios
Vital-IT, SIB (Swiss Institute of Bioinformatics)
University of Lausanne, Switzerland
E-mail: lioannis.xenarios@isb-sib.ch

 

Isaac Crespo
Vital-IT, SIB (Swiss Institute of Bioinformatics)
University of Lausanne Switzerland
E-mail: isaac.crespo@isb-sib.ch

Accepted date: 30 January 2018

Citation: Crespo I, Coukos G, Doucey M, et al. Modelling approaches to discovery in the tumor microenvironment. J Cancer Immunol Ther. 2018;1(1):26-40.

Abstract

For decades, cancer research has been focused on understanding the neoplastic transformation of normal cells into cancerous ones from a cell-centric perspective. However, it is increasingly evident that the surrounding tumor microenvironment (TME) is equally important for tumor growth, progression and dissemination. The TME is a complex and heterogeneous system of interplaying elements strongly intertwined with normal processes of the surrounding hosting tissue. Cancerous cells and stromal cells, including different types of infiltrating immune cells and resident tissue cells, interact with each other and with extracellular matrix components in a very convoluted way. In addition, all of these cells may have phenotypically distinct variants exhibiting variability in cell traits, such as cell-cell adhesion, migration capability, proliferation rate and responsiveness to specific treatments; the composition of the cell population can differ between different regions of the tumor and between different tumors of the same or different patients, which result in both intratumor and across tumor heterogeneity. Altogether, the complexity and heterogeneity of the TME hinder the elucidation of cancer driving mechanisms and biomarkers and render the tumor behavior difficult to anticipate. Ultimately, that slows down the development of novel cancer therapies and makes difficult the choice of suitable treatments for specific patients. Mathematical and computational models may help on describing, explaining and predicting cancer in a new generation of experimental design assisted by computer simulations. These novel experimental and computational approaches face new challenges in the era of precision medicine and personalized cancer therapies, such as capturing the spatiotemporal structure of the TME, vertical and horizontal integration of multiple-omics data and dealing with heterogeneity at both intratumor and patient population level.

Keywords

Tumor micro-environment, Tumor-infiltrating lymphocytes, Ordinary differential equation, Petri net, Boolean networks, Linear programming, Agent-based model, Metalloproteinases, Non-small cell lung carcinoma

Introduction

TME complexity and heterogeneity

Nowadays, TME is frequently referred as a complex system [1]. Despite, there is no consensus on what a complex system means [2], there are at least two commonly accepted features that arguably apply to TME: 1) It is inherently complicate and intricate; there are a number of constituent elements, with multiple interactions between them; 2) Its evolution is very sensitive to initial conditions or to small perturbations [3]. Both features render the TME and its dynamic behavior intrinsically difficult to model and anticipate.

In addition to its inherent complexity, the diverse constituent elements of the TME, such as cancer and stromal cells, exist in phenotypically distinct variants with variability in cell traits, such as cell-cell adhesion, migration capability, proliferation rate and responsiveness to specific treatments. The proportion of different cell types and variants may change across different regions of a solid tumor, effect that is commonly referred as intratumoral heterogeneity. In addition, there may be differences across tumors from the same or different patients, which is referred as intertumoral heterogeneity.

Moreover, the internal TME structure or compartmentalization has to be taken into account. For example, from the histological point of view, tumors can be roughly classified in inflammed or noninflamed [4]. The main feature of inflamed tumors is the presence of tumor-infiltrating lymphocytes (TIL), in particular IFNγ-producing and PD-L1 expressing CD8+ T cells, whereas noninflamed tumors are poorly infiltrated by TIL. The formers usually exhibit high mutational burden and a preexisting antitumor response, whereas the latters are characterized by the lack of this response and for being highly proliferative tumors with low mutational burden.

Clinical evidences support that checkpoint inhibitors mainly act by reinforcing a previously existing antitumor response and are much more effective in inflamed tumors [5,6]. However, the precise location of TIL is critical, as there exist some tumors with TIL confined to the periphery (excluded infiltrate), which do not respond to checkpoint inhibitors. Consequently, both biological and computational models should capture the internal architecture of the TME; the total count of TIL is not meaningful unless we consider also the spatial distribution. Furthermore, the temporal distribution of interacting elements of the TME is also relevant, as, for example, infiltrating TIL may differ in number at time of diagnosis and during treatment; only TME elements that coincide in space and time can interact.

Both cellular counts and spatiotemporal distribution of TIL, tumor cells, and other stromal cells can affect the way they interact with each other in the TME, which in turn can impact cell functions and response to treatments.

At the experimental level, it is essential to preserve the global architecture of the TME in order to capture the tumor heterogeneity and complexity [7]; most of the current studies that employ cell lines or simplified co-cultures are very limited in their ability to predict the clinical outcome of treatment with accuracy, as they mainly rely on cancer-cell biomarker-based approaches [8]. However, a suitable biological model or experimental platform of the TME can be tested in many different ways; an exhaustive perturbation of all of its constituent elements and potential intervention points by trial and error under all possible experimental conditions become rapidly unaffordable. There is need for computational models and simulations to prioritize some tests and discard others in an assisted experimental design in order to render these platforms cost effective. As complex systems are predisposed to unexpected outcomes due to the so-called emergent behavior, it is unlikely that predicting a response to specific treatments based on the analysis of the individual components of the TME is possible. Alternatively, in a more holistic spirit, global integrative models considering different cell types and scales of complexity and including not only cancer driving but also treatment response mechanisms are more likely to be able to

Types of models used in cancer research: probabilistic vs. deterministic

Computational models can be roughly classified into probabilistic and deterministic, depending on how rigid the underlying mechanisms are assumed, or, in other words, how certain cause-effect relationships are within the model.

In general, in probabilistic model’s specific events may or may not take place with a given probability, so there is certain randomness involved, whereas in deterministic models, biological processes are described by mean of equations that always produce the same output for a given starting conditions. Both modeling approaches have been pervasively used in cancer research to describe cancer related processes in both unperturbed (untreated) and perturbed (treated) TME.

It is worth noting here that, despite the stochastic nature of its constituent elements, as a whole the evolution of a complex biological system in response to perturbation can be more reproducible and predictable than expected, responding in most of the cases in a consistent manner. This is the case, for example, of the immune response to eliminate pathogens without severe harm of normal tissue; paradoxically, the randomness and stochastic behavior at the lower level of the immune system (single cell level) is integrated to derive a more predictable outcome at the system level (local or systemic immune response), resulting, for example, in a controlled variability of the T cell activation [8], or a predictable course of lymphocyte expansion and contraction after exposure to a pathogen in spite of the intrinsic randomness in individual cell fate [9,10].

Thus, despite the behavior of the TME is more likely to be the probabilistic output of a complex and stochastic system [11], it can be also conceptualized, in a deterministic or mechanistic manner, as a collection of cellular mechanisms and signaling pathways that always have the same behavior under the same circumstances. That allows a wide range of modeling formalisms from purely probabilistic to purely deterministic in order to describe, explain, simulate and predict cancer related events in the unperturbed TME (in the absence of any treatment) and in response to therapy (See table 1).

Table 1: Modeling formalisms and model construction strategies commonly used in cancer research.

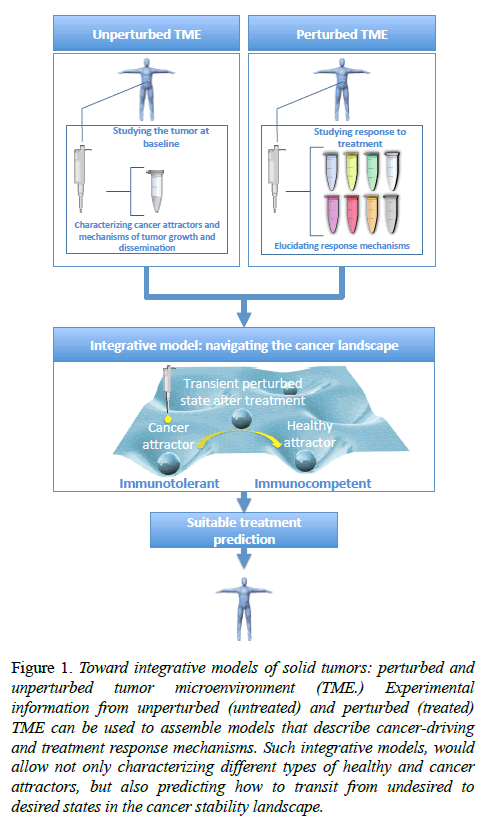
Cancer landscape: unperturbed vs. perturbed TME

Models can be focused on specific parts or processes of the TME in a classical reductionist (top-down) approach or try to capture the emergent properties of the system as a whole in a more holistic spirit (bottom-up), which refer to the ideas of "divide and conquer", and "the whole is more than the sum of its parts", respectively. The former corresponds to a more classical research strategy, whereas the latter refers to the systems biology paradigm. Resulting from this systems or holistic view of solid tumors, some properties arise with potential prognostic and therapeutic interest. Particularly interesting are the concepts of the cancer stability landscape and cancer attractors [22], or self-maintained cancer programs derived from the stability of the underlying regulatory network. The implicit assumption is that, due to both the intrinsic features of stromal cells and tissue and the selective pressure upon cancer cells by antitumor mechanisms, cancer transcriptional programs exists in a discrete set of possibilities, rather than a "continuum" of tumor transcriptome. More specifically, in the context of cancer acquisition, there is a natural homeostatic robustness in the underlying regulatory network between the elements of the TME that arise from the presence of redundancies in cell signaling mechanisms, such as regulatory feedback and feedforward loops. This homeostatic robustness was initially intended, in the healthy tissue, to implement some functionalities, such as the capability to buffering small interruptions in cell signaling processes, cell signal memory and the integration of continuous input signals into a "all-or-none" response by using a hysteresis mechanism [23]. As a side effect, it prevents the TME to exist in some transient and non-functional erratic states and favors others more robust against small spurious changes. Among the latters, there are some immunocompetent states that get rid of the cancer cells (healthy attractors), but, unfortunately, there are others that are immunotolerant and allow the tumor growth (cancer attractors).

In other words, the very same network backbone that keep a tissue in a healthy or physiological state carrying out normal functions may maintain the system locked-in cancer states, which behave robustly against perturbations, including therapeutic intervention [24]. Consequently, identification and monitoring the constituent elements of network stability motifs may have an interest, and it has been proposed as strategy to find both biomarkers and therapeutic targets [25].

In this context, cancer acquisition can be visualized as a critical state transition in the cancer stability landscape (from now on, cancer landscape) from healthy to disease (cancer) attractors, so is the cure or the effective response to therapeutic checkpoint blockades in the opposite direction [7]. In this cancer landscape one may focus on the characterization and mechanistic elucidation of the unperturbed cancer attractors, or on the transitions and trajectories along this landscape in response to perturbations (see figure 1). The former refers to more description oriented modeling approaches and cancer-driving mechanism discovery, whereas the latter is typically associated to the discovery of novel targets for therapeutic intervention and the corresponding response mechanisms.

Figure 1: Toward integrative models of solid tumors: perturbed and unperturbed tumor microenvironment (TME.) Experimental information from unperturbed (untreated) and perturbed (treated) TME can be used to assemble models that describe cancer-driving and treatment response mechanisms. Such integrative models, would allow not only characterizing different types of healthy and cancer attractors, but also predicting how to transit from undesired to desired states in the cancer stability landscape.

Current limitations and future directions of experimental and computational models of the TME

In order to be able to navigate the cancer landscape and predict response to cytotoxic or targeted therapies in individual patients, we need models that capture the TME complexity, deal with both intra- and inter-tumoral heterogeneity, and preserve the spatiotemporal architecture of the TME [26]. That starts, first of all, with the biological model and experimental assays, and secondly, by the adopted modeling formalism according to the intended purpose of the model. In other words, it is unlikely that a given process that relies on the interplay between different cell types is properly described by a model constructed using data from an experimental platform that does not include all relevant players or using a mathematical representation that neglects such interplay or the spatiotemporal distribution of the participants.

Unfortunately, current standard in vitro and ex vivo experimental platforms based on cell lines and spheroids or organoids are limited in their ability to mimic the native tumor, which yields a poor mapping to clinical outcomes [7]. Efforts have to be done in the direction of preserving cellular and microenvironmental complexity and heterogeneity, as well as the spatiotemporal architecture, as they have been pointed out as contributing factors in the variability of response to therapy [26].

Computational models of the TME can be constructed with different levels of mechanistic detail and compartmentalization, and the fidelity of the resulting cancer landscape will follow accordingly. Bulk tumor-tissue models can be useful to describe or to get insights into global TME behavior, but they may fail to describe crosstalk between specific cellular components of the TME. To this end, it may be reasonable to construct multicellular models to deal with tumor cellular heterogeneity, where the model explicitly considers different cell types, such as in agent-based models (see table 1).

Nowadays, there are two general approaches to achieve such a multicellular model: 1) Mathematical/computational deconvolution from bulk-tumor experimental information; and, 2) Model construction based on experimental information from single-cell technology. Putting together experimental data from single-cell technology in a multicellular model can be described as a horizontal integration, in contrast with a vertical integration, which is the integration of different types of-omics, phenotypical and clinical data in a so-called multi-scale model. Different biological scales relevant for cancer modeling operate at different spatial and temporal ranges; multi-scale modeling requires establishing a linkage between these scales [27].

Model deconvolution in different cell types and the assembly of multi-scale models by data integration, as well as the spatiotemporal compartmentalization, seem promising strategies to capture the complexity and partially address the heterogeneity of the TME, specially under the promises of single cell technology, However, modeling based on this sensitive technology faces new challenges; single cell technologies such us single cell RNA-seq open the possibility of detection of new subpopulations of cells but also open the gates to confounding factors such as the cell cycle and other oscillatory processes, which constitute a source of heterogeneity [28].

Teasing apart these sources of heterogeneity is needed in order to robustly identify functionally distinct subpopulations of cells and to construct suitable multicellular models.

Apart from the horizontal and vertical integration of data, there is yet a third type: the integration of cancer-driving and response mechanisms of unperturbed (untreated) and perturbed (treated) TME respectively. Traditionally, these are two different aspects of the TME that have been studied separately. However, it seems reasonable to assume that models able to predict response to specific treatments in specific patients would require the integration of a comprehensive list of both cancer-driving and response mechanisms and an individual patient profile on the status of such mechanisms. Both the elucidation of mechanisms and the identification of biomarkers reporting their status in individual patients are challenging, and they require either a significant amount of perturbation experiments to construct the models or prior knowledge on the underlying mechanisms or both, as well as massive patient population bioinformatics analysis to characterize individual or groups of patients [29]. Thus, the construction of predictive models able to identify responders and non-responder to specific treatments is an ongoing task.

In this article, we review what has been achieved in modeling and simulation of the TME so far and comment on current and future challenges.

Modeling the Unperturbed TME: Discovery and Description of Cancer-Driving Mechanisms

Modeling the unperturbed TME refers here to the description of the tumor behavior in the absence of therapeutic intervention. These models attempt to elucidate and simulate cancer-driving mechanisms as they normally perform in order to facilitate tumor growth.

Studying dysregulated pathways with and without oncogenic mutations in cancer cells

Traditionally, the identification of dysregulated pathways in cancers has been bound to oncogenic mutation previously known. Oncogenic mutations in some genes can induce neoplastic transformation of cells by changes in specific pathways of the underlying regulatory network that eventually determine the cellular program [30]. Some of these changes are easy to anticipate, such as those in proteins directly regulated by a mutated gene, whereas others can affect proteins far away downstream in the pathway and can only be pointed out under the scrutiny of systems modeling [31]. There exist examples of this kind of model-based studies in some of the most commonly mutated pathways in cancer, such as p53 [8], RAS [7], GCSFR [32], and the ErbB family of receptors [7]. The experimental part of these works was based on different cancer cell lines, and the adopted modeling formalism include both deterministic and probabilistic approaches, such as mass action ODE models [33] and weighted linear combinations [34] in the former, and partial least square regression [35], stochastic simulations based on Gillespie algorithm [36,37] and Galton- Watson branching processes [32], in the latter.

Under the paradigm of systems biology, it is also conceivable that intact cellular networks exhibit dysregulation for specific pathways, for which no constituent element is affected by oncogenic mutations. In other words, under this systems perspective, most dysregulated pathways of a mainly intact cellular machinery are just operating differently because the system is trapped in a cancer attractor [22] or a self-maintained state that differs from a normal state, and which has been reached by the action of a reduced number of triggering factors or mutations. That was something observed by Mani et al. [37], when investigating dysregulated pathways in human tumor related versus unrelated B cells for three kinds of non- Hodgkin's lymphomas by using a network-based model inferred from transcriptional data.

Similar works are the one proposed by Chang et al. [38] on effector pathways downstream of RAS by combining a protein-protein interaction network with transcriptomics data by linear regression of gene expression data with respect to the signature defined by specific network modules, and the one by Heiser et al. [39] on the activation of the ERK pathway by ErbB family receptors in breast cancer using a logic-based model constructed from literature and trained using transcriptomic and proteomic data.

There also exist models to describe the impact of mutations on the intra-tumor heterogeneity, such as the model proposed by Howk et al. [40] to explore the role of the accumulation of a large number of genetic alterations as main driving force in oncogenesis, rather than the traditional biological perspective of the driving role of a small set of genetic mutations. In this case, the model exhibits certain vertical integration resulting in a multiscale model where different scales were described using different modeling formalisms; the time required for a cell to divide or die is governed by a set of ODE, and the fate of each individual cells is subject to stochastic variation and calculated through Monte Carlo simulation.

Altogether, these works on the impact of oncogenic mutations have contributed to understand the existence of heterogeneity at cancer cell levels and to enumerate a variety of possibilities to affect the same and different cancer associated pathways. Moreover, some of them were even intended to explicitly describe the intratumor heterogeneity in cancer cells [40].

The description of these mechanisms is of course only part of the puzzle. The link between them and a phenotypic outcome, such as cell death or survival, is strongly intertwined with the other elements of the TME, such as infiltrating immune cells, which are not explicitly considered in these cancer-cell-centric models.

Models of tumor growth and angiogenesis in the unperturbed TME

Tumor growth is a classical cancer related event described with the assistance of mathematical models, and, especially ODEbased models. In general, these models describe the tumor volume in time as a function of some variables and parameters. Depending on the type of equations there are different categories of ODE-based models that have been used to describe tumor growth, which may differ in predicted outcome and be more suitable for specific tumor types. Among the most frequently used we find exponential [41], Mendelsohn [42], logistic [43], linear [44], surface [45], Bertalanffy [46] and Gompertz [47], which have been recently reviewed and compared [48].

In general, exponential models are suitable to describe early stages of tumor growth, when the population of cells divides regularly producing two daughter cells for each parental cell and there is homogeneous availability of oxygen and nutrients. However, exponential models fail when the tumor reaches a critical mass and angiogenesis and nutrient depletion play a role [47,48]. The other categories of ODE-based models for tumor growth try to overcome the tumor size scalability problem including parameters to correct the overestimation of the exponential model or assuming an initial exponential growth that becomes linear over time.

Apart from these ODE-based models of tumor growth, there are other more modern models, which rely on the description of the underlying mechanisms. A remarkable example of a multiscale model of avascular tumor growth is the work of Jiang et al. [49,50], where processes, such as cell proliferation, transit and consumption/production of nutrients/wastes, adhesion and cell-environmental interactions are integrated using different probabilistic and deterministic modeling formalisms: lattice Monte Carlo model for cellular dynamics, Boolean networks for the subcellular level, and a system of ODE for the chemical dynamics.

At some stages of tumor growth, the center of the tumor becomes hypoxic and necrotic and the tumor needs its own vasculature to keep growing. Consequently, angiogenesis has attracted attention as a cancer driving mechanism to be described and as potential point for therapeutic intervention. As illustrative example of works on angiogenesis, Finley et al. [51] proposed a VEGF centered angiogenesis model trained against in vivo experimental data for the levels of free and bound VEGF Trap in mice bearing human tumor xenografts in order to predict the endogenous rate of VEGF secretion by myocytes and endothelial cells, which can only be measured in in vitro experiments. The model includes a set of ODEs to describe how the species' concentrations vary in time in three compartments (normal tissue, blood and tumor) and an equation for the tumor volume. Focused on other aspects of angiogenesis, Su et al. created a multicellular ABM model of cell growth in myeloma, where they simulate the effect of SDF1 induced chemophysical communications among different types of cells [52]. With the idea of a global multicellular-multiscale-integrative model in mind, modeling tumor growth/size and angiogenesis is arguably important, as they may influence the intratumor heterogeneity overtime. Hypoxia gradients and its evolution are relevant for predicting the global and local TME behavior, as they influence the neovascularization and immune cells attraction, extravasation, migration and activity, which are ultimately related with the patient response to therapy and tumor dissemination.

Models of tumor invasion

Modeling mechanisms of tumor invasion has attracted attention, as they are related with both tumor progression in the native location and metastasis. Due to that, biomarkers reporting the activity of these mechanisms in the unperturbed TME have prognostic value in terms of overall or relapse free survival and can be potentially used for patient stratification.

Tumor invasion is influenced by chemical factors and physical forces needed for the degradation of the host tissue. Concerning the former, there are some attempts to model these events, mainly centered on the tissue degradation by metalloproteinases (MMP). Deakin and Chaplain [53] proposed an ODE-based model focused on both soluble and membrane-anchored MMP and their role in degrading collagen structures and cross-linked fibers. Mumenthaler et al. [54] proposed an ODE-based model (reaction-difussion equations) to describe the tissue degradation process centered on the description of the MMP concentration and the density of the extracellular matrix.

Concerning methods modeling physical forces, Mitchell and King [55] recently reviewed computational and experimental models of the cancer cell response to fluid shear stress, including cell exposure to interstitial flows [56] and mechanotransduction phenomena [57] and cell behavior in the circulation [58].

Katire et al. [59] discussed computational modeling describing the effect of changes in both cellular [60,61] and extracellular [62,63] mechanical properties, such as stiffness and adhesivity, and identified mechanistic pathways for cancer progression.

In general, tumor aggressiveness is very much determined by its capacity to disseminate, which can be partially reported by monitoring the activity of mechanisms of tumor invasion. Consequently, predictive models of the TME would very much benefit from considering these mechanisms and characterizing them across patients.

Identification of biomarkers in the unperturbed TME

Biomarkers can be defined as measurable indicators of biological processes, which can be either normal or pathogenic. In oncology, they may also report the biological response to a therapeutic intervention in the perturbed TME and be used as predictors of clinical outcome and to classify patients in responders and not responders to specific treatments. However, the complexity of the immune response in the TME hinders the identification of reliable biomarkers across different datasets of patients. Network-based modeling constitutes an approach to deal with this complexity and ease the identification of indicators of good or bad prognosis.

Network analysis of high-dimensional molecular data allows the identification of highly connected nodes (hubs) [64] and central nodes (bottlenecks) [65], as well as sets of highly interconnected nodes (modules) [66,67]. Hubs are arguably good potential biomarkers, as they may report the activity of many other interacting nodes, whereas the identification of modules is more related to the discovery of cancer-driving mechanisms or pathways. The validity of these biomarkers is commonly supported by their statistical association to clinical traits, such as patient survival. Examples of this approach are the identification of driving genes in brain cancer invasion [68] and breast cancer oncogenesis [69].

Rather than trying to construct and analyze a global network, one may focus on the identification of small network motifs of few genes with specific properties in order to find relevant biomarkers. More specifically, network motifs conferring bi-or multi-stability are particularly interesting, as they shape the cancer landscape; both healthy and cancer attractors requires their existence. These motifs constitute biological switches involved in a number of biological processes such as cell differentiation [70], the mitogen-activated protein kinase (MAPK) cascade [71,72], receptor tyrosine kinase activation [73], and cell cycle regulation [74]. Consequently, the constitutive elements of such motifs are potentially interesting biomarkers and drug therapeutic targets. Large scale search of bi-stable motifs in a prior knowledge network derived from literature allowed the identification of switches including interesting biomarkers in lung cancer and hepatocellular carcinoma [25], such as, the bi-stable toggle switches between FN1 and SPP1 and between EDN1 and; SPP1 is a negative survival factor in patients with non-small cell lung carcinoma (NSCLC) [75], whereas the expression of the hypoxiainducible angiogenic growth factor EDN1 is associated to poor prognosis in NSCLC [76].

Integrative models of the TME should definitely consider biomarkers of the unperturbed TME, as they may report the status of a variety of cancer driving mechanisms and can be characterized across patients. However, the tumor architecture has to be taken into account, as different regions of the tumor may operate through different cancer-driving mechanisms, which may imply differences in drug sensitivity and prognosis. That lead us to the idea of monitoring different regions of the tumor, rather than a bulk-tumor biomarker assessment. Of course, this is something not feasible in most of current standard experimental platforms.

Modelling Perturbations of the TME: Describing Response to Therapy and Identification of Therapeutic Targets and Biomarkers

Perturbation of the TME refers in this context to therapeutic interventions. Modelling the perturbed TME attempts to describe and predict the tumor response to specific therapies and to find novel therapeutic targets and biomarkers of the adequacy of a given treatment for a given patient. In the attempt to improve the response to cancer treatment, different constituent elements of the TME have been explored as potential therapeutic targets during the last decades of cancer research [77], such as tumor cells, different elements of the immune system, and events related to tumor growth and accessibility, like angiogenesis or the composition of the extracellular matrix. In general, combined therapies that allow simultaneously targeting multiple robustness features or weaknesses of a specific tumor, has been envisioned as a promising strategy to increase response rates, decrease tumor recurrence and minimize adverse reactions [78].

Combined therapy targeting multiple subpopulations of tumor cells

Deep sequencing has revealed a vast genetic heterogeneity that exists in individual tumors. This intratumor genetic heterogeneity explains why both de novo and acquired resistance arise with both molecularly targeted drugs and cytotoxic chemotherapy, which limits the effectiveness of conventional single treatment approach by both decreasing response rates and increasing tumor recurrence.

One solution for the problem of cancer drug resistance is a well-designed combinatorial therapy. Examples of current effective combinations are trastazumab in combination with paclitaxel in breast cancer [79] and cetuximab in combination with irinotecan in colon cancer [80].

However, the scale of the combinatorial problem of finding effective combinations is challenging. There is need for methods to evaluate and prioritize the best candidates for further experimental evaluation, and computational approaches are being applied for this purpose. Currently, there exist a variety of different modeling approaches, but they all have in common the construction of an initial model based on prior knowledge or inferred from data by data-driven approaches, which is subsequently enriched by model training or internal validation based on known test data. Experimental validation or invalidation of predictions can be iteratively used to improve the model. For example, Darwinian models have been applied in NSCLC to identify optimal combinations and posology for EGFR inhibitors gefitinib and erlotinib for delaying the evolution of resistant mutants [81], and to identify that sequential treatments using cytotoxic agents in combination with erlotinib or gefitinib are more effective than single treatment or concurrent combination dosing [82].

Alternatively, to the static view of the evolutionary tree constructed based on genomic data of Darwinian models, one may consider to monitor a tumor in time and predict dynamic vulnerabilities. The so-called "temporal collateral sensitivity" refers to the phenomenon induced by a drug of transient tumor sensitization to other drugs. Genotypic, phenotypic, signaling and binding measurements can be combined in stochastic (probabilistic) computational models to adapt the therapy in time in order to exploit these vulnerabilities [83].

More focused on the description of the underlying mechanisms there exist a variety of network-based models to find drug combinations or synergy. For example, a model of the ErbB pathway was proposed to explain the limited benefits of gefitinib treatment in lung cancer for tumors with wild-type EGFR with respect to those with a deletion of exon 19 and a point mutation L858R, which are associated with elevated phosphorylated AKT and sensitivity to tyrosine kinase inhibitor gefitinib [84]. This model is a deterministic massaction ODE based and includes the receptor internalization mechanism and activation of ERK and AKT. Simulation of this model indicated that differences in signaling observed between wild-type and mutants rely on a slower EGFR internalization. In another example, phosphoproteomic data before and after IGF-1 stimulation in MDA-MB231 human triple-negative breast cancer cells was used to construct a mass action model of the IGF-1 signaling network [85]. This model was used to verify that the combination of MAP4K and PI3K/AKT pathway inhibitors provides synergistic effect in reducing cell viability, whereas the combined inhibition of MAPK and mTOR pathways activates AKT and increase cell viability.

Computationally predicting drug combination response typically relies on extensive perturbation data. Alternatively, one may consider constructing models based on data from the unperturbed TME and prior knowledge about regulatory interactions to predict the response to single or combined treatments. Flobak et al. [86] reported a computational approach to discover drug synergies in gastric cancer by logical modeling based on baseline (unperturbed) proliferative state of tumor cells derived from literature and databases, which integrates information about MAPK pathways (JNK, p38 MAPK and ERK), the PI3K/AKT/mTOR pathways, the Wnt/β-catenin pathway, and the NF-κB path-way, as well as crosstalk between these pathways. The model is focused on specific cancer cell biomarkers obtained from unperturbed tumor cells and allowed the authors to identify by automated logical reasoning synergistic drug combinations to inhibit tumor growth. Four out of five of these predicted combinations were experimentally validated afterwards, which confirmed the utility of the method to contribute to preclinical discovery or effective anticancer drug combinations.

Rather than trying to elucidate and integrate a detailed mechanistic description, including all the constituent elements of relevant cancer-related pathways, one may consider a pair-wise approach to identify single and combined cancer treatments. More specifically, cancer vulnerabilities can be identified by detection of the so-called "synthetic lethality", which refers to the situation when the inhibition of two genes is lethal for cancer cells, whereas the inhibition of each single gene is not. Knowledge about these synthetic lethality events opens opportunities to selectively attack cancer cells with drugs that target the pair of a gene who is inactive only in these cancer cells [87,88]. A closely related concept is the so-called "synthetic dosage lethality", which refers to the phenomenon when the overactivity of one gene renders other gene essential for cell survival. This type of events is particularly interesting to selectively attack cancer cells with overactive oncogenes that are difficult to target directly by targeting the synthetic dosage lethality partners.

A number of screening technologies have been developed to detect synthetic lethality and synthetic dosage lethality in model organisms [89,90], human cell lines [7] and based on human cancer genomic data. In the latter case, the increasingly accumulated cancer genomic data has allowed the data-driven construction of synthetic lethality and synthetic dosage lethality probabilistic networks, and correctly identify these events for the tumor suppressor VHL and predict gene essentiality and clinical prognosis [91]. Synthetic dosage lethality has also been investigated in the human metabolic network, and it has been shown that it is highly predictive of tumor growth and clinical outcome [92].

In general, modeling efforts to target multiple subpopulations of tumor cells reflects the need to deal with intratumor heterogeneity, but it only refers to the variability in the cytotoxic effect on cancer cells of a given treatment. Other aspects of this intratumor heterogeneity, such as the heterogeneity of TIL, is not considered at all by these models and it has to be addressed in integrative models intended to predict the global clinical outcome of specific patients.

Enhancing the antitumor immune response in the TME

Activating the immune system for therapeutic benefit in cancer has been a goal in cancer research for years, but only recently cancer immunotherapy has become a reality [93].

Different immune cells can have both antitumor and pro-tumor effect, and they interact with each other and with other components of the TME in a very convoluted regulatory network; predicting the overall effect on the immune activity of targeted therapies interfering this network is difficult. Models can assist to better understand this complex biology and predict effective and combined ways to influence the system toward a competent immune response by directly targeting immune cells activity or by enhancing the immunogenicity of tumor cells. There are several examples of the latter case, such as increasing cancer cells antigenic burden by selectively introduce DNA damage, arresting tumor growth by MEK1 inhibition, inducing apoptosis by mTOR inhibition, etc [93]. In another example, a deterministic logic-based model of RAW 264.7 mouse leukemic macrophages showed that, despite a model simplification to reduce the complexity of the drug combination design problem, relevant cross-talking between signaling pathways was preserved, providing a sufficient condition under which the drug combination effect could be maintained. Subsequently, the model was used to identify three synergistic drug combinations on nuclear factor Kappa B (NF-κB) pathway, which were experimentally verified [94].

These works based on the perturbation of individual or multiple mechanisms or pathways constitute the foundation of the antitumor immune response in future integrative models. However, despite these works have shown their utility to identify suitable targets to boost the antitumor immune response, the resulting predictions and validations referred to the average behavior in the biological model and experimental platform used to construct and train these models, for which the TME may differ dramatically with respect to patient’s reality and diversity.

Once more, there is need for experimental platforms that preserve the global tumor architecture and spatiotemporal characteristics in order to capture the complexity and heterogeneity of the TME, and for computational models based on these experimental platforms that explicitly consider all the elements of this complex system and their intra- and intertumor variability. Otherwise, model prediction may be correct but refer solely to experimental conditions far away from the patients TME.

Models of tumor growth and angiogenesis in the perturbed TME

There are several elements of the stroma of solid tumor that promotes tumor growth and may confer protection against the antitumor immune response, such as endothelial cells, cancer-associated fibroblasts, mesenchymal stromal cells, the extracellular matrix and tumor vasculature. However, there is an intrinsic difficulty in targeting these components, as they usually play a role in normal tissues and processes. It has been suggested that some of these processes, such as the regulation of the composition of the extracellular matrix, rely on 'protease web' or a set of interconnected pathways that should be studied with a systems approach using network-based models [95], and there exist some attempts to do that [7]. However, only some of these processes, such as angiogenesis, have been investigated with the assistance of computational modelling to find therapeutic targets. It is commonly accepted that neovascularization is essential for tumor growth and cancer progression in solid tumors. Despite the multifactorial and multicellular nature of angiogenesis, TIE-2 expressing monocytes (TEM) have been distinguished for being critically involved in this process. Therefore, there is a keen interest on dampening the angiogenic activity of TEM as therapeutic strategy. However, the angiogenic activity of TEM is adopted after the tumor infiltration and shaped by the complexity of the tumor microenvironment, which hinders the elucidation of the molecular basis of such activity. Using a deterministic logic-based model of monocyte behavior inferred from single and double perturbation experiments, Guex et al. identified several minimal combined treatments capable to reverse high-angiogenic TEM to a low-angiogenic phenotype more similar to circulating monocytes, which were experimentally verified using TEM derived from breast cancer patients [96]. Examples of these minimal treatments are the inhibition of TIE-2 kinase combined with TGF-β, and simultaneously engaging VEGFR-1 using either VEGF or PIGF. Treated patient derived TEM exhibited less angiogenic activity in a mouse cornea vascularization assay than non-treated.

Another logic-based model of the inflammatory angiogenesis-related NF-κB pathway in endothelial cells using dose-response data for drugs targeting pathway elements was used to identify drug synergies, such as the combination of geldanamycin, a HSP90 inhibitor, and PS-1145, a IκB kinase (IKK-β) inhibitor [97].

There are several works using ABM models in the direction of mimicking the dynamic tissue changes in solid tumors. Wang et al. constructed an ABM-based model of melanoma cancer that integrates angiogenesis and tumor growth under combined therapy [98]. Similarly, using a hybrid multi-scale ABM, Ji et al. predicted the impact of combined therapies on myeloma cell growth [99]. Within this model, intracellular signal transduction events were described using ODE, whereas cellcell communication between cancer cells, stroma cells and immune system were described using ABM formalism.

In general, most of current modeling efforts of tumor growth and angiogenesis in the perturbed TME describe the effect of specific treatments on these processes without considering other processes of the TME, such as the antitumor immune response, nor the heterogeneity of the response within and across tumors. Concerning the latter, most of these models are oversimplifications from the mechanistic point of view, as they are constructed as a cause-effect relationships network from the experimental data. This lack of mechanistic detail and the corresponding biomarkers reporting the activity of different parts of these mechanisms prevent the proper characterization of the response across different tumor regions and patients. Catalogues of response variants together with the associated individual patient profiling would overcome tumor heterogeneity issues, but only the integration of these mechanisms with other relevant processes taking place in the TME would consider all the components involved in the clinical outcome.

Identification of biomarkers in the perturbed TME

Biomarkers of an antitumor response evaluated on baseline (unperturbed) tumor samples may have a limited predicting value due to stochastic events. Alternatively, in order to anticipate whether a patient will be benefited from a specific treatment, it has been proposed the identification of the so-called dynamic biomarkers [100]. The basic idea is that the evaluation or identification of these dynamic biomarkers is carried out early during treatment, which enables the detection of patients who may benefit from continuing or not. This strategy is arguably more robust to predict the patient response and despite it is suboptimal (pre-treatment detection of biomarkers would be better if accurate), it could be of great value. Moreover, these dynamic markers may be better indicators of the underlying mechanism of action of the treatment or even being actionable biomarkers; they conform the dynamic network biomarkers or leading subnetworks that move first after treatment toward the final state, hopefully, an immunocompetent attractor. In the context of immune checkpoint blockade with CTLA4-specific antibody, this strategy allowed to identify two response-associated modules and NOS2 as hub in mice [101]. The relevance of this finding was validated by pharmacologically inhibiting or enhancing the biological activity of NOS2 and observing the corresponding changes in responses rates to CTLA4 blockade.

Identification of biomarkers reporting the activity of response mechanisms is essential to deal with both intra- and inter-tumor heterogeneity, but the tumor architecture has to be taken into account, as different tumor regions may have different response. Unexpected drug resistances may appear if some parts of the tumor that are not sensitive to the treatment take over tumor growth, as they are favored by the drug selective pressure, and dramatically change the clinical outcome. This issue would suggest that, similarly to the unperturbed TME case, the biomarker evaluation should be carried out in different regions of the TME, which demands an experimental platform where such a thing is possible.

Using computational modelling to assist on the drug design

Computer-aided drug design (CADD) methods, including modeling techniques, have been used for decades and extensively reviewed recently [102]. Some of these methods neglect the underlying action mechanism or even the molecular target, such as those focused on detecting similarities to previously known active ligands. However, nowadays, modern targeted cancer therapy development has two components: figuring out what mechanism or combination of mechanisms we want to target and the design of the appropriate molecules for this purpose. In this review we focus on this more mechanistic and systems-oriented approach, and, in particular, on single and combined target discovery; we just briefly mention the main drug design methods for completeness, as the molecular docking of ligand and targets is also a modeling technique used in cancer research.

Drug design

CADD methods has played a relevant role for decades [102]. These methods can be classified in structure-based and ligand-based approaches. In structure-based approaches, the information about the structure of both ligands and targets is relevant, and they rely on 2D or 3D molecular modelling. Structure-based approaches include protein-ligand docking [103,104], pharmacophore [105], and de novo ligand design methods [106,107]. Ligand-based methods only use ligand information, and the activity of new molecules is predicted based on the similarity to previously known active ligands [108,109]. It is worth mentioning that the same methods used to predict activity could be used to predict toxicity, drug metabolism and pharmacokinetics [110,111].

Cancer Vaccination and Neoantigen Prediction with the Assistance of Computational Modelling Approaches

Cancer vaccination has recently migrated from targeting tumor-associated self-antigens, i. e., proteins that may be aberrantly expressed and presented in cancer cells, to targeting neoantigens result of tumor specific somatic mutations.

The process of selecting immunogenic peptides starts with the identification of somatic mutations by exon sequencing of a cancer biopsy and normal tissue, and transcriptome data is also frequently used to estimate and select the most abundant antigens, assuming antigen abundance as necessary condition to induce an effective immune response. By doing so, some suitable neoantigen candidates can be identified, but still the key question is whether or not these mutated proteins will be processed into 8- to 11-residue peptides by the proteosome, transported into the endoplasmic reticulum and loaded into the major histocompatibility complex class I (MHC-I) for recognition by CD8+ T cells.

There exist computational methods based on artificial neural networks focused on modeling antigen processing (NetChop[112]) and peptide transport (NetCTL [113]), but most efforts are directed to model and predict which peptides will bind the MHC-I (NetMHC [114,115]). It is worth noting here that future directions should arguably include predicting MHC-II binders, which is essential for CD4+ T cells antitumor response.

It is worth mentioning here the Tumor Neoantigen Selection Alliance, an international initiative involving researchers from 30 universities, non-profit institutions and companies, which attempt to address the challenges of developing and benchmarking software tools for predicting MHC binders.

Models of adoptive cell transfer immunotherapy

In the realm of adoptive cell transfer, dendritic cells are a promising immunotherapy tool for boosting the adaptive immune system. DePillis et al. [116] developed a mathematical model based on differential and delay-differential equations to describe the interactions between dendritic cells, T effector cells, and tumor cells in melanoma. This model considers immune cells trafficking between lymph, blood and tumor compartments, and it was used to suggest dose, location and schedule modifications to enhance immunotherapy efficacy.

Models to Improve Treatment Modalities

Treatment efficacy, including surgery, radio- and chemotherapy may benefit from complementary treatments. There exist computational modeling approaches to study treatment related events in the attempt to maximize treatment efficacy

For example, Kim et al. [117] proposed a multi-scale hybrid model centered on microRNAs that balance cell proliferation and migration under different microenvironmental conditions in glioblastoma. This model suggested that post-surgery injection of combinations of chemoattractants and glucose reduces the diffusive spread of residual cells after tumor removal, leading to a more effective therapeutic strategy to eradicate tumor cells.

Hawkins-Daarud et al. [118] proposed an ODE-based model to describe the intratumor edema under anti-angiogenic treatments in glioma. This model integrates different cell populations, (normoxic, hypoxic and necrotic cells) competing for space. Simulated glioma growth suggested that antiangiogenic treatment could serve as a surrogate for steroids, which was supported by comparison with real magnetic resonance images

Rejniak et al. [119] developed a computational model of interstitial transport that integrate the biophysical properties of the tumor tissue in order to describe penetration and efficacy of therapeutic agents.

Roadmap for the Future

The new era of personalized oncology demands an experimental platform closer to the actual TME of individual patients, and the assistance of computational models in the experimental design in order to make the development of novel and personalized therapies cost-effective.

To this end, both the experimental platform and the computational models have to capture the complexity and heterogeneity of the TME, which requires the preservation of TME architecture and the consideration of the spatiotemporal distribution of its constituent elements. For this purpose, we highlight here four main features that models of the TME should ideally exhibit: multicellular deconvolution, spatiotemporal compartmentalization, multiscale, and, the integration of both cancer-driving and response mechanisms.

Concerning the model deconvolution; one of the pitfalls when modeling the TME from bulk-tumor experimental data is that the information from different cell types, including different subpopulations of cancer and stromal cells and phenotypic variants, is merged in an average signal, which hinders the identification mechanisms and biomarkers. The analysis of great number patients by integration of multiple data sets from bulk-tumor experiments and the computational deconvolution [120] of the constituent cells of the TME can overcome this problem and help on the stratification of the population of patients and characterization of the different modes of antitumor immune response [29]. However, this computational deconvolution requires profiling the constituent cells of the TME, which is usually done by using purified cell types. A better profiling of individual cells obtained from experimental systems closer to the in vivo reality and that captures cell type heterogeneity is required for a proper model deconvolution.

Alternatively, single cell technologies, such as single cell RNA-seq, can be used for model deconvolution. However, these technologies face a new generation of problems. In particular, this technology allows the identification of a myriad of subpopulation of cells, some of them resulting from potential confounding factors, such as the cell cycle and other oscillatory cellular processes [28]. Clustering groups of cells functionally similar based on a heterogeneous transcriptional profile refers to the problem of connecting transcriptome and phenotype, and despite it is not clear in what extent this problem has to be addressed in order to assemble reliable multicellular models from single cell technology by "reconvolution" or horizontal integration, arguably, techniques to filter out major confounding factors have to be developed [28].

Concerning the spatiotemporal compartmentalization; depending on the intended purpose of the model, the deconvolution or horizontal integration can be done at different degree of granularity, such as cell subtypes, types, lineages or any sort of clusters according to the scientific question. Some modeling formalisms, such as ABMs (see Table 1), are remarkably flexible for that purpose. However, the spatiotemporal distribution of the elements of the TME has to be taken into account, as the total or relative composition of TME cell populations may change overtime and differ in different regions of the tumor. For example, the total count of TIL may be very different before and after treatment, and peripheral TIL (excluded infiltrate) have to be explicitly distinguished by the model from internal TIL, or the response to immunotherapy could be wrongly predicted.

Apart from this multicellularity and spatiotemporal compartmentalization, which refer to horizontal data integration, there is another type of integration that is required. In both the unperturbed and the perturbed TME, only certain level of mechanistic description would allow making predictions robust across different patient datasets, as differences in these underlying mechanisms can be characterized, monitored and explicitly considered by the model. That implies a vertical integration of different levels of complexity to result in the so-called multiscale models, being the main difficulty in this integration for known mechanisms establishing a linkage between these levels or scales, which may operate, for example, at different orders of magnitude in time and space [27]. However, a great deal of these mechanisms is not known. A great effort has to be done in this direction and to identify suitable biomarkers that report the activity of relevant mechanisms, which may differ across patients or even tumor regions.

Despite traditionally, the unperturbed (untreated) and perturbed (treated) TME has been studied separately. Models of an unperturbed TME are usually constructed to describe cancer-driving mechanisms. On the other hand, models of a perturbed TME are usually applied to describe or simulate the mechanism of action of specific perturbations, such as treatments, and to identify novel potential therapeutic targets and biomarkers. However, from a translational point of view, it seems reasonable that integrative models including both cancer-driving and response mechanisms are required for practical clinical applications, as both types of mechanisms can be strongly intertwined, and the characterization of both in a given patient would be relevant to predict a clinical outcome.

Finally, a word of caution about modeling to assist on the experimental design. A major difficulty in the model construction using experimental data is that explaining a given output or set of experimental readouts as a function of a given initial conditions is often an underdetermined problem, implying that the model inference problem does not have a unique solution [121], which means that the model is not inferable from the data. However, models can also be interrogated to identify the minimal set of additional perturbation experiments required to render a non-inferable model into an inferable one in order to address specific questions or predictions [122]. Consequently, it is reasonable to envision future TME modeling efforts as an iterative and collaborative endeavor between experimentalist, clinicians and computational biologists, rather than a one-shot effort.

Conclusions

Modeling the TME has to deal with the intrinsic intra- and inter- tumor heterogeneity and complexity due to its multicellular nature, tissue architecture, and differences across patients. These heterogeneity and complexity have to be captured, first of all, by the biological model and experimental assays used to construct the mathematical/computational model, and secondly, by the adopted modeling formalism, which should consider the spatiotemporal distribution of the constituent elements of the TME. Modern ex vivo and organoid-based experimental platforms attempt to provide biological systems close to the actual TME of the patient, which arguably will result into more useful computational models from a translational perspective. In addition, single-cell high throughput technologies promise the deconvolution of the experimental information, which was previously derived computationally from bulk-tissue experiments.

However, the era of personalized medicine faces new challenges; modern TME computational models require a vertical integration of different sources of-omics, phenotypical and clinical data, which yields multiscale models, and a horizontal integration of deconvoluted information, which yields multicellular models.

Such multiscale and multicellular models capable to anticipate response to single and combined treatments in individual patients would require and integrative approach merging mechanistic description of both the unperturbed and perturbed TME, which refer to the characterization of the tumor in the absence and presence of treatments, respectively. The mechanistic description of such integrative model, together with patient profiling based on these mechanisms would allow customizing or fine-tuning a general model to specific patients or groups of patients, in order to design tailor-made therapies and successfully navigate the cancer landscape.

References

1. Holland JH. Studying complex adaptive systems. J systems science complexity. 2006;19:1-8.
2. Ladyman J, Lambert J, Wiesner K. What is a complex system? European J Philos Science. 2013;3:33-67.
3. Germain RN. The art of the probable: system control in the adaptive immune system. Science. 2001;293(5528):240-5.
4. Gajewski TF. The next hurdle in cancer immunotherapy: Overcoming the non–T-cell–inflamed tumor microenvironment. Semin Oncol. 2015;42(4):663-71.
5. Ji R-R, Chasalow SD, Wang L, et al. An immune-active tumor microenvironment favors clinical response to ipilimumab. Cancer Immunol Immunother. 2012;61(7):1019-31.
6. Tumeh PC, Harview CL, Yearley JH, et al. PD-1 blockade induces responses by inhibiting adaptive immune resistance. Nature. 2014;515(7528):568-71.
7. Majumder B, Baraneedharan U, Thiyagarajan S, et al. Predicting clinical response to anticancer drugs using an ex vivo platform that captures tumour heterogeneity. Nat Commun. 2015;6:6169.
8. Feinerman O, Veiga J, Dorfman JR, et al. Variability and robustness in T cell activation from regulated heterogeneity in protein levels. Science. 2008;321(5892):1081-4.
9. Subramanian VG, Duffy KR, Turner ML, et al. Determining the expected variability of immune responses using the cyton model. J Math Biol. 2008;56(6):861-92.
10. Buchholz VR, Schumacher TN, Busch DH. T cell fate at the single-cell level. Annu Rev Immunol. 2016;34:65-92.
11. Hodgkin PD. A probabilistic view of immunology: drawing parallels with physics. Immunol cell biol. 2007;85(4):295-9.
12. Murphy H, Jaafari H, Dobrovolny HM. Differences in predictions of ODE models of tumor growth: a cautionary example. BMC Cancer. 2016;16:163.
13. Jain RK, Martin JD, Stylianopoulos T. The role of mechanical forces in tumor growth and therapy. Annu Rev Biomed Eng. 2014;16:321-46.
14. Stylianopoulos T, Martin JD, Snuderl M, et al. Coevolution of solid stress and interstitial fluid pressure in tumors during progression: implications for vascular collapse. Cancer Res. 2013;73(13):3833-41.
15. Karlebach G, Shamir R. Minimally perturbing a gene regulatory network to avoid a disease phenotype: the glioma network as a test case. BMC Syst Biol. 2010;4:15.
16. Garg A, Di Cara A, Xenarios I, et al. Synchronous versus asynchronous modeling of gene regulatory networks. Bioinformatics. 2008;24(17):1917-25.
17. Ji Z, Su J, Liu C, et al. Integrating genomics and proteomics data to predict drug effects using binary linear programming. PloS one. 2014;9(7):e102798.
18. Ji Z, Wu D, Zhao W, et al. Systemic modeling myeloma-osteoclast interactions under normoxic/hypoxic condition using a novel computational approach. Sci Rep. 2015;5.
19. Stevenson C. Statistical models for cancer screening. Statistical methods in medical research. 1995;4:18-32.
20. Greaves M, Maley CC. Clonal evolution in cancer. Nature. 2012;481:306-13.
21. Little MP. Cancer models, genomic instability and somatic cellular Darwinian evolution. Biol direct. 2010;5:19.
22. Huang S, Ernberg I, Kauffman S. Cancer attractors: a systems view of tumors from a gene network dynamics and developmental perspective. Semin Cell Dev Biol. 2009;20(7):869-76.
23. Sabouri-Ghomi M, Ciliberto A, Kar S, et al. Antagonism and bistability in protein interaction networks. J Theor Biol. 2008;250(1):209-18.
24. Kitano H. Cancer robustness: tumour tactics. Nature. 2003;426(6963):125-5.
25. Shiraishi T, Matsuyama S, Kitano H. Large-scale analysis of network bistability for human cancers. PLoS comput Biol. 2010;6:e1000851.
26. Majumder B, Baraneedharan U, Thiyagarajan S, et al. Predicting clinical response to anticancer drugs using an ex vivo platform that captures tumour heterogeneity. Nat Commun. 2015;6.
27. Deisboeck TS, Wang Z, Macklin P, et al. Multiscale cancer modeling. Annu Rev biomed eng. 2011;13:127-55.
28. Buettner F, Natarajan KN, Casale FP, et al. Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nat Biotech. 2015;33(2):155-60.
29. Charoentong P, Finotello F, Angelova M, et al. Pan-cancer Immunogenomic Analyses Reveal Genotype-Immunophenotype Relationships and Predictors of Response to Checkpoint Blockade. Cell Rep. 2017;18(1):248-62.
30. Pawson T, Warner N. Oncogenic re-wiring of cellular signaling pathways. Oncogene. 2007;26(9):1268.
31. Bizzarri M, Cucina A, Conti F, et al. Beyond the oncogene paradigm: understanding complexity in cancerogenesis. Acta biotheoretica. 2008;56(3):173-96.
32. Kimmel M, Corey S. Stochastic hypothesis of transition from inborn neutropenia to AML: interactions of cell population dynamics and population genetics. Front oncol. 2013;3.
33. Birtwistle MR, Hatakeyama M, Yumoto N, et al. Ligand‐dependent responses of the ErbB signaling network: experimental and modeling analyses. Mol Syst Biol. 2007;3:144.
34. Kreeger PK, Mandhana R, Alford SK, et al. RAS Mutations Impact TNF-Induced Apoptosis in Colon Carcinoma Cells via ERK-Modulatory Negative and Positive Feedback Circuits along with non-ERK Pathway Effects. Cancer Res. 2009;69:8191-9.
35. Kumar N, Wolf-Yadlin A, White FM, et al. Modeling HER2 effects on cell behavior from mass spectrometry phosphotyrosine data. PLoS comput Biol. 2007;3(1):e4.
36. Leenders G, Tuszynski J. Stochastic and Deterministic Models of Cellular p53 Regulation. Front Oncol. 2013;3.
37. Mani KM, Lefebvre C, Wang K, et al. A systems biology approach to prediction of oncogenes and molecular perturbation targets in B‐cell lymphomas. Mol Syst Biol. 2008;4:169.
38. Chang JT, Carvalho C, Mori S, et al. A genomic strategy to elucidate modules of oncogenic pathway signaling networks. Mol Cell. 2009;34(1):104-14.
39. Heiser LM, Wang NJ, Talcott CL, et al. Integrated analysis of breast cancer cell lines reveals unique signaling pathways. Genome Biol. 2009;10(3):R31.
40. Howk CL, Voller Z, Beck BB, et al. Genetic Diversity in Normal Cell Populations is the Earliest Stage of Oncogenesis Leading to Intra-Tumor Heterogeneity. Front Oncol. 2013;3:61.
41. Collins VP. Observation on growth rates of human tumors. Am J Roentgenol. 1956;76:988-1000.
42. Mendelsohn ML. Cell proliferation and tumor growth. Cell proliferation. 1963:190-212.
43. Verhulst P-F. Notice sur la loi que la population suit dans son accroissement. correspondance mathématique et physique publiée par a. Quetelet. 1838;10:113-21.
44. Dethlefsen LA, Prewitt J, Mendelsohn M. Analysis of Tumor Growth Curves. J Natl Cancer Inst. 1968;40:389-405.
45. Patt HM, Blackford ME. Quantitative studies of the growth response of the Krebs ascites tumor. Cancer Res. 1954;14(5):391-6.
46. Vaidya VG, Alexandro FJ. Evaluation of some mathematical models for tumor growth. Int J Biomed comput. 1982;13(1):19-35.
47. Benzekry S, Lamont C, Beheshti A, et al. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput Biol. 2014;10(8):e1003800.
48. Murphy H, Jaafari H, Dobrovolny HM. Differences in predictions of ODE models of tumor growth: a cautionary example. BMC cancer. 2016;16:163.
49. Gerlee P. The model muddle: in search of tumor growth laws. Cancer Res. 2013;73(8):2407-11.
50. Jiang Y, Pjesivac-Grbovic J, Cantrell C, et al. A multiscale model for avascular tumor growth. Biophys J. 2005;89:3884-94.
51. Finley S, Dhar M, Popel A. Compartment Model Predicts VEGF Secretion and Investigates the Effects of VEGF Trap in Tumor-Bearing Mice. Front Oncol. 2013;3.
52. Su J, Zhang L, Zhang W, et al. Targeting the biophysical properties of the myeloma initiating cell niches: a pharmaceutical synergism analysis using multi-scale agent-based modeling. PloS one. 2014;9(1):e85059.
53. Chaplain M, Deakin N. Mathematical Modeling of Cancer Invasion: The Role of Membrane-Bound Matrix Metalloproteinases. Front Oncol. 2013;3.
54. Mumenthaler S, D'Antonio G, Preziosi L, et al. The Need for Integrative Computational Oncology: An Illustrated Example through MMP-Mediated Tissue Degradation. Front Oncol. 2013;3.
55. Mitchell M, King M. Computational and Experimental Models of Cancer Cell Response to Fluid Shear Stress. Front Oncol. 2013;3.
56. Swartz MA, Lund AW. Lymphatic and interstitial flow in the tumour microenvironment: linking mechanobiology with immunity. Nat Rev Cancer. 2012;12:210-9.
57. Tarbell JM, Shi Z-D. Effect of the glycocalyx layer on transmission of interstitial flow shear stress to embedded cells. Biomech Model Mechanobiol. 2013;12(1):111-21.
58. Paszek MJ, Boettiger D, Weaver VM, et al. Integrin clustering is driven by mechanical resistance from the glycocalyx and the substrate. PLoS comput biol. 2009;5(12):e1000604.
59. Katira P, Bonnecaze R, Zaman M. Modeling the Mechanics of Cancer: Effect of Changes in Cellular and Extra-Cellular Mechanical Properties. Front Oncol. 2013;3.
60. Katira P, Zaman MH, Bonnecaze RT. How Changes in Cell Mechanical Properties Induce Cancerous Behavior. Phys Rev Lett. 2012;108(2):028103.
61. Drasdo D, Höhme S. A single-cell-based model of tumor growth in vitro: monolayers and spheroids. Phys Biol. 2005;2(3):133-47.
62. Kim Y, Othmer HG. A Hybrid Model of Tumor–Stromal Interactions in Breast Cancer. Bull Math Biol. 2013;75:1304-50.
63. Montel F, Delarue M, Elgeti J, et al. Isotropic stress reduces cell proliferation in tumor spheroids. New J Physics. 2012;14:055008.
64. Barabasi A-L, Oltvai ZN. Network biology: understanding the cell's functional organization. Nat Rev Genet. 2004;5(2):101-13.
65. Yu H, Kim PM, Sprecher E, et al. The importance of bottlenecks in protein networks: correlation with gene essentiality and expression dynamics. PLoS Comput Biol. 2007;3(4):e59.
66. Hartwell LH, Hopfield JJ, Leibler S, et al. From molecular to modular cell biology. Nature. 1999;402:47-52.
67. Segal E, Friedman N, Koller D, et al. A module map showing conditional activity of expression modules in cancer. Nat Genet. 2004;36(10):1090-8.
68. Carro MS, Lim WK, Alvarez MJ, et al. The transcriptional network for mesenchymal transformation of brain tumours. Nature. 2010;463(7279):318-25.
69. Taylor IW, Linding R, Warde-Farley D, et al. Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat Biotechnol. 2009;27(2):199-204.
70. Crespo I, del Sol A. A General Strategy for Cellular Reprogramming: The Importance of Transcription Factor Cross‐Repression. Stem Cells. 2013;31(10):2127-35.
71. Markevich NI, Hoek JB, Kholodenko BN. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J Cell Biol. 2004;164(3):353-9.
72. Bagowski CP, Ferrell JE. Bistability in the JNK cascade. Current Biology. 2001;11:1176-82.
73. Reynolds AR, Tischer C, Verveer PJ, et al. EGFR activation coupled to inhibition of tyrosine phosphatases causes lateral signal propagation. Nat Cell Biol. 2003;5(5):447-53.
74. Pomerening JR, Sontag ED, Ferrell JE. Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat Cell Biol. 2003;5(4):346-51.
75. Boldrini L, Donati V, Dell'Omodarme M, et al. Prognostic significance of osteopontin expression in early-stage non-small-cell lung cancer. Brit J Cancer. 2005;93(4):453-7.
76. Boldrini L, Gisfredi S, Ursino S, et al. Expression of endothelin-1 is related to poor prognosis in non-small cell lung carcinoma. Eur J Cancer. 2005;41(18):2828-35.
77. Hanahan D, Weinberg Robert A. Hallmarks of Cancer: The Next Generation. Cell. 2011;144:646-74.
78. Al-Lazikani B, Banerji U, Workman P. Combinatorial drug therapy for cancer in the post-genomic era. Nat Biotechnol. 2012;30:679-92.
79. Slamon DJ, Leyland-Jones B, Shak S, et al. Use of chemotherapy plus a monoclonal antibody against HER2 for metastatic breast cancer that overexpresses HER2. N Engl J Med. 2001;344(11):783-92.
80. Sobrero AF, Maurel J, Fehrenbacher L, et al. EPIC: phase III trial of cetuximab plus irinotecan after fluoropyrimidine and oxaliplatin failure in patients with metastatic colorectal cancer. J Clin Oncol. 2008;26(14):2311-9.
81. Chmielecki J, Foo J, Oxnard GR, et al. Optimization of dosing for EGFR-mutant non–small cell lung cancer with evolutionary cancer modeling. Sci transl Med. 2011;3(90):90ra59.
82. Mumenthaler SM, Foo J, Leder K, et al. Evolutionary modeling of combination treatment strategies to overcome resistance to tyrosine kinase inhibitors in non-small cell lung cancer. Mol Pharmaceut. 2011;8(6):2069.
83. Zhao B, Sedlak JC, Srinivas R, et al. Exploiting temporal collateral sensitivity in tumor clonal evolution. Cell. 2016;165(1):234-46.
84. Hendriks B, Griffiths G, Benson R, et al. Decreased internalisation of erbB1 mutants in lung cancer is linked with a mechanism conferring sensitivity to gefitinib. Syst Biol (Stevenage). 2006;153(6):457-66.
85. Iadevaia S, Lu Y, Morales FC, et al. Identification of optimal drug combinations targeting cellular networks: integrating phospho-proteomics and computational network analysis. Cancer Res. 2010;70(17):6704-14.
86. Flobak Å, Baudot A, Remy E, et al. Discovery of drug synergies in gastric cancer cells predicted by logical modeling. PLoS Comput Biol. 2015;11(8):e1004426.
87. Ashworth A, Lord CJ, Reis-Filho JS. Genetic interactions in cancer progression and treatment. Cell. 2011;145(1):30-8.
88. Hartwell LH, Szankasi P, Roberts CJ, et al. Friend SH. Integrating genetic approaches into the discovery of anticancer drugs. Science. 1997;278(5340):1064-8.
89. Byrne AB, Weirauch MT, Wong V, et al. A global analysis of genetic interactions in Caenorhabditis elegans. J Biol. 2007;6(3):8.
90. Typas A, Nichols RJ, Siegele DA, et al. High-throughput, quantitative analyses of genetic interactions in E. coli. Nature methods. 2008;5(9):781-7.
91. Jerby-Arnon L, Pfetzer N, Waldman Yedael Y, et al. Predicting Cancer-Specific Vulnerability via Data-Driven Detection of Synthetic Lethality. Cell. 2014;158(5):1199-209.
92. Megchelenbrink W, Katzir R, Lu X, et al. Synthetic dosage lethality in the human metabolic network is highly predictive of tumor growth and cancer patient survival. Proc Natl Acad Sci. 2015;112(39):12217-22.
93. Mellman I, Coukos G, Dranoff G. Cancer immunotherapy comes of age. Nature. 2011;480:480-9.
94. Natarajan M, Lin K-M, Hsueh RC, et al. A global analysis of cross-talk in a mammalian cellular signalling network. Nat Cell Biol. 2006;8(6):571-80.
95. Overall CM, Kleifeld O. Validating matrix metalloproteinases as drug targets and anti-targets for cancer therapy. Nat Rev Cancer. 2006;6(3):227-39.
96. Guex N, Crespo I, Bron S, et al. Angiogenic activity of breast cancer patients’ monocytes reverted by combined use of systems modeling and experimental approaches. PLoS comput Biol. 2015;11(3):e1004050.
97. Yan H, Zhang B, Li S, et al. A formal model for analyzing drug combination effects and its application in TNF-α-induced NFκB pathway. BMC Syst Biol. 2010;4:50.
98. Wang J, Zhang L, Jing C, et al. Multi-scale agent-based modeling on melanoma and its related angiogenesis analysis. Theor Biol Med Model. 2013;10:41.
99. Ji Z, Su J, Wu D, et al. Predicting the impact of combined therapies on myeloma cell growth using a hybrid multi-scale agent-based model. Oncotarget. 2017;8(5):7647-65.
100. Lesterhuis WJ, Bosco A, Millward MJ, et al. Dynamic versus static biomarkers in cancer immune checkpoint blockade: unravelling complexity. Nat Rev Drug Discov. 2017;16(4):264-72.
101. Lesterhuis WJ, Rinaldi C, Jones A, et al. Network analysis of immunotherapy-induced regressing tumours identifies novel synergistic drug combinations. Sci Rep. 2015;5:12298.
102. Sliwoski G, Kothiwale S, Meiler J, et al. Computational Methods in Drug Discovery. Pharmacol Rev. 2014;66(1):334-95.
103. Lafleur K, Huang D, Zhou T, et al. Structure-based optimization of potent and selective inhibitors of the tyrosine kinase erythropoietin producing human hepatocellular carcinoma receptor B4 (EphB4). J Med Chem. 2009;52(20):6433-46.
104. Cerchietti LC, Ghetu AF, Zhu X, et al. A small-molecule inhibitor of BCL6 kills DLBCL cells in vitro and in vivo. Cancer cell. 2010;17(4):400-11.
105. Yang SY. Pharmacophore modeling and applications in drug discovery: challenges and recent advances. Drug Discov Today. 2010;15(11-12):444-50.
106. Cogan D, Aungst R, Breinlinger E, et al. Structure-based design and subsequent optimization of 2-tolyl-(1, 2, 3-triazol-1-yl-4-carboxamide) inhibitors of p38 MAP kinase. Bioorg Med Chem Lett. 2008;18(11):3251-5.
107. Zhang S, Cao Z, Tian H, et al. SKLB1002, a novel potent inhibitor of VEGF receptor 2 signaling, inhibits angiogenesis and tumor growth in vivo. Clin Cancer Res. 2011;17(3):4439-50.
108. Johnson MA, Maggiora GM. Concepts and applications of molecular similarity. 1990:393.
109. Stumpfe D, Ripphausen P, Bajorath J. Virtual compound screening in drug discovery. Future Med Chem. 2012;4(5):593-602.
110. Jamei M, Marciniak S, Feng K, et al. The Simcyp® population-based ADME simulator. Expert Opin Drug Metab toxicol. 2009;5:211-23.
111. Läer S, Elshoff J-P, Meibohm B, et al. Development of a safe and effective pediatric dosing regimen for sotalol based on population pharmacokinetics and pharmacodynamics in children with supraventricular tachycardia. J Am Coll Cardiol. 2005;46(7):1322-30.
112. Nielsen M, Lundegaard C, Lund O, et al. The role of the proteasome in generating cytotoxic T-cell epitopes: insights obtained from improved predictions of proteasomal cleavage. Immunogenetics. 2005;57(1-2):33-41.
113. Larsen MV, Lundegaard C, Lamberth K, et al. Large-scale validation of methods for cytotoxic T-lymphocyte epitope prediction. BMC bioinformatics. 2007;8:424.
114. Nielsen M, Lundegaard C, Worning P, et al. Reliable prediction of T‐cell epitopes using neural networks with novel sequence representations. Protein Sci. 2003;12(5):1007-17.
115. Andreatta M, Nielsen M. Gapped sequence alignment using artificial neural networks: application to the MHC class I system. Bioinformatics. 2015;32(4):511-7.
116. Radunskaya A, de Pillis L, Gallegos A. A Model of Dendritic Cell Therapy for Melanoma. Front Oncol. 2013;3.
117. Kim Y. Regulation of Cell Proliferation and Migration in Glioblastoma: New Therapeutic Approach. Front Oncol. 2013;3.
118. Hawkins-Daarud A, Rockne R, Anderson A, et al. Modeling Tumor-Associated Edema in Gliomas during Anti-Angiogenic Therapy and Its Impact on Imageable Tumor. Front Oncol. 2013;3.
119. Rejniak K, Estrella V, Chen T, et al. The Role of Tumor Tissue Architecture in Treatment Penetration and Efficacy: An Integrative Study. Front Oncol. 2013;3.
120. Aran D, Butte AJ. Digitally deconvolving the tumor microenvironment. Genome Biol. 2016;17(1):175.
121. Siegenthaler C, Gunawan R. Assessment of network inference methods: how to cope with an underdetermined problem. PloS one. 2014;9(3):e90481.
122. Ud-Dean SMM, Heise S, Klamt S, et al. TRaCE+: Ensemble inference of gene regulatory networks from transcriptional expression profiles of gene knock-out experiments. BMC Bioinformatics. 2016;17:252.