Short Communication - Journal of Molecular Oncology Research (2018) Volume 2, Issue 1

Epigenetic carcinogenesis and genetic instability: competitive aspects of the malignant phenotype.

Patrick A Riley^*

Totteridge Institute for Advanced Studies, The Grange, Grange Avenue, London N20 8AB, UK

*Corresponding Author:

Patrick A Riley
Totteridge Institute for Advanced Studies
The Grange, Grange Avenue,
London N20 8AB, UK
E-mail: p.riley@ucl.ac.uk

Accepted date: August 23, 2018

Citation: Riley PA. Epigenetic carcinogenesis and genetic instability: competitive aspects of the malignant phenotype. J Mol Oncol Res. 2018;2(2):42-44.

Abstract

The proposal that carcinogenesis results from the somatic inheritance of defective epigenetic transmission is consistent with the establishment of genetic instability and the generation of a clonally divergent population of cells expressing anomalous structural and functional characteristics. The majority of these uncoordinated properties would be expected to be deleterious, thus placing cancer cells at a proliferative disadvantage. To compensate for this the malignant phenotype requires a property that enables the deviant cells to survive proliferative competition. This question is explored using a competitive growth model based on viewing cell populations as existing in microenvironmental domains subject to a barrier to migration. The model demonstrates that the ability to penetrate this migratory barrier is sufficient to permit otherwise less competitive cells to proliferate and expand the anomalous population. The possible nature of the domain barrier is briefly discussed.

Keywords

Epigenetic, Carcinogenesis, Competition, Domains, Migration

Introduction

One of the difficulties inherent in understanding the process of carcinogenesis is the extraordinary diversity of the properties exhibited by malignant cells. An explanation that appears to make sense is based on the idea that the fundamental lesion in cancer affects the epigenetic transmission of the pattern of genetic expression in different tissues. It has been proposed that the essential mechanism responsible for carcinogenesis is defective vertical transmission of the pattern of gene silencing resulting from cytosine methylation, and its perpetuation by the epigenetic copying of DNA methylation and the associated processes that take place at mitosis of tissue stem cells [1]. The result of faulty copying of epigenetic information is a major disturbance in the pattern of gene expression and modifications to chromosome structure with associated genetic instability of the affected clonal progeny [2].

The proposed derangement of epigenetic gene silencing stipulates a set of cells that, by virtue of their inherited defects, exhibit a high degree of variability in their expressed characteristics resulting in uncoordinated activities and reduced ‘fitness’. These characteristics would be expected to render the affected cells less metabolically efficient with increased loss and a slower proliferation rate. Such characteristics clearly put cancer cells at a competitive disadvantage by comparison with the normal population from which they derive and would be expected to result in the elimination of the abnormal population. A fundamental question about the nature of cancer (malignancy) is the paradoxical triumph of apparently defective cells over normal, metabolically efficient cell populations. An important question is therefore: ‘How do cancer cells survive and prosper given their multiple defects?’

Proliferative Domains

One approach to this problem is to analyse the composition of multicellular organisms as sets of regional populations that occupy local environmental niches or ‘domains’ in which differing classes of cells with different properties are able to coexist in adjacent loci. In such a model the cells are regarded as ecologically identical [3] and coexistence is enabled by limitation of Darwinian competition (i.e. the displacement of less rapidly growing cells by more rapidly proliferating populations) by two factors; one being an altruistic property expressed within domains, and the other the restriction of movement between domains.

Domain Model

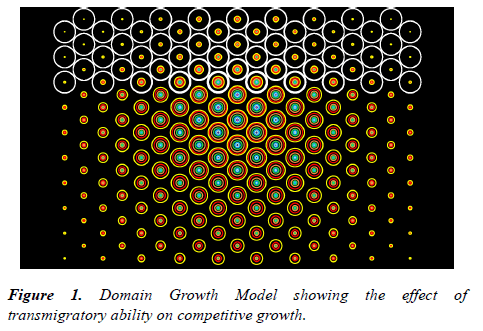
The essence of this approach can be appreciated using a simple 2-dimensional model consisting of a set of adjacent equal domains with space and nutrient supply sufficient to support a limited number of cells. The resource limit is applied as a logistic maximum population (K) and the occupancy of the domain indicated by the area of a circle (Figure 1). The cells within the domain are assigned certain basic properties such as the proliferation rate (r), loss rate (λ), migration rate (m), and an altruistic constant (α).

Competition within Domains

To permit more than one category of cell to coexist in a domain it is necessary to postulate a limitation of proliferative competition to avoid competitive exclusion [4]. This can be achieved by an altruistic factor that dilutes the degree of competition for the limited resources within the domain. Irrespective of the actual mechanism the altruistic process involves a degree of self-inhibition by a population so that its proliferation is more inhibited by competition from its own kind than from a different population. In the model system described this is represented by an altruistic constant (α) with a value greater than unity, giving a growth equation: dN₁/ dt=r₁N₁(1-(α₁N₁+N₂)/K), where α1 is the altruistic constant for population N₁ and N₂ is the coexisting class of cells in a domain with resources sufficient for a total of K cells.

Migration

The model permits migration of cells between domains. This is taken into account by the assumption that cellular exchanges are able to take place between adjacent domains according to a diffusion principle that takes into account the relative cell numbers (i.e. the domain population densities). In the hexagonal arrangement of domains in the scheme described, the exchange of cells is calculated as proportional to the difference between the occupancy of a domain and that of the surrounding six domains. The model enables the exchange to be controlled by setting the migration rate. Setting the migration constant at zero (m=0) assumes the existence of a migratory barrier to the domain and, under these circumstances, the steady-state occupancy for a single population is given by: N=K(1- λ/r), where N is the number of cells and K the logistic limit of the domain.

Barriers to Migration

In the fully developed adult the retention of an architecture embracing cell classes with differing proliferative properties relies on limitation of competition and this is enabled in the model by the effective isolation of domains by interposition of barriers to migration. Thus, for example, a population of nondividing cells occupying a domain adjacent to rapidly growing cells is protected by a boundary to the domain which is impenetrable to the movement of cells.

Cancer and Migration

It can readily be appreciated that cells acquiring the ability to traverse the domain boundaries possess a great potential competitive advantage (For this reason it can be argued, leucocytes need to be non-proliferative).

One can argue, therefore, that a property that would offset the proliferative disadvantage resulting from the metabolic disturbances arising from the deranged genomic expression in cancer cells would be the ability to transgress domain boundaries since competition could be avoided by entry into unoccupied domains. In ecological terms this is constructive niche displacement [5].

The principle is illustrated schematically in Figure 1 which shows a normal population of cells occupying a set of 57 circular domains (shown in white). Arising in a central domain is a competing population. These cells are at a competitive disadvantage in that they have double the loss rate and a proliferation rate that is 25% lower than the resident cells. However, unlike the initial population, the second population of cells is able to migrate between domains and invade unoccupied areas. Their growth is shown by the area of the coloured rings in a linear time sequence indicated in the order: pink/purple/cerise/dark blue/light blue/cyan/green/orange/red/ yellow. The model demonstrates that the ability to invade unoccupied domains enables the growth-disadvantaged population to dominate the system and re-invade the initial domains to the detriment of the initial population.

Figure 1: Domain Growth Model showing the effect of transmigratory ability on competitive growth.

The model suggests that a necessary (and perhaps sufficient) condition for the survival of malignant cell populations is the ability to evade barriers to migration and invade new domains. This could result from re-expression of migratory characteristics exhibited during embryonic development as part of the genetic turmoil emerging from the epigenetic defect.

The Nature of Domain Boundaries

As adumbrated above, territoriality is central to the nature of malignancy. If it is assumed that, in general, all cells are capable of motility the nature of any barrier to migration must reside in failure to form adequate adhesive interactions with the extracellular environment sufficient to permit locomotion. There is evidence that proteoglycans can exert a barrier function. For example, it has been shown that versican acts as a barrier to migration of neural crest cells [6,7]. It appears that proteoglycans interfere with cellular adhesion to extracellular molecules such as fibronectin and laminin which are known to be involved in cell motility. It has been demonstrated that the structural arrangement of chondroitin sulphate polysaccharides in proteoglycans is highly significant in modifying divalent cation binding, with evidence that calcium ions are strongly bound between aligned adjacent sulphate groups [8]. Thus, if tractional adhesions involving integrins are dependent on the availability of divalent cations, the presence of powerful divalent cation chelators in the local extracellular environment would act as effective migratory barriers. There is evidence that cell motility involves integrin binding to extracellular material such as fibronectin, collagen and laminin and that binding to the Arg-Gly-Asp site is influenced by divalent cations such as Mn²⁺, Mg²⁺, and Ca²⁺ [9]. Certainly there is much evidence that barrier tissues contain proteoglycans that act as potent modifiers of cell adhesion and migration [10-14].

The sources of proteoglycans are not clear but if it is further assumed that cells in a non-migratory phase synthesize and secrete barrier proteoglycans it can readily be envisaged that failure to do so will enable emigration to occur. Thus a crucial aspect of the genetic disturbances affecting cancer cells could be the silencing of genes such as HSPG2 or the expression of proteoglycan–degrading enzymes.

Conclusions

The anomalous features of cancer cells that enable them to be diagnosed by cytology are based on a wide range of abnormal morphological properties. According to the epigenetic theory of carcinogenesis these derive from deranged epigenetic control of gene expression and the fundamental lesion of carcinogenesis (at least in adult cancers) is regarded as deranged epigenetic inheritance. This approach is entirely consistent with the evidence that DNA methylation patterns are altered in cancer and also in keeping with the data that show that cancer cells exhibit genetic instability and multiple and varying functional and morphological abnormalities. Since these abnormal features would be expected to put cancer cells at a proliferative disadvantage it is necessary to furnish an explanation for their survival and growth. In the model described here an attempt is made to depict a scenario in which the competitive disadvantage is offset by emigration of malignant cells to microenvironmental niches where proliferative competition is reduced or absent.

Acknowledgements

The microecological domain model of competitive growth was first developed in collaboration with Professor John Vince to whom I am greatly indebted. I also thank Dr Mark Burkitt for helpful discussions and encouragement.

References

1. Riley PA. Epimutation and Cancer: Carcinogenesis Viewed as Error-prone Inheritance of Epigenetic Information. J Oncol. 2018;1-4.
2. Riley PA. Epigenetic Error and Large-scale Genomic Instability in Cancer. Biomed J Sci & Tech Res. 2018;4(3):1-4.
3. Emmel TC (1976) Population Biology. Harper & Row: New York, London.
4. Gause GF (1934). The Struggle for Existence. Macmillan: New York.
5. Pielou EC (1969). An Introduction to Mathematical Ecology. Wiley-Interscience: New York, London.
6. Landolt RM,  Vaughan L,  Winterhalter KH, et al. Versican is selectively expressed in embryonic tissue that act as barriers to neural crest cell migration and axon outgrowth. Development. 1995;121(8):2303-12.
7. Hall BK(2009) The Neural Crest and Neural Crest Cells in Vertebrate Development and Evolution. Springer: New York.
8. Woodward C, Davidson E.A. Structure-function relationship of protein polysaccharide complexes: specific ion-binding properties. Proc Natl Acad Sci USA. 1968;60(1):201-205.
9. Elices MJ, Urry LA, Hemler ME. Receptor functions for the Integrin VLA-3: Fibronectin, collagen, and Laminin Binding are differentially influenced by ARG-GLY-ASP peptide and by divalent cations. J Cell Biol. (1991);112(1):169-81.
10. Ruoslahti E. Proteoglycans in cell regulation. J Biol Chem. (1989);264(23):13369-72.
11. Jackson RL, Busch SJ, Cardin AD. Glycosaminoglycans: Molecular properties, protein interactions, and role in physiological processes. Physiol Rev. (1991);71(2):481-539.
12. Toole BP (1991) Proteoglycans and hyaluranan in morphogenesis and differentiation. In: Cell Biology of Extracellular Matrix. In: Hay ED  (eds.) Plenum Press: New York, pp.305-41.
13. Margolis RK, Margolis RU. Nervous tissue polyglycans. Experientia. (1993);49(5):429-46.
14. Oakley RA, Lasky CJ, Erickson CA, et al. Glycoconjugates mark a transient barrier to neural crest migration in the chicken embryo. Development. (1994);120(1):103-14.