Short Communication - Journal of Applied Mathematics and Statistical Applications (2018) Volume 1, Issue 2

A new approach for solving linear equations with first order through derivatives

*Corresponding Author:

Rami Obeid
Head of data management and analysis division Central bank of Jordan, Jordan
Tel: 962-795-855-036
E-mail: Rami.obeid3@gmail.com

Accepted date: September 17, 2018

Citation: Obeid R. A new approach for solving linear equations with first order through derivatives. J Appl Math Statist Appl. 2018;2(1):8-10.

Abstract

This paper proposes a simple method to solve the first order linear equations, the proposed method is equivalent to classical Cramer’s rule for solving general systems of 2 linear equations, then it describes if there is a relationship between this method and the derivatives. The results show that there is a possible relationship between the method presented in this paper and the derivatives. Furthermore, we can use the first derivative to solve linear equations with first order.

Keywords

Linear equations, Matrix, First derivatives, Cramer’s rule.

Introduction

There are various methods to solve the linear equation, The Cramer's rule is the most common of these methods [1], Klein [2] described the approach based upon Cramer’s rule, the of the linear equation system can be written in matrix form: Ax =b , Cramer’s rule is efficient in solving systems of 2 linear equations. Some recent developments of using Cramer’s rule described in some papers, these papers can be found in [3-5] and the references therein.

Solving linear equations

First, this paper introduces a simple method for solving general systems of 2 linear equations, and we will prove it using Cramer's rule as following:

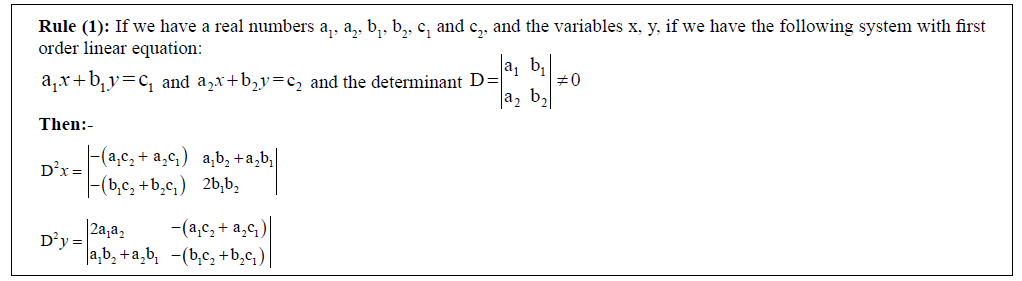
Proof: We can prove the above rule by using Cramer's rule, as we know when we use Cramer's rule we find that:-

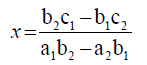(1)

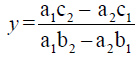and (2)

First, we want to prove that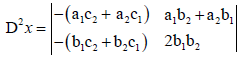

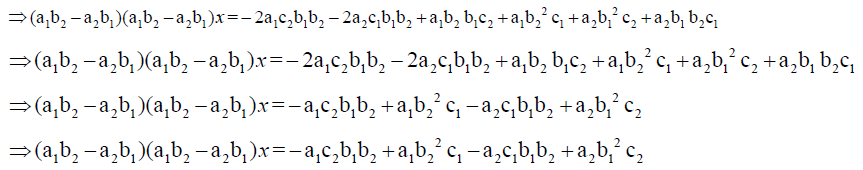
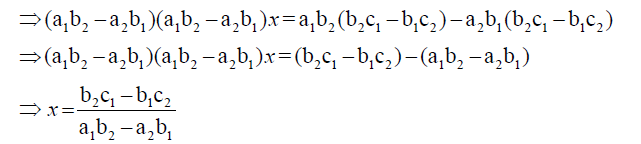
Similarly, we can prove also that 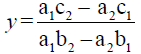by using the above method.

The possible relation between rule 1 and the first derivative: -

Now we will discuss if there is a relation between rule 1 and derivatives: -

Using the same equation in rule (1):-

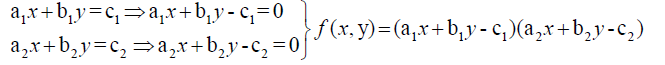
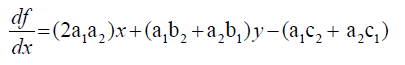
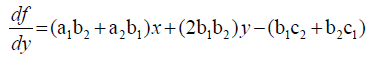
We can represent 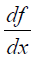and 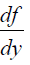by the following matrix:-

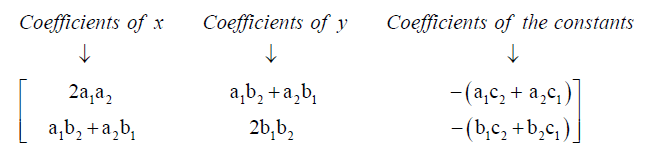
Thus, if we want to find the values of x and y we can easily reach to the same results in Rule 1, where the two columns that we used to find x in rule 1 is similar to the coefficients of the constants and the variable y in the matrix of 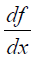respectively:-

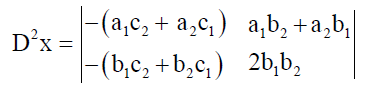
Similarly, the two columns that we used to find y in rule 1 is similar to the coefficients of the variable x and the constants in the matrix of 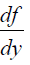respectively: -

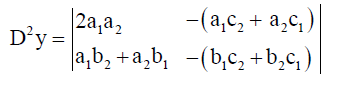
Solving linear equations with first order by first derivatives

To explain how to solve linear equations with first order by first derivatives; suppose we have the following linear equation system: -

x + 2y = 4

3x − y =5

Let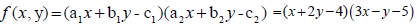

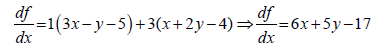
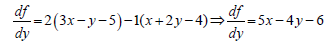
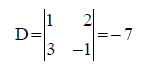
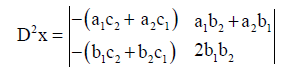
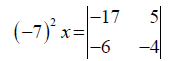
49x =98⇒x = 2

Now to find the value of Y:-

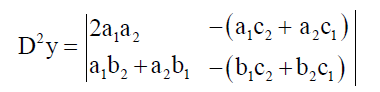
49y = 49⇒y =1

Conclusion

We have studied a simple method for solving systems of 2 linear equations. The method can be easily applied to systems of 2 linear equations. Also, we have described if there is a relationship between this method and the first derivative, the paper show that there is a possible relationship between them, and we can solve linear equations with first order by first derivatives.

References

1. Cramer G. Introduction l?Analyse des lignes Courbes algbriques. Geneva: Europeana. 1750; pp 656-9.
2. Klein RE. Teaching linear systems theory using Cramer?s rule. IEEE Transactions on Education, 1990; 33:258-67.
3. Diaz-Toca GM, Vega GL, Lombardi H. Generalizing Cramer?s Rule: Solving Uniformly Linear Systems of Equations. SIAM J. Matrix Anal. & Appl. 2005; 27:621-37.
4. Habgood K, Arel I. A condensation-based application of Cramer?s rule for solving large-scale linear systems. J Discrete Algorithms. 2012; 10: 98-109.
5. Kyrchei II. Cramer?s rule for quaternionic systems of linear equations. Journal of Mathematical Sciences. 2008; 155:839-58.