Research Paper - Journal of Chemical Technology and Applications (2018) Volume 2, Issue 1

A compact, algebraic formulation of disproportionation and symproportionation in Bromine systems.

*Corresponding Author:

Tadeusz Micha?owski
Department of Oncology The University Hospital in Cracow 31-501 Cracow, Poland
Tel: +212667845404
E-mail: michalot@o2.pl

Accepted date: July 03, 2018

Citation: Michalowska-Kaczmarczyk AM, Michalowski T. A compact, algebraic formulation of disproportionation and symproportionation in Bromine systems. J Chem Tech App. 2018;2(2):1-14.

Abstract

Numerous examples of disproportionation and symproportionation of bromine in dynamic redox systems are resolved according to GATES/GEB principles and represented graphically by the functions E = E(Φ) and pH = pH(Φ) of the fraction titrated Φ, and completed by dynamic speciation diagrams log zi ( ) i i log ??X ?? = ? Φ , for different species zi i X . The results of calculations can be considered from the viewpoint of relative efficiency of the competing reactions, on different steps of the titration procedure. The idea of linear combination of the balances related to electrolytic systems (aqueous media) is presented in context of GEB formulation GEB according to Approach II. Oxidation number, oxidant, reductant, are perceived as derivative (not primary) concepts within GATES/GEB. The equivalency of Approaches I and II to GEB is also proved.

Keywords

Thermodynamics of electrolytic redox systems, GEB, GATES/GEB, disproportionation, symproportionation, Potentiometric titration.

Notations: GATES: Generalized Approach to Electrolytic Systems; GEB: Generalized Electron Balance; ON: Oxidation Number

Introduction

Disproportionation [1] and symproportionation [2] are two mutually opposite phenomena classified as redox reactions. We will focus here our interest on aqueous solutions as electrolytic redox systems, of which physicochemical knowledge is relatively extensive.

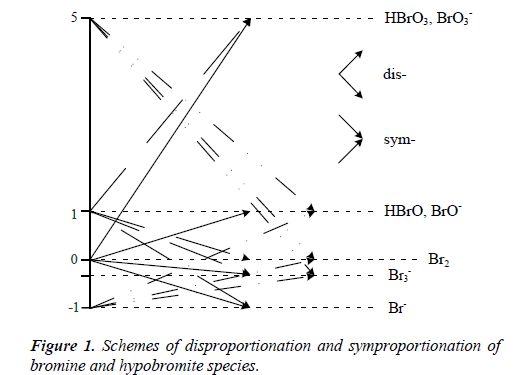
Disproportionation is a special type of redox reaction, where an element on an intermediate oxidation number (ON) in a species is transformed – simultaneously – to the species with lower and higher ONs of this element. It means that this element must be able to form the species with at least three different oxidation numbers (ONs). For example, bromine forms the species with five ONs (–1, –1/3, 0, 1, 5) (Figure 1). In Br₂ and BrO^-1, bromine has intermediate ONs: 0 and 1, resp. In particular, the disproportionation of Br₂, affected by OH^-1 ions, can be written as follows [3]:

Figure 1: Schemes of disproportionation and symproportionation of bromine and hypobromite species.

3Br₂ + 6OH-1 = BrO₃-1 + 5Br^-1 + 3H₂O (1a)

Br₂ + 2OH-1 = BrO^-1 + Br^-1 + H₂O (1b)

etc. In the symproportionation, two reactants containing the same element, here: Br with different ONs, react with formation of the species on intermediate ONs of this element (Figure 1). For example, symproportionation of BrO₃-1 and Br^-1, affected by H⁺¹ ions, can be written as follows:

BrO₃-1 + 5Br^-1 + 6H⁺¹ = 3Br₂ + 3H₂O (2a)

BrO₃-1 + 8Br^-1 + 6H⁺¹ = 3Br₃-1 + 3H₂O 2(b)

etc.

A remark. The disproportionation reactions in biological systems are termed as dismutation, when associated with superoxide dismutases (SODs) – the enzymes catalysing a dismutation of toxic superoxide (O₂⁻¹) radical [4]. In French, the term dismutation refers also to non-biological systems [5]. Comproportionation [6] and synproportionation [7]), as the synonyms of symproportionation, are also found in literature.

The disproportionation may be affected by an action of the solvent, e.g. dilution with water, to which the bromine compound at an intermediate oxidation state, e.g. HBrO, has been introduced. The disproportionation effect can be greatly enhanced by the action of an acid or base. In some instances, it can also be stated that the disproportionating agent acts also as an oxidant or reductant [3]. In a particular case, namely in reaction Br₂ + Br^-1 = Br₃^-1, the symproportionation is indistinguishable from the complexation effect.

The redox systems are formulated, from thermodynamic viewpoint, according to Generalized Approach to Electrolytic Systems (GATES) [8,9] principles, formulated by Michałowski. For this purpose, the set of K algebraic equations, f₀,f₁₂,f₃,…,f_K, is formulated. It is composed of: charge balance (ChB, f₀), the linear combination f₁₂ = 2∙f₂ – f₁, of elemental balances: f₁ = f(H) for H and f₂ = f(O) for O, and K–2 elemental/core balances f(Y_k) (k=3,…,K) for elements/cores Y_k (≠ H, O). The f₁₂ is the primary form of the Generalized Electron Balance (GEB), discovered by Michałowski, and formulated as the Approach II to GEB [3,8-24]. The GATES related to redox systems will be denoted as GATES/GEB. The GATES is related to redox and non-redox systems, and then GATES/GEB ⊂ GATES.

Another option is the Approach I to GEB [25-28], discovered by Michałowski, and considered later as the ‘short’ version of GEB. The Approach I to GEB is based on a ‘card game’ principle, with electron-active elements as ‘players’, electronnon- active elements as ‘fans’, and electrons as ‘money’ [22]. The equivalency of Approaches I and II to GEB will be proved, and then the balances for GEB be formulated for different systems according to the Approach I.

All attainable physicochemical knowledge can be involved in further, numerical calculations, realized with use of an iterative computer program. The results of calculations are presented graphically and discussed. The GATES/GEB is perceived as the best tool for thermodynamic resolution of electrolytic redox systems, according to algebraic principles.

Thermodynamic modelling of redox systems

Modelling of electrolytic redox systems according to GATES/ GEB principles is based on general laws of elements and charge preservation, related to closed systems composed of condensed phases, separated from the environment by diathermal walls. In further discussion, we refer to redox systems formed in aqueous media, where the species are perceived in their natural form, as hydrates , where z_i (z_i = 0, ±1, ±2,…) is the external charge of expressed in elementary charge unit e = F/N_A (F – Faraday constant, N_A – Avogadro’s constant), and niW (≥ 0) is the mean number of water (W = H₂O) molecules attached to

Components and species: The terms: components and species are distinguished. Components form a system, the species are present in the system thus formed. A static system is obtained after disposable mixing the components: H₂O as solvent, and solute(s). A dynamic D+T system is a result of addition of titrant T into titrand D, in consecutive portions. The D and T are composed separately before the titration, where the D+T mixture is formed; the D and T are subsystems of the D+T system. A volume V mL of T is added into V₀ mL of D, up to a given point of the titration, and V₀+V mL of D+T mixture is thus obtained, if the assumption of the volumes additivity is valid/ tolerable. In the notation applied here, N_0j (j=1,2,…,J) is the number of molecules of the component of j-th kind, including water, forming D and T in dynamic D+T system. The D+T system thus obtained involves N₁ molecules of H₂O ( = H₂O, z₁=0) and Ni species of i-th kind, (i=2,3,…,I), denoted briefly as 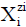(N_i ,n_i) where n_i≡n_iW≡n_iH₂O.

The known chemical formulas of 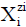and their respective charges provide the information necessary/sufficient to formulate the respective balances, for elements or cores. A core is a cluster of elements with defined composition, structure and external charge that remains unchanged in a system considered.

Formulation of balances: general remarks: It is advisable to start the balancing from the interrelations between numbers of particular entities: N_0j for components represented by molecules composing D and T, and N_i – for the species (ions and molecules) of i-th kind (i = 1,…,I), where I is the number of kinds of the species in D+T. 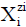The mono- or two-phase electrolytic D+T system thus obtained involve N₁ molecules of H₂O and Ni species of i-th kind, (i=2,3,…,I), specified briefly as (N_i ,n_i) ,where n_i ≡n_iW ≡n_iH₂O is the mean number of hydrating water molecules (W=H₂O) attached to 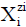.The net charge of equals to the charge of 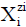, i.e., z_i + n_iW∙0 = z_i.For ordering purposes, we write the sequence: H⁺¹ (N₂, n₂), OH^-1 (N₃, n₃), … , i.e., z₂ = 1, z₃ = –1, … . The 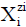's, with different numbers of H₂O molecules involved in , e.g. {H⁺¹, H₃O⁺¹,H₉O₄⁺¹}, {H₄IO₆^-1, IO₄^-1} are considered equivalently, i.e., as the same species in this medium. The charge of a species , expressed in elementary charge units, results from the numbers of protons in nuclei, and orbital electrons in atoms composing the species.

Presentation of the species in natural forms in aqueous media, i.e., as , has several advantages. This way, after linear combinations of the related balances, one can discover some regularities hidden earlier by notation of the species in the form 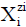This notation can be extended on electrolytic systems in mixed-solvent A_s (s=1,…,S) media, where mixed solvates 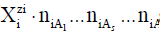are assumed, and 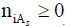is the mean numbers of A_s (s=1,…,S) molecules attached to 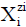[15,21,29]. 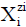In other instances (reaction notation), the common/simpler notation of the species, e.g. HSO₄^-1∙ n₄H₂O as HSO₄^-1, will be practiced. Molar concentrations [mol/L] of the species be denoted as 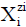, for brevity.

The notation of the species is useful on the step of formulation of the related balances: charge balance (f₀ = ChB) and elemental balances, f_k = f(Y_k), in the system where K elements Y_k (k=1,…,K) are involved. The ChB expresses the electroneutrality of the electrolytic system, whereas the f(Y_k), (k=1,…,K) express the conservation of all the elements in the closed system, chosen for modelling purposes. For simplicity/ uniformity of notation, we assume the sequence: f₁ = f(H), f₂ = f(O),… ,f_k= f(Y_k).

The charged/ionic species of the system, i.e., the species with z_i ≠ 0 (z_i > 0 for cations, z_i < 0 for anions), are involved in the charge balance

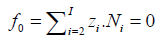(3)

Free water particles, and water bound in the hydrates are included in the balances: f₁ = f(H), f₂ = f(O):

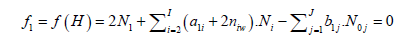(4)

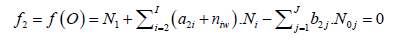(5)

Then the balance

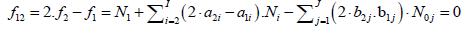(6)

is formulated.

The elemental balances: f₃,...,f_K , interrelating the numbers of atoms Y_k ≠ H, O in components and species, are as follows

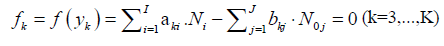(7)

where a_ki and b_kj in equations 4, 5 and 7 are the numbers of element Y_k (k=1,...,K) in , and in the j-th component of the system, resp.

The linear combination

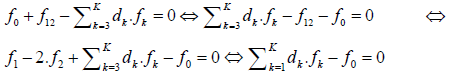(8)

involves K balances: f₀, f₁₂, f₃ ,…,f_K. In particular, d₁ = +1, d₂ = –2. As will be indicated below, when the multipliers dk are equal to (or involved with) the oxidation numbers (ON’s) of the corresponding elements E_k (k=1,…,K) in a redox system, we get the simplest (most desired) form of the related linear combination (eq. 8), as will be explained on the example presented in section 3.5.

In eq. 6 and then in eq. 8, the terms involved with water, i.e., N₁, N_0j (for j related to H₂O as the component), and all n_i = n_iW are not involved. The necessity of prior knowledge of niW values in the balancing is thus avoided. The n_i = n_iW = niH₂O values are virtually unknown – even for X₂^z2 = H⁺¹ [30] in aqueous media, and depend on ionic strength (I) of the solution.

For a redox system, (f₀, f₁₂, f₃ ,…,f_K) is the set of K independent, algebraic equations. The f₁₂ is the primary form of Generalized Electron Balance (GEB), f₁₂ = pr-GEB [12,17]. All the balances thus obtained are expressed in terms of concentrations, see Table 1 in context of Table 2. The charge balance has there the form

Table 1: Composition of titrand D and titrant T in the systems S1,?,S11.

Table 2: (S1,S2). The sets of (?, ph, E) values taken from the vicinity of the equivalence points, at (C₀,V₀,C) = (0.01,100,0.1).

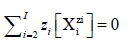(3a)

Note that [ X_m] = 0 for a species m mw X_m.n_mw with zero charge (z_m=0), e.g., 0∙[H₂O] = 0 (z₁=0).

The term charge balance (ChB) is used for both forms of this relation, e.g., for ChB expressed by equations: 3 (in terms of N_i, N_0j), and 3a (in terms of concentrations); it is done in accordance with the ‘Ockham razor’ principle. This conceptual ‘abuse’ should not lead to ambiguities, in the right context. In addition, the term GEB will be applied both to f₁₂, and to the linear combinations, expressed by eq. 8 (in terms of N_i, N_0j), and to the related balances written in terms of concentrations. The elemental/core balances expressed in terms of concentrations are named as concentration balances, for Y_k ≠ H, O (k=3,…,K). The balances expressed in terms of concentrations are compatible with expressions for equilibrium constants, specified in Table 3. Consequently, the system of balances related to a redox system consists of three types of balances, expressed in terms of concentrations: GEB, ChB, and K–2 concentration balances for the related elements/cores Y_k ≠ H, O; k= 3,…,K. For modelling purposes, the balances are related to the closed system, separated from the environment by diathermal walls [22].

Table 3: Supplementary computational data for the systems S1 and S2.

As indicated elsewhere [31], for a non-redox system, the equation 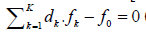(eq. 8) is transformed into identity, 0 = 0, and then f₁₂ is not an independent equation. Consequently, in non-redox systems, f₁₂ is the equation dependent on f₀,f₃,…,f_K, and 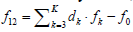. In other words, f₀,f₃,…,f_K is the set of K – 1 independent equations for a non-redox system. For non-redox systems, f₀,f₃,…,f_K is transformed into charge balance (eq. 3a) and K – 2 concentration balances for Y_k ≠ H, O. In other words, f1, f2 and f12 are not formulated for non-redox systems. The dependency or independency of f12 from the balances f₀,f₃,…,f_K is the general criterion distinguishing between non-redox and redox systems [11].

Formulation of the proper (i.e., with dk equal to ON’s) linear combinations is applicable to check the linear dependency or independency of the balances. This way is realized a very useful/ effective manner for checking/stating the linear dependence of the balances: f₀, f₁₂, f₃ ,…,f_K related to non-redox systems, named as the transformation of the linear combination (6) to the identity, 0 = 0 [12]. For this purpose, in all instances, we try to obtain the simplest form of the linear combination (6).

Let us repeat: For a redox system, the proper linear combination (6), with d_k equal to ON’s, is the way towards the simplest/ shortest form of GEB; for a non-redox system, it is the way towards identity, 0 = 0.

To avoid possible/simple mistakes in the realization of the linear combination procedure, we apply the equivalent relations:

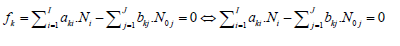(9)

for elements with negative oxidation numbers, or

(10)

for elements with positive oxidation numbers, k ∈ 3,…,K. In this notation, f_k will be essentially treated not as the algebraic expression on the left side of the equation fk = 0, but as an equation that can be expressed in alternative forms presented above.

Note, for example, that 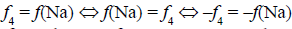. The change of places of numbers N_i for components and N_0j for species (see equations 9, 10) facilitates the purposeful linear combination of the balances, and enables to avoid simple mistakes in this operation.

Concentrations of solutes in D and T of D+T redox systems S1 – S11 considered in this paper are specified in Table 1 (columns 2, 3). The set of balances for a particular redox system, specified in rows of Table 1, consists of: generalized electron balance (GEB, column 4), charge balance (ChB, column 5) and concentration balance(s) (column 6). The symbols used in columns 4,5,6 of Table 1 and further notations are as follows:

C₀ – concentration of analyte (A) in D, C₀₁ – concentration of H₂SO₄ in D, C – concentration of reagent (B) in T;

u = V/(V₀+V); u₀ = V₀/(V₀+V);

β = C∙u, β₀= C0∙u₀, β₀₁ = C₀₁∙u₀ ;

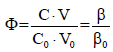– fraction titrated ;

Atomic number Z_Br=35 for Br;

Molar concentration 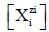of the species in the D+T mixture is involved in the relation

;

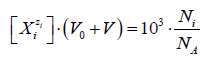α = [H⁺¹] – [OH^-1] = 10^-pH – 10^pH-14 ;

ϑ₀ = RT/F∙lN₁₀ – Nernstian slope; ϑ₀ = 0.05916 V at T = 298 K;A = 1/0.05916 = 16.9;

P_1Br = (Z_Br–5)([HBrO₃]+[BrO₃^-1]) + (Z_Br–1)([HBrO]+[BrO^-1]) + 2Z_Br[Br₂] + (3Z_Br+1)[Br₃^-1] + (Z_Br+1)[Br^-1];

P_2Br = [BrO₃^-1] + [BrO^-1] + [Br₃^-1] + [Br^-1];

P_3Br = [HBrO₃] + [BrO₃^-1] + [HBrO] + [BrO^-1] + 2[Br₂] + 3[Br₃^-1]+ [B_r^-1];

P_2S = [HSO₄^-1] + 2[SO₄^-2] ; P_3S = [HSO₄^-1] + [SO₄^-2].

All concentrations of components and species involved with notation applied in Table 1 are expressed in mol/L, and all volumes – in mL. In this notation, common segments of the related balances are distinguished; it allows to simplify the extensive formulation, and may be helpful in construction of the appropriate algorithms. Numerical values of equilibrium constants needed/used in the calculations are involved in the relations:

[H⁺¹] = 10^-pH ; [OH^-1] = 10^pH-14 ; [HSO₄^-1] = 10^1.8-pH[SO₄^-2]; n b

[Br₂] = 10^{2A(E-1.087)-2pBr} ; [Br₃^-1] = 10^{2A(E-1.05)-2pBr} ; [BrO^-1] = 10^{2A(E-0.76)-pBr+2pH-28} ;

[HBrO] = 10^8.6-pH∙[BrO^-1] ; [BrO₃^-1] = 10^{6A(E-1.45)-pBr+6pH} ; [HBrO₃] = 10^0.7-pH∙[BrO₃^-1];

As stated above, formulation of GEB can be realized according to Approaches I or II to GEB; both Approaches are equivalent, i.e.,

Approach I to GEB Approach II to GEB (11)

A remark: The GEB concept is quite different from the ‘electron balancing’ procedure applied in laying the redox reactions according to stoichiometric ‘rules’, criticized extensively in [8,18,19,32-34]; it is also different from the term ‘electron balance’ applied for description of: microbial metabolism [35], electrons in light-emitting diodes [36], etc., and… from ‘electronic balance’, as the device for mass measurement [37].

Formulation of the system S1

Preliminary data: Formulation of GEB according to both Approaches (I and II) to GEB will be exemplified first by the system S1 in Table 1, formed from D and T, considered as subsystems of the D+T system. V₀ mL of D is composed of Br₂ (N₀₁ molecules) + H₂O (N₀₂molecules), and V mL of T is composed of NaOH (N₀₃ molecules) + H₂O (N₀₄ molecules). In the D+T system we have I = 11 species:

H₂O (N₁), H⁺1 (N₂,n₂), OH^-1 (N₃,n₃), HBrO₃ (N₄,n₄), BrO₃^-1 (N₅,n₅), HBrO (N₆,n₆), BrO^-1 (N₇,n₇), Br₂ (N₈,n₈),

Br₃^-1 (N₉,n₉), Br^-1 (N₁₀,n₁₀), Na⁺¹ (N₁₁,n₁₁) (12)

Note, for example, that N₄ molecules of HBrO₃∙n₄H₂O (z₄=0) involve: N₄(1+2n₄) atoms of H, N₄(3+n₄ ) atoms of O, and N₄ atoms of Br.

The species formed from Br₂ and H₂O in D, and then present in D+T, resulted from hydrolytic disproportionation: 3Br₂ + 3H₂O = BrO₃^-1 + 5Br^-1 + 6H⁺¹; 3Br₂ + 3H₂O = HBrO₃ + 5Br^-1 + 5H⁺¹; Br₂ + H₂O = HBrO + Br^-1 + H⁺¹; Br₂ + H₂O = BrO^-1 + Br^-1 + 2H⁺¹. The symproportionation reaction Br₂ + Br^-1 = Br₃ -1 can be also perceived as complexation. The ONs for H, O and Na are not changed, i.e., these elements are not oxidized or reduced.

Approach I to GEB in S1: The Approach I to GEB needs prior knowledge of ON’s for all elements in components and species of the system in question. In S1, one element (Br) is considered a priori as the only one electron-active element (player); K*=1 is here the number of players.

In the system S1, bromine (as Br₂) is the carrier/distributor of its own, bromine electrons. One atom of Br has Z_Br bromine electrons, and then one molecule of Br₂ has 2Z_Br bromine electrons, i.e., N0₁ molecules of Br₂ involve 2Z_Br∙N0₁ bromine electrons. The oxidation degree x of an atom in a simple species, such as ones formed here by bromine, is calculated on the basis of known oxidation degrees: +1 for H, and –2 for O, and external charge of this species. We have, by turns, the relations: 1∙1 + 1∙x + 3∙(–2) = 0 → x= 5 for HBrO₃; 1∙x + 3∙(–2) = –1 → x = 5 for BrO₃^-1; 1∙1 + 1∙x + 1∙(–2) = 0 → x = 1 for HBrO;…; 3∙x = –1 → x = –1/3; 1∙x = –1 → x = –1 for Br^-1.

The oxidation degree is the net charge resulting from the presence of charge carriers, inherently involved in an atom: protons in nuclei and orbital electrons, expressed in elementary charge units as: +1 for protons, and –1 for electrons. The number y of bromine electrons in one molecule of HBrO₃ is calculated from the formula: Z_Br∙(+1) + y∙(–1) = 5, i.e., bromine involves y = Z Br–5 bromine electrons, etc. On this basis, we state that [22,38]:

N₄ species HBrO₃∙N₄H₂O involve (Z_Br–5)∙N₄ bromine electrons;

N₅ species BrO₃^-1∙N₅H₂O involve (Z_Br–5)∙N₅ bromine electrons;

N₆ species HBrO∙N₆H₂O involve (Z_Br–1)∙N₆ bromine electrons;

N₇ species BrO^-1∙N₇H₂O involve (Z_Br–1)∙N₇ bromine electrons;

N₈ species Br₂∙N₈H₂O involve 2Z_Br∙N₈ bromine electrons;

N₉ species Br₃ -1∙N₉H₂O involve (3Z_Br+1)∙N₉ bromine electrons;

N₁₀ species Br^-1∙N₁₀H₂O involve (Z_Br+1)∙N₁₀ bromine electrons;

The N0₁ molecules of Br₂ involved 2Z_Br∙N0₁ bromine electrons. These (bromine) electrons were dissipated between different bromine species, indicated above. The balance for the bromine electrons is then as follows:

2Z_Br∙N0₁ = (Z_Br–5)∙N₄ + (Z_Br–5)∙N₅ + (Z_Br–1)∙N₆ + (Z_Br–1)∙N₇ + 2Z_Br∙N₈ + (3Z_Br+1)∙N₉ + (Z_Br+1)∙N₁₀ (13)

Applying in (13) the relations:

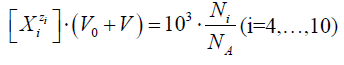and

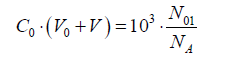(14)

we get

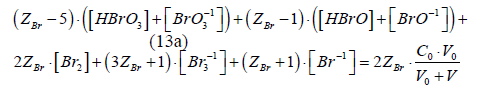
Eq. 13a is the GEB for S1, obtained according to the Approach I to GEB. Applying the notation from Table 2, from eq. 13a we get the balance P_1Br = 2Z_Br∙β₀, identical with the one specified in column 4 for S1.

Approach II to GEB in S1: The balances related to the D+T mixture are as follows:

f₀ = ChB

N₂ – N₃ – N₅ – N₇ – N₉ – N₁₀ + N₁₁ = 0 (15)

f₁ = f(H)

2N₁ + N₂(1+2n₂) + N₃(1+2n₃) + N₄(1+2n₄) + 2N₅n₅ + N₆(1+2n₆) + 2N₇n₇ + 2N₈n₈ + 2N₉n₉ +

2N₁₀n₁₀ + 2N₁₁n₁₁ = 2N₀₂ + N₀₃ + 2N₀₄ (16)

f₂ = f(O)

N₁ + N₂n₂ + N₃(1+n₃) + N₄(3+n₄) + N₅(3+n₅) + N₆(1+n₆) + N₇(1+n₇) + N₈n₈ + N₉n₉ + N₁₀n₁₀ + N₁₁n₁₁

= N₀₂ + N₀₃ + N₀₄ (17)

– f₃ = – f(Na)

N₀₃ = N₁₁ (18)

f₄ = f(Br)

N₄ + N₅ + N₆ + N₇ + 2N₈ + 3N₉ + N₁₀ = 2N₀₁ (19)

From Equations 16 and 17 we have

f₁₂ = 2∙f₂– f₁ :

– N₂+ N₃ + 5N₄ + 6N₅ + N₆ + 2N₇ = N₀₃ (20)

From equations 15, 18 and 20 we have

f₁₂ + f₀ – f₃ :

5N₄ + 5N₅ + N₆ + N₇ – N₉ – N₁₀ = 0 (21)

Applying the atomic number Z_Br for Br, from Equations 19 and 21 we obtain the equation

Z_Br∙f₄ – (f₁₂ + f₀ – f₃) :

(Z_Br– 5)(N₄+N₅) + (Z_Br– 1)(N₆+N₇) + 2Z_BrN₈ + (3Z_Br+1)N₉ + (Z_Br+1)N₁₀ = 2Z_BrN₀₁

identical with eq. 13. This way, the equivalency of the Approaches I and II (eq. 11) is proved for the system S1.

In the balance f₁₂ = 2∙f₂ – f₁ = 2∙f(O) – f(H) (eq. 20), the numbers of water molecules: N₁, n_iW, and those N_0j related to H₂O as component/solvent (here: N₀₂ and N₀₄) used for preparation of D and T are cancelled. In other systems, also hydrating water molecules introduced by some components (e.g. CuSO₄∙5H₂O in [20]), are also cancelled within f₁₂.

Charge and concentration balances for S1: From equations 14, 15, 18, 19 and Tables 1 and 2 we have

[H⁺¹] – [OH^-1] – [BrO₃^-1] – [BrO^-1] – [Br₃^-1] – [Br^-1] + [Na⁺¹] = 0

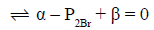(15a)

(18a)

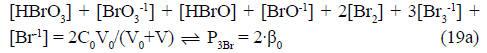
Eq. 19a is the concentration balance for Br, see column 6 in Table 1 for S1. Note that α, P_2Br and β are considered as segments of eq. 15a, applied also in balances related to other systems specified in Table 1.

Other/equivalent forms of GEB in S1: Note that the GEB for the system S1, obtained from f₁₂ (eq. 20), has the form

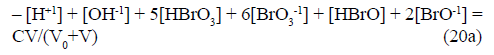
From eq. 21 we have

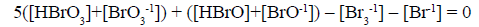(21a)

Other combinations of f12 (eq. 20) with f₀, f₃ and f₄ (equations 15,18,19) have also full properties of GEB for the system S1. Among others, we have

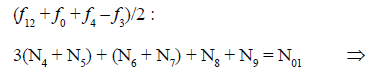(22)

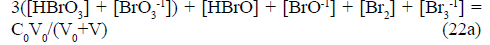
Equations 21a and 22a can be perceived as the steps towards the shortest (involving the smallest number of terms) form of GEB in S1. Summarizing, the equations 13a, 20a, 21a and 22a are the equivalent forms of GEB in the system S1.

Computer program for the system S1: Some of the balances specified above are involved in the set of independent balances applied in the computer program.

function F = NaOH_Br2(x)

global V C0 V0 C yy

E = x(1);

pH = x(2);

pBr = x(3);

H = 10^(-pH);

Kw = 10^-14;

pKw = 14;

OH = Kw/H;

A = 16.9;

Br = 10^-pBr;

ZBr = 35;

Br2=Br^2*10^(2*A*(E-1.087));

Br3=Br^3*10^(2*A*(E-1.05));

BrO=Br*10^(2*A*(E-0.76)+2*pH-2*pKw);

BrO3=Br*10^(6*A*(E-1.45)+6*pH);

HBrO = 10^8.6*H*BrO;

HBrO3=10^0.7*H*BrO3;

Na=C*V/(V0+V);

F = [%Charge balance

(H-OH -Br-Br3-BrO-BrO3+Na);

%Concentration balance for Br

(Br+3*Br3+2*Br2+HBrO+BrO+HBrO3+BrO3-2*C0*V0/ (V0+V));

%Electron balance

( ( Z B r + 1 ) * B r + ( 3 * Z B r + 1 ) * B r 3 + 2 * Z B r * B r 2 + ( Z B r - 1)*(HBrO+BrO)...

+(ZBr-5)*(HBrO3+BrO3)-2*ZBr*C0*V0/(V0+V))];

yy(1)=log10(Br);

yy(2)=log10(Br3);

yy(3)=log10(Br2);

yy(4)=log10(HBrO);

yy(5)=log10(BrO);

yy(6)=log10(HBrO3);

yy(7)=log10(BrO3);

yy(8)=log10(Na);

end

The calculation procedure is realized according to an iterative computer program, here: MATLAB [8]. The volume V of the titrant (T) added is the parameter. In this program, the set of 3 independent variables, forming a (transposed) vector is considered. The number of the (independent, ‘homogeneous’) variables is equal to the number of equations; this ensures a unique solution of the equations related to the system S1, at the pre-set C0, C and V0 values, and the V-value at which the calculations are realized, at defined step of the calculation procedure. The set of equations {15a, 19a, 13a}, involving GEB, obtained according to Approach I to GEB, was applied there. The set of independent equations: {15a, 19a, 20a}, {15a, 19a, 21a} or {15a, 19a, 22a} can be chosen, optionally, for this purpose. The complete set of interrelations between concentrations of the species in the balances, taken from Table 3, is applied.

x^T = (x(1), x(2), x(3)) = (E, pH, pBr) (23)

The ‘homogeneity’ of the variables in (23) results from the fact that all them are found in the exponents of the power for 10 in: [e^-1] = 10^-A∙E, [H⁺¹] = 10^-pH, [Br^-1] = 10^-pBr, where A = 16.9 at T = 298 K (Table 2).

In the computer program, two measurable variables: potential E and pH are involved in the set (23). The E values are related here to the normal hydrogen electrode (NHE) scale. In all cases presented in this paper, the curves E = E(Φ), pH = pH(Φ) and speciation diagrams with the curves zi log [X_i^zi] vs. Φ are plotted.

Equations and equalities in S1: Among the concentration balances for the systems specified in Table 1, one can distinguish equations and equalities. In the system S1, we have an equality, represented by the balance 18a, which involves only one species (here: Na⁺¹). In the equality 18a, the value for [Na⁺¹] is a number (not variable) for the pre-assumed C and V0 values, at given V-value; as such, it can enter immediately the related ChB, column 5 for S1 in Table 1. Other balances, here: 13a, 15a and 19a, involve more species, and then are classified as equations. Then (18a) is not considered as equation, if the number of equations be compared with the number of independent variables, here: 3 = 3.

Oxidation number, oxidant and reductant as the redundant terms in S1: The GEB related to the system S1, and expressed by eq. 21a, obtained according to Approach II to GEB, can be rewritten as follows:

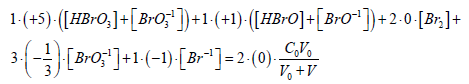(21b)

As we see, the balance (21b), obtained from f₁₂ + f₀ – f₃, i.e., from the linear combination of f₀ and balances for ‘fans’ (H, O, Na), has the oxidation numbers (ON) of Br in its species equal to (or involved with) the coefficient/multiplier at the concentration of the Br-species, and at concentration of the Br-component (here: Br₂). If the species or component involves more Br-atoms, e.g., Br₃^-1, then we have 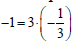, i.e. the product of the number of Br-atoms, and the ON for Br in Br₃^-1.

This regularity can be extended on other redox systems. Concluding, the formulation of GEB according to Approach II to GEB

• needs none prior knowledge of ON’s for elements participating the redox system; it means that ON is the derivative concept within GATES/GEB;

• the terms: oxidant and reductant (as distinguisher, attribute, differentia specifica) are not assigned a priori to individual components and species of the redox system; there is simply no need for this, i.e., full ‘democracy’ in this respect is assumed.

In this context, the linear combination f₁₂ + f₀ – f₃ and the resulting eq. 21b exemplify the ‘purposeful’ linear combination.

Completeness/redundancy/compatibility of equilibrium constants: The preparatory step in the formulation of redox systems according to GATES/GEB principles involves gathering of the corresponding equilibrium data, i.e., the standard potentials E0’s, and other equilibrium constants (Table 3). The set of equilibrium constants should be complete, as far as possible. The point is that these sets of data, often presented in the corresponding tables of equilibrium constants, are usually incomplete and/or refer to different equations of the related reactions. The related equilibrium constants can be obtained from other equilibrium constants, as were shown in [12,28], where the problem of redundancy and compatibility was considered in context with the system S1. The problem of redundancy is involved with seemingly excessive number of physicochemical data, collected from various thematic studies, or different works.

Disproportionation in dynamic bromine systems

In algorithms applied for all dynamic systems S1 – S6, specified in Table 1 and presented below, it is assumed that V₀ = 100, C₀ = 0.01, C = 0.1. All the systems will be illustrated graphically, on the graphs (a) E = E(Φ), (b) pH = pH(Φ) and (c) log [X_i^zi] =ϕ (Φ) plotted as the functions of the fraction titrated

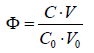(24)

It provides a kind of normalization in the related graphs, i.e., independency on V₀ value. In principle, C₀ is related to an analyte (A), and C – to a reagent B for this analyte (Tables 1 and 2). Some dynamic systems are presented in extended, graphical forms.

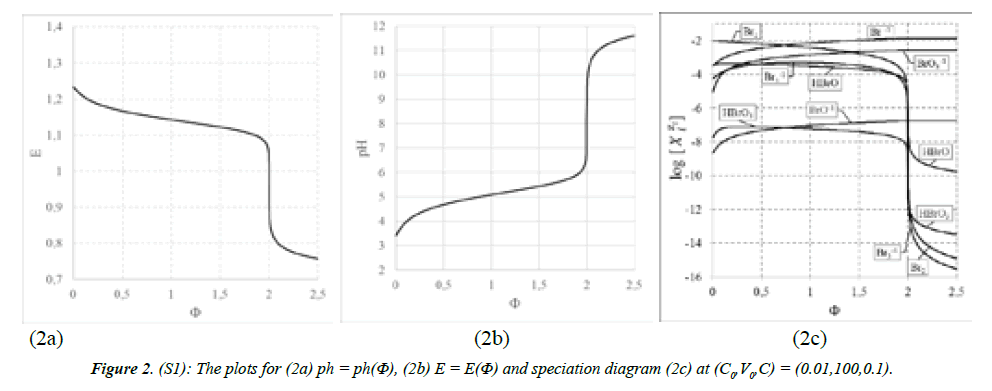
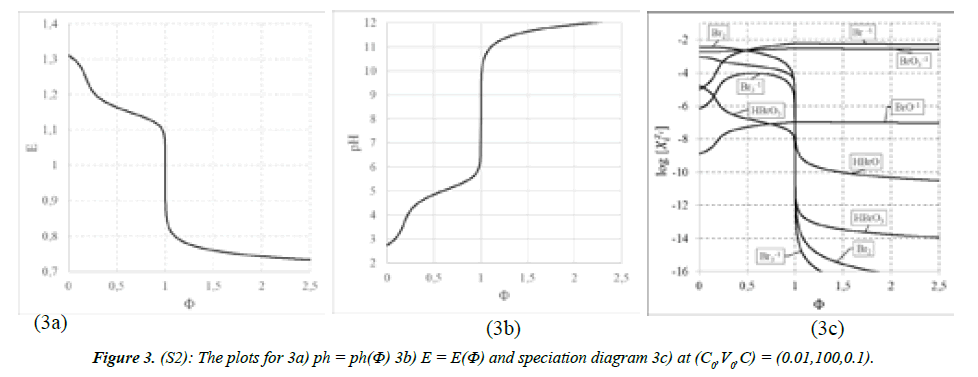
Systems S1 : NaOH ⇒ Br₂ and S2 : NaOH ⇒ HBrO: The curves are presented in (Figures 2A-C) for S1, and 3a,b,c for S2. The points (Φ,E,pH) from the vicinity of the related equivalence points on the titration curves: E = E(Φ) and pH = pH(Φ) are collected in Table 2. Moreover, from the result files we have the set of (Φ,pBrO₃,pBrO,pBr) values collected in Table 3, where:

Figure 2: (S1): The plots for (2a) ph = ph(Φ), (2b) E = E(Φ) and speciation diagram (2c) at (C₀,V₀,C) = (0.01,100,0.1).

pBrO₃ = –log[BrO₃^-1], pBrO = –log[BrO^-1], pBr = –log[Br^-1]

On this basis, we can compare two main competing reactions: (1a) and (1b) in the system S1, and:

3HBrO + 3OH^-1= BrO₃^-1 + 2Br^-1 + 3H₂O and (25)

HBrO + OH^-1 = BrO^-1 + H₂O (26)

in the system S2. Note that BrO-1 is the main competing product relative to BrO₃^-1, both in S1 and S2 (Figures 2C,3C), at a due excess of NaOH. On this basis, we find the relative efficiencies equal to 1041 (column 6) : 10^4.188 at Φ = 1.5 and 10^4.184 at Φ = 2.5 for reactions (1a), (1b); and 10^4.450 at Φ =1.5 and 2.5 for reactions (25) and (26). Note that (26) is the dissociation (not disproportionation) reaction. Stoichiometries of reactions (1a) and (1b) are the same for the competing pairs of reactions: 3:6 = 1:2 for reactions (1a), (1b), and 3:3 = 1:1 for reactions (25) and (26). Moreover, we find the ratio [BrO₃^-1]/[Br^-1] equal to 10⁴² = 10^0.699 = 5 = 5:1 for S1 at Φ = 2.5 (i.e. at the excess of NaOH), and close to 5 at the point where 1.5/2 = 75% of Br₂ is already consumed. The stoichiometry of products of reaction (25) is confirmed by the ratio [Br^-1]/[BrO₃^-1] = 10^0.301 = 2 = 2 : 1 (Table 3). This confirms the reaction 1a, and testifies against the reaction 1b (of the same stoichiometry!), commonly met (‘given to believe’) in literature and elsewhere, e.g. [38].

Figure 3: (S2): The plots for 3a) ph = ph(Φ) 3b) E = E(Φ) and speciation diagram 3c) at (C₀,V₀,C) = (0.01,100,0.1).

Symproportionation in dynamic bromine systems

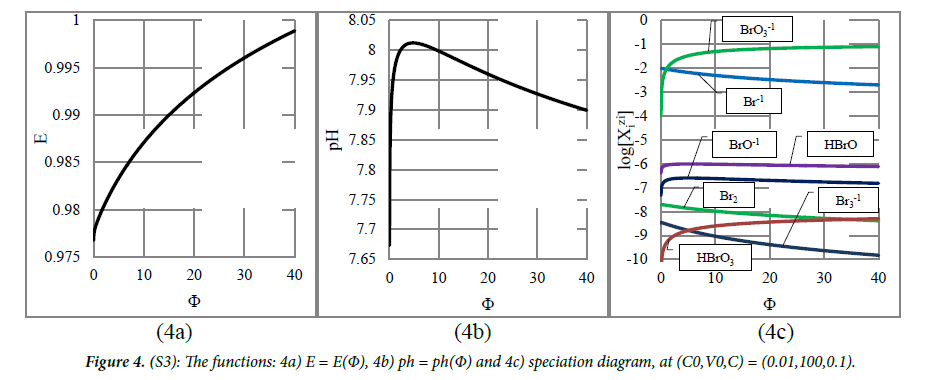
System 3 : kbro₃ ⇒ nabr: In this case, symproportionation practically does not occur (Figure 4C); concentration of HBrO, as the major product formed in the symproportionation reaction

BrO₃^-1 + 2Br^-1 + 3H⁺¹ = 3HBrO (27)

is ca. 10^-6 mol/L. The potential E increases monotonically (Figure 4A), whereas pH first increases, passes through maximum and then decreases (Figure 4B). The relevant pH and E changes are small. Binding the H⁺¹ ions in reaction (27) causes a weakly alkaline reaction (Figure 4B).

Figure 4: (S3): The functions: 4a) E = E(Φ), 4b) ph = ph(Φ) and 4c) speciation diagram, at (C₀,V₀,C) = (0.01,100,0.1).

Table 2 (S1,S2). The sets of (Φ, pH, E) values taken from the vicinity of the equivalence points, at (C₀,V₀,C) = (0.01,100,0.1).

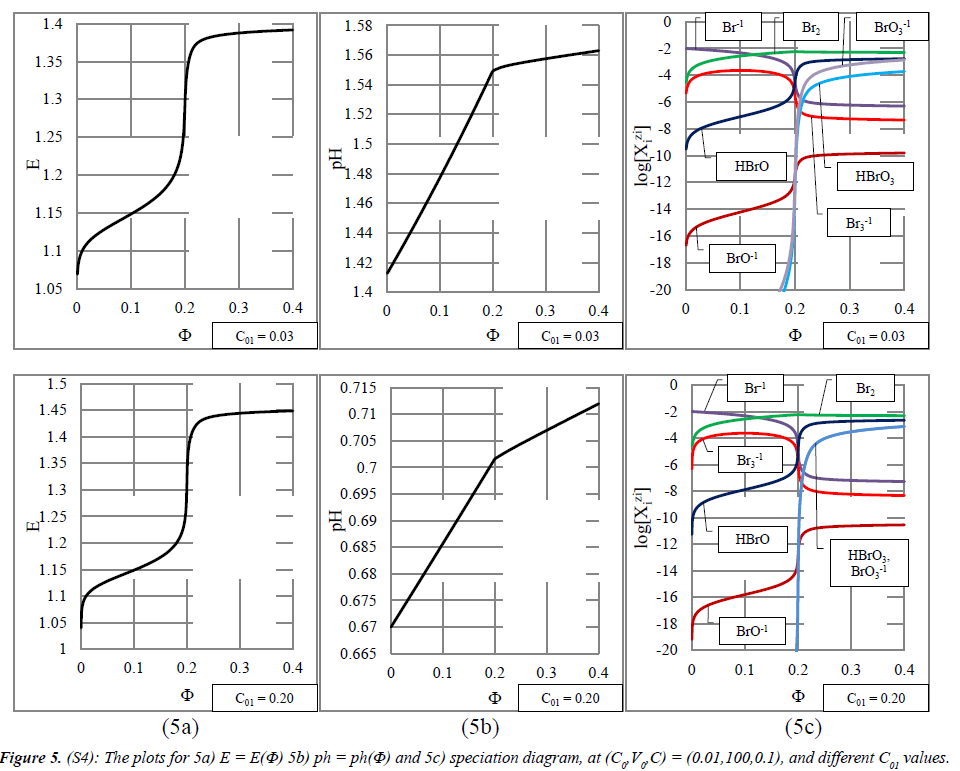
System S4 : KBrO₃ ⇒ NaBr + H₂SO₄: The stoichiometry 1 : 5, i.e., Φeq = 0.2, stated for C₀₁ values indicated at the curves plotted in Figure 5 (column 5a), results from reaction (2a). At Φ > 0.2, an increase of efficiency of the competing reaction (27) is noted. A growth of C01 value causes a small extension of the potential range in the jump region, on the side of higher E-values (Figure 5, column 5a). With an increase of the C₀₁ value, the graphs of pH vs. Φ resemble two almost straight line segments intersecting at Φ_eq = 0.2 (Figure 5, column 5b).

Figure 5: (S4): The plots for 5a) E = E(Φ) 5b) ph = ph(Φ) and 5c) speciation diagram, at (C₀,V₀,C) = (0.01,100,0.1), and different C₀₁ values.

However, the pH-ranges covered by the titration curves are gradually narrowed (Figure 5, column 5b).

System S5 : NaBrO ⇒ NaBr: The basic reaction in this system (Figure 6B) results from the relation

[HBrO₃]+[HBrO]+2[Br₂]+ 2[Br₃^-1] = [OH^-1] – [H⁺¹] > 0

Figure 6: (S5): The plots for 6a) E = E(Φ), 6b) ph = ph(Φ) and 6c) speciation diagram, at (C₀,V₀,C) = (0.01,100,0.1).

obtained for NaIO solution from combination (addition) of charge and concentration balances (Table 1):

α – P_2Br + β₀ + β = 0 and P_3Br = β0 + β. We get: – α = P_3Br – P_2Br = [HBrO] + 2[Br₂] + 2[Br₃^-1] > 0,

i.e., – α > 0 ⇒ α < 0 ⇒ [OH^-1] > [H⁺¹]. The disproportionation reactions

3HBrO = BrO₃^-1 + 2Br^-1 + 3H⁺¹ (28)

3BrO^-1 = BrO₃^-1 + 2Br^-1 (29)

occur in a small degree only in the initial step of the titration (Figure 6C), and then a basicity resulting from growth of NaBrO concentration in the system prevails over the growth in H+1 concentration resulting from reaction 28, i.e., dpH/dΦ > 0 (Figure 6B). Buffer capacity of NaBr solution is very low and even small changes in acidity cause substantial pH changes. Potential E passes through maximum, and then decreases (Figure 6A); this results from changes in [BrO₃^-1] and pH. The (small) growth in Br^-1 concentration, d[Br^-1]/dΦ > 0 (Figure 6B), resulting from reactions 28 and 29, overcomes the dilution effect in D+T, affected by T addition.

System S6: NaBrO ⇒ NaBr + H₂SO₄: Symproportionation occurs here mainly according to the scheme

HBrO + Br^-1 + H⁺¹ = Br₂ + H₂O (30)

(Figure 7C), stoichiometry 1:1. At Φ_eq = 1, there is a jump of the potential E (Figure 7A) and slightly marked fracture on the curve pH = pH(Φ) (Figure 7B). For Φ > 1, the excess of HBrO in the titrant disproportionates gradually according to schemes: 5HBrO = BrO₃^-1 + 2Br₂ + H⁺¹ + 2H₂O and 5HBrO = HBrO₃ + 2Br₂ + 2H₂O.

Figure 7: (S6): The plots for 7a) E = E(Φ), 7b) ph = ph(Φ) and 7c) speciation diagram, at (C₀,C₀₁,V₀,C) = (0.01,0.1,100,0.1).

System S7 : Br2 ⇒ NaBr: After the titrant addition, the concentration of Br₃^-1 increases in the reaction

Br₂ + Br^-1 = Br₃^-1 (31)

(Figure 8C); it affects the monotonic E-growth, (Figure 8A). Reaction (31) can be considered both as symproportionation (0, –1) → (–1/3), and as the complex formation. The Br₂ solution acts as a weak acid and then pH decreases (Figure 8B); this property of Br₂ results immediately from the charge balance: α = [H+1] – [OH^-1] = [BrO₃^-1]+[BrO^-1]+[Br₃^-1]+[Br^-1] > 0 for Br₂. The disproportionation Br₂ + H₂O = HBrO + Br^-1 + H+1 occurs to a small extent; the ratio [HBrO]/[Br₂] equals: 0.0113 at Φ=0.5; 0.0085 at Φ=1, 0.0068 at Φ=2. Other disproportionation products are formed with much lesser efficiency.

Figure 8: (S7): The functions 8a) E = E(Φ), 8b) ph = ph(Φ) and 8c) speciation diagram, at (C₀,V₀,C) = (0.01,100,0.1).

System S8: Br₂ ⇒ NaBr + H₂SO₄: Disproportionation of Br occurs here in very small degree (Figure 9C), smaller than in S7 (Figure 8C). The potential changes (Figure 9A) are very similar to those in Figure 8A. The pH changes are indicated in Figure 9B.

Figure 9: (S8): The functions 9a) E = E(Φ), 9b) ph = ph(Φ) and 9c) speciation diagram, at (C₀,C₀₁,V₀,C) = (0.01,0.1,100,0.1).

System S9: KBrO₃ ⇒ NaBr: In this case, symproportionation practically does not occur (Figure 10C); concentration of HBrO, as the major product formed in the symprortionation reaction

BrO₃^-1 + 2Br^-1 + 3H⁺¹ = 3HBrO (32)

is ca. 10^-6 mol/L. The potential E increases monotonically (Figure 10A), whereas pH first increases, passes through maximum and then decreases (Figure 10B). The relevant pH and E changes are small. Binding the H⁺¹ ions in reaction (32) causes a weakly alkaline reaction (Figure 10B).

Figure 10: (S9): The functions: 10a) E = E(Φ), 10b) ph = ph(Φ) and 10c) speciation diagram, at (C₀,V₀,C) = (0.01,100,0.1).

System S10 : KBrO₃ ⇒ NaBr + Br₂: The symproportionation effect (Figure 11C) is greater here than in the system 13 (Figure 11C), but is also small; concentration of HBrO, as the major product of the symproportionation (Eq. 32) is lower than 10^-3 mol/L (Figure 11C). The increase in [HBrO], can be accounted on symproportionation resulting from a weakly acidic solution, caused by the presence of Br₂, which disproportionates partially according to the scheme

Br₂ + H₂O = HBrO + Br^-1 + H⁺¹ (11)

compare with Figure 10C. The pH values (Figure 11B) cover acidic range, and E covers greater E values (Figure 11A) than those in Figure 10A.

Figure 11: (S10): The functions 11a) E = E(Φ), 11b) ph = ph(Φ) and 11c) speciation diagram, at (C₀,C₀₁,V₀,C) = (0.01,0.02,100,0.1).

System S11: KBrO₃ ⇒ NaBr + Br₂ + H₂SO₄:

The related graphs plotted at different concentrations C0₂ of H₂SO₄ are shown in Figure 12. From a comparison of the graphs in the related columns of Figures 7 and 12 it follows that the presence of Br₂ in D affects the related graphs. However, the position of inflection points in Figures 7A and 12A, and breaking points in Figures 7B and 12B are the same, in principle.

Figure 12: (S11): The functions 12a) E = E(Φ), 12b) ph = ph(Φ) and 12c) speciation diagrams, at (C₀,C₀₁,V₀,C) = (0.01,0.02,100,0.1), and different C₀₂ values.

Final comments

The paper presents dynamic redox systems, with bromine species on different ONs involved. The systems were tested in simulation procedures, realized according to GATES/GEB principles. The results of calculations made with use of iterative computer programs, were presented graphically. On the basis of speciation curves, the reactions occurred in the systems can be formulated, together with their relative efficiencies. Among others, the effects resulting from presence of H₂SO₄ in the titrand, are considered and illustrated graphically

The Generalized approach to electrolytic systems (GATES) with the Generalized electron balance (GEB) involved and termed therefore as GATES/GEB, is adaptable for resolution of thermodynamic (equilibrium and metastable) redox systems of any degree of complexity; none simplifying assumptions are needed. Application of GATES provides the reference levels for real analytical systems. The GATES makes possible to exhibit some important details, of qualitative and quantitative nature, invisible in real experiment, e.g. speciation.

Contrary to appearances, the available physicochemical knowledge on the thermodynamic properties of basic species formed by halogens: chlorine, bromine and iodine in aqueous media, raises fundamental doubts, both of qualitative, and quantitative nature.

The knowledge of equilibrium constants, collected in the past/ distant times, for decades, is not substantially supplemented and verified in contemporary times. Frankly, the physicochemical analysis of electrolytic systems is not currently one of the top issues raised in scientific research. The quantitative data published in literature are closely related to the quality of mathematical models applied to their determination in electrochemical research, with the main emphasis put on potentiometry. The stoichiometry concept, based on the chemical reaction notation principle, and especially its use and abuse, have been criticized repeatedly by the author, especially in the works [8,19,20,32-34] issued in recent years. Stoichiometry cannot be perceived as a true mathematics consequently inherent within chemistry. Additionally, significant uncertainties arise in the context of instability of the relevant compounds in aqueous solutions, raised e.g., under the links [39,40], and in the literature cited therein. In particular, the instability of some compounds after their introduction into aqueous media is explained rightly by their disproportionation. However, the disproportionation scheme suggested this way (i.e., a priori) is inconsistent with the results of calculations carried out on the basis of the physical laws of elements conservation and equilibrium constants values.

The f₁₂ , and any linear combination of f₁₂ with f₀,f₃,…,f_K , have full properties of Generalized Electron Balance (GEB), completing the set of K balances, f₀,f₁₂,f₃,…,f_K, needed for resolution of a redox system, of any degree of complexity. The K–1 balances f₀,f₃,…,f_K are needed for resolution of a redox system, of any degree of complexity. The linear independency/ dependency of f₀,f₁₂,f₃,…,fK is then the general criterion distinguishing between redox and non-redox systems. The supreme role of this independency/dependency criterion, put also in context with calculation of ONs, is of great importance, in context with the contractual nature of the ON concept [41,42], known from the literature issued hitherto. These regularities are the clear confirmation of the Emmy Noether’s general theorem [43-50] applied to conservation laws of a physical/ electrolytic system, expressed in terms of algebraic equations, where GEB is perceived as the Law of Nature, as the hidden connection of physicochemical laws, and as the breakthrough in thermodynamic theory of electrolytic redox systems.

References

1. http://en.wikipedia.org/wiki/Disproportionation
2. http://goldbook.iupac.org/html/S/S06215.html
3. Micha?owski  T,  Lesiak  A.  Acid-base  titration   curves in disproportionating redox systems. J Chem Educ. 1994:71(8): 632-6.
4. Afanas'ev I.B. Superoxide Ion Chemistry and Biological Implications. CRC Press, Inc, Boca Raton, Florida.1989:1.
5. https://fr.wikipedia.org/wiki/Dismutation
6. http://goldbook.iupac.org/html/C/C01217.html
7. https://en.wikipedia.org/wiki/Comproportionation
8. http://www.chemeurope.com/en/encyclopedia/ Synproportionation.html
9. Micha?owski T. Application of GATES and MATLAB for Resolutionof Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems. Applications of MATLAB in Science and Engineering (ed. by T. Micha?owski), InTech - Open Access publisher in the fields of Science, Technology and Medicine. 2011;1:1-34.
10. Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. Principles of Titrimetric Analyses According to Generalized Approach to Electrolytic Systems (GATES), in: Advances in Titration Techniques, Vu Dang Hoang (Ed.) In Tech Chap. 2017;5:133-71.
11. Micha?owski T, Toporek M, Micha?owska-Kaczmarczyk AM et al. New Trends in Studies on Electrolytic Redox Systems. Electrochimica Acta.2013;109:519-31.
12. Micha?owski T, Micha?owska-Kaczmarczyk AM, Toporek M. Formulation of general criterion distinguishing between non-redox and redox systems. Electrochimica Acta.2013;112: 199-11.
13. Micha?owska-Kaczmarczyk AM, Micha?owski T. Comparative balancing of non-redox and redox electrolytic systems and its consequences. Am J Analyt Chem.2013;4(10): 46-53.
14. http://file.scirp.org/Html/38569.html
15. Micha?owska-Kaczmarczyk AM, Rymanowski M, Asuero AG, et al. Formulation of Titration Curves for Some Redox Systems. Am J Analyt Chem.2014;5:861-78.
16. Toporek M, Micha?owska-Kaczmarczyk AM, Micha?owski T. Disproportionation Reactions of HIO and NaIO in Static and Dynamic Systems. Am J Analyt Chem.2014;5:1046-56.
17. Micha?owska-Kaczmarczyk AM, Micha?owski T. Generalized Electron Balance for Dynamic Redox Systems in Mixed-Solvent Media. Journal of Analytical Sciences.Methods and Instrumentation. 2014;4(4):102-9.
18. Micha?owska-Kaczmarczyk AM, Micha?owski T. Compact formulation of redox  systems  according  to  GATES/ GEB principles. Anal Sci. Methods and Instrumentation.2014;4(2):39-45.
19. Micha?owska-Kaczmarczyk AM, Toporek M, Micha?owski T. Speciation Diagrams in Dynamic Iodide + Dichromate System. Electrochimica Acta. 2015;155:217-27.
20. Toporek M, Micha?owska-Kaczmarczyk AM, Micha?owski T.Symproportionation    versus     Disproportionation in Bromine Redox Systems. Electrochimica Acta. 2015;171:176-87.
21. Micha?owska-Kaczmarczyk AM, Asuero AG, Toporek, et al. ?Why not stoichiometry? versus ?Stoichiometry-why not?? Part II. GATES in context with redox systems. Crit Rev Anal Chem. 2015;45(3): 240-68.
22. https://www.researchgate.net/publication/274643245_ Why_Not_Stoichiometry_Versus_Stoichiometry-Why_ Not_Part_II_GATES_in_Context_with_Redox_Systems
23. Micha?owska-Kaczmarczyk AM, Micha?owski T, Toporek M, et al. ?Why not stoichiometry? versus ?Stoichiometry - why not?? Part III, Extension of GATES/GEB on Complex Dynamic Redox Systems. Critical Reviews in Analytical Chemistry. 2015;45(4):348-66.
24. https://docksci.com/geb-on-complex-dynamic-redox- systems_5a56b200d64ab2f2215ccf7a.html
25. http://www.researchgate.net/publication/274401037_ Why_Not_Stoichiometry_Versus_Stoichiometry_-_Why_ Not_Part_III_Extension_of_GatesGeb_on_Complex_ Dynamic_Redox_Systems
26. Micha?owski T, Pilarski B, Asuero AG, et al. Modelling  of Acid-Base Properties in Binary-Solvent Systems. In "Handbook of Solvents", Properties, Wypych G. (Editor), chemtec Publishing, Toronto. 2014;1(4):623-48.
27. Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. Generalized Electron Balance (GEB) as the Law of Nature in Electrolytic Redox Systems, in: Redox: Principles and Advanced Applications, Ali Khalid, M.A. (Ed.) InTech Chap. 2017;2:9-55.
28. Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. A Distinguishing Feature of the Balance 2?f(O) ? f(H) in Electrolytic Systems. The Reference to Titrimetric Methods of Analysis, in: Advances in Titration Techniques. Vu Dang Hoang (Ed.) Intech. 2017;6:173-207.
29. Micha?owska-Kaczmarczyk AM, Spórna-kucaba, Micha?owski T. Solubility products and solubility concepts, in: Descriptive Inorganic Chemistry. Researches of Metal Compounds. Akitsu T. (Ed.) InTech Chap 5:93-134.
30. https://cdn.intechopen.com/pdfs-wm/55440.pdf
31. Micha?owski T, Baterowicz A, Madej A, et al. An extended Gran method and its applicability for simultaneous determination of Fe(II) and Fe(III). Analytica Chimica Acta. 2001;442(2): 287-93.
32. http://www.sciencedirect.com/science/article/pii/ S0003267001011722
33. Micha?owski T, Toporek M, Rymanowski M. Overview on the Gran and other linearization methods applied in titrimetric analyses. Talanta. 2005;65(5):1241-1253.
34. T Micha?owski, K Kupiec, M Rymanowski. Numerical analysis of the Gran methods. A comparative study. Analytica Chimica Acta. 2008;606(2):172-83.
35. http://suw.biblos.pk.edu.pl/resourceDetails&rId=4745%7 D%7D%3C/opinion&rId=24153
36. Ponikvar M, Micha?owski T, Kupiec K et al. Experimental verification of the modified Gran methods applicable to redox systems. Analytica Chimica Acta.2008;628(2):181-89.
37. Micha?owska-Kaczmarczyk AM, Micha?owski T. Linear Dependence of Balances for Non-Redox Electrolytic Systems. Am J Analyt Chem. 2014;5:1285-89.
38. Marx D, Tuckerman ME, Hutter J. The nature of the hydrated excess proton in water. Nature. 1999;397:601-4.
39. Micha?owska-Kaczmarczyk AM, Spórna-Kucab A, Micha?owski T. The balance 2?f(O) ? f(H) as a keystone in formulation of electrolytic systems. Research and Reviews in Computational Chemistry. 2018;1(1):1-9.
40. http://rrcchemistry.com/index.php/rrcc/article/view/1/1
41. http://rrcchemistry.com/index.php/rrcc/issue/current
42. Micha?owski T. The Generalized Approach to Electrolytic Systems: I. Physicochemical and Analytical Implications. Critical Reviews in Analytical Chemistry. 2010;40:2-16.
43. Micha?owski T, Pietrzyk A, Ponikvar-Svet, et al. The Generalized Approach to Electrolytic Systems: II. The Generalized Equivalent Mass (GEM) Concept. Crit Rev Anal Chem. 2010;40:17-29.
44. Micha?owska-Kaczmarczyk AM, Asuero AG, Micha?owski T. ?Why not stoichiometry? versus ?Stoichiometry ? why not?? Part I. General context. Crit Rev Anal Chem. 45: 166-88.
45. Cortassa S, Aon MA, Iglesias AA, et al. An Introduction to Metabolic and Cellular Engineering. World Scientific Publishing Co. Pte Ltd. New Jersey. 2002;47.
46. Qiu Y, Gao Y, Wei P, et al. Organic light-emitting diodes with improved hole-electron balance by using copper phthalocyanine/aromatic diamine multiple quantum wells. Appl Phys Lett. 2002;80: 26-28.
47. Callwood K. How to Use an Electronic Balance.
48. Michalowski T. Calculation of pH and potential E for bromine aqueous solutions. J Chem Educ.1994;71(7):560-62.
49. h t t p s : / / w w w . w e b q c . o r g / b a l a n c e . php?reaction=Br2+%2B+%28OH%29%7B- % 7 D + % 3 D + H 2 O + % 2 B + B r % 7 B - %7D+%2B+%28BrO%29%7B-%7D
50. https://en.wikipedia.org/wiki/Halogen