Case Report - Journal of Agricultural Science and Botany (2017) Volume 1, Issue 1
Water resources management optimization and development of sustainable agriculture, case study: Pakdasht plain
Shiva Ourang*
School of Civil Engineering, Company Falate Pars Co. consultant Engineer, College of Engineering, University of Tehran, Iran
- *Corresponding Author:
- Ourang S
School of Civil Engineering
Company Falate Pars Co. consultant Engineer
College of Engineering
University of Tehran, Iran
E-mail: shiva.ourang@gmail.com
Accepted on December 07, 2017
Citation: Ourang S. Water resources management optimization and development of sustainable agriculture, case study: Pakdasht plain.. J Agric Sci Bot 2017;1(1):18-22.
DOI: 10.35841/2591-7897.1.1.25-29
Visit for more related articles at Journal of Agricultural Science and BotanyAbstract
Currently, water is very valuable, so should be used optimally. Planning for optimal use of water and soil resources will protect these resources and bring about increased production, growth in farm income, and enhancement of rural economic prosperity. This study was performed with the aim of improving management of water resources on Pakdasht Plain lands using a combination of typical and linear goal optimization techniques that in this study are used to examine optimal allocation of water and prioritization of cultivation patterns with respect to water consumption. In this study, the effects of limits on irrigation on the products of system cultivation patterns have also been evaluated, with results that indicate that Option 16, with a 0.33 profit on consumed water, produces the greatest financial efficiency, while Option 22 shows the lowest financial efficiency of 0.22. The findings suggest that the planning axis (water profit and productivity or sustainability in use of groundwater resources) plays a key role in the process of managing and allocating system water resources.
Keywords
Conjunctive harvesting, Water productivity, Optimization, Pakdasht irrigation system, Goal programming.
Introduction
Because Iran is located in a warm and dry region, most plains of Iran require proper management of water resources and optimization of water consumption to maximize exploitation of limited water resources [1,2]. A sustainable water management policy for agricultural irrigation is to promote water use in such a way that society’s needs are met to the greatest extent possible, both now and in the future. Linear Programming (LP) and principal components analysis have long been used to select descriptive variables for relating runoff to climate and watershed descriptors [3,4]. Statistical prediction methods, on the other hand, rely on past historical data for prediction [5-9]. LP approaches have always been used to obtain optimal strategies, such as water-allocation patterns, crop-planting plans, and canal-expansion schemes, with the objective of maximizing net benefit [10]. One of the main solutions in the agriculture sector, the largest consumer of water resources, is conjunctive use of surface and ground water resources. Launching a suitable and optimal cultivation pattern undoubtedly can have a significant effect on reducing water consumption and elevating profits in an agriculture system [11-15]. The main aim of this study is development and application of a model for managing surface and ground water resources and achieving an optimal cultivation pattern.
Case Study
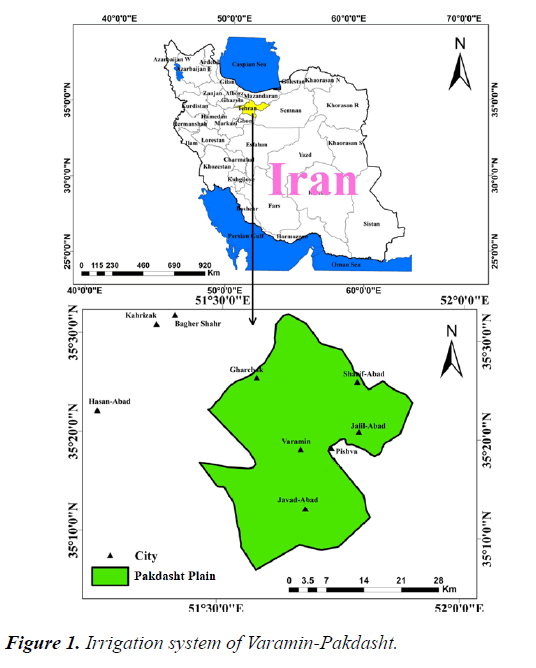
The Pakdasht Plain is located in the northern part of Iran in the southern ranges of Alborz, 40 km southeast of Tehran, between 33° and 51° up to 40° and 41° of eastern longitude, and 5° and 35° up to 30° and 35° of the northern latitude [16]. The area under cultivation by the irrigation system is approximately 50000 hectares, with a soil suitable for agriculture resulting from the deposition of Jajrood River sediments, as shown in Figure 1 [17].
The cultivation area of the Plain is approximately 130,000 hectares, the range of the modern irrigation and drainage plan is approximately 50,000 hectares, the area of first-degree land in agriculture is 80,000 hectares, the area of land under modern irrigation is currently between 60 and 65,000 hectares (60,000 hectares under irrigation coverage), with approximately 32 hectares (53%) related to Varamin and 28 hectares (47%) related to Pakdasht. In this study, given the current water supply for at most 75000 hectares, planning and determination of cultivation patterns were performed [18].
This method assumes that the climatic needs of the product are met, and water, nutrient, salinity, pests, and diseases do not affect the growth and potential function of the product (Ym). The cultivation pattern of the region should be used to calculate the maximum and actual performances. The common pattern in the Pakdasht Plain includes wheat, barly, corn, alfalfa, cotton, and cucurbits, irrigated by Faro and band irrigation methods.
Methods and Materials
The general structure of a fractional multi-objective goal programming model can be formulated as shown in Equation 1.
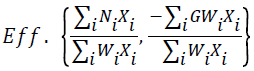 (1)
(1)
where i is number of products (i=1,2,…), Ni is the net profit of the ith product except for water cost, Xi is the area under cultivation for the ith product in the region (in hectares), Wi is the total water consumed for the ith product in the cultivation season (102 m3/ha), GWi is the groundwater used in the region for the ith product (102 m3/ha), 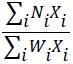 is the total profit for the total water consumed (productivity), and
is the total profit for the total water consumed (productivity), and 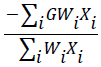 is the ratio of total groundwater to the total water consumed.
is the ratio of total groundwater to the total water consumed.
The first model involves linear programming (LP1) for profit maximization. This model has been developed considering different values of reduction or increase of withdrawal from groundwater [19]. For all of the above-mentioned options, the LP1 model was written and the values of areas of cultivation and consumed water were compared.
The second model involves linear programming (LP2) for minimizing use of groundwater. According to the authorities of irrigation affairs of the region, if the extent of withdrawal is reduced by 25% in comparison with the current value, the water balance of the plain will reach zero [20]. In the third model, linear goal programming (LGP) was used to simultaneously maximize profit and minimize groundwater use. The aim was to determine LP1 and LP2 values, with each value set as a goal for achieving these conditions as closely as possible, while considering the importance of each.
Results and Discussion
In this study, 22 options were studied. The first was to use the typical cultivation patterns of the region with respect to wheat, barley, alfalfa, cotton, and cucurbits (tomato, eggplant, and pumpkin). The current total area under cultivation in the region is 52,455 hectares, and the maximum area under cultivation is currently allocated to barley, then to wheat, with respective values of 13,500 and 13,075 hectares.
For the second to tenth options, different amoiunts of groundwater reduction were applied, and the profit and areas under cultivation were compared with one another. These options were chosen to preserve or improve the situation with respect to groundwater aquifers. In these options, reductions ranging from 60% to 0% were considered. The total groundwater volume for this purpose varied between 179.44 and 448.61 million m3 per year for the second to tenth options.
In the eleventh to sixteenth options, increase of withdrawal from groundwater was considered to examine the resulting trend of changes with respect to profit and areas under cultivation. This increased withdrawal was incremented by up to 25%, i.e., up to 560.76 million m3/year. For these options, increased groundwater withdrawal causes excessive pressure on groundwater aquifers (Table 1).
| Total cultivated area under deficit conditions | Total cultivated area under ideal condition | Dehydration rate | μ | Options |
|---|---|---|---|---|
| - | - | - | - | 1 |
| - | - | 0 | 0.4 | 2 |
| - | - | 0 | 0.5 | 3 |
| - | - | 0 | 0.6 | 4 |
| - | - | 0 | 0.7 | 5 |
| 40904 | 40699 | 0 | 0.8 | 6 |
| 40904 | 40699 | 0 | 0.85 | 7 |
| 40904 | 40699 | 0 | 0.9 | 8 |
| 40904 | 40699 | 0 | 0.95 | 9 |
| 40904 | 40699 | 0 | 1 | 10 |
| 40904 | 40699 | 0 | 1.05 | 11 |
| 40904 | 40699 | 0 | 1.1 | 12 |
| 40904 | 40699 | 0 | 1.15 | 13 |
| 40904 | 40699 | 0 | 1.2 | 14 |
| 40904 | 40699 | 0 | 1.25 | 15 |
| 41463 | 47578 | 0 | 1 | 16 |
| 41700 | 50437 | 10 | 1 | 17 |
| 41700 | 52927 | 15 | 1 | 18 |
| 41700 | 56655 | 20 | 1 | 19 |
| 41700 | 59394 | 25 | 1 | 20 |
| 41700 | 61163 | 30 | 1 | 21 |
| 41700 | 74165 | 40 | 1 | 22 |
Table 1. Introduction of the studied options and their areas under cultivation.
The 16th to 22nd options have been allocated different reduced irrigation levels. Implementing reduced irrigation by up to 40% and calculating the performance value resulted in the area under cultivation growing by up to 74165 hectares, a 41% increase in the area under cultivation.
To obtain values for the optimal cultivation areas, each of the above options was written and solved using three models.
Linear programming LP1
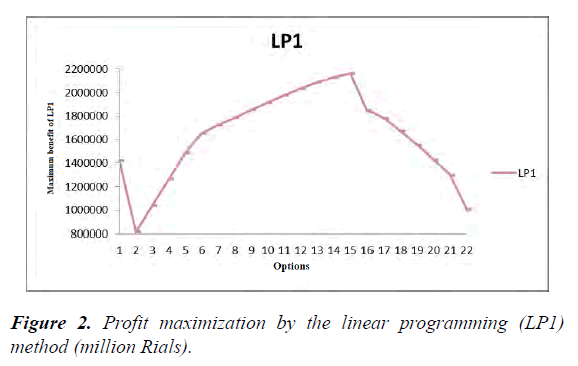
For all options, the entire volume of available surface water in the plain (141.92 billion m3/year) was used. The maximum profit was associated with Option 15, representing 25% more groundwater withdrawal, about 560.76 million m3/year, in relation to current conditions. In this option, the profit is 1.52 times as large as that for the current state (2162 billion Rials). Implementation of this option is only possible if the groundwater aquifers could be fed by resources other than the internal resources of the plain, otherwise we would observe a dramatic decrease in the water table level of Pakdasht Plain.
Minimum profit occurs for Option 2, where groundwater withdrawal decreases by 60% (179.4 million m3/year) in comparison to the current state. For this case, the profit reaches 0.57 of the current value (816.4 billion Rials). Implementation of this option, representing a descending trend in water table level of the region in the upcoming years, would be likely to ultimately result in devastation of the plain. For other options with elevated groundwater withdrawal (Options 2 to 15), the profit grows. This increase grows faster in Options 2 to 6 than in options 7-15. In other options (16 to 22), if low irrigation is implemented, although the area under cultivation grows, the profit diminishes significantly. The results obtained from the linear model of profit maximization and areas under cultivation are shown in Table 2 and Figure 2.
| Total | Cotton | Cucurbits | Alfalfa | Forage corn | Barley | Wheat | Options |
|---|---|---|---|---|---|---|---|
| 28907 | 0 | 6935 | 2022 | 1750 | 9100 | 9100 | 2 |
| 33835 | 0 | 10197 | 3688 | 1750 | 9100 | 9100 | 3 |
| 38654 | 0 | 13458 | 5246 | 1750 | 9100 | 9100 | 4 |
| 42669 | 0 | 16719 | 6000 | 1750 | 9100 | 9100 | 5 |
| 45520 | 2570 | 17000 | 6000 | 1750 | 9100 | 9100 | 6 |
| 43945 | 3000 | 17000 | 2580 | 3165 | 9100 | 9100 | 7 |
| 48399 | 3000 | 17000 | 4996 | 5203 | 9100 | 9100 | 8 |
| 51443 | 3000 | 17000 | 6000 | 7243 | 9100 | 9100 | 9 |
| 53482 | 3000 | 17000 | 6000 | 9282 | 9100 | 9100 | 10 |
| 55200 | 3000 | 17000 | 6000 | 11000 | 9100 | 9100 | 11 |
| 55200 | 3000 | 17000 | 6000 | 11000 | 9100 | 9100 | 12 |
| 55200 | 3000 | 17000 | 6000 | 11000 | 9100 | 9100 | 13 |
| 56725 | 3000 | 17000 | 6000 | 11000 | 9100 | 10625 | 14 |
| 58623 | 3000 | 17000 | 6000 | 11000 | 9100 | 12523 | 15 |
| 55200 | 3000 | 17000 | 6000 | 11000 | 9100 | 9100 | 16 |
| 55200 | 3000 | 17000 | 6000 | 11000 | 9100 | 9100 | 17 |
| 57543 | 3000 | 17000 | 6000 | 11000 | 9100 | 11443 | 18 |
| 61798 | 3000 | 17000 | 6000 | 11000 | 9100 | 15698 | 19 |
| 66620 | 3000 | 17000 | 6000 | 11000 | 9100 | 20520 | 20 |
| 72130 | 3000 | 17000 | 6000 | 11000 | 9100 | 26030 | 21 |
| 88408 | 3000 | 17000 | 6000 | 11000 | 22408 | 29000 | 22 |
Table 2. The areas under cultivation of linear programming for profit maximization across different options (hectares).
As shown in Table 2, with decreased groundwater withdrawal and without applying reduced irrigation, the area under cultivation in the plain decreased, and in the minimum state it reached 28,635 hectares in Option 2. As expected, in this state the areas under cultivation approach the lower limit set for them, and the area under cultivation of the crops decreased significantly with huge water consumption. By applying reduced irrigation and associated water stress by up to 40%, the total area under cultivation reached 88,408 hectares (Option 22). If this option and other options are investigated, the deficit of irrigation water for the mentioned plain becomes more evident. Implementation of option (22), considering its low water productivity (0.17), would only be recommended for reasons other than profit, perhaps for cultivating a large area of the plain to improve employment conditions.
The linear programming LP2
This model is for minimization of groundwater withdrawal. According to the water authorities of Pakdasht Plain, if groundwater withdrawal decreases by about 25% in comparison with the previous year, i.e., it reaches 336.46 million m3 per year, the extents of plain withdrawal and feeding become equal and the aquifer level remains constant. Thus, across all LP2 options, the groundwater level remains constant at 336.46 million m3.
Goal programming
Based on the goal values obtained by solving the above linear models (LP1, LP2), using goal programming the resulting composition and area under cultivation of the region’s crops are given in Table 3.
| Total | Cotton | Cucurbits | Alfalfa | Forage Corn | Barley | Wheat | Option | Products |
|---|---|---|---|---|---|---|---|---|
| 52455 | 230 | 12700 | 4450 | 8500 | 13500 | 13075 | current | 1 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=0.8 | 6 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=0.85 | 7 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=0.9 | 8 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=0.95 | 9 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=1 | 10 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=1.05 | 11 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=1.1 | 12 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=1.15 | 13 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=1.2 | 14 |
| 40699 | 1999 | 17000 | 1750 | 1750 | 9100 | 9100 | μ=1.25 | 15 |
| 47578 | 3000 | 17000 | 1750 | 7628 | 9100 | 9100 | RI=5 | 16 |
| 50437 | 3000 | 17000 | 1750 | 10487 | 9100 | 9100 | RI=10 | 17 |
| 52927 | 3000 | 17000 | 3727 | 11000 | 9100 | 9100 | RI=15 | 18 |
| 56655 | 3000 | 17000 | 4087 | 11000 | 9100 | 12468 | RI=20 | 19 |
| 59394 | 3000 | 17000 | 6000 | 11000 | 9100 | 13294 | RI=25 | 20 |
| 61163 | 3000 | 17000 | 6000 | 11000 | 9100 | 15063 | RI=30 | 21 |
| 74165 | 3000 | 17000 | 6000 | 11000 | 9100 | 28065 | RI=40 | 22 |
Table 3. Composition and area under cultivation of region’s crops resulting from the linear programming method (hectares).
These values are intermediate limits for obtaining maximum profit and minimum water consumption. Indeed, attempts have been made to achieve maximum profit by consuming only a minimum level of groundwater. Options 2 to 5 cannot be solved by goal programming because their goals are in contradiction. The goal value for options 6 to 15 is a constant, so the profit and areas under cultivation are the same for all. In these options, groundwater withdrawal has been varied over ranges between 0.8 of the current withdrawal in Option 2 and 1.25 times larger than as the withdrawal in Option 15. This suggests that the volume of groundwater withdrawn varies from 448.89 million m3 in Option 6 to 560.76 million m3 in Option 15.
Based on Tables 1-3, it can be deduced that with lesser irrigation, the performance of the crops has diminished, and the descending slope of these changes is different for different products. For example, at a water stress of 5%, the minimum crop reduction was associated with cotton where, by applying 5% lower irrigation, we observed only a 4.2% reduction. This means that cotton performance under complete irrigation conditions decreases from 4096.56 to 3922.48 kg/hectares under 5% stress conditions. At this stress, the maximum performance reduction was associated with barley, a 5.8% reduction from 4459.53 from 4731.62 kg/hectares. Indeed, the most sensitive crop in terms of water stress level of 5% is barley, while the most resistant is cotton. For other products, we observe 5.2% reductions.
Conclusion
The extent of surface water allocated across all options is 141.92 million m3/year, and this corresponds to only a small part of the plain’s irrigation demands. The extent of current groundwater withdrawal is 448.61 million m3/year, and considering the droughts in recent years, this has caused a dramatic decrease in the water table level of this plain.
Comparison of Options 2 to 15, representing complete irrigation, indicates that with increased groundwater withdrawal, the area under cultivation has grown, and the net profit in turn also increased. The maximum profit of 2162.47 billion Rials can be obtained in Option 15 with a 25% increase in groundwater withdrawal, with the area under cultivation increased by 58,623 hectares.
In this study, the effect of application of reduced irrigation on crops in the system’s cultivation pattern was examined, with results indicating that, for implementing Options 16 and 17, corresponding to 5 and 10% reduced irrigation, the extent of groundwater allocation decreases from 448.61 to 338.108 and 317.634 million m3/year, respectively, representing 26.63 and 29.2% decrease in withdrawal.
As mentioned previously, for a 25% decrease in groundwater withdrawal, the plain’s balance has reached zero, and the level of groundwater aquifers stays at a constant value.
The results also indicate that Option 16 has represents the maximum financial efficiency, with a profit-to-water consumed ratio of 0.33, while Option 22 represents minimum financial efficiency with a value of 0.2225. Option 22 with a groundwater-to-total water consumed ratio of 0.5518, and Options 6-16 exert the minimum and maximum amounts, respectively, of pressure to groundwater resources. This suggests that, although increased groundwater withdrawal causes incremental profit, because it also leads to elevated consumption of water resources, it will bring about diminished water productivity.
These research findings suggest that the planning axis (profit and water productivity or stability in use of groundwater resources) plays a key role in the process of management and allocation of water resources of the system, and under abnormal conditions and crises resulting from drought or climate change, a different approach would be demanded.
References
- Nahvi A, Daghighi A, Nazif S. The Environmental Impact Assessment of Drainage Systems: A Case Study of the Karun River Sugarcane Development Project. Arch Agron Soil Sci. 2017;185-95.
- Akram M, Azari A, Nahvi A, et al. Subsurface drainage in Khuzestan, Iran: environmentally revisited criteria. Irrigation and Drainage. 2013;62(3):306-14.
- Llamas MR, Custodio E. Intensive use of groundwater: a new situation which demands proactive action. Intensive use of groundwater: Challenges and opportunities. 2003:13-31.
- Lu HW, Huang GH, Zeng GM, et al. An inexact two-stage fuzzy-stochastic programming model for water resources management. Water Resour Manag. 2008:22(8);991-1016.
- Castelletti A, Pianosi F, Soncini-Sessa R. Integration, participation and optimal control in water resources planning and management. Appl Math Comput. 2008;206(1):21-33.
- Lu H, Huang G, He L. An inexact rough-interval fuzzy linear programming method for generating conjunctive water-allocation strategies to agricultural irrigation systems. Appl Math Model. 2011;35(9):4330-40.
- Daghighi A. Harmful Algae Bloom Prediction Model for Western Lake Erie Using Stepwise Multiple Regression and Genetic Programming 2017.
- Lu HW, Huang GH, Lin YP, et al. A two-step infinite α-cuts fuzzy linear programming method in determination of optimal allocation strategies in agricultural irrigation systems. Water Resour Manag. 2009;23(11):2249-69.
- He L, Huang GH, Zeng GM, et al. Wavelet-based multiresolution analysis for data cleaning and its application to water quality management systems. Expert Syst Appl. 2008;35(3):1301-10.
- Anwar AA, Clarke D. Irrigation scheduling using mixed-integer linear programming. J Irrig Drain Eng. 2001;127(2):63-9.
- Lawston PM, Santanello Jr, JA Franz, et al. Assessment of irrigation physics in a land surface modeling framework using non-traditional and human-practice datasets. Hydrol Earth Syst Sci. 2017;21(6):2953-66.
- Leng G, Leung LR, Huang M. Significant impacts of irrigation water sources and methods on modeling irrigation effects in the ACME Land Model. J Adv Model Earth Sy. 2017;9(3):1665-83.
- Daghighi A, Nahvi A, Kim U. Optimal Cultivation Pattern to Increase Revenue and Reduce Water Use: Application of Linear Programming to Arjan Plain in Fars Province. Agriculture. 2017;7(9):73.
- Battude M, Al Bitar A, Brut A, et al. Modeling water needs and total irrigation depths of maize crop in the south west of France using high spatial and temporal resolution satellite imagery. Agric Water Manag. 2017;189:123-36.
- Karandish F, Simunek J. Two-dimensional modeling of nitrogen and water dynamics for various N-managed water-saving irrigation strategies using HYDRUS. Agric Water Manag. 2017;193:174-90.
- Barthold VV. An historical geography of Iran. Princeton University Press. 2014.
- Nikoo MR, Kerachian R, Malakpour-Estalaki S, et al. A probabilistic water quality index for river water quality assessment: a case study. Environ Monit Assess. 2011;181(1-4):465-78.
- Karamidehkordi E. A country report: challenges facing Iranian Agriculture and Natural Resource Management in the twenty-first century. Hum Ecol. 2010;38(2):295-303.
- Bussieck MR, Meeraus A. General algebraic modeling system (GAMS). Applied Optimization. 2004;88:137-58.
- Karamouz M, Kerachian R, Zahraie B. Monthly water resources and irrigation planning: case study of conjunctive use of surface and groundwater resources. J Irrig Drain Eng. 2004;130(5):391-402.