- Biomedical Research (2012) Volume 23, Issue 3

Stress distribution in the mandibular central incisor and periodontal ligament while opening the bite: A finite element analysis

Weijun Yana, Xiaohui Jiaob^*, Ping Shaoa,c, Wei Caid

¹Department of Orthodontics, The First Affiliated Hospital of Harbin Medical University, Harbin 150001, Hei Long Jiang Province, China.

²Department of Oral and Maxillofacial Surgery, The First Affiliated Hospital of Harbin Medical University, Harbin 150001, Hei Long Jiang Province, China.

³School of Material Science and Engineering, Harbin Institute of Technology, Harbin 150001, Hei Long Jiang Province, China.

⁴Department of Materials Science & Engineering, Harbin Institute of Technology, Harbin 150001, Hei Long Jiang Province, China.

Corresponding Author:

Xiaohui Jiao
Department of Oral and Maxillofacial Surger
The First Affiliated Hospital of Harbin Medical University
No. 23 Youzheng Street Nangang District Harbin, P.R.China.

Accepted date: March 02 2012

Abstract

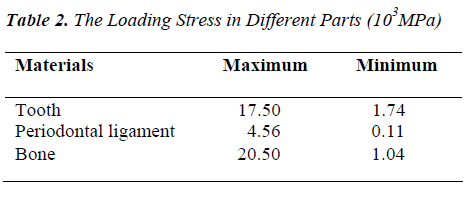
A finite element model is used to explore the stress-strain responses of the mandibular central incisor and its associated periodontal ligament (PDL) while opening the bite. The finite element model consisted of the mandibular teeth, the alveolar bone, and the PDL of the mandibular incisors. The clinical scenario was simulated by applying a force of 10 cN to the mandibular incisor in a crown-root direction. The von Mises stress in the incisor and its PDL were calculated. Results: An obvious stress concentration at the tip and at the top of the alveolar ridge of the mandibular central incisors was found. In the PDL, tensile strain was recorded in one-third of the cervical and middle regions, whereas compressive stress occurred on one-third of the apex and both the distal and labial sides of the PDL. This illustrates the difficulty in achieving the desired intrusive movement along the long axis of the tooth in a clinical setting. The highest stress concentration in the PDL was located at the cervical margin and declined steadily to the apex. The maximum stress was 20.5GPa at the alveolar crest. This study indicated that finite element modeling is a feasible and effective method for studying the open-bite technique. Areas subjected to greater stress may develop cell hyalinization within the ligament.

Finite element analysis, Open-bite, Periodontal ligament, The incisor, Von Mises stress.

Introduction

In orthodontics, tooth movements are produced by the reaction of cells in the periodontium while force is loaded on the crown of the teeth. The magnitude and distribution of the stress are the main effects for tooth movements. Opening the bite, which can be done by a number of methods, is a useful technique that is commonly used in clinical practice to treat deep overbite [1-3].

Over the last decades, numerical methods to calculate stress and strain fields in the periodontium have been extensively used, and the finite element (FE) method has frequently been the method of choice. The complexity of the shape and tissue composition of the dental region does, however, raise questions about the validity of results from some previous analyses and pose limitations on the scope of the FE simulation. For instance, FE simulations are often limited to simulations of orthodontic tooth movements for a single tooth [4,5]. Although many attempts to relate the force system to tooth displacement and the reaction of the surrounding tissues have been made, a clear relationship remains to be presented. This may be due to deficiencies in the applied methods or inaccurate values for properties of the modeled tissues. In this study we developed a comprehensive mechanical, 3- dimensional (3D), numerical model that consists of the mandibular teeth, the alveolar bone, and the PDL of the mandibular incisor. We simulated the clinical situation and investigated stress distribution in the mandibular central incisor and the PDL, while opening the bite with bent wire to explore a feasible and available method for treating deep overbite in the future.

Materials and methods

Models

The results of the FE analysis were found to largely depend on the accuracy of the model [6]. Therefore, the geometric information for the finite element model was based on a three-dimensional physical model consisting of 28 permanent plastic teeth (I21D-400, Nissin Dental Products, Shanghai, China). Since the morphological data derived from the plastic teeth model was in accordance with the morphological data of an Asian population, the resulting model would be representative. Moreover, each plastic tooth could be assembled independently, and it was therefore easy to scan and capture data. A 3D measuring apparatus (Real scan USB 200) was used to survey the alignment curve and teeth.

With a scanning accuracy of 0.005 mm, the mesial, distal, labial, lingual and occlusal surfaces were scanned in turn. The data was input to CATIA software, and this software was used to draw and mosaic the contour line on all levels before using a series of image processing techniques such as image refinment and smoothing to form tooth shape. After these treatment, the tooth size was changed slightly, and in order to get the universal standard dental data, corrections were made using standard data. The model was extracted from the FREEFOEM of the IDEAS software, then crown length, crown width, crown thickness, neck width, neck thickness, and root length of each tooth were measured. These measurements were compared to the statistical data of Huiyun Wang [7], and checked whether they were in the average range of the standard tooth. An overall correction was completed to guarantee the correct standard dental data and graphics.

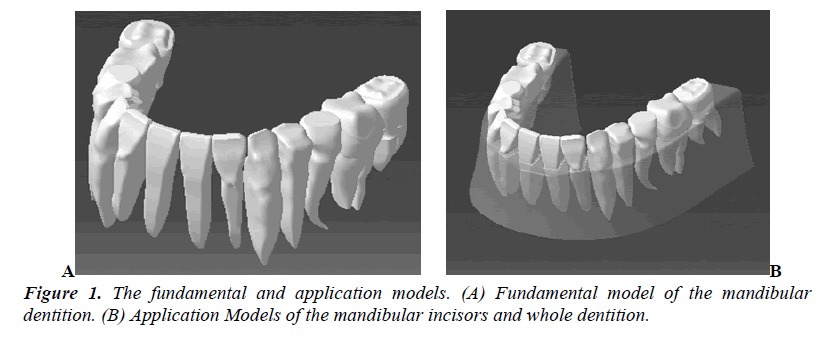
The 3D finite element model was constructed to include the dentition, the PDL, and alveolar bone, with good resemblance and computation. The fundamental and application models are displayed in Figure 1.

Preprocessing of the Three-Dimensional Element Model

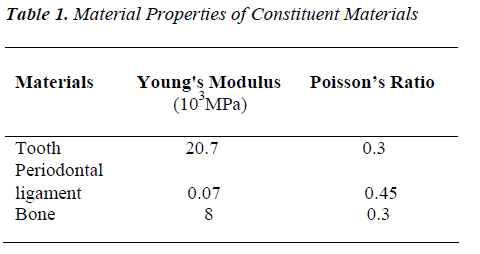
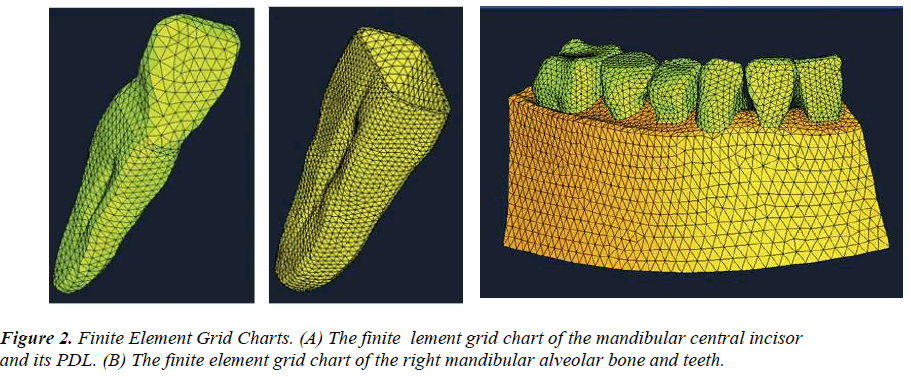
Preprocessing of the 3D element was organized into three parts: (i) parameter definition, (ii) model conversion, and (iii) construction of the mesh partitioning grid. Homogenous, isotropic, and linearly elastic behavior were assumed for all materials. The physical properties of the constituent materials composing the model were based on a review of the literature (Table 1) [8]. The hypermesh was used to divide the mesh and the automesh in two dimensions. The tetramesh in three dimensions was used to construct the 3D solid finite element model of the mandibular central incisor, the PDL, and alveolar bone (Figure 2).

Table 1. Material Properties of Constituent Materials

Table 2. The Loading Stress in Different Parts (10³MPa)

Elements and Nodes

Tetrahedral 3D elements were used. Four-node linear cells were used instead of 10-node quadratic elements, as the latter significantly complicates the computation of contact pressures. The model contained 60,319 nodes and 12,626 elements. There were 9848 nodes for the central incisor and 9870 for its PDL; 5789 for the lateral incisor and 7377 for its PDL; and 8412 for the alveolar bone.

Constraints and Loads

The material and organization of the model were assumed to be homogeneous, linear-elastic, isotropic, and continuous. The tooth was smooth with some physical mobility in the alveolus. The external constraints of the model were fixed and smooth. The thickness of the PDL was 0.25 mm. We also assumed that the contact point between two teeth was smooth. The interaction between teeth was achieved by dividing the grid, which was based on the public interface. Every cross-section of the model was not sliding mutually when moving. Each unit had sufficient stability between the various units.

The bottom and mesial sections of the alveolar bone were fully bound, whereas the labia and lingual surfaces of the alveolar bone were not bounded, as they are the free boundary surface.

In clinical practice, brackets are bound at a specific position on the tooth and engaged by bent wire in the brackets to create an acting force on the teeth equal to that on the brackets. To simulate the clinical situation, a force of 10 cN [9] was applied on the mandibular incisor in a crown-root direction. The point of force system application was 4 mm apical to the incisal edge, which is the same point where the bracket was bonded.

The PDL had an isotropic fibrous structure with a nonlinear stress-strain relationship [10]. The thickness of the PDL was different at various parts of the root [11]. These factors were included in recent calculations of the stress distribution in the PDL [12,13]. Therefore, it was assumed that the PDL should be a linear elastic film, and its thickness would be the same in all teeth. Although the PDL is a nonlinear visco-elastic material [14,15], most FE models incorporate linear elastic properties as pointed out by Cattaneo et al. [16]We used a similar approach in this study when considering force and stress, whereby the linear elastic properties of the PDL exhibit the same stiffness as the initial behavior of the nonlinear PDL [17].

The morphology of the alveolar structures was not assigned any specific value related to the load-transfer mechanism. As the connection of the root, the PDL and the alveolar bone form a flexible buffer system, and the root of the tooth was deep in alveolar bone, the tooth could be moved only slightly by orthodontic force. While the Young's Modulus of the tooth and alveolar bone are far bigger than that of the PDL, the displacement and deformation of the alveolar bone was assumed to be negligible. Therefore in the process of load analysis, the alveolar bone could be defined as a rigid foundation. We considered the alveolar bone a rigid boundary in order to meet the boundary constraints of the model.

Von Mises stress was calculated and presented in colored contour bands. Von Mises stress was selected because it represented the overall stress intensity.

Results

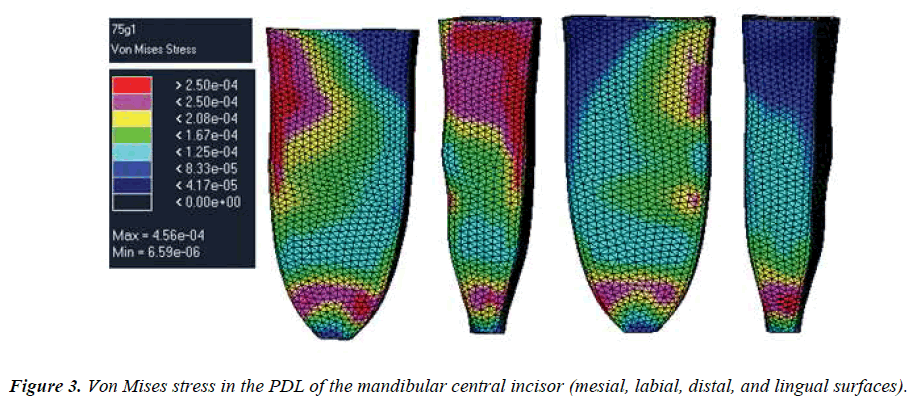
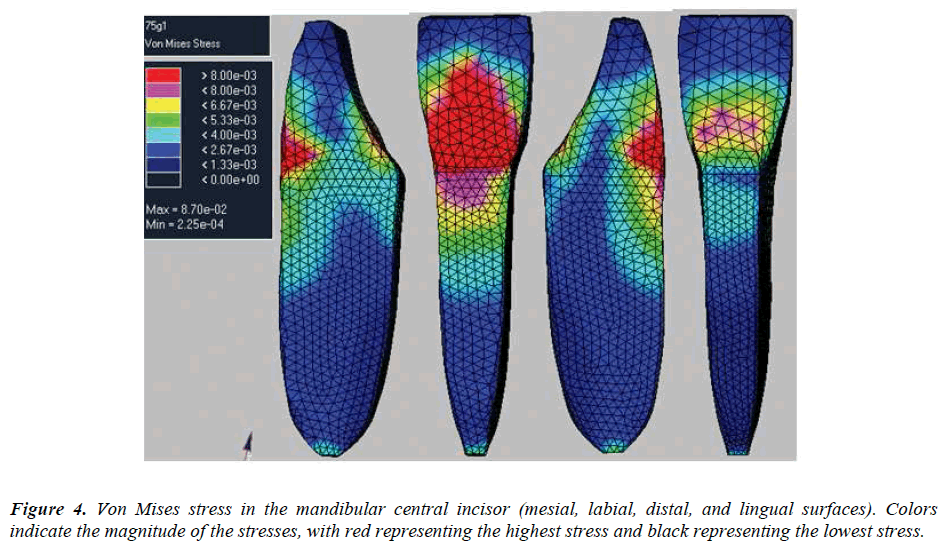
The results are summarized in Figures 3, Figure 4, and Table 2. The principal stresses at the same part of the PDL were a close approximation. They were conclusively tensile strength or compression stresses. On the labial surface, the stress changed from pull to compression steadily from the cervical part to the apex. The distribution on the lingual surface was opposite to that on the labial surface and coincided with the movement tendency of the tooth. The highest stresses in the PDL were found at the labial portion of the tooth.

Figure 1. The fundamental and application models. (A) Fundamental model of the mandibular dentition. (B) Application Models of the mandibular incisors and whole dentition.

Figure 2. Finite Element Grid Charts. (A) The finite lement grid chart of the mandibular central incisor and its PDL. (B) The finite element grid chart of the right mandibular alveolar bone and teeth.

Figure 3. Von Mises stress in the PDL of the mandibular central incisor (mesial, labial, distal, and lingual surfaces).

Figure 4. Von Mises stress in the mandibular central incisor (mesial, labial, distal, and lingual surfaces). Colors indicate the magnitude of the stresses, with red representing the highest stress and black representing the lowest stress.

Discussion

The PDL is a soft tissue, which is nonlinear, visco-elastic, anisotropic, and nonhomogeneous. To simplify the calculation, it has long been considered a homogeneous, elastic material [17]. In recent years, however, there has been progress with the biological simulation of the PDL [18]. Geramy et al. [19] modeled the PDL of the mesial, distal, labial, and lingual surfaces at different depths. Qian et al. [12] and Katona et al. [20] modeled the PDL as two kinds of material: a principal fiber (PF) and a nonprincipal fiber matrix (NPFM). Although they were configured as homogeneous and isotropic materials, only the PF bears tensile stress and does not transmit stress. Therefore, the PDL was considered as nonlinear, while the NPFM was considered viscoelastic.

In this study, we designed the PDL as a simple, linear, and elastic material. This was so that we could analyze the stress distribution of the tooth and its supporting tissues under an instantaneous load. The simulation was static. Although each surface of the PDL is of a different thickness and anisotropy, it was consistent with physiological conditions, but the exact material parameters of the PDL were difficult to obtain. The existing literature contains only a partial simulation for a single tooth [4,5]. It remains unclear whether this method could improve the accuracy of an analysis of multiple teeth. We refined the part that concerned us and simplified that which did not concern us for purposes of efficiency as complex calculations might cause an exponential increase in computing time.

The Reasons for Setting the Load Condition

This study examined the force system of the mandibular central incisor and its associated PDL while opening the bite, as deep overbite is a common condition and there are many methods to treat it in clinical practice. In the past, the flat bite plate was a commonly used and easy to learn procedure, appropriate for most cases. However, many patients reject the flat bite plate because of its influence on oral functioning and the success of this treatment depends entirely on patient cooperation. Therefore, clinician-scientists have sought methods for treating deep overbite merely with bending wires.

Current treatments of the bending-wire type include segmental archwire, horizontal or “T” loop archwire, rocking-chair archwire, and multi-loop edgewise archwire [1-3]. To evaluate the distribution of stress in the root of the central incisor and its PDL while using the archwires to open the bite, we defined the loading force as a force of 10 cN which was applied to the mandibular incisor in a crown-root direction. The point of force system application was 4 mm apical to the incisal edge (the same point where the bracket was bonded).

As in previous studies [21-25], the PDL was modeled as a 0.25-mm layer of uniform thickness and was treated as linear elastic and isotropic, even though the PDL exhibits anisotropy and nonlinear viscoelastic behavior because of tissue fluids [26]. The tooth was simplified as a homogeneous body with rough tips, because the force transmitted to the PDL was not significantly affected by adding the internal and external tooth structure.

Analysis of the Results.

The magnitude and distribution of the stress in the periodontium were the predominant causes for tooth movements [27]. In this research, stress distribution in the mandibular central incisor, PDL, and associated alveolar bone were studied. In the finite element model, the highest stress concentration in the PDL was located at the cervical margin. This might be because the orthodontic force was applied to the buccal bracket of each tooth.

Resorption might take place in the cementum under orthodontic force and might even involve the dentine. Therefore, applied force and moment magnitudes must be reduced in proportion in order to maintain physiologically tolerable movements without further damage to these supporting structures.

Maximal strains in the PDL occur at the alveolar crest and the root apex; these sites have the greatest deformation and rates of bone remodeling. Clinically, moderate peak strains around the center of resistance of the tooth are desired to prevent orthodontically induced root resorption [28].

Future Problems

In the future, additional modeling may be needed along with a time-dependent finite element analysis. It should be noted that this theoretical study, which has no empirical basis for clinical application, involved many assumptions. The current findings may have to be changed if the assumptions are unrealistic. Therefore, the resultant values should be interpreted only as a reference to aid clinical judgment.

Conclusion

This study indicated that finite element modeling is a feasible and effective method for studying the open-bite technique. We found that the von Mises stress in the PDL declined steadily from the cervical part to the apex. The maximum stress occurred at the cupular part of the socket ridge. Hydrostatic stresses in the PDL can be used as markers for predicting the potential sites of root resorption. This is the area where one might expect greater stress, leading to potential cell hyalinization within the ligament.

Acknowledgments

This work was supported by Heilongjiang Provincial Department of Education-funded project (No. 12511219).

Conflict of interest

The authors declare that they have no conflict of interest.

References

1. Shroff B, Lindauer SJ, Burstone CJ, et al. Segmented approach to simultaneous intrusion and space closure: biomechanics of the three-piece base arch appliance. Am J Orthod Dentofacial Orthop 1995; 107: 136-143.
2. Chen L, Zhang D, Fu MK, et al. The three-dimensional nonlinear finite element analysis of force system of the ?rocking-chair archwire?. Zhonghua Kou Qiang Yi Xue Za Zhi 2004; 39: 239-241.
3. Shao P, Yan WJ, An JT. Clinical effects of biteopening by use of multi-loop edgewise arch wire. Huaxi Kou Qiang Yi Xue Za Zhi 2006; 24:561-562.
4. Bourauel C, Vollmer D, Jager A. Application of bone remodeling theories in the simulation of orthodontic tooth movements. J Orofac Orthop 2000; 61: 266-279.
5. Schneider J, Geiger M, Sander FG. Numerical experiments on long-time orthodontic tooth movement. Am J Orthod Dentofacial Orthop 2002; 121: 257-265.
6. Armitage GC. Development of a classification system for peri-odontal diseases and conditions. Ann Periodontol 1999; 4: 1- 6.
7. Wang HY. Measurement of human teeth and statistics. Zhonghua Kou Qiang Yi Xue Za Zhi 1959; 3: 149-52.
8. McGuiness NJP, Wilson AN, Jones ML, et al. A stress analysis of the periodontal ligament under various orthodontic loadings. Eur J Orthod 1991; 13: 231-242.
9. William R, Henry W, William R Proffit, et al. Fields & David M. Sarver. In: Mosby Contemporary orthodontics. 2007; 304.
10. Toms SR, Lemons JE, Bartolucci AA, et al. Nonlinear stress-strain behavior of periodontal ligament under orthodontic loading. Am J Orthod Dentofacial Orthop 2002; 122: 174-179.
11. Coolidge ED. The thickness of the human periodontal membrane. Am J Dent Assoc Dent Cosmos 1937; 24: 1260-1270.
12. Qian H, Chen J, Katona TR The influence of PDL principal fibers in a 3-dimensional analysis of orthodontic tooth movement. Am J Orthod Dentofacial Orthop 2001; 120: 272-9.
13. Toms SR, Eberhardt AW. A nonlinear finite element analysis of the periodontal ligament under orthodontic tooth loading. Am J Orthod Dentofacial Orthop 2003; 123: 657-665.
14. Verna C, Dalstra M, Lee TC, et al. Microcracks in the alveolar bone following orthodontic tooth movement: a morphological and morphometric study. Eur J Orthod 2004; 26: 459-467.
15. Nagaraja S, Couse TL, Guldberg RE. Trabecular bone microdamage and microstructural stresses under uniaxial compression. J Biomech 2005; 38: 707-716.
16. Cattaneo PM, Dalstra M, Melsen B. The finite element method: a tool to study orthodontic tooth movement. J Dent Res 2005; 84: 428-433.
17. Andersen KL, Pedersen EH, Melsen B. Material parameters and stress profiles within the periodontal ligament. Am J Orthod Dentofacial Orthop 1991; 99: 27-44.
18. Middleton J, Jones M, Wilson A. The role of the periodontal ligament in bone modeling: The initial development of a time-dependent finite element model. Am J Orthod Dentofacial Orthop 1996; 109: 155-162.
19. Geramy A. Alveolar bone resorption and the center of resistance modification (3-D analysis by means of the finite element method). Am J Orthod Dentofacial Orthop 2000; 117: 399-405.
20. Katona TR, Qian H. A mechanism of noncontiguous supraosseous tooth eruption. Am J Orthod Dentofacial Orthop 2001; 120: 263-271.
21. Tanne K, Nagataki T, Inoue Y, et al. Patterns of initial tooth displacements associated with various root lengths and alveolar bone heights. Am J Orthod Dentofacial Orthop 1991; 100: 66-71.
22. Tanne K, Koenig HA, Burstone CJ Moment to force ratios and the center of rotation. Am J Orthod Dentofacial Orthop 1988; 94: 426-431.
23. Cobo J, Sicilia A, Arguelles J, et al. Initial stress induced in periodontal tissue with diverse degree of bone loss by an orthodontic force: tridimensional analysis by means of the finite element method. Am J Orthod Dentofacial Orthop 1993; 104: 448-454.
24. Cobo J, Arguelles J, Puente M, et al. Dentoalveolar stress from bodily tooth movement at different levels of bone loss. Am J Orthod Dentofacial Orthop 1996; 110: 256-262.
25. Jeon P, Turley P, Moon H, et al. Analysis of stress in the periodontium of the maxillary first molar using a three-dimensional finite element model. Am J Orthod Dentofacial Orthop 1999; 115: 267-274.
26. Middleton J, Jones M, Wilson A. Role of the periodontal ligament in bone modeling: the initial development of a time-dependent finite element model. Am J Orthod Dentofacial Orthop 1996; 109: 155-162.
27. Graber TM, Swain BF. Current principles and techniques. St. Louis: Mosby Co. 1975; 101-119.
28. Brudvik P, Rygh P. Non-clast cells start orthodontic root resorption in the periphery of hyalinized zones. Eur J Orthod 1993; 15: 467-480.