Editorial - Archives of General Internal Medicine (2019) Volume 3, Issue 1
Relationship of Leptin with Glucose, BMI, Age, Insulin and Breast Cancer Biomarkers
Rabindra Nath Das1,2*, Youngjo Lee2
1Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India
2Department of Statistics, College of Natural Science, Seoul National University, Seoul, 151-747, Korea
- *Corresponding Author:
- Rabindra Nath Das
Department of Statistics
The University of Burdwan
Burdwan, West Bengal, India
E-mail: rabin.bwn@gmail.com
Accepted date: February 28, 2019
Citation: Das RN, Lee Y. Relationship of leptin with glucose, BMI, age, insulin and breast cancer biomarkers. Arch Gen Intern Med. 2019;3(1):01-03. Doi: 10.4066/ 2591-7951.1000e010
Editorial
Breast cancer is frequently observed throughout the world as the second cause of cancer-related death in women [1,2]. Young women with higher body mass index (BMI) may have a greater risk of breast cancer [3-11]. In addition, obese individuals have a greater risk of diabetes also [4-9]. Again, they have unusually high leptin levels, as for some of them, the brain does not respond to leptin, so they keep eating despite excessive fat stores, which is known as leptin resistance. Naturally, the following queries arise for scientific investigation. What is the relation of leptin with BMI, age, glucose, insulin and breast cancer biomarkers? What are the associations of leptin with these factors? What are the roles of leptin on these factors? The present note examines these queries based on real data set.
For a multivariate data set, generally associations of a factor with other covariates can only be obtained by suitable probabilistic modeling. Herein the taken data set is a multivariate data, which is given in UCI Machine Learning Repository. The data set contains 116 (52 healthy controls and 64 patients) women containing 10 study variables, and the data description is given in [12]. The data set contains the following factors.
*Age (years),
* BMI (kg/m2),
* Insulin (μU/mL),
* Glucose (mg/dL),
* Resistin (ng/mL),
* MCP-1 (pg/dL),
* Leptin (ng/mL),
* Adiponectin (μg/mL),
* HOMA,
* Types of subjects (1=healthy controls; 2=patients).
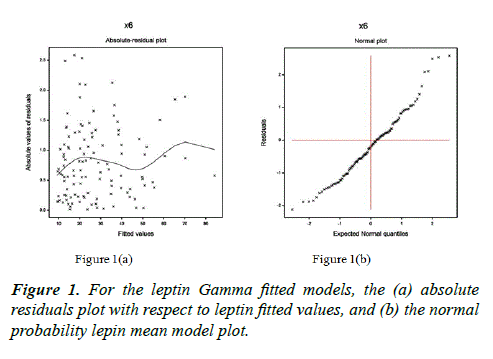
Note that the data set contains glucose and insulin as diabetes marker, and resistin, MCP-1, adiponectin, leptin and HOMA as breast cancer biomarkers. The response leptin is positive, continuous and heteroscedastic, which can be modeled by any appropriate transformation, if it is stabilized under that transformation. But the response leptin is not stabilized by any appropriate transformation. So, it can be modeled by joint generalized linear models (JGLMs) with Log-normal and Gamma distributions [13,14]. Final model is selected based on the lowest Akaike information criterion (AIC) value (within each class), which minimizes both the squared error loss and predicted additive errors [15-18]. Herein the response leptin is modeled using JGLMs with both Log-normal (AIC=869.84) and Gamma (AIC=869.78) distribution. But based on AIC rule, both the distributions give identical results. Again the final model is verified by model checking diagnostic plots such as absolute residuals and normal probability plots in Figure 1. Figure 1a shows the absolute residuals plot which is almost flat diagram with the running means, concluding that variance is constant with the running means. In addition, normal probability plot in Figure 1b does not indicate any lac of fit. So, both the plots reveal that the final fitted leptin model is an approximately a true model of it. The relationship of leptin is given by the following two of its mean and variance equations. The final Gamma fitted Leptin mean ( μˆ ) model is μˆ =exp(-0.227+0.092 BMI+0.006 Glucose+0.010 Insulin+0.025 Adiponectin+0.016 Resistin–0.001 MCP.1–0.001 Adiponectin*Resistin), and Gamma fitted Leptin variance (σˆ2 ) model is σˆ2 =exp(- 3.809+0.042 Age+0.153 Resstin–0.003 Age*Resistin).
The above two models concludes the following.
• Mean leptin is highly directly associated with BMI (p<0.0001), inpreting that BMI rises as leptin increases.
• Mean leptin is directly associated with glucose (p=0.0135), indicating that leptin increases as glucose increases.
• Mean leptin is directly associated with insulin (p=0.0557), implying that leptin increases as insulin increases.
• Mean leptin is directly associated with adiponectin (p=0.0254), interpreting that leptin increases as adiponectin increases.
• Mean leptin is directly associated with resistin (p=0.0027), indicating that leptin increases as resistin increases.
• Mean leptin is inversely associated with MCP.1 (p=0.0213), implying that leptin increases as MCP.1 decreases.
• Mean leptin is inversely associated with the interaction effect Adiponectin*Resistin (p=0.0966), concluding that leptin increases as the joint effect Adiponectin*Resistin decreases. Note that both the marginal effects adiponectin and resitin are positively associated with leptin, while their joint interaction effect is negatively associated.
• Variance of leptin is directly associated with age (p=0.0034), indicating that leptin variance is higher at older ages than younger.
• Variance of leptin is directly associated with resistin (p=0.0028), concluding that leptin variance increases as resistin increases.
• Variance of leptin is inversely associated with the interaction effect age*resistin (p=0.0009), implying that leptin variance increases as the effect age*resistin decreases. Note that both the marginal effects age and resistin are positively associated with leptin variance, while their joint effect is negatively associated.
The summarized form of the above associations of leptin is displayed in Table 1. From the above, it is observed that leptin is associated with both the diabetes markers such as glucose and insulin. In addition it is associated with adiponectin, resistin, MCP-1 and interaction effect adiponectin*resistin. It is highly associated with BMI also. There is no association between leptin and HOMA.
| Response | Associated with | Types of association | p-value |
|---|---|---|---|
| Leptin mean | BMI | Positive | <0.0001 |
| Glucose | Positive | 0.0135 | |
| Insulin | Positive | 0.0557 | |
| Adiponectin | Positive | 0.0110 | |
| Resistin | Positive | 0.0073 | |
| MCP-1 | Negative | 0.0330 | |
| Adiponectin*Resistin | Negative | 0.0966 | |
| Leptin variance | Age | Positive | 0.0034 |
| Resistin | Positive | 0.0028 | |
| Age*Resistin | Negative | 0.0009 |
Table 1. Associations of leptin with age, BMI, diabetes and breast cancer biomarkers.
The report focuses the associations of leptin with glucose age, insulin, BMI and breast cancer biomarkers through probabilistic modeling of its mean and variance. Final model has been selected based on lowest AIC value and model checking plots. The current mean and variance models of leptin focus many interesting associations with many diabetes and breast cancer biomarkers, which have not been reported in any earlier articles. Medical practitioners and researchers will be benefitted from the report. It is shown herein that higher leptin levels invite many diseases such as diabetes and breast cancer. Every individual should care on leptin levels.
Conflict of Interest
The authors confirm that this article content has no conflict of interest.
Acknowledgement
This research was supported by the Brain Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (2014M3C7A1062896).
References
- Williams CL, Hayman LL, Daniels SR, et al. Cardiovascular health in childhood: A statement for health professionals from the Committee on Atherosclerosis, Hypertension, and Obesity in the Young (AHOY) of the Council on Cardiovascular Disease in the Young, American Heart Association. Circulation. 2002;106:143-60.
- US Dept Health and Human Services. The Surgeon General’s Call to Action to Prevent and Decrease Overweight and Obesity. Rockville, MD: US Department of Health and Human Services, Public Health Service, Office of the Surgeon General 2001.
- National Institutes of Health. Clinical guidelines on the identification, evaluation, and treatment of overweight and obesity in adults-the evidence report. Obes Res. 1998;6(suppl 2):51-209S.
- Gunter MJ, Xie X, Xue X, et al. Breast Cancer Risk in Metabolically Healthy but Overweight Postmenopausal Women. Cancer Res. 2015;75(2):270-74.
- Bays HE, Chapman RH, Grandy S. The relationship of body mass index to diabetes mellitus, hypertension and dyslipidaemia: comparison of data from two national surveys. Int J Clin Pract. 2007;61:737-47.
- Jarde T, Perrier S, Vasson MP, et al. Molecularmechanisms of leptin and adiponectin in breast cancer. Eur J Cancer. 2011;47:33-43.
- Ray A, Cleary MP. Leptin as a potential therapeutic target for breastcancer prevention and treatment. Expert OpinTher Targets. 2010;14:443-51.
- Paz-Filho G, Lim EL, Wong ML, et al. Associations between adipokines and obesity-related cancer. Front Biosci. 2011;16:1634-50.
- Das RN, Lee Y. Association of Serum Adiponectin with Age, BMI and Other Breast Cancer Biomarkers. J Blood Lymph. 2018;8:233.
- Feng Z, Zhang H. Resistin and Cancer Risk: A Mini-Review. EndocrinolMetabol Syndrome. 2011;S4:003.
- Yang RZ, Huang Q, Xu A, et al. Comparativestudies of resistin expression and phylogenomics in human and mouse. Biochem Biophys Res Commun. 2003;310:927-35.
- Patrício M, Pereira J, Crisóstomo J, et al. Using Resistin, glucose, age and BMI to predict the presence of breast cancer. BMC Cancer. 2018;18:18-29.
- Lee Y, Nelder JA, Pawitan Y. Generalized Linear Models with Random Effects (Unified Analysis via H–likelihood). Second Edition, London: Chapman & Hall 2017.
- Qu Y, Tan M, Rybicki L. A unified approach to estimating association measures via a joint generalized linear model for paired binary data. Communications in Statistics-Theory and Methods. 2000;29:143-56.
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning, Second Edition, Springer-Verlag, 2009.