Biomedical Research

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.
Reach Us +44-7360-538437

Research Article - Biomedical Research (2016) Computational Life Sciences and Smarter Technological Advancement

Image reconstruction using compressed sensing for individual and collective coil methods

Mahmood Qureshi*, Muhammad Junaid, Asadullah Najam, Daniyal Bashir, Irfan Ullah, Muhammad Kaleem and Hammad Omer

COMSATS Institute of Information Technology, Pakistan

*Corresponding Author:
Mahmood Qureshi
COMSATS Institute of Information Technology, Pakistan

Accepted March 07, 2016

Visit for more related articles at Biomedical Research

Abstract

Introduction: Compressed Sensing (CS) has been recently proposed for accelerated MR image reconstruction from highly under-sampled data. A necessary condition for CS is the sparsity of the image itself in a transform domain. Theory: Sparse data helps to achieve incoherent artifacts, whichcan be removed easily using various iterative algorithms (for e.g. non-linear Conjugate Gradient) as part of CS. The image should be reconstructed by a non-linear algorithm that enforces both the sparsity of the image representation and consistency of the reconstruction with the acquired samples. Methods: This work presents the results obtained by applying CS on non-Cartesian k-space data acquired using highly under-sampled Radial and Spiral schemes. The CS reconstruction is performed using Individual Coil Method (ICM) and Collective Coil Method (CCM). The ICM approach considers the under-sampled data from each coil individually whereas CCM considers under-sampled data from the coils collectively for the reconstruction of the MR images. Results and Conclusion: Artifact Power (AP) and SNR are used as quantifying parameters to compare the quality of the reconstructed images. The results show that radial trajectory is a suitable choice for the CS in MRI. In terms of the method compatibility,ICM shows promising results.

Keywords

Compressed sensing, MRI.

Introduction

Recent advancements in the field of MR imaging are significant. Despite having numerous advantages over other imaging modalities, a drawback of MRI is its time consuming data acquisition process. Magnetic Resonance Imaging (MRI) is a non-invasive, non-ionizing medical imaging modality [1]. MR image is acquired by first placing the patient under a strong magnetic field and then applying the Radio Frequency (RF) pulses along with the application of the Phase Encode Gradient (GPE) and Frequency Encode Gradient (GFE). The size of the image decides how many times the RF pulse needs to be applied, hence making the MRI scan a time consuming process [2].

CS has been recently proposed to accelerate the MR data acquisition process [3,4]. CS complements MR imaging because many MR images are already sparse or can be made sparse using some sparsifying transform [5] (e.g. wavelet transform, finite difference etc.). Further acceleration can be achieved for CS by acquiring the under-sampled data along non-Cartesian schemes, which is the main focus of this paper.

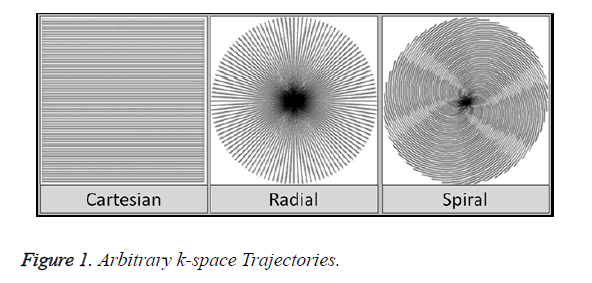
There are many data acquisition schemes in MRI. Variable Density (VD) [6] Random under-sampling is one good option for quality reconstruction using CS for Cartesian, Radial and Spiral trajectories [7]. In an image most of the information is located at the center of the k-space. Variable Density random under-sampling complements this data arrangement as it focuses on extracting information from the center rather than the borders of the k-space; hence VD-Cartesian, Spiral and Radial trajectories [8] are used for CS reconstruction in this work.

The aim of this paper is to investigate the performance of CS for highly under-sampled Variable Density Cartesian (VDCartesian), Spiral and Radial trajectories. The data acquired through non-Cartesian k-space trajectories can contribute towards motion robustness and rapid imaging [9].

Theory

Compressed sensing (CS)

The general approach in data handling for imaging is to collect data and then compress it. Putting it the other way around, collecting compressed data at the time of acquisition is what CS does. One of the many solutions to engineer potential scan time reductions is to apply the CS technique to MRI.

Some necessary conditions for CS to be applicable are [10]:

The image itself should be sparse in a transform domain Sampling should be incoherent (providing incoherent artifacts) Non-linear algorithm for reconstruction

Sparsity is the number of non-zero pixels present in the data. Non-zero pixels representing relevant information scattered throughout the image make CS more applicable. Incoherent sampling accounts for incoherent artifacts which are easier to remove as compared to coherent artifacts [4]. The image should be reconstructed by a non-linear algorithm that enforces both the sparsity of the image representation and consistency of the reconstruction with the acquired samples.

The conventional unconstrained equation used for CS in the so called Lagrangian form [10] is:

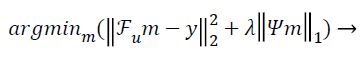image (1)

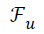Where image is the under-sampled Fourier operator, m is the estimated vector, is the measured k-space data from the scanner, λ being the regularization parameter and ψ the sparsifying operator. Image sparsity can be enhanced either by any sparsifying operator, or by subtracting/adding prior to image estimation, or both [10]. The sparsifying transform used in this paper is the finite difference transform usually referred as Total Variation (TV) [11]. TV is the finite difference between two consecutive rows and columns for a single line of matrix [12].

Trajectories

Exploring data acquisition in MRI using non-Cartesian trajectories is a viable research option as it has many advantages over the uniform-Cartesian data (Figure 1). The kspace area is well utilized, focusing essential information at the center allowing to ignore the areas on the boundary. Scan time is also significantly reduced as more phase encoding lines are skipped using non-Cartesian data [13,14].

biomedres-Arbitrary-k-space-Trajectories

Figure 1. Arbitrary k-space Trajectories.

The data along non-Cartesian trajectories is interpolated through Non-Uniform Fast Fourier Transform (NUFFT) using Min-Max Interpolation. The Min-Max approach provides lower approximation error than conventional interpolation error [15,16].

Gridding

The image reconstruction using non-Cartesian data is slow as compared to Cartesian data because the data is non-uniform in the k-space and we cannot apply fast Fourier transform to nonuniform data. To speed the reconstruction process gridding is used [17,18]. The main idea of gridding is to map the non- Cartesian data onto a rectilinear grid using a convolution kernel and then compensating for the convolution using an image deapodization function [9,19].

An integral part of gridding is the density compensation procedure. Unlike uniform Cartesian k-space trajectories, non- Cartesian k-space trajectories are not uniform, thus evaluating all the points as equal functions while reconstructing the data can result in major artifacts. An ideal way to perform density compensation is the post-compensation approach where we keep track of the k-space energy at each point and then divide by the particular energy after convolution [7]. But this approach is only possible if the energy is varying slowly in the data. Usually this approach doesn’t work for a majority of the k-space trajectories as it doesn’t work well with the image deapodization step [20].

The other more viable option for performing density compensation is the pre-compensation approach where density compensation is performed prior to convolution. The density of every point is measured by using a density compensation function (DCF). Many of these functions are already available and can be designed as per requirement. A simple calculation of the voronoi diagram [9] of the sample distribution is used here (this works well for most of the general trajectories). The pre-compensation technique has been adopted for the work presented in this paper.

Convolution is then performed using a pre-defined kernel function; the usual choice is the Kaiser- Bessel function [9]. The transform of the gridding kernel should be known in order to do deapodization, whichis a point-to-point multiplication of the image with the inverse of the transform kernel in order to minimize the error caused by convolution.

Methods

CS image reconstruction algorithm

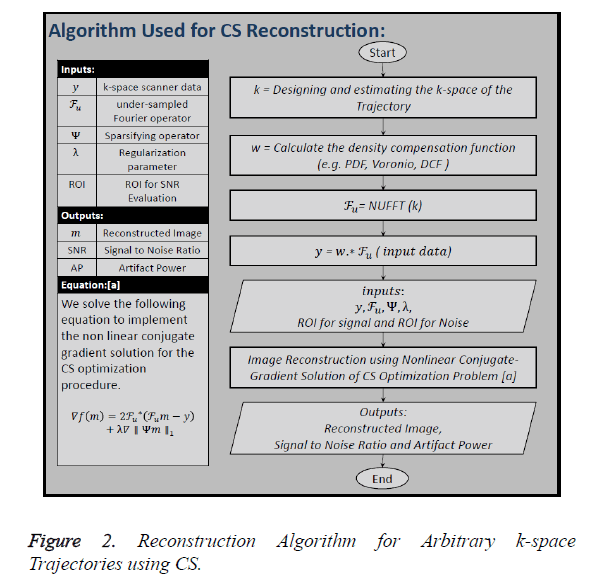
Figure 2 shows all the steps of the CS reconstruction process used in this paper. The first step is to design the k-space of the trajectory (k) under consideration. In the second step the Density Compensation Function (DCF) () is calculated because we have used non-Cartesian trajectories, so the density of the k-space samples varies throughout the data. 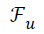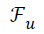Third step includes the calculation of under-sampled Fourier Operator (image) by taking the non-Uniform Fast Fourier Transform (NUFFT) of the trajectory designed in the first step. 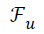In the next step undersampled, density compensated data () is calculated by convolving ‘w’ with ‘image’. The inputs to the algorithm are the under-sampled data (), under-sampled Fourier Operator (image), Sparsifying Operator (here TV is used as the Sparsifying operator), Regularization Parameter (α or λ) and to calculate SNR certain area for signal and noise should be declared [21].

biomedres-Algorithm-Arbitrary-k-space

Figure 2. Reconstruction Algorithm for Arbitrary k-space Trajectories using CS.

In this paper, the image is reconstructed using Non-Linear Conjugate Gradient Solution [10] for CS optimization problem, which uses the following equation:

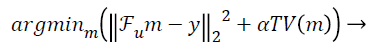image (2)

Image reconstruction algorithm using CCM and ICM

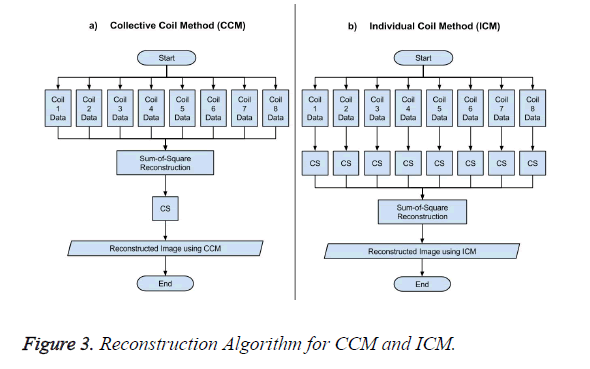
The data acquisition for CS is performed using multiple receiver coils. There are two ways to reconstruct the MR image in CS from the under-sampled data. One approach is to take the acquired under-sampled data from all the receiver coils and applying the sum-of-squares method to have a composite image, and then applying the CS algorithm to this composite image for reconstruction as shown in Figure 3a, this method is named as Collective Coil Method (CCM) in this paper. The other technique is to consider each under-sampled coil data individually for reconstruction, then applying the sum-ofsquares method to the individually reconstructed images to obtain a final result as shown in Figure 3b; this method is named as Individual Coil Method (ICM) in this paper.

biomedres-Algorithm-CCM-ICM

Figure 3. Reconstruction Algorithm for CCM and ICM.

MR experiments

Fully sampled data is acquired using eight channel receiver coils in uniform Cartesian form. The Scan parameters used for acquiring this human head data (1.5T and 3T) are: TE=10msec, TR=500msec, FOV=20cm, Bandwidth=31.25 KHz, Slice Thickness=3mm, Flip Angle=50 degrees, Matrix Size=256x256x8. This uniform Cartesian k-space data is transformed into VD-Cartesian, Radial and Spiral trajectories and then these trajectories are under-sampled for various acceleration factors (2X, 4X, 6X, 8X, 10X).

Complex white noise (SD (σ)=0.004) is added to every data set prior to reconstruction. At different acceleration factors, the number of projections for radial trajectory vary by a factor under consideration (e.g. at 2x the total projections (256) are under-sampled by a factor of 2 etc.). The spiral trajectory used is multi-shot, the number of shots being 41 and each shot being rotated by an angle of 2π/N (where N is the number of shots).

Evaluation of reconstruction

This paper uses two quantifying parameters i.e. Artifact Power (AP) and Signal-to-Noise Ratio (SNR) to judge the quality of reconstruction.

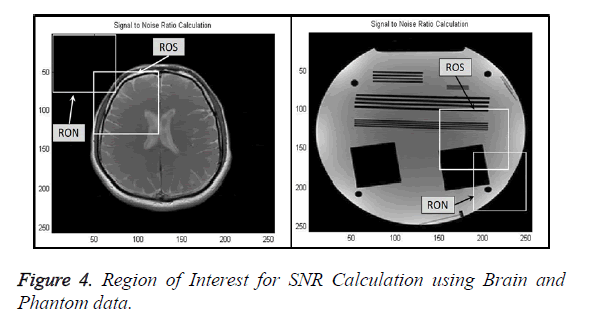
Signal-to-Noise Ratio (SNR): A Region-of-Interest for Signal (ROS) and Region-of-Interest for Noise (RON) is selected as shown in Figure 4. SNR is calculated by using the following formula [22,23]:

biomedres-Region-Interest-SNR

Figure 4. Region of Interest for SNR Calculation using Brain and Phantom data.

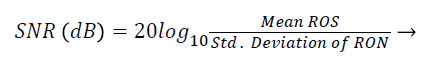image (3)

Artefact power (AP): AP is the difference between the original reference image and the reconstructed image. The concept of AP has been derived from ‘‘Normalized Sum of Square Difference Error’’. The AP in the reconstructed image is calculated on the basis of the reference image (Original Image). AP can be calculated using the following formula [22,23]:

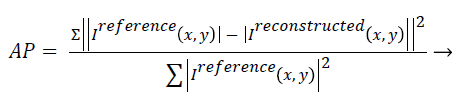image (4)

In the above formula, if 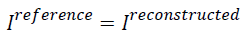image then AP will be zero which tells that there is no difference between the reference image and the reconstructed image. Similarly, if the AP value is bigger it means there is a considerable difference between the reconstructed image and the reference image. So for better image the AP should be less.

Results

Reconstruction using CCM (1.5 Tesla Head Data)

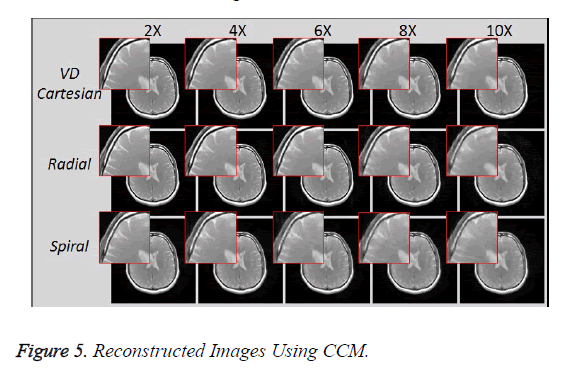
Figure 5 shows the reconstructed images, using Collective Coil Method (CCM), taken at different acceleration factors using various k-space trajectories where the acceleration factor varies vertically and the k-space trajectories are shown horizontally for the reconstructed images.

biomedres-Images-Using-CCM

Figure 5. Reconstructed Images Using CCM.

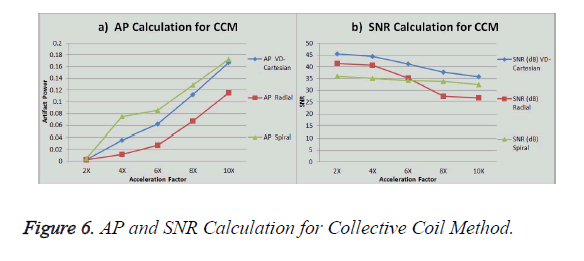
The graph in Figure 6a shows the AP (artifact power) for VDCartesian, Radial and Spiral trajectories, whereas in Figure 6b SNR is shown for these trajectories using Collective Coil Method. The diamond (blue) represents the trend for VDCartesian, square (red) for Radial and triangle (green) for the Spiral trajectories.

biomedres-AP-SNR-Calculation

Figure 6. AP and SNR Calculation for Collective Coil Method.

Reconstruction using ICM (1.5 Tesla Head Data)

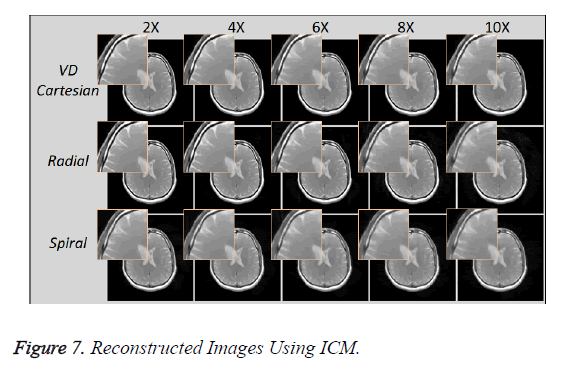
Figure 7 shows the reconstructed images, using Individual Coil Method (ICM), taken at different acceleration factors using various k-space trajectories where the acceleration factor varies vertically and the k-space trajectories are shown for the reconstructed images along horizontal lines.

biomedres-Images-Using-ICM

Figure 7. Reconstructed Images Using ICM.

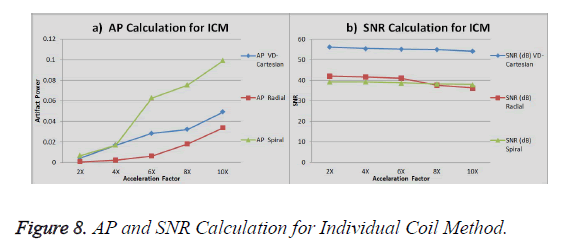
The graph in Figure 8a shows the AP (artifact power) for VDCartesian, Radial and Spiral, whereas in Figure 8b the SNR is shown for these trajectories using Individual Coil Method. The diamond (blue) represents the trend for VD-Cartesian, square (red) for Radial and triangle (green) for the Spiral trajectories.

biomedres-AP-SNR-Calculation

Figure 8. AP and SNR Calculation for Individual Coil Method.

Comparison CCM vs. ICM (3Tesla Head Data)

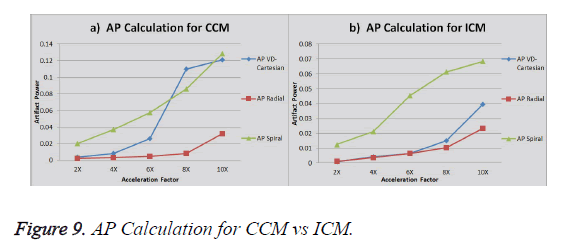
The graph in Figure 9a shows the AP (artifact power) for VDCartesian, Radial and Spiral trajectories using Collective Coil Method (CCM). The graph in Figure 9b shows the same using Individual Coil Method (ICM). The diamond (blue) represents the trend for VD-Cartesian, square (red) for Radial and triangle (green) for the Spiral trajectories.

biomedres-AP-Calculation-CCM-ICM

Figure 9. AP Calculation for CCM vs ICM.

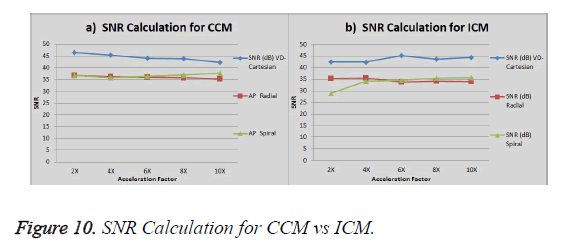
The graph in Figure 10a shows the SNR (Signal to Noise ratio) for VD-Cartesian, Radial and Spiral trajectories using Collective Coil Method (CCM). The Figure 10b shows the same using Individual Coil Method (ICM). The diamond (blue) represents the trend for VD-Cartesian, square (red) for Radial and triangle (green) for the Spiral trajectories.

biomedres-SNR-Calculation-CCM-ICM

Figure 10. SNR Calculation for CCM vs ICM.

Comparison CCM vs. ICM (1.5 Tesla Phantom Data)

The Figure 11 shows that the proposed method retains the high resolution features in the reconstructed image using ICM. The results have been obtained at different acceleration factors using various k-space trajectories.

biomedres-factor-different-trajectories

Figure 11. Shows the reconstructed image of 1.5T phantom image by varying the acceleration factor for different trajectories.

Discussion

Image reconstructions are performed by implementing CS algorithm on Individual Coil Method (ICM) and Collective Coil Method (CCM) on the under-sampled VD-Cartesian, Radial and Spiral trajectories. Three different data sets (1.5T Human Brain, 3T Human Brain and 1.5T Phantom) are used to test the results for the proposed methods. The data set acquired by the 3T MR scanner provides better results in terms of AP for both methods (CCM and ICM) as compared to the data set of 1.5T scanner. In terms of SNR 1.5T human brain data provides better results as compared to 3T scanner data for ICM but for CCM the results are opposite i.e. 3T scanner data gives better output.

CS for Radial trajectory provides better results i.e. it gives smaller Artifact Power (AP) for both ICM and CCM. It performs better than variable density Cartesian. In terms of SNR, VD Cartesian trajectory outperforms both the Spiral and Radial trajectories. If we compare AP and SNR of the results generated by the two reconstruction methods, ICM provides better results in terms of AP and SNR (it gives low values for AP and higher values of SNR).

A generalization of which non-Cartesian trajectory is superior cannot be justified because certain trade-off factors are present with respect to the quantifying parameters considered but it can be safely concluded from this work that radial trajectory is a suitable choice for the CS in MRI. In terms of the method compatibility ICM shows promising results. Further work should be done in order to explore the compatibility of other non-Cartesian trajectories for CS in MRI reconstruction.

References

Get the App