Research Article - Biomedical Research (2018) Computational Life Sciences and Smarter Technological Advancement: Edition: II
Higher order neural networks based on bioinspired swarm intelligence optimization algorithm for multimodal tumor data analysis
Deepa M*, Rajalakshmi M and Nedunchezhian R
Department of Computer Science and Engineering and Information Technology, Coimbatore Institute of Technology, Coimbatore, Tamil Nadu, India
- *Corresponding Author:
- Deepa M
Department of Computer Science and Engineering and
Information Technology
Coimbatore Institute of Technology, India
Accepted on June 06, 2017
DOI: 10.4066/biomedicalresearch.29-17-662
Visit for more related articles at Biomedical ResearchAbstract
Diagnosing tumor at early stages is very critical for treatment and understanding the disease pathogenesis. Analyzing and detecting tumor earlier helps us in deciding the course of actions for therapy. But analyzing multimodal cancer data and its sub-types is a very difficult and sensitive task and need classification methods with high accuracy. Also the data may be nonlinear and time sensitive. Hence a higher order neural network models called Pi-Sigma artificial neural network and functional link artificial neural network based on glowworm swarm optimization algorithm is proposed for dealing with multimodal cancer data. The performance of the proposed methods is tested with data from publicly available domains and the results show that the higher order neural networks with glowworm swarm optimization performs better than conventional neural network.
Keywords
Higher order neural network, Functional link neural network, Pi-sigma neural network, Glowworm swarm optimization, Multi-modal cancer data.
Introduction
Classification of data is an important data mining task. The main goal of a classification process is to predict the class label for each data in the given set. Various classification methods are available like support vector machines, decision trees, neural networks. Among these classifiers neural networks have gained huge success in recent years. There are different types of neural networks like Feed forward networks, recurrent neural network, Probabilistic neural network, Autoencoders, high order neural networks [1-5]. Among these types, high order networks like Pi-Sigma network (PSNN) [6,7], functional link artificial neural network (FLANN) have the capacity to deal with nonlinear data [8]. They are robust and overcome the problems like slow training rate, premature convergence faced in conventional neural networks. Initializing number of layers and weight is very critical task in designing a neural network. But these factors don’t play an important role in higher order neural network [4-10]. This network doesn’t use multiple layers and element in the input are drawn out with combinations of multiplied input.
In this work, the higher order neural network called Pi-Sigma neural network (PSNN) and functional link artificial neural network (FLANN) has been modeled using optimization method called glowworm swarm optimization algorithm [2,9]. The performance of the proposed method has been tested with various publicly available repositories. The remainder of this paper is organized as follows. Section 2 explains the basics about Pi-Sigma neural network (PSNN), Functional link artificial neural network (FLANN) and Glowworm Swarm optimization (GSO). In Section 3, the proposed work of PSNN and FLANN with GSO is explained. Experimental results have been explained in Section 4. Section 5 gives the conclusion and future works.
Methodology
Pi-Sigma neural network (PSNN)
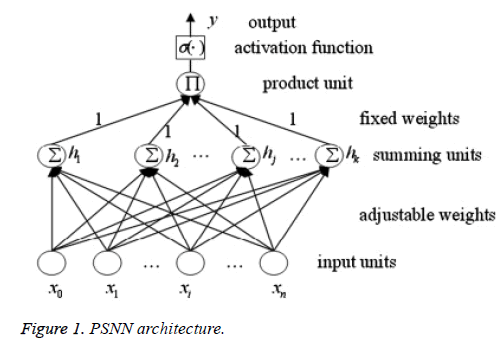
Higher order neural networks are successfully applied in many applications [3,10]. PSNN architecture is a higher order neural network developed by Shin and Ghosh [7]. It is a feed forward neural network with single hidden layer. The output layer has the product unit which calculates the summation and passes onto the activation function. This activation function should be able to handle nonlinear data. Shin and Ghosh defined PSNN as a neural network where polynomial of input variables is formed by a product (“pi”) of several weighted linear combinations (“sigma”) of input variables (Figure 1).
PSNN has good learning rates, low computational complexity and need less memory compared to other neural networks [10]. Also their accuracy is fairly good. The output of PSNN can be calculated as,
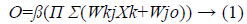
where β is the nonlinear activation function, Wkj and Wj are adjustable weights, Xk is the input data, N is the number of input, and K is the number of summation units which reflects the network order. When we add summing units network order increases by 1. Here the weights from summing layer to the output layer are fixed to unity. Hence learning rate and tunable weight values are greatly reduced. Summation units use linear function for more accurate training. Output layer utilizes sigmoid functions.
Functional link artificial neural network (FLANN)
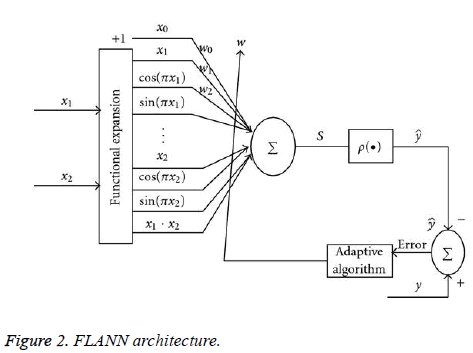
Artificial neural networks have been successfully used in variety of applications and it is an important tool in pattern recognition and nonlinear data processing. Traditional methods like Multilayer perceptron’s (MLP), radial basis functions (RBF) are widely used but the computational cost is very high. The presence of hidden layer increases the cost of computation in these methods. To reduce the computation cost FLANN [8] is proposed with no hidden layer. Since the hidden layer is removed the computational complexity is reduced and the speed of convergence is increased (Figure 2).
The initial step is to provide the inputs Xi where X is the number of input pattern and an error tolerance parameter ε. Next step is to randomly select the initial values of the weight vectors Wi, for, where “i” is the number of functional elements and Initialize Wi=Wi(0);For FLANN the functional block is made as follows:
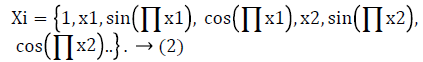
For functional based neural network models, the output was calculated as follows:

Output error is calculated as
Ei=oi-di → (4)
The weight matrixes are updated next using the following relationship:
Wi(k+1)=Wi(k)+S → (5)
where k is the time index and S is the momentum parameter.
Glowworm swarm optimization
GSO is a swarm intelligence optimization algorithm based on the behavior of glowworms [2]. It is based on the idea of glowworms changing intensity of luciferin emission and thus glows at different levels. In GSO a group of glowworms are distributed across search space. Luciferin is a luminescence quantity carried by the glowworms. Higher value of luciferin represents higher fitness value and better is its current location. A glowworm is attracted by its brightest neighbor within its domain. In each iteration, position of glowworms and their luciferin value changes [2]. GSO algorithm has two steps namely luciferin-update and movement phase. In luciferin – update phase the position of glowworms and value of the objective function at a time is taken into account. Here two constant values called luciferin decay constant and luciferin enhancement constant are set for calculating the luciferin value of a glowworm. That is, if position of glowworm at time t is xi(t), and its corresponding value of the objective function at glowworm i’s location at time t is J(xi(t)). The luciferin level associated with glowworm i at time is given by eq (6)
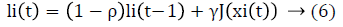
Where ρ is the luciferin decay constant (0<ρ<1), γ is the luciferin enhancement constant. The next step is to search for glowworm j closer to i using eq. (7)
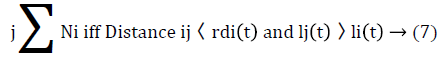
The probability of a Glowworm i moving towards a neighbor j is given by equation (8)
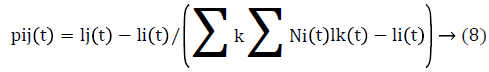
The position of glowworm i is updated using eq (9)
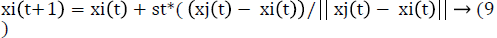
Where st is the step size. Then the range of neighborhood range is updated using eq (10).
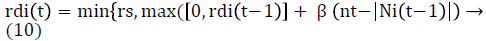
where β is a constant parameter and nt is a parameter used to control the number of neighbors . Glowworms move only in direction of line of sight of its neighbors.
Proposed Method
In the proposed approach, the FLANN and PSNN architecture is transformed into objective functions. The weight and bias values of the higher order neural network are fed into the GSO algorithm for finding the optimal weight parameters. The weights are tuned by the GSO algorithm based on error values. The weight set of PSNN and FLANN and the RMSE is calculated by training the network with the multimodal cancer dataset. Then the fitness of weight set w is computed from the sum of the root mean square error obtained from each instance of the dataset as 1/RMSE. The root mean square error (RMSE) is given as,
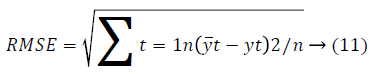
Where yt are the predicted values for n different predictions for t times. The error function can be calculated as,
Ej(t)=Oj(t)-Yj(t) → (12)
where Oj(t) represents the final desired output at time (t-1). At each time (t-1), the output of Yj(t) is calculated. The process continues until maximum number of iterations is reached or stopping criterion is reached.
Algorithm 1: FLANN/PSNN- GSO for Classification
Input: Cancer Dataset with target vector‘t’, initial population of weight-sets ‘P’, Bias B.
Output: PSNN / FLANN with optimized weight-set ‘w’.
Based on the GSO algorithm, each glowworm represents the solutions with a particular set of weight vector. The GSO algorithm [2] used for training the PSNN/FLNN is summarized as follow:
Step-1: Generate a random swarm of glowworms initially. X = {w1,w2,…wn}
Step-2: Compute the brightness of each glowworm by using objective function f(wi) as B = {B1,B2….Bn} = {f(w1),f(w2),… f(wn)}.
Step-3: Set luciferin decay constant 0 <ρ<1 and luciferin enhancement constant γ.
Step-4: While (t ≤ max iteration)
For i=1 to n
For j=1 to i
Calculate the luciferin value of the glowworms L using eq. (6).
If (Lj>Li)
Move glowworm i to j by using eq. (8).
End if
Position of the glowworm is updated using eq. (9)
Update the neighborhood range using eq. (10) and search for new solutions using eq. (7)
End for
End for
t = t+1.
End while
Step-5: Glowworms are ranked by their fitness and find the best one.
Step-6: If stopping criteria is reached, then go to step-7. Else go to step-4.
Step-7: Stop.
Algorithm 2: Weight Updation in PSNN/FLANN
1. FUNCTION F= Fitness From Training
2. FOR i = 1 to n, n is the length of the dataset (x, w, t, B)
3. Compute the output of the network by using eq. (1) and eq. (3).
4. Calculate the error term by using eq. (4) and compute the fitness F(i)=1/RMSE.
5. END FOR
6. Compute root mean square error (RMSE) by using eq. (11) from target value and output
7. The weight changes and updating of weight values by using the PSNN/FLANN-GSO algorithm can be computed by,
ΔWk= (ΠSj)xk where 1 ≤ j<n and Sj is the output of the summation layer.
8. IF the stopping criteria like training error or maximum no. of epochs are satisfied, then Stop.
ELSE repeat the step from 2 to 7.
9. END
Results
Experimental setup
The proposed technique is implemented using MATLAB on a system having the configuration of 256 G RAM and 2.8 GHz Intel i- 5 processor. A 256 GB RAM was preferred for doubling up the SSD storage which can be utilized if the proposed method is extended for online streaming based medical applications. Here a comparative analysis has been done between PSNN, PSNN-GSO with FLANN, FLANNGSO.
Data sources
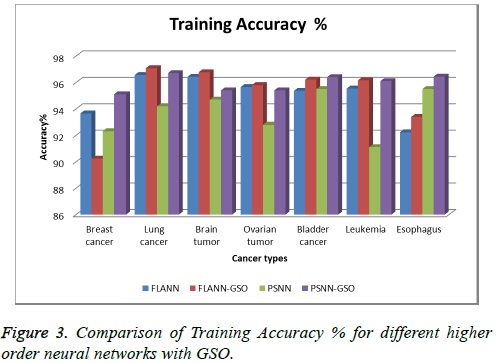
We tested our higher order neural network with glowworm swarm optimization technique on seven set of multimodal cancer data [5,9] like Breast cancer, Lung Cancer, Brain, Ovarian, and leukemia data sets. Breast cancer dataset contains cancer clump size, uniformity of cell size and shape, Marginal adhesion details of 700 patients. Lung cancer dataset contains survival time, age, sex; Karnofsky performance score rated by physician and patient, calories consumed and weight loss details of the patient. Brain tumor dataset contains contrast, correlation, homogeneity, shape index, skewness, and Kurtosis and tumor area dimension. Ovarian dataset contains observed time, censoring status, treatment group details, survival time and response time of about 200 patients. Leukemia dataset contains attributes like WBC count of nearly 30 patients. Esophageal cancer dataset contains details of patient’s age group, level of alcohol consumption, level of tobacco consumption for about 10 patients. Bladder dataset contains tumor size details of about 30 patients. These datasets are collected from publicly available domains like UCI machine repositories (Tables 1 and 2 and Figure 3).
| Datasets | Number of Instances | Number of Attributes |
Number of Classes |
|---|---|---|---|
| Breast cancer | 699 | 10 | 2 |
| Lung cancer | 32 | 56 | 2 |
| Brain tumor | 30 | 15 | 2 |
| Ovarian tumor | 27 | 6 | 2 |
| Bladder cancer | 32 | 2 | 2 |
| Leukemia | 34 | 3 | 2 |
| Esophagus | 89 | 5 | 2 |
Table 1. Dataset information.
| Datasets | Accuracy% FLANN |
Accuracy% FLANN-GSO |
Accuracy% PSNN |
Accuracy% PSNN-GSO |
||||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |
| Breast cancer | 93.652 | 93.004 | 90.231 | 91.547 | 92.31 | 93.02 | 95.1 | 94.6 |
| Lung cancer | 96.556 | 96.100 | 97.080 | 97.11 | 94.2 | 94.55 | 96.7 | 95.2 |
| Brain tumor | 96.422 | 96.410 | 96.77 | 96.211 | 94.7 | 94.77 | 95.4 | 95.43 |
| Ovarian tumor | 95.652 | 95.551 | 95.8 | 95.22 | 92.8 | 92.5 | 95.4 | 95.4 |
| Bladder cancer | 95.362 | 95.22 | 96.21 | 96.686 | 95.5 | 95.22 | 96.4 | 96.7 |
| Leukemia | 95.54 | 95.2 | 96.158 | 96.11 | 91.1 | 92.3 | 96.1 | 97 |
| Esophagus | 92.225 | 90.066 | 93.39 | 93.27 | 95.5 | 95.5 | 96.44 | 96.5 |
Table 2. Performance of high order neural network models in terms of training and testing Accuracy for multimodal Cancer datasets.
Comparison of performance of FLANN with FLANN-GSO shows increase in accuracy values in FLANN-GSO for most of the tumor datasets. Accuracy of PSNN-GSO also shows increase in values than PSNN.
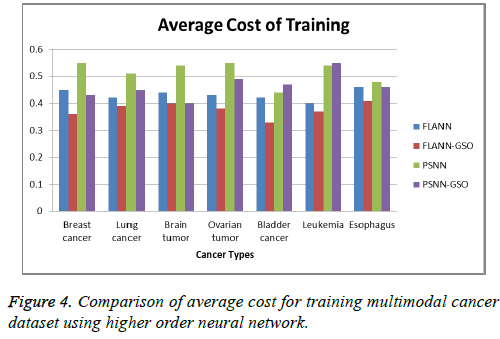
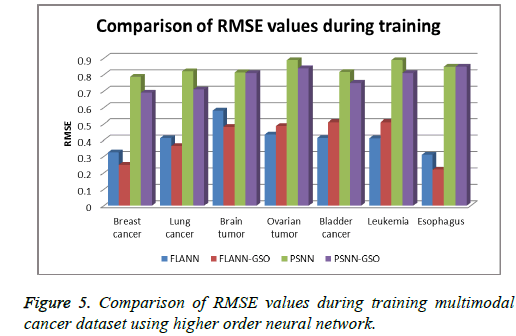
Comparison of computational cost for both PSNN and FLANN with and without GSO is done. Results show a decrease in cost values when classification in higher order networks is done with optimization techniques (Tables 3 and 4 and Figures 4 and 5).
| Datasets | FLANN | FLANN-GSO | PSNN | PSNN-GSO | ||||
|---|---|---|---|---|---|---|---|---|
| Ctrain | Ctest | Ctrain | Ctest | Ctrain | Ctest | Ctrain | Ctest | |
| Breast cancer | 0.45 | 0.41 | 0.36 | 0.33 | 0.55 | 0.52 | 0.43 | 0.44 |
| Lung cancer | 0.42 | 0.41 | 0.39 | 0.39 | 0.51 | 0.51 | 0.45 | 0.44 |
| Brain tumor | 0.44 | 0.4 | 0.4 | 0.4 | 0.54 | 0.51 | 0.4 | 0.4 |
| Ovarian tumor | 0.43 | 0.43 | 0.38 | 0.38 | 0.55 | 0.54 | 0.49 | 0.44 |
| Bladder cancer | 0.42 | 0.41 | 0.33 | 0.33 | 0.44 | 0.41 | 0.47 | 0.44 |
| Leukemia | 0.4 | 0.4 | 0.37 | 0.33 | 0.54 | 0.55 | 0.55 | 0.55 |
| Esophagus | 0.46 | 0.44 | 0.41 | 0.4 | 0.48 | 0.45 | 0.46 | 0.41 |
Table 3. Average cost for training and testing cancer data sets.
Conclusion
In this paper, a bio inspired glowworm swarm optimization algorithm based higher order neural network is proposed for classification of multimodal cancer data. Higher order neural network based methods are used to classify multimodal tumor datasets. Results show that the FLANN-GSO and PSNN-GSO methods provide better accuracy than basic PSNN and FLANN. For future enhancements, other higher order neural networks can be tested with GSO or other swarm intelligence based optimization algorithms for better accuracy.
References
- Al-Jumeily D, Ghazali R, Hussain A. Predicting physical time series using dynamic ridge polynomial neural networks. PLoS ONE 2014; 9: e105766.
- Karegowda AG, Prasad M. A survey of applications of glowworm swarm optimization algorithm. Int J Comput Appl 2013.
- Nayak J, Naik B, Behera HS. A novel nature inspired firefly algorithm with higher order neural network: Performance analysis. Int J Eng Sci Technol 2016; 19: 197-221.
- Fallahnezhad M, Moradi MH, Zaferanlouei S. A hybrid higher order neural classifier for handling classification problems. Exp Syst Appl 2011; 38: 386-393.
- Liang M, Li Z, Chen T, Zeng J. Integrative data analysis of multi-modal cancer data with a multimodal deep learning approach. EEE Transact Comput Biol Bioinformat 2015.
- Ghazali R, Hussain AJ, Liatsis P. Dynamic ridge polynomial neural network: forecasting the univariate non-stationary and stationary trading signals. Exp Syst Appl 2011; 38: 3765-3776.
- Ghazali R, Husaini NA, Ismail LH, Samsuddin NA. an application of jordan pi-sigma neural network for the prediction of temperature time series signal. In: Ubiquitous computing and multimedia applications. Springer, Berlin, 2011.
- Nanda SK, Tripathy DP. Application of functional link artificial neural network for prediction of machinery noise in open cast mines. Corporat Adv Fuzzy Syst 2011.
- Agrawal S, Agrawal J. Neural network techniques for cancer prediction: A survey. Procedia Comput Sci 2015; 60: 769-774.
- Shin Y, Ghosh J. Ridge polynomial networks. IEEE Trans Neural Networks 1995; 6: 610-622.