Research Article - Biomedical Research (2017) Volume 28, Issue 5
Combination of fuzzy c-means clustering and texture pattern matrix for brain MRI segmentation
Shijin Kumar PS1*, Dharun VS21Department of Electronics and Communication Engineering, Noorul Islam University, Kumaracoil, Tamil Nadu, India
2Archana College of Engineering, Palamel, Nooranad, Alappuzha, Kerala, India
- *Corresponding Author:
- Shijin Kumar PS
Department of Electronics and Communication Engineering
Noorul Islam University
Tamil Nadu, India.
Accepted date: September 23, 2016
Abstract
The process of image segmentation can be defined as splitting an image into different regions. It is an important step in medical image analysis. We introduce a hybrid tumor tracking and segmentation algorithm for Magnetic Resonance Images (MRI). This method is based on Fuzzy C-means clustering algorithm (FCM) and Texture Pattern Matrix (TPM). The key idea is to use texture features along with intensity while performing segmentation. The performance parameters can be improved by using Texture Pattern Matrix (TPM). FCM is capable of predicting tumor cells with high accuracy. In FCM homogeneous regions in an image are obtained based on intensity. Texture Pattern Matrix (TPM) provides details about spatial distribution of pixels in an image. Experimental results obtained by applying proposed segmentation method for tracking tumors are presented. Various performance parameters are evaluated by comparing the outputs of proposed method and Fuzzy C-means algorithm. The computational complexity and computation time can be reduced by using this hybrid segmentation method.
Introduction
The quality of a Magnetic Resonance Images (MRI) reduces due to inhomogeneity of intensity distribution, partial volume (PV) effect and noise. It is possible to overcome these impediments by using soft segmentation methods such as Fuzzy C-means (FCM) clustering algorithm. FCM algorithm was introduced by Dunn [1] in the year 1974. In FCM the vector space is subdivided into number of subspaces based on the distance vector [2]. The performance of FCM can be further improved by considering the texture of the MR image. A novel method for Texture Quantization (TQ) is proposed and the Texture characteristics are incorporated with FCM. The accuracy and efficiency of segmentation can be improved by using Texture Quantization.
Rajesh et al. proposed a robust and improved FCM clustering algorithm [3]. Advantage of this method is the non dependence of algorithm with distance measures. The performance parameters are generalized. The accuracy of this method is high compared with conventional FCM. John F. et al. proposed a real time FCM for fast segmentation [4]. The number of update equations is reduced to one. Thus the time consumption is very much reduced. The major advantage is the requirement of lower memory. Anand Gaonkar et al. [5] introduced a modified Fuzzy c-means algorithm to reduce noise sensitivity. The intensity of spatial neighbourhood pixels is incorporated with standard FCM clustering. The membership weights of each cluster are modified for this purpose. Szilagyi et al. proposed a modified FCM clustering method to reduce sensitivity [6]. The scalar feature values are extracted from adjacent pixels. The method deals with both spatial distance and gray level distance. Wang et al. proposed a modified FCM using local and global information of pixels [3]. Use of distance vector is avoided in this method. Instead of distance vector, dissimilarity index is used. The major flaw of this method is the increment in computational complexity [3].
This paper proposes a complexity reduced brain MRI segmentation algorithm using FCM and Texture Quantization. A comprehensive discussion on proposed methodology is given in upcoming sections. The experimental results obtained by applying the proposed algorithm are demonstrated and the performance of proposed algorithm is compared with the performance of FCM clustering algorithm.
Materials and Methods
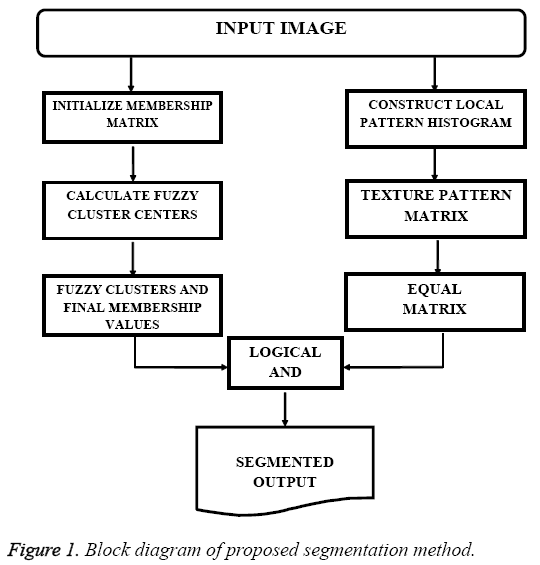
The input images required for the experiment were obtained from Cancer Image Archive [8]. In order to obtain better computational speed, the size of MR images are reduced to 256x256. The proposed algorithm is implemented using MATLAB. Initially the input images are pre-processed to obtain better efficiency. The pre-processing steps involved are image enhancement and skull stripping. Image enhancement is done using contrast limited adaptive histogram equalization (CLAHE) [9,10]. Skull stripping is based on Morphological Operation and Connected Regions [9]. The proposed method is a combination of Fuzzy C-means (FCM) clustering algorithm and Texture Pattern Matrix (TPM). FCM allocates data points in an image to various clusters and assigns membership values to each data points in a cluster. The membership value denotes the association of a particular data point with the cluster. Texture provides information on spatial organisation of colors and intensities in the image or a particular region of the image. The elements of Texture Pattern Matrix (TPM) are obtained by comparing each pixel with neighbouring pixels. Block diagram presented in Figure 1 describes the proposed novel segmentation method.
Fuzzy C-means (FCM) allocates data inside multiple clusters and assign different membership values. Initial fuzzy partition matrix is developed and the initial fuzzy clusters are calculated. Membership value is assigned to each pixel. The objective function is converged to find the optimum position of pixels in clusters. Iteration of FCM is done over two parameters: membership value and cluster center. Iteration process stops when optimum values are obtained. FCM divides the dataset consisting of n vectors into C groups. A cluster center is calculated from each group. The data point can belong to several groups, with a degree of association. The association of the pixels with data groups is denoted as membership values. The membership values lies between the range 0 and 1. The initialization of the membership matrix (M) can be done using any random values between the range 0 and 1. Center of C fuzzy clusters are calculated using the equation,
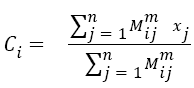 →(1)
→(1)
Where i=1, 2, 3, ..... c. The cost is calculated from M and Ci. If the cost is below a threshold value, the computation stops. If the cost obtained is minimum compared to the cost from previous iteration, then the computation stops. The cost is calculated from the equation,
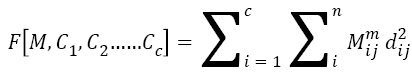 →(2)
→(2)
Compute new M using the equation,
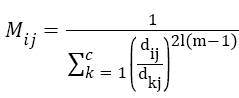 →(3)
→(3)
The new M obtained from equation (3) is applied to equation (1). This iteration process discontinues, if the difference between objective functions obtained from two successive iterations is less than a threshold value.
Local Pattern Histogram (LPH) is a tool used to estimate the local behavior of pixel intensities in an image. Here a moving window is used to compare neighboring pixels with center pixel. Quantization and Matrix Splitting are the major steps involved in the calculation of LPH. Quantization process is done using a moving window (here the size of moving window is taken as 5x5). The intensity of central pixel is compared with the intensities of each and every pixel inside the window. Mathematically, quantization procedure can be expressed as an indicator function and is given by,
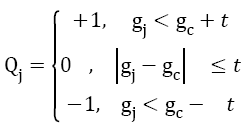 →(4)
→(4)
where, gc is the intensity of the central pixel, gj is the intensity of pixel j in the local window. Using trial and error method the threshold value t is taken as 4. Then 0 is assigned to all the pixels having intensities in the range gc ± t. +1is assigned to all the pixels having intensities above this range. All other pixels are replaced with -1. The image thus obtained from the quantization process is referred to as Texture Pattern Matrix (TPM). This matrix represents the texture characteristics of the input image.
In Matrix Splitting, the Texture Pattern Matrix (TPM) is again divided into three new matrices. First one is Positive Matrix (PM), which highlights pixels with positive values. Equal Matrix (EM) emphasizes pixels with 0 intensity value. Negative Matrix (NM) highlights pixels with negative intensity values. These matrices and TPM have the same size. Positive Matrix (PM) is derived by altering the value of pixels in TPM. Pixels with positive intensity value (greater than zero) are replaced with 1 and all other pixels are replaced with 0.
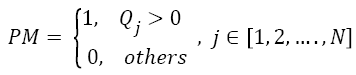 →(5)
→(5)
To calculate Equal Matrix (EM), Pixels with intensity value equal to zero are replaced with 1 and all other pixels are replaced with 0.
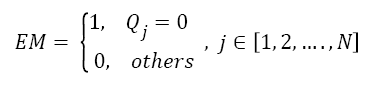 →(6)
→(6)
To calculate Negative Matrix (NM), pixels with intensity value less than zero are substituted with 1 and rest of the pixel intensities are substituted with 0. This can be mathematically formulated as an indicator function.
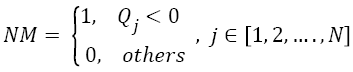 →(7)
→(7)
Pixels having similarity in texture features are grouped to form Equal Matrix (EM). EM refers to the tumor structure and it can be used for further calculations. The Fuzzy C-means segmented output is AND operated with the EM output to get the final segments. The output thus obtained exhibits texture correlation, along with the segmented regions.
Experimental Results
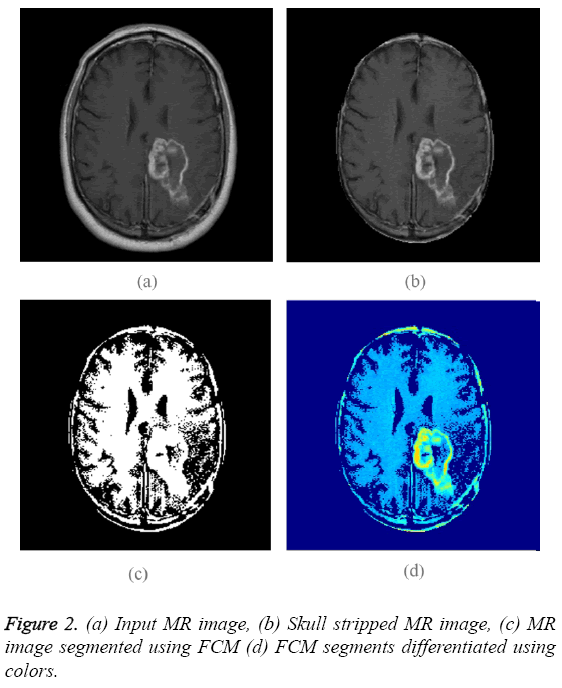
T-1 weighted MR images of size 256 × 256 are used for experimentation purpose. The input image is shown in Figure 2a. Initially skull region is removed from the given MR image using a skull stripping algorithm based on connected regions and morphological operation [9]. Application of skull stripping algorithm can increase the efficiency of segmentation. It also reduces false detection of tumor region. Figure 2b displays skull stripped brain MR image which contains region of interest. Fuzzy C-means (FCM) alone is applied on skull stripped image.
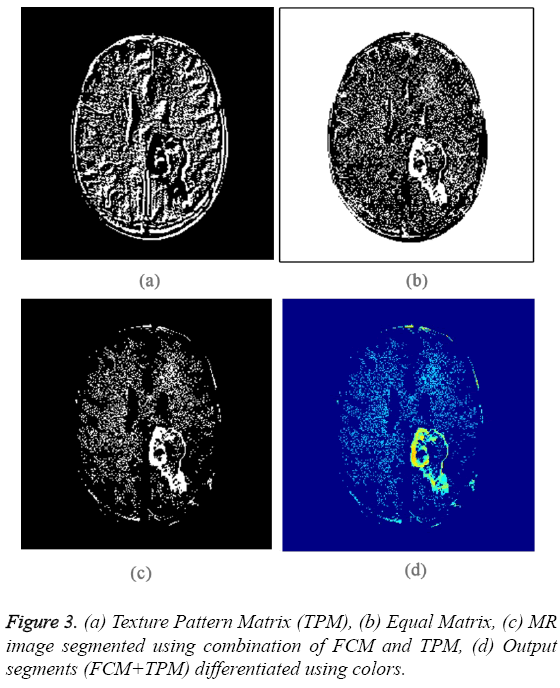
The obtained binary segments are shown in Figure 2c. This segmented output image is used for evaluating the performance of proposed segmentation method. Each segment is indicated using a particular color and the colored segments are shown in Figure 2d. The input image is converted into Texture Pattern Matrix (TPM), which reflects the texture characteristics of all regions. The output of TPM is shown in Figure 3a. The texture characteristics of tumor region have to be found out. Tumor regions exhibit unique texture properties and these regions can be identified using Equal matrix (EM). Equal Matrix (EM), which contains regions with similar texture characteristics, is shown in Figure 3b. Final segmented output is obtained by fusing the FCM binary segments and Equal Matrix (EM). The FCM segmented binary output is AND operated with Equal Matrix (EM). The final segmented binary output obtained using the combination of FCM clustering segmentation and Texture Pattern Matrix is shown in Figure 3c. Figure 3d indicates the colored output segments. By comparing Figure 2d and Figure 3d is clear that the segmented output obtained using proposed method is better than FCM segmented output.
Discussion
The comparison results between Fuzzy C-means segmentation and proposed method (FCM+TPM) is shown in Table 1. Each output is compared with manual reference for accuracy. There is a huge increase in accuracy of segmentation when compared with the traditional FCM segmentation method. Peak signal to noise ratio is increased by 6. Mean square error is reduced by 18%. Correlation, Dice Coefficient and Specificity have also increased significantly by using proposed methodology.
| Parameters | FCM | FCM + TPM |
|---|---|---|
| PSNR | 54.3077 | 60.2913 |
| Mean Square Error | 0.2412 | 0.0608 |
| Correlation | 0.1843 | 0.2722 |
| Dice Coefficient | 0.0905 | 0.2132 |
| Specificity | 75.6141 | 94.2546 |
| Accuracy | 75.88 | 93.92 |
Table 1: Performance of Proposed Method in Comparison with FCM Segmentation.
Conclusion
In this paper FCM algorithm is combined with Texture Pattern Matrix to segment region of interest (ROI). The proposed brain MRI segmentation method is robust and computational complexity is less. The algorithm uses simple statistical technique to develop a novel segmentation method. The proposed method makes use of texture analysis to improve the efficiency of brain tumor segmentation. This method is compared with FCM and manual reference to verify accuracy and other parameters. Our method shows higher value of PSNR, Dice Coefficient, Correlation, Specificity and Accuracy. MSE is very much low compared to FCM.
References
- Joseph DC. Well-separated clusters and optimal fuzzy partitions. J Cybernetics 1974; 4: 95-104.
- James BC, Hall LO, Clarke LP. Review of MR image segmentation techniques using pattern recognition. Med Physics 1992; 20: 1033-1048.
- Dave RN, Sen S. Robust fuzzy clustering of relational data. IEEE Transact Fuzzy Syst 2002; 10: 713-727.
- John KF, Hutcheson T. Reducing the time complexity of the fuzzy c-means algorithm. IEEE Transact Fuzzy Syst 2002; 10: 263-267.
- Anandgaonkar GP, Sable GS. Detection and Identification of Brain Tumor in Brain MR Images Using Fuzzy C-Means Segmentation. Int J Adv Res Comput Commun Eng IJARCCE 2013; 2: 3964-3967.
- Szil´agyi L, Szil´agyi SM, Beny´o Z. A modified fuzzy c-means algorithm for mr brain image segmentation, in Image Analysis and Recognition. Springer, 2007, pp. 866-877.
- Kumar SP S, Dharun VS. A Study of MRI Segmentation Methods in Automatic Brain Tumor Detection. Int J Eng Technol 2016; 8: 609-614.
- www.cancerimagingarchive.net
- Kumar SP S, Dharun VS. An efficient skull stripping algorithm using connected regions and morphological operation. ARPN J Eng Appl Sci 2016; 11: 4305-4309.
- Reza AM. Realization of the contrast limited adaptive histogram equalization (CLAHE) for real-time image enhancement. J VLSI Signal Process Syst Signal Image Video Technol 2004; 38: 35-44.