Research Article - Biomedical Research (2018) Volume 29, Issue 10
Application of TAR signature for breast mass analysis
Spandana Paramkusham1*, Kunda MM Rao2, Prabhakar Rao BVVSN2 and Shivam Sharma2
1Bits, Pilani-Hyderabad Campus, Jawahar Nagar, Shameerpet Mandal, R.R. District, Hyderabad, India
2Department of Electrical Engineering, Bits, Pilani-Hyderabad Campus, Jawahar Nagar, Shameerpet Mandal, R.R. District, Hyderabad, India
Accepted date: March 13, 2018
DOI: 10.4066/biomedicalresearch.29-17-260
Visit for more related articles at Biomedical ResearchAbstract
Breast cancer is the most common cancer among women. Our paper mainly focuses on classification of breast masses with the Triangular Area Representation (TAR) signatures. Breast masses are characterized by its gray level values and shape complexity. So, shape descriptors are calculated from the TAR signature of mass contours and given to different classifiers for the classification of benign and malignant contours .We tested our proposed method on 148 mass contours which are taken from DDSM mammogram database. Out of the total images used for evaluation 74 images were malignant and other 74 images were benign. The proposed method attained accuracy of 90.9% and 0.95 AUC (Area Under Curve) value with SVM (support vector machine) classifier
Keywords
Mammograms, Breast masses, Contours, TAR, SVM classifier
Introduction
Breast cancer is the second most common cancer worldwide. About 25% to 32% of all female cancers are breast cancers in India [1]. Mammography is one of the most widely used imaging modality for screening breast cancer. Masses are the most common abnormality present in breast cancer patients and they are formed when healthy cells grow abnormally at one place. Masses can be characterized by various descriptors like shape, size and margins. They can be classified into benign and malignant masses. Benign (non-cancerous) masses usually have oval, lobulated, and round shapes with smooth circumscribed margins. Malignant (cancerous) masses have irregular, ill-defined and microlobulated shapes with spiculated margins.
Literature Survey
We can classify breast masses based on shape characteristics. The mass is differentiated by its gray scale, margin and its shape characteristics. Many texture based methods were introduced to classify masses as benign and malignant. Gabor transforms, spherical wavelet transforms, contourlet transforms, wavelet transforms, ripplet transforms local energy based descriptors, and fractal dimensions are some proposed texture methods in the literature for classification of breast masses [2-8]. These texture methods generates high dimensional feature vector which increases the computational complexity of CAD (Computer Aided Diagnosis) system. In order to decrease the length of feature vector many methods have been introduced for classifying breast masses using 2D contour or shape characteristics of masses. In [9] Rangayan et al. calculated Spiculation Index (SI) and fractional concavity (fcc) on 2D mass contours. Rojas et al. [10] proposed two shape features of mass contours. One measures the degree of spiculation of a mass and other measures its likelihood of being spiculated. Mencattini et al. [11] applied fuzzy c-means algorithm for segmentation of contours from mammogram. Fractal analysis methods were proposed for extraction of features. They classified the contours into benign/malignant using SVM, KNN and Bayes classifier. Khaligh et al. [12] extracted margin features of masses using wavelet transforms without any prior segmentation.
Very few studies have proposed the methods for classifying breast masses based on 1D shape characteristics of mass contours. In these methods the 2D contours are converted into 1D signals to reduce the computational complexity. Among them Rangayan et al. [13] applied fractal analysis on the 1D signature of mass contours and attained accuracy of 80%. Rangayan et al. calculated fractal dimension using power spectrum from 1D signatures to classify benign/malignant masses [14]. Ten 1D signals were generated from radial and circular scan lines [15]. These 1D signals were analysed using wavelet transform to classify masses. Texture, shape and margin features have been extracted from mass ROIs to classify them [16]. In this paper shape features are extracted by converting mass ROI into 1D signals. The aim of the present study is to extract shape complexity feature from TAR signature for the classification of breast masses. Only a few studies have proposed on 1D shape characteristics of mass contours. Benign and malignant tumors differ by their shape complexity therefore, feature descriptor derived from the TAR signatures of mass contours help in delineating masses into benign and malignant.
Materials
In this paper we have used mass contours as dataset for evaluation. Mass contours are extracted from mammograms based on radiologist’s information and they are obtained from DDSM database. The DDSM images [17] are taken from Massachusetts General Hospital, Washington University School of Medicine, Wake. They have 2620 cases in 43 volumes. In this study we have used 148 mass contours. Among these mass contours, 74 were benign and other 74 were malignant cases.
Methods
The proposed method starts with manual extraction of mass contours from DDSM database. These contours were drawn by radiologists. Figures 1a and 1b show benign and malignant contours. Then the 2D contours are converted into 1D TAR signatures for feature extraction process. The feature descriptors extracted from signatures are submitted to SVM classifier for further analysis of mass. The flowchart in Figure 2 explains the stages of the proposed method.
Conversion of 2D contour into 1D signal
Triangular area representation (TAR) signatures: We have applied triangular area function to study the complexity of mass contours. TAR converts 2D contour into 1D signal. It uses all boundary points in mass contour to measure the convexity/concavity of each point at different scales [18]. This 1D TAR signature is invariant to translation, rotation, and scaling. TAR signature is computed by area formed by three consecutive points on boundary. Consider 2D closed mass boundary having N boundary points with x and y coordinates.
Let three consecutive points on mass contour be (xn-ts, yn-ts), (xn, yn), and (xn+ts, yn+ts), where n (1, N) and ts (1, Ts) is the triangle side. The signed area of the triangle formed by these points is given below in Equation 1.
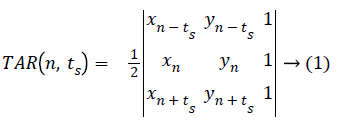
ts=1,2,3,4.......Ts, where the maximum Ts depends on periodicity of N.
When we traverse the contour in counter clock wise direction positive, negative and zero values of TAR signature represents convex, concave and straight line points on contour.
The triangle side length value (ts) depends on the value of number of points (N) on contour. Equation 2 gives values of TAR with respect to N.
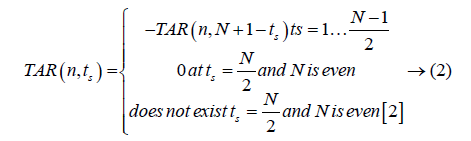
Feature extraction from TAR signature: As TAR signature gives number of concave and convex points. The ratio of number of concave points to number of convex points (R) is taken as a feature descriptor for different values of ts and it is given below in Equation 3.
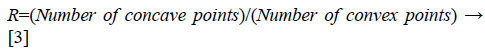
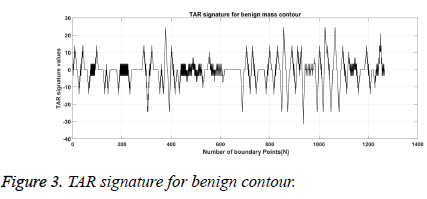
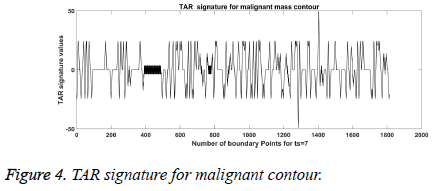
From Figures 1a and 1b we can observe that malignant mass contour is very complex and benign contours smooth. Figures 3 and 4 show TAR signatures of malignant and benign mass contours. From the TAR signatures we can observe that they are many convex and concave regions in malignant TAR signature and many straight lines in benign TAR signature.
From the value of R we can discriminate mass contour or boundaries. To give more discrimination power to feature descriptors we calculated area, perimeter and eccentricity to mass contours. These feature descriptors are submitted to classifier for further validation.
Classification
SVM classifier: SVM classifier is used in this paper to classify the mass contours into two classes i.e. benign and malignant. It is a supervised machine learning rule which constructs the optimal hyper planes in high dimensional feature space. These two planes maximize the margin of separation between feature vectors of two classes. The maximal margin (distance between two hyperplanes) is determined with the help of support vectors (training data) [19].
The two classes that we are using are malignant and benign. For two class classification, yi be (+1,-1) be a label matrix and X be a training samples. Then N labeled training samples is represented by: (y1, x1),..............(yN, xN) where yi (-1,+1) represents class label and xi (i=1,2...N) represents dataset.
The generalized equation for linearly separable data that maximizes the margin is given in Equation 4.
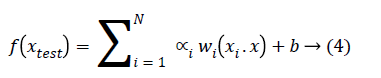
Where w is weight vector and b is a scalar and xtest is a new object that has to be classified.
The generalized equation for non-seperable data is given in Equation 5.
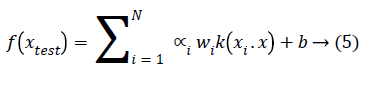
Where kernel function k (xi.x) can be linear, quadratic, Gaussian etc.
Results
Dataset
The dataset used for analysis consists of 148 mass contour images taken from DDSM database. For evaluation we have used hold out methodology. We have tested our proposed TAR descriptor with different configurations of testing vs. training images. The simulations have been carried out using MATLAB 2015a. The personal computer has an Intel Core i7-6500U processor and 8 GB Random Access Memory (RAM).
Assessment parameters
The performance of our method is measured in terms of sensitivity, specificity, accuracy and AUC (Area under the ROC (Receiver Operating Characteristics) curve). These terms are explained below.
Sensitivity (Sens)=TP/((TP+FN))
Specificity (Spec)=TN/((TN+FP))
Accuracy (Acc)=(TP+TN)/( TP+TN+FP+FN)
Where, TP, FP, TN, FN are true positive, false positive, true negative and false negative respectively.
Sensitivity measures the percentage of malignant cases that are correctly classified. Specificity is the percentage of benign cases that are correctly classified. AUC and accuracy specifies overall CAD system performance.
TP: Number of malignant cases detected correctly.
TN: Number of benign cases detected correctly.
FN: Number of malignant cases detected as benign.
FP: Number of benign cases detected as malignant.
We extracted feature descriptors using five cases, those are ts=1 to 3, ts=1 to 5, ts=1 to 7, ts=1 to 10 and ts= 1 to 20. R values are taken as features for all five cases. Along with this we added geometric parameters like area, perimeter and eccentricity values to add more discriminative power to feature descriptor. These feature descriptors are given to classifiers for further validation. The length of feature descriptors which attained best accuracy of 90.9% (for ts=1 to7) for each mass contour is ten. It includes seven R values for each value of ts, area, perimeter and eccentricity of mass contour.
Table 1 gives the output accuracies of all five different classifiers and five different cases of feature descriptors (based on ts values). The classifiers that we tested with our feature descriptors are SVM (linear kernel), SVM (quadratic kernel), Simple tree, weighted KNN and ensemble adaboost classifiers. These classifiers are modeled with 15% (22) of testing cases and 85% (126) training cases. Table 1 indicates supremacy of SVM (quadratic classifier) as it has given highest accuracy of 90.9%.
| Classifiers | ts=1 to 3 | ts=1 to 5 | ts=1 to 7 | ts=1 to 10 | ts=1 to 20 |
|---|---|---|---|---|---|
| SVM (linear) | 54.5 | 72.7 | 86.4 | 54.5 | 63.6 |
| SVM (Quadratic) | 54.5 | 72.7 | 90.9 | 54.5 | 50 |
| Simple tree | 63.6 | 63.6 | 81.8 | 59.1 | 72.7 |
| Weighted KNN | 72.7 | 59.1 | 81.8 | 63.6 | 63.6 |
| Ensemble Adaboost | 59.1 | 63.6 | 81.8 | 59.1 | 77.3 |
Table 1: Accuracies in % with different classifiers.
We also considered different ratios of testing/training mass contour images in Table 2 with feature descriptor obtained from ts=1 to 7. The distribution of 148 mass contours for training and testing of the SVM model was performed in four different ways: first, we used 15% for testing and 85% for training (composed of 148 mass contours with 22 testing images and 126 training images) and obtained accuracy of 90.9% with SVM (quadratic kernel). Second, we used 30% for testing and 70% for training (composed of 148 mass contours with 45 testing images and 103 training images) and obtained accuracy of 82.2% with SVM (quadratic kernel). Third, we used 50% for testing and 50% for training (composed of 148 mass contours with 74 testing images and 74 training images) and obtained accuracy of 82.4% with SVM (quadratic kernel) and finally we used 40% for testing and 60% for training (composed of 148 mass contours with 59 testing images and 89 training images) and achieved accuracy of 83.1% with SVM (quadratic kernel) as shown in Table 2. Therefore, from Table 2, we can conclude that the accuracies obtained with different number of testing images is above 80%.
| Testing/training: (No. of images used for testing)/(No of images for training) | Acc (%) | Classifier | TN | TN | FP | FN |
|---|---|---|---|---|---|---|
| 15/85: (22)/(126) | 90.9 | SVM (quadratic) | 10 | 10 | 1 | 1 |
| 30/70: (45)/(103) | 82.2 | SVM (quadratic) | 19 | 18 | 3 | 5 |
| 50/50: (74)/(74) | 82.4 | SVM (quadratic) | 26 | 35 | 11 | 2 |
| 40/60: (59)/(89) | 83.1 | SVM (quadratic) | 21 | 28 | 8 | 2 |
Table 2: Results achieved with different testing/training configuration using for 148 mass contours.
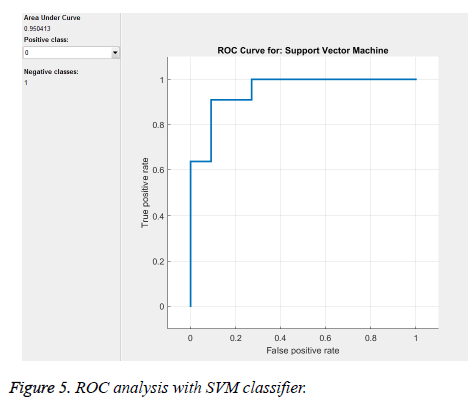
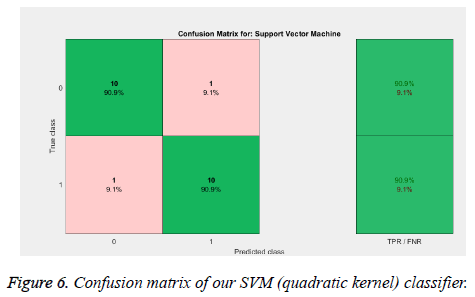
From the above Tables 1 and 2, and Figure 5 we can infer that our proposed method gave best accuracy of 90.1% using SVM (quadratic kernel) classifier and AUC value of 0.950413 with 15% of testing images (22) and 85% of training images (126). Figure 6 gives confusion matrix i.e., TN, TP FP and FN’s with our classifier. This figure shows that we obtained sensitivity of 90.9% and specificity of 90.9% with SVM classifier. We also compared our method with conventional methods in Table 3. Thus, it proves that the obtained results show that our method attained good accuracy with only ten features. We extracted feature vector from TAR signatures and given to SVM for classification to classify mass contours into benign/malignant.
| Feature extraction method | Images | Acc (%) | Sens (%) | Spec (%) | AUC |
|---|---|---|---|---|---|
| GaborPCA [2] | 114 | 80 | - | - | - |
| Fractional concavity and spiculation index [9] | 111 | 82 | - | - | 0.79 |
| Fractal dimension using ruler method and fractional concavity [11] | 111 | - | - | - | 0.82 |
| Margin Features [12] | 100 | 85.7 | - | - | - |
| Wavelet analysis on 1D signals [15] | 57 | 85.96 | - | - | - |
| Ripplet transform and GLCM [7] | 200 | - | - | - | 0.83 |
| Texture, shape and margin features [16] | 192 | 88.02 | - | - | - |
| Proposed method | 148 | 90.9 | 90.9 | 90.9 | 0.95 |
Table 3: Comparison of accuracies, specificity, sensitivity and AUC with our proposed method.
Conclusion
In this paper we have presented the application of TAR signatures for the classification of malignant and benign mass contours in mammogram. The feature descriptors calculated from TAR signature gives information on number of concave and convex points in the contour. Thus, the obtained values for accuracy, sensitivity and specificity are high compared to other state of art methods as shown in Table 3. The proposed method attained accuracy of 90.9%, sensitivity of 90.9%, and specificity of 90.9% and AUC value of 0.95 by considering 15% of testing images and 85% of training images. From these results we can conclude that our method gave satisfying results for the classification of masses into benign and malignant. Additional advantage of our method is, it takes less computation time as the number of features is only ten when compared many multi-resolution methods. Our future work includes the classification of breast masses based on BIRADS lexicon with various shape based features.
References
- Sengupta D, Bandyopadhyay S. Topological patterns in microRNA-gene regulatory network: studies in colorectal and breast cancer. Mol Biosyst 2013; 9: 1360-1371.
- Buciu I, Alexandru G. Directional features for automatic tumor classification of mammogram images. Biomed Sig Proc Control 2011; 6: 370-378.
- Gorgel P, Ahmet S, Osman NU. Mammographical mass detection and classification using local seed region growing-spherical wavelet transform (lsrg-swt) hybrid scheme. Comp Biol Med 2013; 43: 765-774.
- Moayedi F, Zohreh A, Reza B, Serajodin K. Contourlet-based mammography mass classification using the SVM family. Comp Biol Med 2010; 40: 373-383.
- Do Nascimento MZ, Martins AS, Neves LA, Ramos RP, Flores EL, Carrijo GA. Classification of masses in mammographic image using wavelet domain features and polynomial classifier. Exp Sys Appl 2013; 40: 6213-6221.
- Wajid SK, Hussain A. Local energy-based shape histogram feature extraction technique for breast cancer diagnosis. Exp Sys Appl 2015; 42: 6990-6999.
- Rabidas R, Chakraborty J, Midya A. Analysis of 2D singularities for mammographic mass classification. IET Comp Vis 2016.
- Beheshti SM, Noubari HA, Fatemizadeh E, Khalili M. Classification of abnormalities in mammograms by new asymmetric fractal features. Biocybern Biomed Eng 2016; 36: 56-65.
- Rangayyan RM, Naga RM, EL Desautels J. Boundary modelling and shape analysis methods for classification of mammographic masses. Med Biol Eng Comp 2000; 38: 487-496.
- Do Nascimento MZ, Martins AS, Neves LA, Ramos RP, Flores EL, Carrijo GA. Classification of masses in mammographic image using wavelet domain features and polynomial classifier. Exp Sys Appl 2013; 40: 6213-6221.
- Mencattini A, Salmeri M, Casti P, Raguso G, LAbbate S, Chieppa L, Ancona A, Mangieri F, Pepe ML. Automatic breast masses boundary extraction in digital mammography using spatial fuzzy c-means clustering and active contour models. InMedical Measurements and Applications Proceedings (MeMeA) IEEE International Workshop 2011; 632-637.
- Bagheri-Khaligh A, Ali Z, Manzuri-Shalmani MT. Novel margin features for mammographic mass classification. Mac Learn Appl 2012; 2: 139-144.
- Rangayyan RM, Nguyen TM. Fractal analysis of contours of breast masses in mammograms. J Digit Imaging 2007; 20: 223-237.
- Rangayyan RM, Oloumi F, Nguyen TM. Fractal analysis of contours of breast masses in mammograms via the power spectra of their signatures. Engineering in Medicine and Biology Society (EMBC), 2010 Annual International Conference of the IEEE 2010; 6737-6740.
- Dash JK, Laxmikant S. Wavelet based features of circular scan lines for mammographic mass classification. Rec Adv Info Technol 2012; 58-61.
- Chokri F, Merouani HF. Mammographic mass classification according to Bi-RADS lexicon. IET Comp Vis 2016.
- Benndorf M, Herda C, Langer M, Kotter E. Provision of the DDSM mammography metadata in an accessible format. Med Phys 2014; 41: 051902.
- Alajlan N, El Rube I, Kamel MS, Freeman G. Shape retrieval using triangle-area representation and dynamic space warping. Patt Recogn 2007; 40: 1911-1920.
- Cortes C, Vladimir V. Support-vector networks. Mac Learn 1995; 20: 273-297.