Research Article - Biomedical Research (2017) Artificial Intelligent Techniques for Bio Medical Signal Processing: Edition-I

Application of labelled digraphs in protein networks for medical technology

Sathyabama University, India

*Corresponding Author:

Rajeswari R
Sathyabama University, India

Accepted on March 10, 2017

Abstract

In this paper we prove the edge graceful labeling methods on regular digraphs and characterized the same for regular digraphs. We also discuss the importance of labeled digraphs in biological networks. A digraph is said to be regular directed graph, if it satisfies the stronger condition that the indegree and outdegree of each vertex are equal to each other and same for every vertex.

Keywords

Edge graceful, Strong edge graceful, Labeled regular digraph, Biological networks.

Introduction

The theory of complex networks plays an important role in the bio medical and bio chemical fields. For an example we can consider the issue of protein functioning. Having different methods, one of the finest methods to show the protein functions together is graphical method. We can use directed graphs to represent the interactions between different entities such as proteins, chemicals or macro molecules and can also use to describe biological pathways. In 1965 Rosa introduced the concept of labelling of graphs. In 1980 bloom and Hsu defined libelling for digraphs and opened the new door.

By labelling we mean that assigning integers to vertices or edges or to both according to certain conditions [1]. Rosa [2] introduced the notion of graceful labelling. Bloom et al. [3,4] extended the concept of graceful labelling for digraphs also. Lo [5] defined the new labeling called edge graceful labelling. Gayathri et al. discussed the strong edge graceful labelling [6]. Thamizharasi [7] and Rajeswari et al. [8] studied graceful and magic labelling of Cayley digraphs. Labelled digraphs are currently the most used networks throughout the field of bio informatics. They can provide valuable insight into the internal organization of a biological network.

Preliminaries

In this section we define the edge graceful labelling methods for digraphs and also present the basic definitions which would be essential to prove our results.

Definition 2.1

A digraph is said to be edge graceful if there exists a bijection f: E→{1,2….│E│} such that the induced mapping f*=: V → {0,1,2…│V│ -1} is given by f* (vi)=(Σf (e_ij)) (mod│V│) taken over all the outgoing arcs of vi is a bijection where e_ij is the j^th outgoing arc of the vertex v_i.

Definition 2.2

A digraph is said to be strong edge graceful if there is an injection f:E→{1,2,3….3(|E|/2)} such that the induced mapping f* (v_i)=(Σf (e_ij)) (mod 2│V│) taken over all the outgoing arcs of v_i is an injection, where e_ij is the j^th outgoing arc of the vertex v_i.

Definition 2.3

An antimagic digraph is a digraph with e arcs labelled with distinct elements of {1,2,3,…,e} so that the sum of the labels of the outgoing arcs at each vertex differ.

Main Results

In this section we show that the regular digraph satisfies all the edge graceful techniques which are defined in the above section and we provide some examples too.

Theorem 3.1

Every m regular digraph admits Edge graceful labeling if m ≡ 1 (mod 2).

Proof:

Let the m regular digraph G (V,E) has n vertices and every vertex has m outgoing and m incoming arcs. Therefore the digraph totally has mn arcs. Denote the vertex set of G as V={v₁,v₂,…,v_n} and edge set of G as E={e₁₁,e₁₂, …,e_1m,e₂₁,e₂₂,…,e_2m,…,e_n1,…,e_nm} where e_ij is j_th outgoing arc from i_th vertex.

To show that the regular digraph admits edge graceful labeling, we have to show that there exists a bijection f: E → {1,2, ….│E│}such that the induced mapping f*: V → given {0,1,2, ……,│V│-1} by f* (vi)=(Σ ^m j=1 f(e_ij)) (mod │V│) is a bijection. Where e_ij is the j_th outgoing arc of the vertex v_i.

Since, m ≡ 1 (mod 2) m is odd.

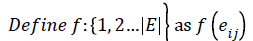
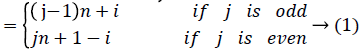
Then the induced function f*: V → {0,1,2,……,│V│-1} given by, for each v_i

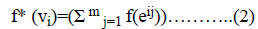
=i+2n+1-i+2n+i+4n+1-i+….+ (m-1)n+i

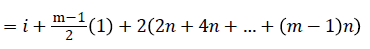
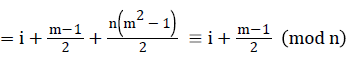
Since m is constant, f*(v_i) is distinct for every I, 1 ≤ i ≤ p.

Since m is constant, f*(vi) is distinct for every I, 1 ≤ i ≤ p.

Proposition 3.2

Every edge graceful regular digraph G with │G│=n and m ≡ 1 (mod 2) for 1 ≤ i ≤ n is a an antimagic.

Proof

From the above theorem we know that the regular digraph with odd number of outgoing arcs is edge graceful. Now we have to prove that it is antimagic too.

Define f and f* as in equations (1) and (2) of the above theorem respectively. We have

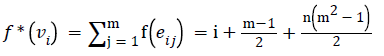
Since m and n are constants, f*(v_i) is distinct for every i, 1 ≤ i ≤ n.

Hence the edge graceful Cayley digraph is always antimagic.

Theorem 3.3

Every Regular digraph admits strong edge graceful labelling.

Proof

Let the regular digraph with n vertices and m outgoing arcs from each vertex and define the edge set and vertex set as in the previous theorem 3.1. To show that the digraph admits strong edge graceful labeling, we have to show there exists an injection f: E →{1,2,3…3(|E|/2)} such that the induced mapping given by 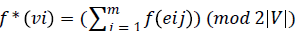is an injection. Where eij is the jth outgoing arc of the vertex vi. We prove this theorem in two cases.

Case (i): if m ≡ 1 (mod 2)

Define f: E →{1,2,3…3(|E|/2)}as

Then the induced function

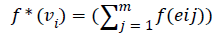
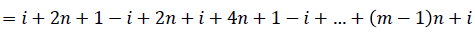
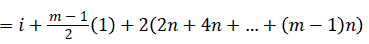
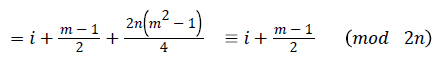
Since m is constant, f*(vi) is distinct for every i, 1 ≤ i ≤ n

Hence the Regular digraph is strong edge graceful if m ≡ 1 (mod 2).

Case (ii): if m ≡ 0 (mod 2)

Define f : E → {1,2,3…3(|E|/2)}as

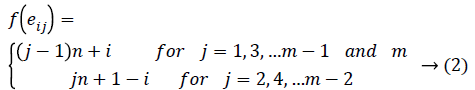
Then the induced function

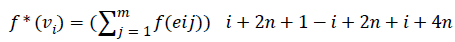
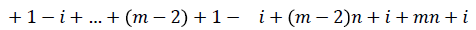
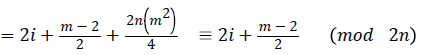
Since m is constant, f*(vi) is distinct for every i 1 ≤ i ≤ n.

Threrefore the Regular digraph is strong edge graceful for even number of outgoing arcs also. Hence every Regular digraph is strong edge graceful.

Corollary 3.4

Every edge graceful Cayley digraph is strongly edge graceful. Since the Regular digraph with even number of generators is not edge graceful, the converse is not true.

Application of labelled digraphs to visualize the hydrogen bond networks in protein structures

The most important feature of the hydrogen bond is that it possesses direction and hence hydrogen bond networks along with cooperativity and anti-cooperativity can be represented by directed graphs [9]. Hydrogen bond networks can be represented by digraphs, where vertices correspond to donor and acceptor group, and arcs correspond to hydrogen bonds from proton-donor to proton-acceptor and can be labeled. It also includes directed edges or arcs labelling which display available geometrical information about hydrogen bond.

Conclusion

The mathematical division which is used in the study of complex networks in biological field is graph theory. In this paper we provided labelling on regular digraphs and explained the applications of labelled digraphs in the field of bio informatics. Some of the problems that can be explored include the development of topological indices based on the spectra of protein graphs so as to identify and classify protein folds in the database.

References

1. Gallian JA. A dynamic survey of graph labelling. Elect J Combinatorics 2016.
2. RosaA. On certain valuations of the vertices of the Graphs. International Symposium on Theory of graphs, Rome 1966.
3. Bloom GS, Hsu DF. On graceful directed graphs, SIAM Jo. Alg Discrete Mathematics 1985; 6: 519-536.
4. Bloom GS, Hsu DF. On graceful digraphs and a problem of network addressing. CongrNumer 1982; 35: 91-103.
5. Lo S. On edge graceful labelings of graphs. CongrNumer 1985; 50: 231-234.
6. Gayathri B, Subbiah M. Strong edge graceful labelings of some graphs. Bull Pure ApplSci 2008; 27:89-98.
7. Thamizharasi R, Rajeswari R. Graceful and Magic labeling on Cayley digraphs. Int J Math Anal 2015; 9: 947-954.
8. Thamizharasi R, Rajeswari R. Labelings of Cayley Digraphs andits Line Digraphs. Int J Pure Appl Math 2015; 101: 681-690.
9. Tiwari A, Tiwari V. Graph Theory based visualization of hydrogen bond networks in protein structure. Bio Informa 2007.