Research Article - Biomedical Research (2018) Volume 29, Issue 16
An intelligent skull stripping algorithm for MRI image sequences using mathematical morphology
Kavitha Srinivasan* and Nanditha NM
School of Electrical and Electronics Engineering, Sathyabama University, Chennai, India
- *Corresponding Author:
- Kavitha Srinivasan
School of Electrical and Electronics Engineering
Sathyabama University, India
Accepted on August 21, 2018
DOI: 10.4066/biomedicalresearch.29-18-949
Visit for more related articles at Biomedical ResearchAbstract
Brain tumor is a dreadful disease which occurs when abnormal cells form uncontrollably. The modality adopted to detect abnormalities is Magnetic Resonance Imaging (MRI). MRI brain images contain nonbrain tissues. One of the important preprocessing steps is the whole brain segmentation, the process of skull stripping which isolates brain tissue and non-brain tissue. Segmentation is tedious and consumes more time only well experienced radiologist or a clinical expert can perform it with best accuracy. In order to overcome these limitations, computer aided medical diagnosis is essential. In this work, an intelligent and a robust skull stripping algorithm using mathematical morphology suited for all types of MR sequences is proposed. The method was validated on the international database collected from whole brain Atlas. The performance was evaluated using the metrics Jaccard Similarity Coefficient (JSC), Dice Similarity Coefficient (DSC), False Positive Rate (FPR), False Negative Rate (FNR), sensitivity, specificity and accuracy. An average of 97.25% indicates better overlap between proposed skull stripping and manual stripping by radiologists as a gold standard. The simulation results proved high accuracy in comparison to the ground truth results which is evident from the similarity coefficient metrics.
Keywords
Magnetic resonance imaging, Brain segmentation, Morphological operation, Similarity measure.
Introduction
Brain is the most complex structure of our human body. Grey matter consists of neuronal cell bodies, neurophil, glial cells, synapses and capillaries which is the major component of the central nervous system. White matter is made up of myelinated axons called tracts. Grey matter contains numerous cell bodies and has few myelinated axons. Brain is surrounded by tissue membrane called meninges which separates brain from skull. CSF is a colorless body fluid that exists in the brain and spinal cord. CSF acts as a cushion and provides immunological protection to the brain [1,2].
Computer aided medical diagnosis with various image processing techniques has increased the possibility of accurate prediction due to better visualization. Amongst the various tools, MRI (magnetic resonance image) is an effective imaging tool, to study the anatomical structure due to its high spatial resolution. Conventional MR sequences are T1-weighted, T2- weighted, and PD-weighted. T1-weighted has highest signal on fat tissue and hence better suited for showing anatomical structures. T2-weighted has highest signal in liquid and hence suited for detecting lesions. PD-weighted is suited for characterizing lesions by differentiating the contrast of the brain tissues [3]. MRI images brain in axial, coronal and sagittal planes. MRI scans can produce detailed pictures of organs, soft tissues, bone and other internal body structure [4,5].
Artifacts introduced during acquisition and undesired tissues affect the processing quality and lead to inaccurate diagnosis. Thus, an important preprocessing step is skull stripping where the brain tissue is segmented from the skull. Since the manual segmentation is very time consuming and prone to errors, various methods have been developed to automatically remove extra-cerebral tissues without human intervention. Morphometric studies require a preprocessing procedure to isolate the brain from extra-cranial known as skull stripping [6-9]. Skull stripping ensures better segmentation and assures accurate diagnosis of brain diseases and probability of misclassification of abnormal tissues is also reduced. Numerous skull stripping algorithms are available in the literature. Several studies are being carried out on the available skull stripping procedures and their performance is analysed on the standard research datasets. Every algorithm has its own merits and limitations. In this work, a robust skull stripping algorithm that is suited for all types of MR image sequences has been developed.
Related Works
From literatures, it is observed that skull stripping can be performed by morphological operation, intensity based operation, deformable surface based operation or a combination of all the methods. Galdame et al. [10] suggested skull stripping procedure by deformable models and histogram analysis. Deformable models work on simplex mesh which is controlled by local gray levels. The performance is compared with three conventional skull stripping methods such as brain extraction tool, brain surface extractor, and hybrid watershed algorithm.
Brummer et al. [11] developed automatic detection of brain contour with a histogram-based thresholding and conventional morphological operations with image intensity correction procedure. Anatomical knowledge is used to discriminate desired and undesired structures. Gao et al. [12] proposed a sequence where anisotropic diffusion filtering with edge detection and morphological operation smoothens noisy region, identifies the anatomical boundaries and selects the pixel that correspond to the brain tissue.
Shattuck et al. [13] proposed anisotropic diffusion filtering combined with edge detection, and mathematical morphology to remove skull. 2D Marr-Hildreth operator performs edge detection and low-pass filtering is performed with Gaussian kernel. Hahn et al. [14] proposed watershed algorithm based skull stripping which may lead to over-segmentation. Suri [15] suggested an active contour algorithm where fuzzy membership function is used to classify brain images.
Atkins et al. [16] suggested template based method which separates brain and non-brain regions effectively. It varies with the type of templates used for separation and also on the application of atlases. Leung et al. [17] performed multi-atlas propagation by combining many segmentations performed by atlas registration.
Huang et al. [18] suggested extraction of brain from T1- weighted images through hybridization of expectation maximization algorithm with mathematical morphology and connected component analysis and brain border is found using geodesic active contours.
Materials and Methods
Patient details and data acquisition
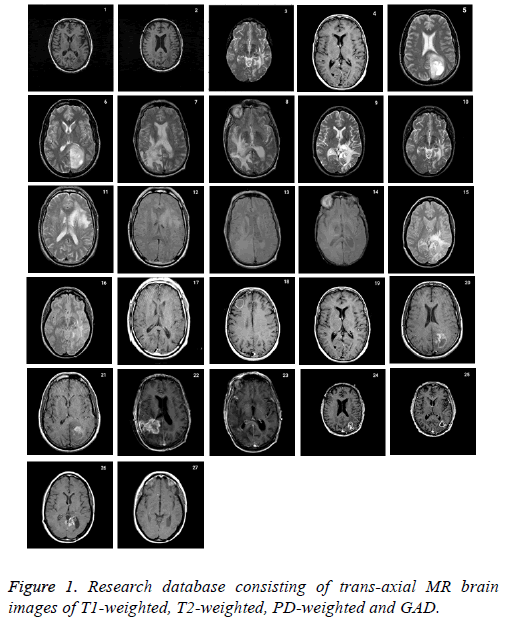
Research database consists of 27 datasets of 6 patients with age between 35-71 with anaplastic astrocytoma, grade IVastrocytoma, low grade glioma, meningioma with T2- and PDweighted MR, metastatic carcinoma with T2-weighted MR and grade II- astrocytoma with T1-weighted MR collected from the whole brain atlas-Harvard Medical school database (http:// med.harvard.edu/aanlib\) is used to validate the proposed skull stripping algorithm. The RGB image is converted into grayscale before processing. All of the images had 256 × 256 pixels acquisition matrices, and 2 slices from each patient was collected. The imaging protocol used a 3 T MRI scanner with slice thickness of 1 or 3 mm. The standard slice orientation of trans-axial is considered. Figure 1 represents the complete set of database acquired.
Mathematical morphology
To analyse geometrical structures such as size, shape, connectivity, mathematical morphology is a tool used which is based on set theory. It was developed originally for binary images but can be used for grayscale and color images. It is a collaborative work of Georges et al. at the École des Mines de Paris, France. The procedure is to search the image at different locations with a pre-defined shape and to decide as how this shape fits or misses the shapes in the image. This is called the structuring element, and it is also a binary image. Choice of size and shape of structuring element is need based. Diamond, square, disc, horizontal line, vertical line, cross etc. are the most commonly used structuring element, erosion and dilation are the two essential operations in mathematical morphology. Other operations like opening and closing can be derived from it.
Erosion and dilation
Let I be the binary image. S is the structuring element. Erosion of I by the structuring element S is denoted by IƟS. It denotes the set of all pixels which S placed at that pixel is contained within I. Erosion shrinks or performs thinning of the object. It excludes all small unwanted objects in the image.
IƟS={z ǀ(S) z ⊆ I} → (1)
Dilation of I by the structuring element S is denoted by I ⊕ S. I overlaps by at least one element. Dilation performs thickening of an image. It highlights small objects in the image.
I ⊕ S=*z ǀ( ̂) z ∩ I ≠ ϕ} → (2)
Opening and closing
Opening operation denoted by I • S smoothens the contour of an object and breaks the narrow lines. In opening operation erosion is performed followed by dilation
I • S=(A Ɵ S) ⊕ S → (3)
Closing operation denoted by I • S smoothens the contours. It eliminates discontinuity and small gaps between the objects. In closing operation, dilation is performed followed by erosion.
I • S=(A ⊕ S) Ɵ S → (4)
Proposed skull stripping algorithm
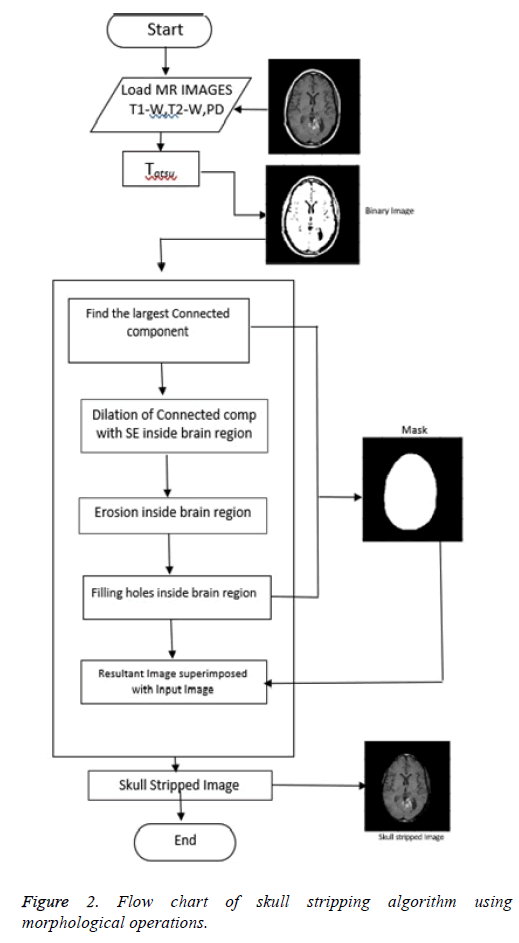
Proposed skull stripping algorithm works on morphological operations [19-21]. With morphological operation, extra information is eliminated and used to focus on the area of interest [22-24]. Structuring Element (SE) is so chosen to have size and shape according to the type of MR image sequence. For each pixel location, morphological operation is performed between SE and MR image. Figure 2 shows the flowchart of the algorithm using morphological operations.
Step 1: Conversion to binary image: The input image is converted to binary image with Otsu’s thresholding [24]. Otsu's method automatically performs reduction of a gray level image to a binary image. The algorithm considers the image as two classes of pixels, foreground pixels and background pixels. Optimum threshold is obtained which separates the two classes so that their intra-class variance is minimal and their inter-class variance is maximal.
Step 2: Creation of mask: Brain is the largest connected component. This component is extracted from the binary image. Dilation and erosion operations are performed to preserve the minute features of the brain in the resultant image. By filling the holes, the brain becomes a complete connected component.
Step 3: Superimposition: The final skull stripped image is obtained by superimposing the mask on the input image.
Results and Discussion
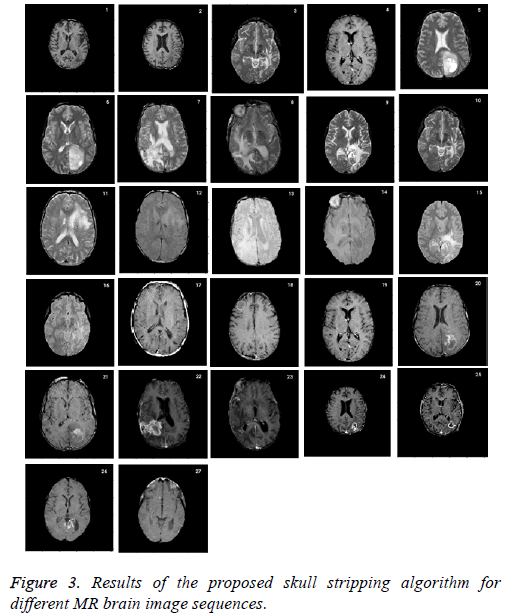
Skull stripping is a challenging pre-processing step in tumor characterization due to intrinsically imprecise nature of brain image. It helps to remove the skull from the input image. The performance of the proposed approach is compared with ground truth which is a manual stripping by a well experienced radiologist considered as gold standard. Figure 3 shows the results of the proposed skull stripping algorithm for different MR brain image sequences. The algorithm is carried out by using Matlab tool kit.
Seven performance metrics namely, Jaccard similarity coefficient (JSC), Dice similarity coefficient (DSC), false positive rate (FPR), false negative rate (FNR), sensitivity, specificity and segmentation accuracy have been calculated. JSC and DSC measure the similarity between ground truth and skull stripped images. The confusion matrix in terms of TP, TN, FP, and FN between the expected output and ground truth are shown in Table 1. TP represents the number of pixels that are correctly classified as brain tissue; TN is the number of pixels that are correctly classified as non-brain tissue; FP is the number of pixels that are in-correctly classified as brain tissue and FN is the number of pixels that are in-correctly classified as non-brain tissue [25-27], JSC can be formulated according to the following equation
| Expected outcome | Ground truth | Row total | |
|---|---|---|---|
| Positive | Negative | ||
| Positive | TP | FP | TP+FP |
| Negative | FN | TN | FN+TN |
| Column total | TP+FN | FP+TN | TP+FP+FN+TN |
Table 1. Confusion matrix defining the terms TP, TN, FP, FN.
Jaccard coefficient JSC (A, B)=(A ∩ B)/(A ∪ B) → (5)
=2TP/2TP+FP+FN
where A is the area of the brain region in the ground truth skull-stripped image and B is the area of the brain region of the corresponding image with the proposed skull stripping algorithm. If JSC is 1, it represents complete overlap, whereas an index of 0 represents that there are no overlapping pixels.
DSC is used to describe the overall level of similarity between proposed skull-stripped algorithm and ground truth. DSC has been calculated according to the following equation
Dice coefficient DSC (A, B)=2 (A ∩ B)/|A|∪|B| → (6)
=TP/TP+FP+FN
False positive rate (FPR) and false negative rate (FNR) were used to quantify over and under segmentation. Both FPR and FNR were calculated according to
False positive rate FPR (A, B)=(A/B)/(A ∪ B) → (7)
=FP/TN+FP
False negative rate FNR (A, B) = (B/A)/(A ∪ B) → (8)
=FN/TP+FN
A direct relation between JSC, FPR, and FNR is according to the following expression:
Jaccard coefficient JSC (A, B)=1-FPR-FNR → (9)
Sensitivity=FP/TN+FP → (10)
Specificity=TN/TN+FP → (11)
Accuracy=TP+TN/TP+TN+FP+FN → (12)
The performance metrics evaluated for the proposed skull stripping algorithm is given in Table 2. The proposed method is robust and hence successfully strips the skull for all types of brain image sequences. Average performance using dice coefficient is 97.25% and using Jaccard coefficient is 94.87% which illustrates that highest similarity or overlap between the skull stripping algorithm proposed and the ground truth.
| Subject | Jaccard coefficient | Dice coefficient | Similarity | Specificity | Accuracy |
|---|---|---|---|---|---|
| T1_ weighted | 0.8012 | 0.8896 | 0.8059 | 1 | 0.9995 |
| T1_ weighted | 0.8585 | 0.9239 | 0.9502 | 0.9995 | 0.9993 |
| T2_ weighted | 0.9482 | 0.9734 | 0.973 | 0.9981 | 0.9964 |
| T2_ weighted | 0.9982 | 0.9991 | 0.999 | 0.9999 | 0.9998 |
| T2_ weighted | 0.9592 | 0.9792 | 0.9896 | 0.9975 | 0.997 |
| T2_ weighted | 0.9964 | 0.9982 | 0.9992 | 0.9998 | 0.9997 |
| T2_ weighted | 0.9987 | 0.9993 | 0.9992 | 0.9999 | 0.9998 |
| T2_ weighted | 0.9986 | 0.9993 | 0.9992 | 0.9999 | 0.9998 |
| T2_ weighted | 0.9649 | 0.9822 | 0.9653 | 0.9999 | 0.9922 |
| T2_ weighted | 0.9752 | 0.9875 | 0.9756 | 0.9999 | 0.9945 |
| T2_weighted | 0.9953 | 0.9976 | 0.9988 | 0.9991 | 0.9991 |
| PD-weighted | 0.9804 | 0.9901 | 0.9812 | 0.9998 | 0.9963 |
| PD-weighted | 0.9871 | 0.9935 | 0.9873 | 0.9999 | 0.9972 |
| PD-weighted | 0.9772 | 0.9885 | 0.9772 | 1 | 0.9989 |
| PD-weighted | 0.9869 | 0.9934 | 0.9931 | 0.9998 | 0.9996 |
| PD-weighted | 0.9143 | 0.9552 | 0.9154 | 0.9968 | 0.9918 |
| GAD | 0.9616 | 0.9804 | 0.9641 | 0.9997 | 0.9962 |
| GAD | 0.9658 | 0.9826 | 0.9684 | 0.9997 | 0.9971 |
| GAD | 0.8058 | 0.8925 | 0.9453 | 0.9967 | 0.9957 |
| GAD | 0.9293 | 0.9634 | 0.9962 | 0.9991 | 0.9991 |
| GAD | 0.7454 | 0.8541 | 0.7788 | 0.9998 | 0.9987 |
| GAD | 0.9813 | 0.9905 | 0.9905 | 0.9998 | 0.9996 |
| GAD | 0.9894 | 0.9942 | 0.9902 | 0.9997 | 0.9983 |
| GAD | 0.9799 | 0.9899 | 0.9807 | 0.9999 | 0.9972 |
| GAD | 0.9683 | 0.9839 | 0.9687 | 0.9999 | 0.9929 |
| GAD | 0.976 | 0.9879 | 0.9769 | 0.9997 | 0.9946 |
| GAD | 0.9722 | 0.9859 | 0.9797 | 0.9968 | 0.9918 |
| Average performance | 0.9487 | 0.9725 | 0.9648 | 0.9992 | 0.9971 |
Table 2. Performance of skull stripping algorithm.
Conclusion
Skull stripping being a preliminary step, its accuracy is a key factor. Most of the methods suggested in literature cannot be applied for all brain image sequences and orientations. In this paper, an intelligent skull stripping algorithm that works well for all types of MR Image sequences such as T1, T2, PD, and GAD is proposed. Experimental results confirm the efficacy of the proposed algorithm. Moreover comparison with ground truth showed that the proposed approach is promising in obtaining high performance metrics.
References
- Purves D, Augustine GJ, Fitzpatrick D, Hall WC, Lamantia AS, McNamara JO, White LE. Neuroscience (4th Edn.). Sinauer Assoc 2008; 15-16.
- Blumenfeld H. Neuroanatomy through clinical cases (2nd Edn.). Sunderland, Mass.: Sinauer Assoc 2010; 21.
- Haacke EM, Brown RW, Thompson MR, Venkatesan R. Magnetic resonance imaging, physical principles and sequence design. John Willey Sons NY 1999.
- Quencer RM, Bradley WG. MR imaging of the brain: what constitutes the minimum acceptable capability? AJNR Am J Neuroradiol 2001; 22: 1449-1450.
- Cheour M. Advantages of brain MRI. Radiology Org 2010.
- Fennema-Notestine C, Ozyurt IB, Clark CP, Morris S, Bischoff-Grethe A, Bondi MW, Jernigan TL, Fischl B, Segonne F, Shattuck DW, Leahy RM, Rex DE, Toga AW, Zou KH, Brain M, Brown GG. Quantitative evaluation of automated skull-stripping methods applied to contemporary and legacy images: effects of diagnosis, bias correction and slice location. Hum Brain Mapp 2006; 27: 99-113.
- Matsumoto S, Asato R, Konishi J. A fast way to visualize the brain surface with volume rendering of MRI data. J Digit Imaging 1999; 12: 185-190.
- Mahmood Q, Chodorowski A, Mehnert A, Gellermann J, Persson M. Unsupervised Segmentation of Head Tissues from Multi-modal MR Images for EEG Source Localization. J Digit Imaging 2015; 28: 499-514.
- Hata Y, Kobashi S, Kondo K,Kitamura YT, Yanagida T. Transcranial ultrasonography system for visualizing skull and brain surface aided by fuzzy expert system. IEEE Trans Syst Man Cybern 2005; 35: 1360-1373.
- Benson CC, Lajish VL, Kumar R. A novel skull stripping enhacement algorithm for the improved brain tumor segmentation using Mathematical morphology. Int J Image Graph Sig Proc 2016; 7: 59-66.
- Ahmad C, Camel T. Quantitative evaluation of robust skull stripping and tumor detection applied to axial MR images. Brain Inform 2016; 3: 53-61.
- Otsus N. A threshold selection method from gray level histograms? IEEE Transac Sys MAN Cybern 1979; 9.
- Torheim T, Malinen E, Kvaal K, Lyng H, Indahl UG, Anderson EKF, Futsaether CM. Classification of dynamic contrast enhanced MR images of cervical cancers using texture analysis and support vector machines. IEEE Trans Med Imaging 2014; 33: 1648-1656.
- Dhanalakshmi K, Rajamani V. An intelligent mining system for diagnosing medical images using combined texture histogram features. Int J Imaging Sys Technol 2013; 23: 194-203.
- Rajendran P, Madheswaran M. Pruned associative classification technique for the medical image diagnosis system. Proc 2nd Int Conf Mac Vis 2009; 293-297.
- Kalavathi P, Prasath VB. Methods on skull stripping of MRI head scan images-a review. J Digit Imaging 2016; 29: 365-379.
- Brummer ME, Mersereau RM, Eisner RL, Lewine RJ. Automatic detection of brain contours in MRI data sets. IEEE Trans Med Imaging 1993; 12: 153-166.
- Gao J, Xie M. Skull stripping MR brain images using anisotropic diffusion filtering and morphological processing. Proc Int Sym Comp Netw Multimed Technol Wuhan 2009; 1: 1-4.
- Shattuck DW, Sandor-Leahy SR, Schaper KA, Rottenberg DA, Leahy RM. Magnetic resonance image tissue classification using a partial volume model. Neuroimage 2001; 13: 856-876.
- Hahn HK, Peitgen HO. The skull stripping problem in MRI solved by single 3D watershed transform. Proc Med Image Comput Comp Assist Interv 2000; 134-143.
- Suri JS. Two-dimensional fast magnetic resonance brain segmentation. IEEE Eng Med Biol Mag 2001; 20: 84-95.
- Ali P, Ramezani M, Ghadimi N. A hybrid neural network-gray wolf optimization algorithm for melanoma detection. Biomed Res 2017; 28: 8.
- Razmjooy N, Mehdi R, Noradin G. Imperialist competitive algorithm-based optimization of neuro-fuzzy system parameters for automatic red-eye removal. Int J Fuzzy Sys 2017; 19: 1144-1156.
- Razmjooy N, Sheykhahmad FR, Ghadimi N. A hybrid neural network-world cup optimization algorithm for melanoma detection. Op Med 2018; 13: 9-16.
- Atkins MS, Siu K, Law B, Orchard JJ, Rosenbaum WL. Difficulties of T1 brain MRI segmentation techniques, medical imaging. Proc SPIE 2001; 4684: 1837-1844.
- Leung KK, Barnes J, Modat M, Ridgway GR, Bartlett JW, Fox NC, Ourselin S. Brain MAPS: an automated, accurate and robust brain extraction technique using a template library. Neuroimage 2011, 55: 1091-1108.
- Huang A, Abugharbieh R, Tam R, Traboulsee A. MRI brain extraction with combined expectation maximization and geodesic active contours. Proc. IEEE Int Symp Signal Proc Inf Technol 2006; 107: 107-111.