Research Article - Biomedical Research (2017) Artificial Intelligent Techniques for Bio Medical Signal Processing: Edition-I
A statistical model and an algorithm for diffusion tensor smoothing in impulse and mixed noise situations
Resmi R Nair1,2*, Sivakumar Rajagopal1 and Ebenezer David21RMK Engineering College, Chennai, India
2Anna University, Chennai, India
Accepted date: March 11, 2017
Abstract
Image smoothing is a prerequisite for subsequent operations in image processing. There are several techniques for image smoothing among which diffusion tensor smoothing is preferred in imaging the brain, muscles, heart, tumour and cancer cells. Data acquisition and transmission introduce impulse noise along with the ever present Gaussian noise. Image smoothing filters such as the mean filter, anisotropic diffusion filter, the bilateral filter and the guided filter are not intrinsically robust to impulse noise. They require additional complex structures for robustness. The robustness of diffusion tensor smoother has not been well studied. A statistical model for diffusion tensor image smoother is proposed consistent with the model for the standard anisotropic diffusion smoother. An algorithm is derived. The performance of the diffusion tensor smoother is investigated qualitatively and quantitatively. The intrinsic robustness of the diffusion tensor smoother and the superior performance thereof in comparison with the anisotropic diffusion are demonstrated.
Keywords
Diffusion tensor smoothing, Robustness, Anisotropic diffusion, Mixed noise
Introduction
Magnetic Resonance Imaging (MRI) is useful in visualizing the internal structures of the body. It provides good contrast between different soft issues of the body. Images including MRI are contaminated by a variety of noise during acquisition, storage and transmission. Two primary noise types are Gaussian noise and Impulse noise. Noise reduction is achieved by image smoothing. Prominent image smoothing filters are the mean filter [1], the Bilateral filter [2], the Guided filter [3], diffusion smoothing filter [4] and diffusion tensor smoother [5]. Diffusion tensor smoothing forms the mathematical basis of MRI which is useful in the study of molecular diffusion which reveals microscopic details about the body tissues. Diffusion tensor imaging is extensively used in the detailed analysis of MRI images in recent research [6,7]. Three important requirements in diffusion tensor imaging are smoothing, detail preservation, and edge preservation. Digital data acquisition and transmission introduce impulse noise and, therefore, the robustness of diffusion tensor image smoothing to impulse noise is also an important requirement. Importance of robustness as a desirable property of smoothing filters in the presence of impulse noise is well recognized [8-16]. However, the robustness of diffusion tensor imaging has not been well studied. The primary objective of this paper is to investigate the intrinsic robustness of diffusion tensor smoothing in impulse and mixed noise situations where Gaussian plus impulse noise are present. This investigation takes the standard anisotropic diffusion smoothing as a reference, since the anisotropic diffusion smoothing, introduced by Perona and Malik [4], has become one of the foundational techniques for smoothing with edge preservation. A statistical model for the purpose of the investigation of the robustness of the diffusion tensor smoothing consistent with the standard anisotropic diffusion smoothing is presented. An algorithm for numerical computing is derived. The performance of the diffusion smoother is studied in comparison with that of the anisotropic diffusion smoother. Results are presented in terms of quantitative and qualitative metrics.
A Statistical Model for Diffusion Tensor Smoothing
The anisotropic diffusion equation with a convex energy functional is given by
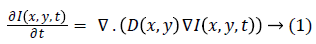
The corresponding discrete version is
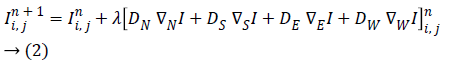
Where four gradients 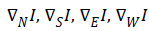 are along North, South, East and West directions, λ is a constant, DN, DS, DE and DW are the diffusion coefficients, i,j are spatial indices and is the time index. Rewriting equation (2) as
are along North, South, East and West directions, λ is a constant, DN, DS, DE and DW are the diffusion coefficients, i,j are spatial indices and is the time index. Rewriting equation (2) as
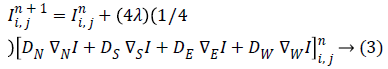
Equation (3) can be rearranged as
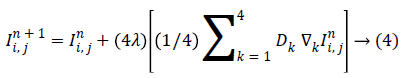
If Dk are functions of gradients 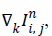 that is,
that is,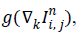 equation (4) can be written as
equation (4) can be written as
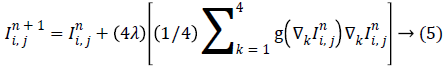
Equation (5) now represents the anisotropic diffusion smoothing as a statistical model where the term within the square brackets represents weighted averaging which is a maximum likelihood (ML) estimate in the L2 sense. Let 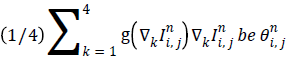 so that
so that
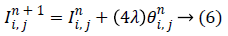
Equation (6) is a statistical model which characterizes a first order Markov process. If 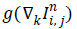 is semi group [17,18], equation (6) represents an irreversible process. Different formulations of anisotropic diffusion should have a fundamental form as expressed by (6). The non-linear tensor diffusion process can be described by
is semi group [17,18], equation (6) represents an irreversible process. Different formulations of anisotropic diffusion should have a fundamental form as expressed by (6). The non-linear tensor diffusion process can be described by 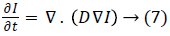
where I is the image intensity I(x,y,t), D is the diffusion tensor and the RHS is the divergence of the gradient of I. The diffusion tensor is represented as 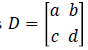 where a, b, c and d can be obtained in terms of image intensity values [5]. Equation (7) can now be expressed as
where a, b, c and d can be obtained in terms of image intensity values [5]. Equation (7) can now be expressed as

By recasting equation (8) in the form of the statistical model (6), 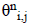 for diffusion tensor is derived as
for diffusion tensor is derived as
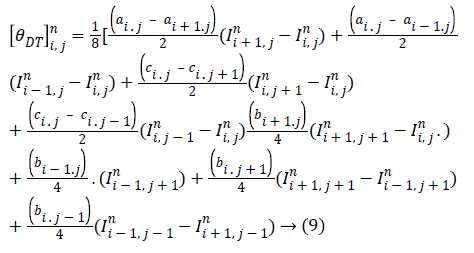
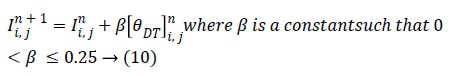
The model is stable over 0<β ≤ 0.25 in the numerical environment consistent with (6) where 0< λ ≤ 0.25.
Results and Discussion
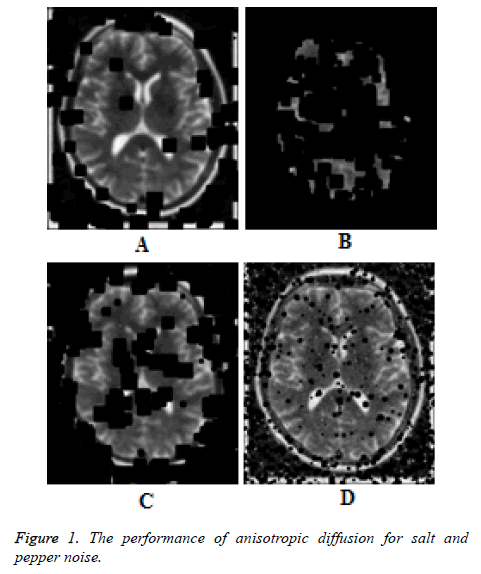
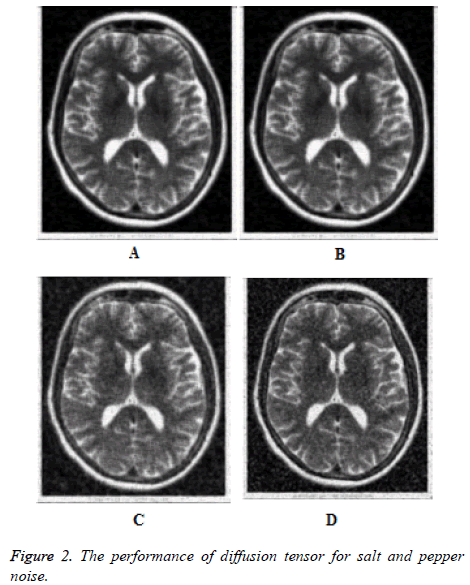
The performance of the diffusion tensor smoother is studied in comparison with the foundational anisotropic diffusion algorithm introduced by Perona and Mailk [4]. Figures 1a-1c show the results for anisotropic diffusion smoother for impulse noise of density 5%, 10% and 20% respectively for 25 iterations. The spreading of black patches clearly indicates the sensitivity of the algorithm to impulse noise (salt and pepper noise). Even though the robustness has been established in theory for Perona-Malik algorithm [6], the results show that the algorithm is not intrinsically robust. However, for low number of number of iterations (Figure 1d), the Perona-Malik algorithm is stable, but the noise removal capability is very poor. The performance of the diffusion tensor smoother is shown in Figures 2a-2c for impulse noise of density 5%, 10% and 20% respectively for 25 iterations. The good impulse noise removal capability and the intrinsic robustness are clearly demonstrated. Figure 2d shows the performance at 20% salt and pepper noise for 10 iterations. It is clear that the diffusion tensor smoother is intrinsically robust.
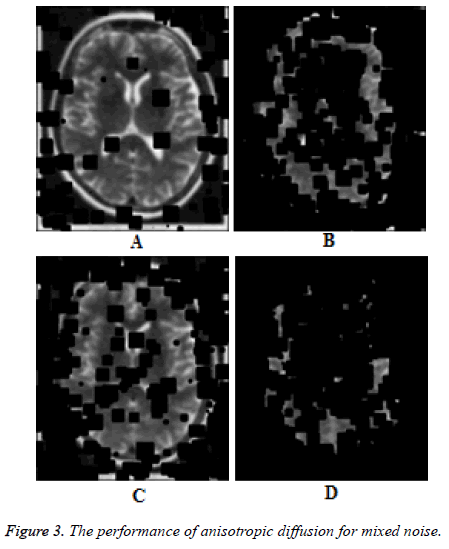
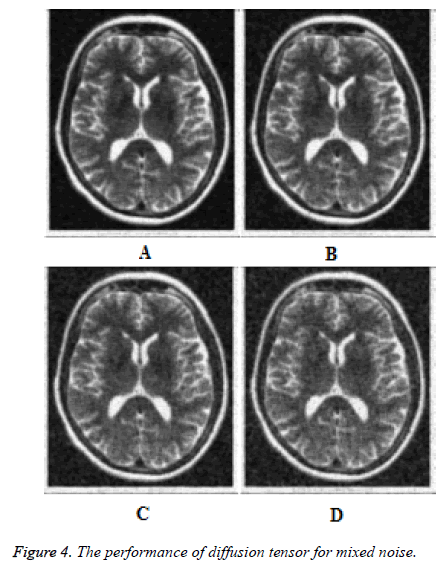
Figures 3a-3d show the results for anisotropic diffusion smoother for mixed noise with Gaussian noise of variance 0.01and salt and pepper noise of density 5%, 10%, 15% and 20% respectively for 25 iterations. It is clearly seen from these results that the anisotropic diffusion exhibits spreading effect as black patches and the mixed noise removal capability is very poor. The performance of the diffusion tensor smoother is shown in Figures 4a-4d for mixed noise with Gaussian noise of variance 0.01and salt and pepper noise of density 5%, 10%, 15% and 20% respectively for 25 iterations. It can be seen form these results that that the diffusion tensor smoother works well for mixed noise. Table 1 displays the peak signal to noise ratio (PSNR) and the structural similarity index metric (SSIM) for impulse noise of density 5%, 10% and 20% respectively for 25 iterations. The quantitative results confirm the superiority of the diffusion tensor smoother over the anisotropic diffusion smoother in terms of edge preservation and noise removal.
| Methods | PSNR | SSIM | ||||
|---|---|---|---|---|---|---|
| 5% | 10% | 20% | 5% | 10% | 20% | |
| Perona | 10.8654 | 8.4718 | 7.3038 | 0.7440 | 0.5824 | 0.2626 |
| tensor | 18.7633 | 18.0952 | 16.6287 | 0.8132 | 0.7768 | 0.6923 |
Table 1. Performance metrics.
Conclusion
A statistical model for diffusion tensor image smoothing and an algorithm are proposed. The intrinsic robustness of the diffusion tensor smoother is investigated. The performance of the diffusion tensor in terms of the statistical model and the corresponding algorithm are also investigated in impulse noise and mixed noise situations. The standard anisotropic diffusion smoother has been employed as a reference. The results are obtained in terms of the standard image processing metrics and visuals for Magnetic Resonance Image (MRI). The intrinsic robustness, the smoothing capability and the edge preserving capability of the diffusion tensor smoother are demonstrated.
References
- Rakshit S, Ghosh A, Uma Shankar B. Fast mean filtering technique (FMFT). Pattern Recognit 2007; 40: 890-897.
- Paris S, Kornprobst P, Tumblin J, Durand F. Bilateral Filtering: Theory and Applications. Compute Graphics Vision 2008; 4: 1-73.
- He K, Sun J, Tang X. Guided image filtering. IEEE Trans Pattern Anal Mach Intell 2013; 35: 1397-1409.
- Perona P, Malik J. Scale space and edge detection using anisotropic diffusion. IEEE Trans Pattern Anal Machine Intell 1990; 12: 629-639.
- van den Boomgaard R. Algorithms for Non-Linear Diffusion Matlab in a Literate Programming style. In: Intelligent Sensory Information Systems. University of Amsterdam, 2001.
- Liu X, Yuan Z, Guo Z and Xu. D. A localized Richardson-Lucy algorithm for fiber orientation estimation in high angular resolution diffusion imaging. Med Phys 2015; 42: 2524-2539.
- Liu J, Gasbarra D, Railavo J. Fast estimation of diffusion tensors under Rician noise by the EM algorithm. J Neurosci Methods 2016; 257: 147-158.
- Black MJ, Sapiro G, Marimont DH, Heeger D. Robust anisotropic diffusion. IEEE Trans Image Process 1998; 7: 421-432.
- Ling J, Bovik AC. Smoothing low-SNR molecular images via anisotropic median-diffusion. IEEE Trans Med Imaging 2002; 21: 377-384.
- Suresh A, Shunmuganathan KL. Feature Fusion Technique for Colour Texture Classification System Based On Gray Level CoOccurrence Matrix. J Comput Sci 2012; 8: 2106-2111.
- Ham B, Min D, Sohn K. Robust scale space filter using second order partial differential equations. IEEE Trans Image Process 2012; 21: 3937-3951.
- Chen X, Tang C, Yan X. Switching degenerate diffusion PDE filter based on impulse like probability for universal noise removal. Int J Electron Commun 2014; 68: 851-857.
- Tian H, Cai H, Lai J. A novel diffusion system for impulse noise removal based on a robust diffusion tensor. Neurocomputing 2014; 133: 222-230.
- Khan NU, Arya KV, Pattanaik M. Edge preservation of impulse noise filtered images by improved anisotropic diffusion. Multimedia Tool Appl 2014; 73: 573-597.
- Veerakumar T, Esakkirajan S, Vennila I. Edge preservation adaptive anisotropic diffusion filter approach for the suppression of impulse noise in images. Int J Electron Commun 2014; 68: 442-452.
- Cho SI, Kang SJ, Kim HS, Kim YH. Dictionary-based anisotropic diffusion for noise reduction. Pattern Recogn Lett 2014; 46: 36-45.
- Marami B, Scherrer B, Afacan O, Erem B, Warfield SK, Gholipour A. Motion-robust diffusion- weighted brain MRI reconstruction through slice-level registration-based motion tracking. IEEE Trans Med Imaging 2016; 35: 2258-2269.
- Babaud J, Witkin AP, Baudin M, Duda RO. Uniqueness of the gaussian kernel for scale-space filtering. IEEE Trans Pattern Anal Mach Intell 1986; 8: 26-33.