Research Article - Biomedical Research (2017) Volume 28, Issue 15
A novel unsupervised automated epileptic seizure detection methodology based on complex networks synchronous state with EEG signals
Zhang Xia1, Xueli Cao2*, Ren Hao2 and Wang Min2
1School of Electrical Engineering, Longdong University, Qingyang City, Gansu Province, PR China
2School of Clinical Medicine, Bengbu Medical College, Bengbu City, Anhui Province, PR China
Accepted on June 7, 2017
Abstract
One of the most challenging tasks with Electroencephalography (EEG) signals is the automated epileptic seizure detection. Traditional automated epileptic seizure detection approaches focus on time or frequency domain to analyse EEG signals. A novel technique for epileptic seizure detection is proposed in this paper, which is based on complex networks synchronous state. The concept of complex network synchronization states has been introduced firstly, and then a network varying with time has been defined by taking the measurement EEG signals as nodes. The dynamic mechanics of the EEG signals network has been quantitatively described by mathematical analysis method. Finally, the mathematical definition, the calculation method and the physical meaning of the EEG signal network synchronous state has been given in this paper. The above theoretical derivation had shown that synchronous state can be employed to assess the level of healthy state with EEG signals. The couple matrix A=(aij)N × N of complex network has been defined by the distance relevance of the measured data, and the left eigenvector (ξ1, ξ2 ,..., ξN), corresponding to the zero feature of the matrix, has been employed to character the local details of complex network nodes. Then, a node fault diagnosis algorithm has been derived based on network synchronous state. The public available EEG database of University of Bonn (UoB), Germany has been used to verify the effectiveness and validity of our proposed method, which has become a benchmark for developing the epilepsy seizure detection systems. Furthermore, the excellent performance of the proposed method has shown that this method can be employed to track the patient healthy state and monitor the moment of epilepsy seizure. This paper has been reported with some references to researchers in related fields.
Keywords
Complex networks, Epileptic seizure detection, EEG signals, Synchronous state.
Introduction
The world health organization illustrated that more than about 1% of the world population suffers from epilepsy, which has been considered as the second largest disease with a little lower than stroke [1]. Even more badly, the spontaneous and unforeseeable occurrence has been its characteristics and challenges. The main changes occur in neurons is the phenomenon of hyper-active and hyper-synchronous neuronal firing [2]. Unfortunately, the patient cannot carry out any self-activities until the exhaustion of their energy during epilepsy seizure, which affects the patients’ life seriously, and the patients’ quality of life can be increasingly hindered by the symptoms [3]. Comprehensive above all, the unsupervised automated epileptic seizure detection method is so important to realize the goal of making the epileptic seizure activity to be considered as a controllable and curable disease.
In the literatures of recent decades, biomedical signal processing area had been developed by extracting relevant feature information directly from raw physiological data sets. And furthermore, the EEG signals have been considered as a non-invasive, low-cost and effective technique to detect the changes of electrical activity [4,5]. However, the common EEG signals, collected from the occurrence of epileptic seizures, always contained non-periodic, non-linear and non-stationary signal, which brings a great challenge to analyse the EEG signals [6]. Over recent decades, automated epileptic seizure detection methodology, aimed at assisting the experts in the time-consuming and tedious process, have been made to develop by many attempts.
The detection of seizures based on EEG signals can be treated as a binary problem, where the goal is to discriminate the ictal and seizure-free states. The most significant of the epileptic seizure detection methodology concentrates in two aspects, called the feature extraction and pattern recognition. In the domain of feature extraction, different approaches have been employed in these systems with varying degrees of success. More recently, frequency domain analysis using fast Fourier transform [7], Hilbert-Huang transform [6], and time-frequency domain methods like dual-tree complex wavelet transforms [8], especially wavelets, such as multiwavelet-based time-varying modeling scheme [9], and the normalized Haar discrete wavelet packet transform [10], researches have often been employed to extract the discriminating features from the complex EEG signals. These features, including entropy [11,12], spectral power [13], energy [14], and so on [15,16], have shown its high level of performance for characterizing slight changes in EEG signals.
Once the feature sets are extracted, pattern recognition approaches are employed to identify the class according to the input features. Various pattern recognition approaches have been reported in recent literatures. These methods, such as neural network [8], extreme learning machine [5], Support Vector Machine (SVM) [2,12], have been made to employ a certain number of features for training and the remaining for testing. The accuracy of the recognition methods depends on two points, i.e. efficient feature extraction and train-to-test ratio [8].
To the best of our knowledge, although many epileptic seizure detection methodologies have been developed, very few of the investigations have so far tested the effect of combining the other theory methods. And the purpose of this paper is to construct a novel unsupervised automated epileptic seizure detection technique for classification of ictal and seizure-free EEG signals. Currently, complex networks have been employed to analyse different time series, such as biomedical and brain signals. Complex network has been considered as a mathematical model with relational information, which can be represented by a graph. And the graph theory provides a method to capture the topology of a network and to extract the main characteristics across networks which can help better understand the relationships between networks [17].
The remainder of this paper is organized as follows. In section 2, the challenges and main problems in epileptic seizure detection, and a case study on the public available EEG database of University of Bonn (UoB), Germany [18,19] to verify the effectiveness and validity of our method, which has become a benchmark for developing the epilepsy seizure detection systems, have been represented and how we considerate it with our method. Section 3 describes the novel unsupervised automatic epileptic seizure detection methodology based on complex networks synchronous state. The experimental results and some discussions have shown the effectiveness of our method for epileptic seizure detection in section 4. Finally, some conclusions and our directions of future research work have been pushed out, and furthermore, the excellence and limitations have also been described in this section.
Challenge and Problem Statement
Currently, epilepsy seizure detection has only visual inspected with EEG recordings by experienced neuro-physiologists or trained neuro-clinicians [20]. This visual inspection on EEG recordings hinders the diagnosis procedure, and furthermore, the EEG recordings acquisition process always lasts several hours or more. Several hours are sufficient to make the patient tired. And unfortunately, the accuracy of the doctors’ diagnosis result is very poor and entirely influenced by the virtue of experience, which is to be born with great arbitrariness. In addition, the EEG signals are more likely to be subjected by the interference from background noise, artifacts and interfering expressions from other neurological symptomatology. For above reasons, some methods for automated detection of epileptic seizures could serve as a fundamental clinical tool for the scrutiny of EEG signals in a more robust, accurate and computationally efficient manner [8]. And furthermore, assessing the healthy state of epilepsy patients from the global perspective and the local perspective can be considered as an expected method.
This study has employed the public available EEG database of University of Bonn (UoB), Germany [20] to verify the effectiveness and validity of our method, which has become a benchmark for developing the epilepsy seizure detection systems. This sample contained five subsets, i.e. A-E respectively, as shown in Table 1. Five healthy volunteers had been invited to make their EEG signals recorded and these signals had been formed as seizure-free signals in A and B sets, which were acquired by using gold plated surface electrodes placed with the principle according to 10-20 international electrode placement system. The five healthy volunteers were relaxed and awake with eyes open (subset-A) and eye closed (subset-B), accordingly. The datasets C and D were recorded during seizure-free inter-ictal trials from electrodes, which had been placed opposite to the epileptogenic zone and within the epileptogenic zone, respectively. The dataset E describes epileptic seizure signals, which had been collected by putting the electrodes in the epileptogenic zone. In general, datasets A and B consist of EEG signals recorded from healthy volunteers, and C-E datasets were acquired from epilepsy patients for pre-surgical diagnosis target intracranial electrodes. Therefore, the database from UoB, consists of EEG signals, can be divided into two segments, i.e., normal and inter-ictal segments, as shown in Table 1.
| Individual information | Five healthy individuals | Five epilepsy patients | |||
|---|---|---|---|---|---|
| Dataset A | Dataset B | Dataset C | Dataset D | Dataset E | |
| State | Awake with eyes open (normal) | Awake with eyes closed (normal) | Seizure free (inter-ictal) | Seizure free (inter-ictal) | Seizure activity (ictal) |
| Electrode type | Surface | Surface | Intracranial | Intracranial | Intracranial |
| Electrode placement | International 10-20 system | International 10-20 system | Opposite to epileptogenic zone | Within epileptogenic zone | Within epileptogenic zone |
| No. of epochs | 100 | 100 | 100 | 100 | 100 |
| Epochs duration | 23.6 s | 23.6 s | 23.6 s | 23.6 s | 23.6 s |
Table 1. The definitions and descriptions for the EEG signals from University of Bonn (UoB), Germany.
Table 1 has pointed that each subset contained 100 EEG segments, each lasting for 23.6 s duration with 4097 samples and sampling rate (Fs) of 173.610 Hz. In previous literature, very few of investigations have considered seven different combinations of the datasets A-E, except the reference [8]. This paper has made the emphasis to stand at unsupervised automatic epilepsy detection methods.
The synchronous state of complex network is mainly due to its highly dissipative coupling characteristics, resulting in the failure of a small number of nodes or edges of the network. And this will trigger redistribution of information flow or energy flow in the network, and therefore these cause the network topology to be changed, which makes the network systems to be unbalanced and triggers the synchronous behavior of the network. Furthermore, these characteristics will lead to some roughly large-scale nodes overload or cascade failures.
Synchronous state has been considered as an objective quantitative evaluation method for synchronous behavior in complex networks. The synchronization state is constrained by the network topology and node dynamics, and it has also been considered as the final state of network control. Simply say, it can be seen as a description of a phenomenon that other nodes have been stimulated according to the agreed strategy due to some failures at a node in the network, and some positive feedback has been developed in other nodes accordingly, such as re-allocation of energy, information and so on. And then the whole network would be resulted in an extreme synchronous behavior with some extreme events, like cascading failure, etc. [21]. It has great significance to optimize the network topology and explore the practical application of the network with some researches on the synchronization state of complex networks.
The ideal of the proposed method in this paper can be descripted as that the topological structure in the network can be employed to reflect the close relationships between the same state nodes and the sparseness between different state nodes, i.e., several sub-networks has been formatted and each sub-network can be seen as a system operational state, and therefore, the epileptic seizure detection problem can be transformed into sub-network detection problem. Different sub-networks will produce different complex network synchronization states [22].
Theory and Methods
The consistency between each node in the complex network is considered as the earliest objective quantitative description of complex network synchronization. And latterly, the synchronization state has been proposed to be calculated by weighted average of the eigenvectors of the coupling matrix. That is to say, the weighted average state and the difference between the nodes will tend to be consistent in the network synchronization. Therefore, the weighted average state can be seen as synchronous state.
Basic theory
Considering the dissipative coupled nonlinear dynamic networks, this can be employed to satisfy all the general complex networks.
The function can be represented as following:
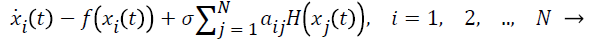 (1)
(1)
Where xi=(xi1, xi2, ..., xin)T Rn is been seen as the solution of the network Equation 1. f C (Rn, Rn), H (Rn, Rn) are the continuously differentiable interconnection functions. Coupling strength can be donated by σ>0. The coupling matrix of the complex network can be calculated by A=(aij)N × N, which can be as an asymmetric matrix (directed network) with meeting the dissipation condition [23].
If the coupling matrix of the complex network A=(aij)N × N satisfies the next two conditions: constructive conditions and matrix rank conditions, then the left eigenvector ξ=(ξ1, ξ2 ,..., ξN)T corresponding to the zero eigenvalue of the coupling matrix A=(aij)N × N is nonnegative, i.e., ξ1 ≥ 0, 1 ≤ i ≤ N. These conditions can be represented as following functions.
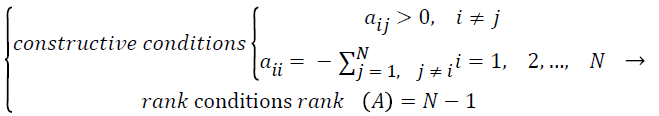 (2)
(2)
Under these circumstances, it can be further assumed that ΣN i=1 ξ1=1, and the weighted average of left eigenvectors of coupling matrix A=(aij)N × N can be calculated as following equation.
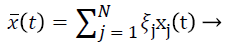 (3)
(3)
Where xi (t) is the solution of coupling system, donated by Equation 1.
The necessary and sufficient condition of complex network is that each node is been tended to be synchronous ͞x (t) when the time t → ∞ and it is not relied on the initial conditions. That is to say, synchronization is the convergence of all nodes at t → ∞ under any given initial conditions. The final synchronization state may be different from different initial conditions, which can be seen as a “curve cluster” without involving in the initial conditions and it can be used as a macro description of the synchronization behavior of complex networks. If the complex network, donated by Equation 1, is under synchronous state, its synchronous state is the set of final set of solutions of Equation 1, which satisfies the positive limit set of the solution of equation.
Assuming that the synchronization manifold of the complex network is donated by Rn × N, and its linear subspace can be represented as M={x=(x1, ..., xN): xi=xj Rn, i, j=1,..., N}. When t → ∞, the solution of Equation 1 xi=(xi1,..., xin) has been convergence to M, the complex network can be considered as synchronization. For all nodes in complex network 1 will be considered to be in synchronization state.
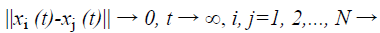 (4)
(4)
Theorem 1. If the complex network is in synchronization state under the condition of Equation 4, i.e. ||xi (t)-xj (t)|| → 0, t → ∞, i, j=1, 2,..., N, the necessary and sufficient condition can be represented as following function.
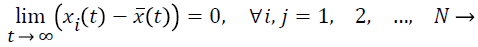 (5)
(5)
Theorem 2. Suppose that f (•) is the linear homogeneous, and if the network is synchronous, the synchronization state ͞x (t) is the solution of the isolated system, i.e.
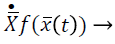 (6)
(6)
Theorem 3. Assume that f (•) satisfies the Lipschitz condition, that is to say, there exists a constant value L>0, which can make the equation ||f (x)-f (y)|| ≤ L ||x-y|| to be held with any given x, y Rn. If the network is in synchronous state, then the synchronization state ͞x (t) will meet the following function.
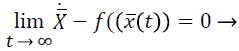 (7)
(7)
These three Theorems have given the relative knowledge of the network synchronous state, for more details, you can refer to [22-25]. Theorem 1 can be employed to prove that the necessary and sufficient condition of complex network is the equation 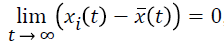 , the expression ͞x (t) can be employed to define the synchronous state, which is calculated as the weighted average states of the nodes. Theorem 2 can be used to prove that if f is the linear homogeneous, then ͞x (t) is the solution of isolated nodes. Theorem 3 can be pushed out to prove that if f is a nonlinear case, only it satisfies the Lipschitz condition, then if the network is under synchronous state, ͞x (t) can be considered as the approximate solution of the solitary nodal equation. That is to say, the solution xi (t) satisfies the solution condition of the coupling system, which can be employed to calculate the ͞x (t) by weighted summation. And furthermore, ͞x (t) can be seen as the synchronous state of isolated nodes under the positive limit set.
, the expression ͞x (t) can be employed to define the synchronous state, which is calculated as the weighted average states of the nodes. Theorem 2 can be used to prove that if f is the linear homogeneous, then ͞x (t) is the solution of isolated nodes. Theorem 3 can be pushed out to prove that if f is a nonlinear case, only it satisfies the Lipschitz condition, then if the network is under synchronous state, ͞x (t) can be considered as the approximate solution of the solitary nodal equation. That is to say, the solution xi (t) satisfies the solution condition of the coupling system, which can be employed to calculate the ͞x (t) by weighted summation. And furthermore, ͞x (t) can be seen as the synchronous state of isolated nodes under the positive limit set.
EEG signal anomaly detection network
The relative knowledge on the synchronous state of complex network can be employed to realize the epileptic seizure detection, and the key point of this process relay on that the network synchronization state does not depend on the initial condition, i.e., the nodes of complex network will have the corresponding network synchronization state solution under any given moment and any given state. This means that when it satisfied this key point and defined a complex network, the coupling matrix defined by the association between nodes needs to meet the constraint of Equation 2. The construction process of the EEG signal anomaly detection network, the mathematical definition, the calculation method and its physical meaning of the network synchronization state has also been pushed out in the following contents.
Assuming that under any time t, with the EEG signal from several sensor nodes, such as the number of N sensors, it can define a network coupling matrix that satisfies Equation 2. The calculation method can be described as following function.
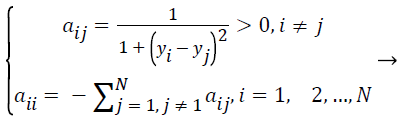 (8)
(8)
The rank of the coupling matrix in the complex network can be proved as rank A=N-1, the synchronization manifold of the nonlinear dissipative coupled nonlinear dynamical network 1 can be considered as the subspace M={x=(x1,..., xN): xi=xj Rn, i, j=1, 2,..., N} in space Rn × N. When t, the solution x=(x1, x2, ..., xN) of the equation converges to M, then the complex network 1 become fully synchronized.
If the complex network 1 is in synchronization state under the Equation 4 condition, i.e., ||xi (t)-x (t)|| → 0, t → ∞, i, j=1, 2, …, N and its sufficient and necessary condition is 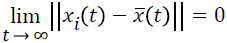 . Therefore, the weighted average state ͞x (t) of the complex network nodes can be seen as the synchronization state of the EEG signal detection network, that is to say, when the network is under synchronization state, each node converges to the weighted average state ͞x (t). The mathematical description can be donated by following function.
. Therefore, the weighted average state ͞x (t) of the complex network nodes can be seen as the synchronization state of the EEG signal detection network, that is to say, when the network is under synchronization state, each node converges to the weighted average state ͞x (t). The mathematical description can be donated by following function. 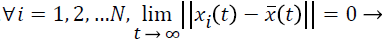 (9)
(9)
It should be noted that the synchronization state of EEG signal detection network can be employed to evaluate the healthy state of the patient’s brain on a macro view. And while the left eigenvectors ξ=(ξ1, ξ2 ,..., ξN), corresponding to the zero eigenvalues of the coupling matrix A=(aij)N × N, can be used to reflect the local details of EEG signal detection network. Therefore, the healthy state of the patient’s brain can be synthetically evaluated by calculating the synchronization state of the EEG signal detection network, and the left eigenvector (ξ1, ξ2 ,..., ξN) can be employed to identify the anomaly of EEG signal to realize the epileptic seizure detection. At this point, the unsupervised automated epileptic seizure detection methodology can be divided into five parts.
Step one, according to the measurement results, the dynamic EEG signals anomaly detection network can be constructed in real-time, and the coupling matrix A=(aij)N × N can also be calculated.
• Step two, calculating the zero eigenvalue of the coupling matrix A=(aij)N × N and then its corresponding left eigenvectors ξ=(ξ1, ξ2 ,..., ξN) can be obtained followed by.
• Step three, the weighted average state ͞x (t) of each node is calculated, i.e., the synchronization state of EEG signal detection network.
• Step four, the state of epilepsy seizures can be judged according to the change of the synchronization state between this time and previous value.
• Step five, if the synchronization state of the EEG signal detection network changes greatly and exceeds the tolerable threshold, the anomaly EEG signal can be found out through backtracking the left eigenvector ξ=(ξ1, ξ2 ,..., ξN).
In this epileptic seizure detection methodology, the actual physical meaning of the coupling matrix A=(aij)N × N is that the distance relative vector between different EEG signals can be employed to reflect the spatial characteristics for the same or similar objects in the anomaly EEG signal detection network. And the left eigenvector corresponding to its zero eigenvalue is a visual representation of the anomaly of the measurement EEG signal of each node in EEG signal detection network. The synchronization behavior of EEG signal detection network describes the degree of network synchronization behavior on the micro view, and the degree of consistency of the whole network evaluates external objects.
Adaptive unsupervised threshold and epileptic seizure detection methodology
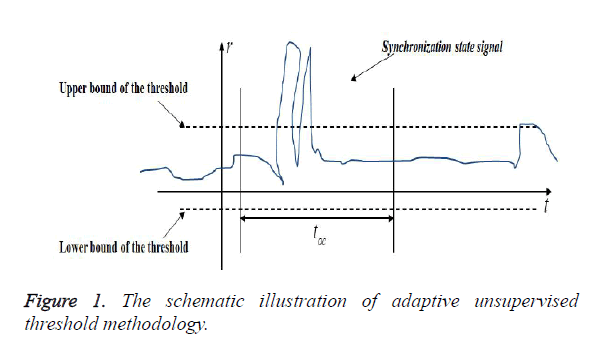
Under these circumstances, a simple way to achieve epilepsy seizure detection is only to set a constant threshold T. Furthermore, the epilepsy can be considered to happen when the amplitude of synchronization state signal of EEG signal detection network is larger than the threshold T, as shown in Figure 1. However, due to long time EEG signal acquisition and measurement and the noise influence from background or other factors, which make the threshold to have adequate tolerance ability to avoid alarms. And furthermore, the EEG recordings process always lasts several hours or more, which makes the patient to be more tired, and the accuracy of the expert’s diagnosis result becomes more and more poor with time going by.
All the above reasons, some methods for automated detection of epileptic seizures should serve as a fundamental clinical tool for the scrutiny of EEG signals in a more robust, accurate and computationally efficient manner [8]. And in addition, the larger the threshold is, the less detection sensitivity is. A balance should be achieved between the false alarm and the detection sensitivity.
The ideal of this threshold methodology lies at the effectiveness under the varied signal disturbance or uncontrolled interference in time sequence. In order to achieve the epilepsy seizure detection, the threshold should be derived from a segment of the epilepsy EEG signal based on statistical principle [26]. In general, the EEG signal can be considered as approximately meet the normal distribution, the mean and variance of the n samples in the segment of the EEG signals can be computed by using following function.
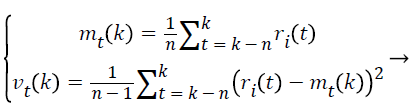 (10)
(10)
Where 0<n<k, ri (t) donates the synchronization state signal.
Generally, due to the non-periodic, non-linear and non-stationary characteristics, different healthy state of patients’ will cause different changes in the EEG signals, which corresponds different levels of changes on EEG signals. And this can be described by the variance vt (k). However, if an incipient change, presented as a slow changing synchronization state signal happened in the EEG anomaly detection network, it is hard to detect the anomaly EEG signal. In our consideration, the decision of the anomaly EEG signals happening is not only depended on the threshold, but also the time with the signal beyond the threshold. Figure 1 presents the schematic illustration of this adaptive unsupervised threshold methodology. And the constant upper bound and lower bound can be donated by Tcu, Tcl, toc represents the tolerate time. When the synchronization state satisfies the rule, represented as r>Tcu or r<Tcl for longer than toc, then the decision of incipient epilepsy disease will be considered to happen.
When an epilepsy disease happen, the dynamic of the brain system changes violently, then it can be represented in a form of violent deviation of EEG signal. However, if the derivation is result from noise or other disturbance, the duration time of the derivation alarm should not be longer than toleration time toc. Furthermore, the threshold would be increased violently due to the abrupt non-stationary changes, which leads to a blind-spot behind the first series of anomaly EEG signal alarms, and this phenomenon, will soon disappear with time going.
Above all, the unsupervised automated epileptic seizure detection methodology can be divided into three parts. Firstly, the complex network is constructed by EEG signals. Secondly, the synchronization state can be calculated by Equations 2, 3 and 8. Finally, a threshold approach is employed to detect the EEG anomaly signal, and this can be used to achieve the epileptic seizure detection.
Experimental Results and Discussion
In this section, we present a case study on the public available EEG database of University of Bonn (UoB), Germany, to demonstrate the effectiveness and reliability of the proposed methodology. Noted that, for the purpose of epilepsy seizure detection, the complex network has been first constructed with EEG signals to form the EEG anomaly signal detection network. Furthermore, different healthy state of patients’ will correspond to different synchronization state of EEG anomaly signal detection network, and the left eigenvector corresponding to its zero eigenvalue is a visual representation of the anomaly of the EEG signal of each node in EEG signal detection network. Consequently, the patient can be considered as a healthy one with smaller amplitude comparing with the appropriately adaptive dynamic threshold, and the duration time of the derivation alarm has been viewed to be longer than toleration time toc, and the patient will be considered to be in epilepsy seizure state.
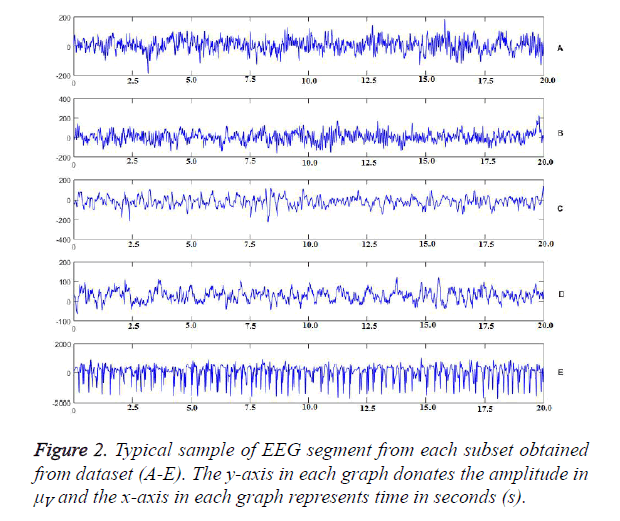
Figure 2 represents the typical sample of EEG segment from each subset in A-E datasets. The y-axis in each graph donates the amplitude in μV and the x-axis in each graph represents time in seconds (s). Obviously, the amplitude of dataset E is very different between others. However, the difference between the other four datasets is quietly small, which cannot be detected out by traditional methodology. Furthermore, the traditional detection methods can only be employed to analyse a single EEG signal, and it cannot be used to detect the relationships between the EEG signals.
The main innovate of this proposed methodology is that epilepsy seizure detection has been developed into the problem that the EEG data samples, reflected the healthy state of patients’, has been divided into different categories, and then the comprehensive synchronization state of complex network, consists of EEG signals, can be calculated to realize the classification of different healthy states, then the epilepsy seizure detection can be achieved finally. In this proposed methodology, the EEG signal sample has been taken as the node, and the relationships between different signals have been considered as the edge to establish the EEG anomaly signal detection network model. Only in this way, the epilepsy seizure detection problem can be transformed into pattern recognition clustering problem. Furthermore, the relationships between different EEG signals can be described into the cognitive domain, which can make the corresponding algorithm considered more complex problems and the model is very intuitive, simple and universal applicability.
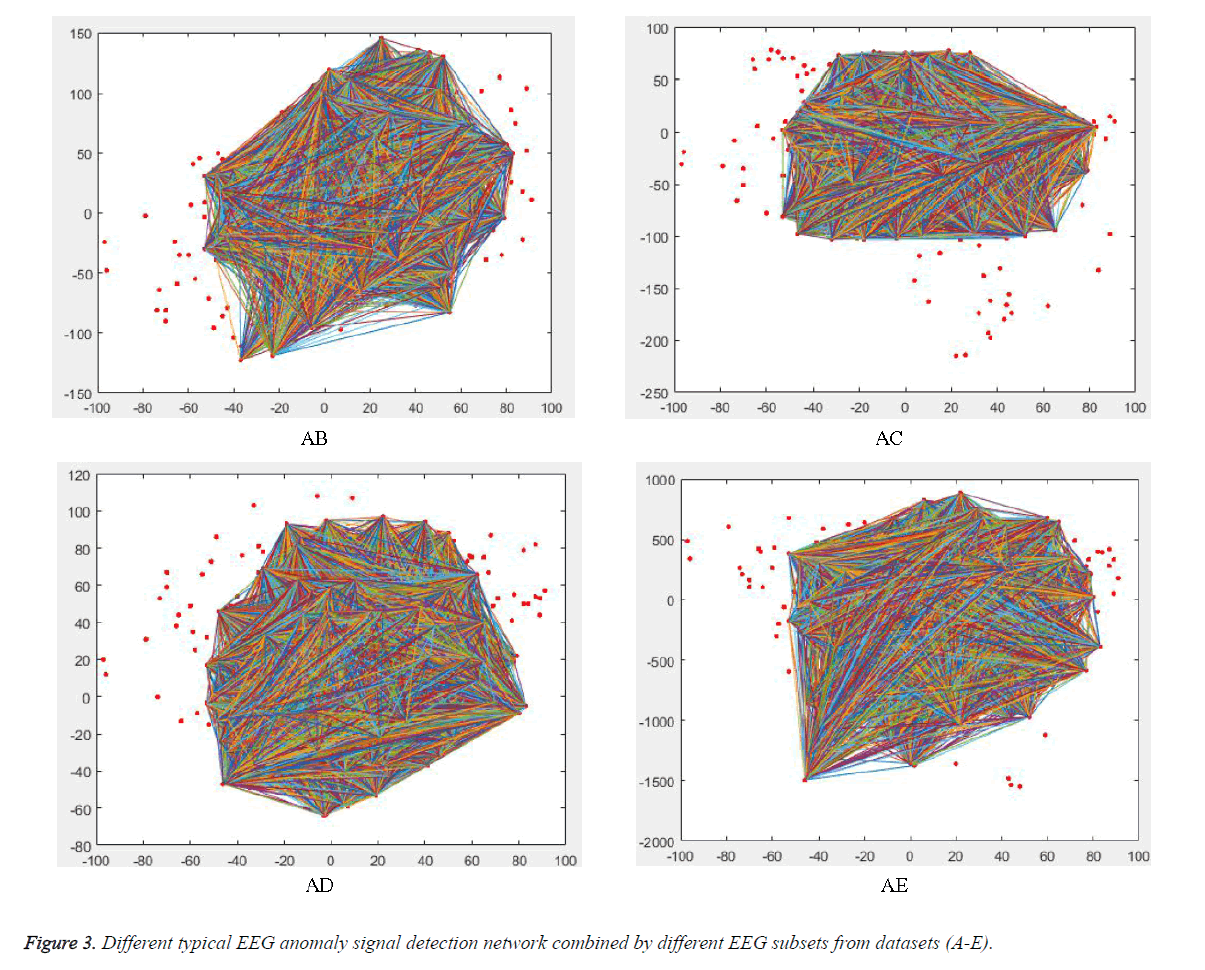
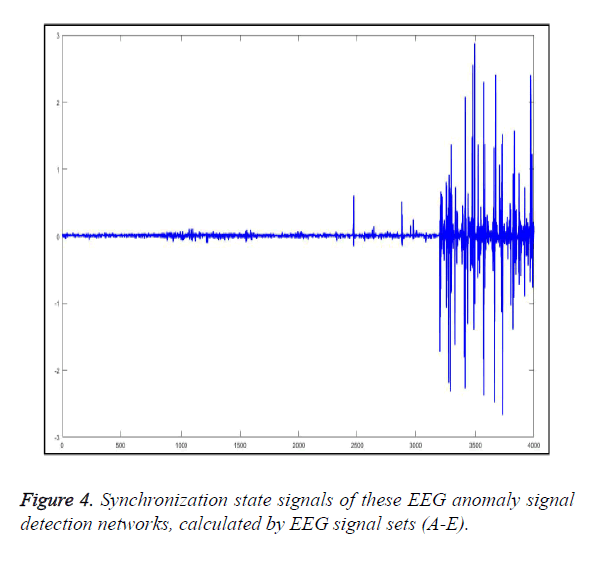
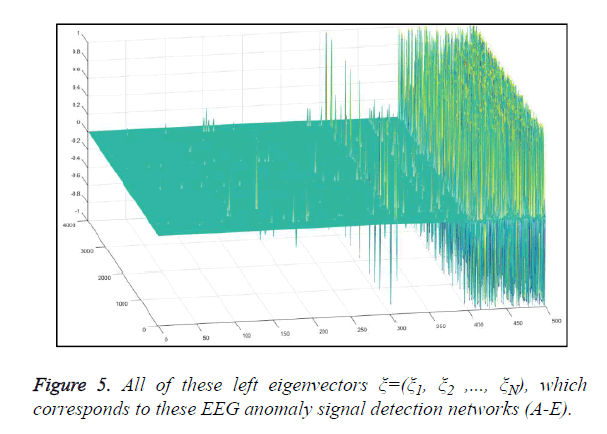
Typical EEG anomaly signal detection network can be seen in Figure 3. From the figure, we can know that different combinations with different EEG signals will correspond to different EEG anomaly signal detection networks, and its topology are completely different. And therefore, the synchronization state signals of these EEG anomaly signal detection networks are also extremely different, as shown in Figure 4. And its corresponding left eigenvectors ξ=(ξ1, ξ2 ,..., ξN) are also like this, as shown in Figure 5.
In this case study, 500 sample points from each EEG subsets (like A-E), and each EEG subset has been employed with only 4000 sample points to realize 8 segments, all of these EEG signal sets can be combined into 4000 groups. During the simulation, the relative variables ͞x (t) have different amplitudes and ranges, and a large difference between their maximum and minimum values often exist. Performing certain preprocessing operations on the inputs and outputs data are more efficient in the training work. The data normalization step is sensitive to the training procedure, and it has been certificated in actual experiment.
Specifically, the following case study is performed on the raw data by the following equation, Xn=2 (X-a)/(b-a) where a, b represents the maximum and minimum ranges of the signal X, respectively, and Xn donates the normalized X.
Figure 4 represents 4000 synchronization state signals of the 4000 segments. From the previous 2400 EEG signal segments, its synchronization states are quite small, which means these EEG signals are from healthy human being or a patient, who are not in the epileptic seizure period. However, the change on variance of middle 800 EEG signal segments is slow, and this means that the D EEG signal is collected from a patient, who is on the verge of imminent epilepsy seizure. Finally, the last 800 synchronization state signals are changing violently, and this tells us that these EEG signals are collected from an epilepsy patient.
Figure 5 represents all of the left eigenvectors ξ=(ξ1, ξ2,..., ξN), which corresponds to the zero features of the couple matrix A=(aij)N × N. The local details of EEG anomaly signal detection network can be described by these left eigenvectors. In Figure 5, every signal consisted by 500 sample points, including 100 sample points from each EEG signal set (A-E). The changes of previous 300 sample points are quite small, while 100 sample points in middle has some variations in glitches. And the last 100 points have violently changed, which are from epilepsy patients.
It should be noted that it is very easy to observe the epilepsy seizure time, as shown in Figures 4 and 5. After the epilepsy seizure happen or before happen, the EEG signal, from the corresponding patients, vibrates violently. And then synchronization state and corresponding left eigenvectors will increase. Above all, the epilepsy seizure can be detected effectively by our novel unsupervised automated epileptic seizure detection methodology and the performance has been certificated and illustrated.
Conclusions, Limitations and Future Work
This paper, a novel methodology is proposed to realize epilepsy seizure detection for potential patients with epilepsy, which is established on the full consideration on building concise and efficient architecture, and this can be employed to achieve the goal on unsupervised automated epilepsy detection. In the light of this framework, the epilepsy seizure detection methodology will have a ability to self-correction and selftraining, which can be employed to provide some approaches to realize the epilepsy seizure detection.
The proposed methodology can be employed to solve one of the most challenging tasks on automated epileptic seizure detection. This paper firstly introduced the concept of synchronization state of complex network, and then an EEG anomaly detection network has been defined by taking the measurement EEG signals. The study on the public available EEG database of University of Bonn (UoB), Germany, had shown that synchronization state can be employed to assess the level of healthy state with EEG signals. And the effectiveness and validity of our proposed method have also been verified by this case study. Furthermore, the excellent performance of the proposed method result has shown that this method can be employed to track the patient healthy state and monitor the moment of epilepsy seizure.
The endeavours in this paper are to develop a comprehensive evaluation on the confusion state of healthy or disease from the original EEG signal. The classification of seizure method is not intended to substitute physicians, but rather to supply them an additional analyzing tool. The excellence and limitations of this paper can be summarized as following sentences. The first one is that this novel automated epileptic seizure detection methodology can be employed as an adaptive and unsupervised feature extraction method. And furthermore, synchronization state is the research result of complex network theory, which can be employed to realize the goal on assess the level of healthy state with EEG signals for epilepsy patients. The advantage lies at that it is possible to analyse the EEG signals both from the global perspective and the local perspective to assess the healthy state of epilepsy patients.
However, how the performance of the proposed model will develop with time going and this will be the first question that we will continue to study. Whether this model is suitable to realize the epilepsy seizure detection for other potential patients is also our consideration and it has become our one research direction and hot topics over the next several decades.
Acknowledgement
This work was supported by the National Natural Science Foundation of China, No.61302116.
References
- Guangyi C. Automatic EEG seizure detection using dual-tree complex wavelet-Fourier features. Exp Sys Appl 2014; 41: 2391-2394.
- Varun J, Ram BP, Antony V. Classification of ictal and seizure-free EEG signals using fractional linear prediction. Biomed Sig Proc Contr 2014; 9: 1-5.
- Mohamed ELM, Abdelghani B, Mohamed S. An automatic mobile-health based approach for EEG epileptic seizures detection. Exp Sys Appl 2015; 42: 7157-7174.
- Yuedong S, Jiaxiang Z. Automatic recognition of epileptic EEG patterns via extreme learning machine and multi-resolution feature extraction. Exp Sys Appl 2013; 40: 5477-5489.
- Alice DL, Rodrigo Z, Andrew JC, Sydney SC. Widespread changes in network activity allow non-invasive detection of mesial temporal lobe seizures. Brain 2016; 1-15.
- Kai F, Jianfeng Q, Yi C, Tao Z. Hilbert marginal spectrum analysis for automatic seizure detection in EEG signals. Biomed Sig Proc Contr 2015; 18: 179-185.
- Hubert C. A time-frequency convolutional neural network for the offline classification of steady-state visual evoked potential responses. Patt Recogn Lett 2011; 32: 1145-1153.
- Piyush S, Tapan KG. A novel robust diagnostic model to detect seizures in electroencephalography. Exp Sys Appl 2016; 56: 116-130.
- Yang L, Mei-Lin L, Ke L. A multiwavelet-based time-varying model identification approach for time-frequency analysis of EEG signals. Neurocomput 2016; 193: 106-114.
- Thiago LT, Alice JK, Cesar RR. Automated drowsiness detection through wavelet packet analysis of a single EEG channel. Exp Sys Appl 2016; 55: 559-565.
- Quan L, Yi FC. A comparison of five different algorithms for EEG signals analysis in artifacts rejection for monitoring depth of anesthesia. Biomed Sig Proc Contr 2016; 25: 24-34.
- Nicoletta N, Julius G. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Exp Sys Appl 2012; 39: 202-209.
- Junhua L, Zbigniew S. Feature learning from incomplete EEG with denoising autoencoder. Neurocomput 2015; 165: 23-31.
- Tapan G, Bijay KP, Sneh A. A comparative study of wavelet families for EEG signal classification. Neurocomput 2011; 74: 3051-3057.
- Yang L, Chong YW, Biao J, Ziwen P. Sparse multivariate autoregressive modeling for mild cognitive impairment classification. Neuroinform 2014; 12: 455-469.
- Yang L, Qing L, Si RT. High-resolution time-frequency analysis of EEG signals using multiscale radial basis functions. Neurocomput 2016; 195: 96-103.
- Mohammed D, Yan L. Complex networks approach for EEG signal sleep stages classification. Exp Sys Appl 2016; 63: 241-248.
- Andrzejak RG, Lehnertz K. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: dependence on recording region and brain state. physical review E. Stat Nonlinear Soft Matt Phys 2001; 64: 061907.
- Ren H, Jianfeng QC. An adaptive unsupervised classification of seizure method based on LMD-MSSE with EEG signals. Biomed Res 2017; 28: 1-8.
- Solomon LM, Emilio P, Philippe R. Epilepsy: new advances. Lancet 2015; 385: 884-898.
- Jun Y, Yufei T, Haibo H, Yan S. Cascading failure analysis with DC power flow model and transient stability analysis. IEEE Trans Power Sys 2015; 30: 285-297.
- An X, Zhang L, Li Y, Zhang J. Synchronization analysis of complex networks with multi-weights and its application in public traffic network. Physica A 2014; 412: 149-156.
- Bo L, Wenlian L, Tianping C. Synchronization in complex networks with stochastically switching coupling structures. IEEE Trans Autom Contr 2012; 57: 754-760.
- Xinsong Y, Jinde C, Jianquan L. Stochastic synchronization of complex networks with non-identical nodes via hybrid adaptive and impulsive control. IEEE Trans Circ Sys I Reg Pap 2012; 59: 371-384.
- Wenwu Y, Pietro D, Guanrong C, Mario B, Jurgen K. Distributed adaptive control of synchronization in complex networks. IEEE Trans Autom Contr 2012; 57: 2153-2158.
- Jian S, Yi C, Chunxiao S. BLDC motor speed control system fault diagnosis based on LGRF neural network and adaptive lifting scheme. Appl Soft Comput 2014; 14: 609-622.