Research Article - Journal of Applied Mathematics and Statistical Applications (2018) Volume 1, Issue 1

Uni-soft hyper BCK-ideals in hyper BCK-algebras.

*Corresponding Author:

Xiao Long Xin
Department of Mathematics, School of Mathematics, Chang-an Campus of Northwest University, Xian 710127, P.R. China.

Accepted date: November 29, 2017

Citation: Xin XL, Zhan J, Jun YB. Uni-soft hyper BCK-ideals in hyper BCK-algebras. J Appl Math Stat App. 2018;1(1):4-9.

Abstract

The soft set theory of the notion of a (weak, strong, reflexive) hyper BCK- ideal is discussed and relations among them are provided. Some related properties are investigated.

Keywords

Uni-soft hyper BCK-ideal, Uni-soft strong hyper BCK-ideal, Uni-soft s-weak hyper BCK-ideal, Uni-soft weak hyper BCK-ideal, Uni-soft reflexive hyper BCK-ideal.

Introduction

Molodtsov introduced the concept of soft set as a new mathematical tool for dealing with uncertainties that is free from the difficulties that have troubled the usual theoretical approaches [1-8]. Molodtsov pointed out several directions for the applications of soft sets. At present, works on the soft set theory are progressing rapidly. Maji et al. [6] described the application of soft set theory to a decision-making problem. Maji et al. [5] also studied several operations on the theory of soft sets. Chen et al. [1] presented a new definition of soft set parametrization reduction, and compared this definition to the related concept of attributes reduction in rough set theory. The algebraic structure of set theories dealing with uncertainties has been studied by some authors. The hyperstructure theory (called also multialgebras) is introduced in 1934 by Marty [7] at the 8th congress of Scandinavian Mathematiciens. Around the 1940’s, several authors worked on hypergroups, especially in France and in the United States, but also in Italy, Rssia and Japan. Over the following decades, many important results appeared, but above all since the 1970’s onwards the most luxuriant flourishing of hyperstructures has been seen. Hyperstructures have many applications to several sectors of both pure and applied sciences. In Jun et al. [4], applied the hyperstructures to BCK-algebras, and introduced the concept of a hyper BCK-algebra which is a generalization of a BCK- algebra, and investigated some related properties. They also introduced the notion of a hyper BCKideal and a weak hyper BCK-ideal, and gave relations between hyper BCK-ideals and weak hyper BCK-ideals. Jun et al. [3] gave a condition for a hyper BCK-algebra to be a BCK-algebra, and introduced the notion of a strong hyper BCK- ideal, a weak hyper BCK-ideal and a reflexive hyper BCK-ideal. They showed that every strong hyper BCK-ideal is a hypersubalgebra, a weak hyper BCK-ideal and a hyper BCK-ideal; and every reflexive hyper BCK-ideal is a strong hyper BCK-ideal. In this paper, we introduce the notions of uni-soft hyper BCK-ideal, uni-soft strong hyper BCK-ideal, uni-soft s-weak hyper BCK-ideal, unisoft weak hyper BCK-ideal, and uni-soft reflexive hyper BCKideal, and investigate several related properties. We provide conditions for a uni-soft weak hyper BCK-ideal to be a uni-soft s-weak hyper BCK-ideal. We consider characterizations of a uni-soft (weak, reflexive) hyper BCK- ideal. We show that the soft union of uni-soft (weak, s-weak, strong) hyper BCK-ideals is also uni-soft (weak, s-weak, strong) hyper BCK-ideal.

Preliminaries

Let H be a nonempty set endowed with a hyper operation “◦”, that is, ◦ is a function from H ×H to p(H) = p(H)\ {φ} . For two subsets

A and B of H, denote by A ◦ B the set ∪{a ob|a∈ A,b∈B} . We shall use x ◦ y instead of x o{y},{x}o y,or{x}o{y}

By a hyper BCK-algebra (see [4]) we mean a nonempty set H endowed with a hyper operation “◦” and a constant 0 satisfying the following axioms:

(H1) (x o z) o ( y o z) « x o y ,

(H2) (x o y) o z = (x o z) o y ,

(H3) x oH«{x},

(H4) x « y and y «x imply x = y ,

for all x, y, z∈H , where x «y is defined by 0∈x o y and for every A, B ⊆ H, A«B

is defined by ∀a∈ A , ∃b ∈ B such that a « b.

In a hyper BCK-algebra H, the condition (H3) is equivalent to the condition:

(a1) x ◦ y « x imply x = y for all x, y ∈ H.

In any hyper BCK-algebra H, the following hold (see [4]):

x o0«{x},0o x «{0},0o0«{0},

(Ao B)oC = (AoC)o B, Ao B«A,0 oA«{0}, (2.2)

0« x, x « x, A«A, Ao B«A, (2.3)

A ⊆ B ⇒ A«B, (2 .4)

0o x = {0},0 o A = {0}, (2 (.5)

A « {0} ⇒ A = {0}, (2.6)

x∈x o 0, (2.7)

For all x, y, z∈H and for all non-empty subsets A, B and C of H.

A non-empty subset A of a hyper BCK-algebra H is called a hyper BCK-ideal of H (see [4]) if it satisfies

0∈ A, (2.8)

(∀x, y∈H)(x o y«A, y∈ A ⇒ x∈ A) , (2.9)

A non-empty subset A of a hyper BCK-algebra H is called a strong hyper BCK-ideal

of H (see [3]) if it satisfies (2.8) and

(∀x, y∈H)((x o y)∩ A/ =∅, y∈ A ⇒ x∈ A) . (2.10)

A hyper BCK-ideal A is said to be reflexive (see [3]) if if x o x ⊆ A for all x∈H

A non-empty subset A of a hyper BCK-algebra H is called a weak hyper BCK-ideal

of H (see [4]) if it satisfies (2.8) and

(∀x, y∈H)((x o y) ⊆ A, y∈ A ⇒ x∈ A) . (2.11) In what follows, let U be an initial universe set and M be a set of parameters. Let

P(U) denotes the power set of U and A, B, C,· · · ⊆ M .

A soft set (F, A) over U (see [8]) is defined to be the set of ordered pairs (F, A) := {(x, F(x)) : x∈M, F(x)∈ P(U)} where F :M → P(U) such that F(x) =∅if x∈/A

For a soft set (F, M) over U and τ ⊆ U, the set

e(F;τ ) = {x∈M | F(x) ⊆τ } is called the τ -exclusive set of (F, M).

For any soft sets (F, M) and (G, M) over U, we define

(F,M) 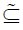(G, M) if F(x) ⊆ G(x) for all x∈M

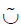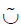The soft union of (F, M) and (G, M), denoted by (F,M) (G, M) is defined to be the soft set over (F G,M) over U in which F 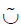G is defined by

(F 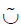G) (x) = F(x) ∪ G(x) for all x ∈ M.

The soft intersection of (F, M) and (G, M), denoted by (F,M) 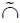(G, M) is defined to be the soft set over U in which F 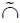G is defined by

(F 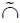G)(x) = F(x)∩G(x) for all x∈M .

In what follows let M denote a hyper BCK-algebra unless otherwise specified. For a soft set (F, M) over U and A ⊆ M , by F(A) and 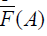we mean

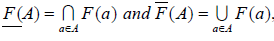respectively.

Definition 3.1.

A soft set (F, M) over U is called a uni-soft hyper BCK-ideal over U if it satisfies:

(∀x, y∈M)(x«y ⇒ F(x) ⊆ F( y)), (3.1)

(∀x, y∈M)(F(x) ⊆ F(xy)∪ F( y)) . 3 (.2)

Combining (2.3) and (3.1), we know that every uni-soft hyper BCK-ideal (F, M) over U satisfies:

Example 3.2: Consider a hyper BCK-algebra M = {0, a, b} with then following Cayley table:

Let (F, M) be a soft set over U = R in which

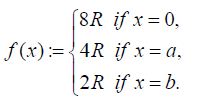
It is easy to check that (F, M) is a uni-soft hyper BCK-ideal over U.

Definition 3.3.

A soft set (F, M) over U is called a uni-soft strong hyper BCKideal

over U if it satisfies:

(∀x, y∈M)(F(x°x) ⊆ F(x) ⊆ F(x°y)∪ F( y)) . 3 . 4 )

Definition 3.4.

A soft set (F, M) over U is called a uni-soft s-weak hyper BCKideal over

U if it satisfies:

(∀x∈M)(F (0) ⊆ F(x)), (3.5)

(∀x, y∈M)(∃a∈ x°y)(F(x) ⊆ F(a)∪ F( y)). (3.6)

Definition 3.5.

A soft set (F, M) over U is called a uni-soft weak hyper BCKideal over

U if it satisfies:

(∀x, y∈M)(F (0) ⊆ F(x) ⊆ F(x°y)∪ F( y)) . (3.7)

Example 3.6: Let M = {0, a, b} be a hyper BCK-algebra which is given in Example

Let (F, M) be a soft set over U = R in which

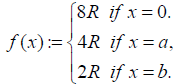
It is easy to check that (F, M) is a uni-soft weak hyper BCKideal over U.

Note that every uni-soft hyper BCK-ideal is a uni-soft weak hyper BCK-ideal. But the converse is not true in general. In fact, the uni-soft weak hyper BCK-ideal (F, M) over U = R in Example 3.6 is not a uni-soft hyper BCK-ideal (F, M) over U = R since

a«b and F(a) < / : F(b).

Theorem 3.7.

Every uni-soft s-weak hyper BCK-ideal is a uni-soft weak hyper BCK- ideal.

Proof: Let (F, M) be a uni-soft s-weak hyper BCK-ideal over U. For any x, y∈M , there exists a∈ x°y such that F(x) ⊆ F(a)∪ F( y) by (3.6). Since F(a) ⊆ F(x°y) , it follows that F(x) ⊆ F(x°y)∪ F( y) . Therefore (F, M) is a uni-soft weak hyper BCK-ideal over U.

It is not easy to find an example of a uni-soft weak hyper BCKideal which is not a uni-soft s-weak hyper BCK-ideal. But we have the following theorem.

Theorem 3.8.

Let (F, M) be a uni-soft weak hyper BCK-ideal over U such that

(∀T ⊆ M)(∃x0 ∈T)(F(x0 ) = F(T)) . (3.8)

Then (F, M) is a uni-soft s-weak hyper BCK-ideal over U.

Proof: By the condition (3.8), we know that for every x, y∈M there exists a₀∈ x^°y such that F(a₀ ) = F(x^°y). It follows from (3.7) that

(∀x, y∈M)(x«y ⇒ F(x) ⊆ F( y)).

Therefore (F, M) is a uni-soft s-weak hyper BCK-ideal over U.

Since every soft set (F, M) over U satisfies the condition (3.8) in a finite hyper BCK- algebra M, we have the following corollary.

Corollary 3.9.

In a finite hyper BCK-algebra M, every uni-soft weak hyper BCK-ideal is a uni-soft s-weak hyper BCK-ideal.

Combining Theorem 3.7 and Corollary 3.9, we know that the concept of uni-soft weak hyper BCK-ideals and uni-soft s-weak hyper BCK-ideals coincide in a finite hyper BCK-algebra.

Proposition 3.10.

Every uni-soft strong hyper BCK-ideal (F, M) over U satisfies the following conditions:

(1) (∀x∈M)(F (0) ⊆ F(x)).

(2) (∀x, y∈M)(x«y ⇒ F(x) ⊆ F( y)).

(3) (∀x, y∈ M)(a∈ x°y ⇒F(x) ⊆ F(a)∪ F( y)).

Proof: (1) Since 0∈ x°x for all x∈M , we have

.

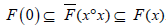Let x, y∈M be such that x«y . Then 0 ∈ x°y , and thus

F(x°y) ⊆ F (0) . It follows from (3.4) and (1) that

F(x) ⊆ F(x°y)∪ F( y) ⊆ F (0)∪ F( y) = F( y).

Let x, y∈M . If a∈ x°y, then F(x°y) ⊆ F(a).Hence

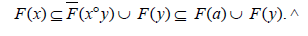
This completes the proof.

Corollary 3.11.

If (F, M) is a uni-soft strong hyper BCK-ideal over U, then^

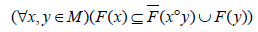(3.9)

Proof. Since 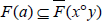for all a∈ x°y , the result follows from Proposition 3.10(3).

Corollary 3.12.

Every uni-soft strong hyper BCK-ideal is both a uni-soft s-weak hyper BCK-ideal (and hence a uni-soft weak hyper BCK-ideal) and a uni-soft hyper BCK- ideal.

Proof: Straightforward.

The following example shows that a uni-soft weak hyper BCKideal may not be a uni-soft strong hyper BCK-ideal.

Example 3.13: Let M = {0, a, b} be a hyper BCK-algebra in Example 3.2. Let (F, M) be a soft set over U = R in which

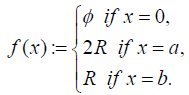
It is easy to check that (F, M) is a uni-soft weak hyper BCKideal over U = R. Since

F(b°a)∪ F(a) = 2R−; /R = F(b),

(F, M) is not a uni-soft strong hyper BCK-ideal over U = R.

Proposition 3.14.

If a uni-soft hyper BCK-ideal (F, M) over U satisfies the condition (3.8), then

(∀x, y∈M)(∃a∈ x°y)(F(x) ⊆ F(a)∪ F( y)). (3.10)

Proof: By the condition (3.8), we know that for every x, y∈M there exists a₀ ∈ x °y

such that F(a₀) = F(x°y) . Hence

F(x) ⊆ F(x°y)∪ F( y) = F(a₀)∪ F( y) by (3.2).

Corollary 3.15.

In a finite hyper BCK-algebra, every uni-soft hyper BCK-ideal (F, M)

over U satisfies the condition (3.10).

Corollary 3.16.

Every uni-soft hyper BCK-ideal is a uni-soft weak hyper BCKideal. Moreover, if M is finite, then every uni-soft hyper BCKideal (F, M) over U is a uni-soft s-weak hyper BCK-ideal over U.

Proof: Straightforward.

Consider the hyper BCK-algebra M = {0, a, b} which is given in Example 3.2. Let (F, M) be a soft set over U = {1, 2, 3, 4, 5} in which

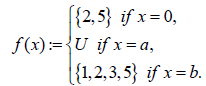
Then (F, M) is a uni-soft weak hyper BCK-ideal over U, but it is not a uni-soft hyper BCK-ideal over U since a«b and F(a)cJF(b).

Lemma 3.17 ([2]): Let A be a subset of a hyper BCK-algebra M. If I is a hyper BCK- ideal of M such that A«I , then A is contained in I.

Theorem 3.18.

For a soft set (F, M) over U, the following are equivalent. (F, M) is a uni-soft hyper BCK-ideal over U.

The τ -exclusive set e(F;τ ) is a hyper BCK-ideal of M for all τ ∈P(U) with e(F;τ )/ = Ø,

Proof: Assume that (F, M) is a uni-soft hyper BCK-ideal over U. Let τ ∈P(U) be such that e(F;τ )/ = Ø. Then F(a) ⊆τ for some a∈ M . By (3.3), F (0) ⊆ F(a) ⊆τ and so 0∈e(F;τ ) . Let x, y∈M be such that x°y«e(F;τ ) and y∈e(F;τ ) . Then for every a∈x o y , there exists a∈e(F;τ ) such that a₀ « a and so F(a) ⊆ F(a₀) by (3.1). Hence

F(a) ⊆τ for all a∈x o y . It follows that F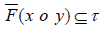and so that

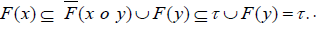
Hence x∈e(F;τ ) and e(F;τ ) is a hyper BCK-ideal of M.

Conversely, suppose the second condition is valid. Let x, y ∈ M be such that x « y and τ = F( y) . Then y∈ e;(F τ ) , and so x∈e(F;τ ) . It follows from Lemma 3.17 that x∈e(F;τ ) and so that F(x) ⊆τ = F( y) . Moreover, let x, y∈M and put τ := F(x o y)∪F( y) . Then y∈e(F;τ ) , and for each a∈x o y we have

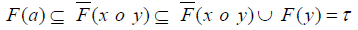
and hence a∈x o y , which implies that x o y ⊆ e(F;τ ) . Thus x o y « e(F;τ ) b y (2.4). Combining y∈e(F;τ ) and e(F;τ ) being a hyper BCK-ideal of M, we obtain x∈e(F;τ ) and so F(x) ⊆τ = F(x o y)∪F( y) . Therefore (F, M) is a uni-soft hyper BCK-ideal over U.

Theorem 3.19

For a soft set (F, M) over U, the following are equivalent.

(1) (F, M) is a uni-soft weak hyper BCK-ideal over U.

(2) The τ -exclusive set e(F;τ ) is a weak hyper BCKideal of M for all τ ∈ P(U) with

e(F;τ )/ =Ø

Proof: The proof is similar to the proof of Theorem 3.18.

Theorem 3.20

If (F, M) is a uni-soft strong hyper BCK-ideal over U, then the τ - exclusive set e(F;τ ) is a strong hyper BCK-ideal of M for all τ ∈P(U) with e(F;τ )/ =Ø

Proof. Let τ ∈P(U) be such that e (F;τ )/ =Ø.Then there exists a∈ e;(F τ ) , and so F(a) ⊆τ . It follows from Proposition 3.10(1)

that F (0) ⊆ F(a) ⊆τ and so that

0∈e(F;τ ) . Let x, y∈M be such that y∈e(F;τ ) and (x o y)∩e(F;τ )/ =Ø. Then there exists a₀∈(x o y)∩e(F;τ ) and hence F(a₀) ⊆τ . Using (3.4), we have

F(x) ⊆ F(x o y)∪ F( y) ⊆ F(a )∪ F( y) ⊆τ ,

which implies that x∈e(F;τ ) . Therefore e(F;τ ) is a strong hyper BCK-ideal of M.

Now we consider the converse of Theorem 3.20.

Theorem 3.21

Let (F, M) be a soft set over U such that

(∀K ⊆ M)(∃a₀ ∈K)(F(a₀) = F(K)) . (3.11)

If the τ -exclusive set e(F; τ) is a strong hyper BCK-ideal of M for all τ ∈ P(U) with

e(F;τ )/ =Ø then (F, M) is a uni-soft strong hyper BCK-ideal over U.

Proof. Assume that e(F;β ) is a strong hyper BCK-ideal of M for all τ ∈ P(U) with e(F;τ )/ =Ø Then there exists x∈e(F;τ ) and hence x o x « x∈e(F;τ ) . Using Lemma 3.17, we have x o x ⊆ e(F;τ ) Thus for each a∈x o x , we have a∈e(F;τ ) and so F(a) ⊆τ . It follows that F(x o x) ⊆ F(x) . Moreover let x, y∈M and put β := F(x o y)∪F( y) . By hypothesis, e(F;β ) is a strong hyper BCK-ideal of M. The condition (3.11) implies that there exists a₀∈(x o y)∩e(F;β ) such that F(a₀) = F(x o y) . Thus and so a₀ ∈ e(F;β ) This shows that a₀∈(x o y)∩e(F;β ) and thus (x o y)∩e(F;β )/ =Ø. Combining y∈e(F;β ) and noticing that e(F;β ) is a strong hyper BCK-ideal of M, we get x∈e(F;β ) . Hence F(x) ⊆ β = F(x o y)∪F( y) . Therefore (F, M) is a uni-soft strong hyper BCK-ideal over U. Since every finite hyper BCK-algebra M satisfies the condition (3.11), we have the following corollary.

Corollary 3.22

Let (F, M) be a soft set over U in a finite hyper BCK-algebra M. If the τ -exclusive set e(F;τ ) is a strong hyper BCK-ideal of M for all τ ∈P(U) with e(F;τ )/ =Ø then (F, M) is a uni-soft strong hyper BCK-ideal over U.

The following example illustrates Theorem 3.21.

Example 3.23: Consider a hyper BCK-algebra M = {0, a, b} with thew following Cayley table:

Let (F, M) be a soft set over U = {1, 2, 3, 4, 5} in which

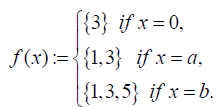
Then

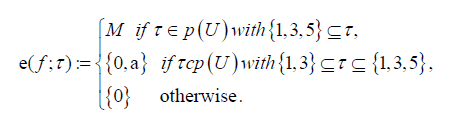
Note that {0}, {0, a} and M are strong hyper BCK-ideals of M. Hence, by Theorem 3.21, (F, M) is a uni-soft strong hyper BCK-ideal over U.

Lemma 3.24: If (F, M) and (G, M) are soft sets over U, then

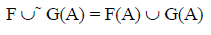
For all A ⊆ M.

Proof: For any subset A of M, we have

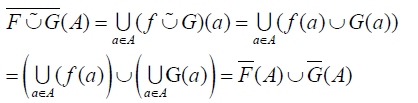
This completes the proof.

Theorem 3.25

The soft union of two uni-soft hyper BCK-ideals is also a unisoft hyper BCK-ideal.

Proof: Let (F, M) and (G, M) be uni-soft hyper BCK-ideals over U. Let x, y ∈ M be such that x « y. Then F(x) ⊆ F(y) and G(x) ⊆ G(y). Hence

(F ∪˜ G) (x) = F(x) ∪ G(x) ⊆ F(y) ∪ G(y) = (F ∪˜ G) (y)

Let x, y ∈ M. Using Lemma 3.24, we have

(F ∪˜ G) (x) = F(x) ∪ G(x) ⊆ (F(x ◦ y) ∪ F(y)) ∪ (G(x ◦ y) ∪ G(y))

= F ∪˜ G(x ◦ y) ∪ (F ∪˜ G) (y).

Hence (F, M) ∪˜ (G, M) is a uni-soft hyper BCK-ideal over U.

By the similar method to the proof of Theorem 3.25, we have the following result.

Theorem 3.26

The soft union of two uni-soft strong (resp. uni-soft s-weak and uni- soft weak) hyper BCK-ideals is also a uni-soft strong (resp. uni-soft s-weak and uni-soft weak) hyper BCK-ideal.

Definition 3.27

A soft set (F, M) over U is called a uni-soft reflexive hyper BCK-ideal

over U if it satisfies:

(∀x, y∈M) F(x o x) ⊆ F( y) , (3.12)

(∀x, y∈M)(F(x) ⊆ F(x o y)∪F( y)) . (3.13)

Theorem 3.28

Every uni-soft reflexive hyper BCK-ideal is a uni-soft strong hyper BCK-ideal.

Proof: Straightforward.

Theorem 3.29

If (F, M) is a uni-soft reflexive hyper BCK-ideal over U, then the τ - exclusive set e(F; τ) is a reflexive hyper BCK-ideal of M for all τ ∈P(U) with e(F;τ )/ =Ø.

Proof: Assume that (F, M) is a uni-soft reflexive hyper BCKideal over U. Then (F, M) is a uni-soft strong hyper BCK-ideal over U, and so it is a uni-soft hyper BCK-ideal over U. Let τ ∈P(U) be such that e(F;τ )/ =Ø. Then F(a) ⊆τ for some a∈ M,and e(F;τ ) is a hyper BCK-ideal of M by Theorem 3.18. Now let x∈M The condition (3.12) implies that F(c) ⊆ F(x o x) ⊆ F(a) ⊆τ for all c∈x o x . Hence c∈e(F;τ ) , and so x o x ⊆ e(F;τ ) . Therefore e(F;τ ) is a reflexive hyper BCK-ideal of M.

Lemma 3.30 ([3]). Every reflexive hyper BCK-ideal is a strong hyper BCK-ideal.

We consider the converse of Theorem 3.29.

Theorem 3.31

For a soft set (F, M) over U satisfying the condition (3.11), if the τ - exclusive set e(F;τ ) is a reflexive hyper BCK-ideal of M for all τ ∈P(U) with e(F;M)/ =Ø then (F, M) is a unisoft reflexive hyper BCK-ideal over U.

Proof. Suppose that e(F;τ ) is a reflexive hyper BCK-ideal of M for all τ ∈P(U) with e(F;M)/ =Ø. Then e(F;τ ) is a strong hyper BCK-ideal of M by

Lemma 3.30: It follows from Theorem 3.21 that (F, M) is a unisoft strong hyper BCK-ideal over U. Thus the condition (3.13) is valid. Let x, y∈M and F( y) = β . Then e(F;β ) is a reflexive hyper BCK-ideal of M, and so x o x ⊆ e(F;β ) . Thus for each c∈x o x , we have c∈e(F;β ) and so F(c) ⊆ β . This shows that F(x o x) ⊆ β = F( y) . Therefore (F, M) is a uni-soft reflexive hyper BCK-ideal over U.

We provide conditions for a uni-soft strong hyper BCK-ideal to be a uni-soft reflexive hyper BCK-ideal.

Theorem 3.32

Let (F, M) be a uni-soft strong hyper BCK-ideal over U satisfying the condition (3.11). Then (F, M) is a uni-soft reflexive hyper BCK-ideal over U if and only if the following assertion is valid.

(∀x∈M)F(x o x) ⊆ F (0) . (3.14)

Proof: Assume that (F, M) is a uni-soft reflexive hyper BCK-ideal over U. The condition (3.12) induces F(x o x) ⊆ F (0) for all x∈M .

Conversely, suppose that the condition (3.14) is valid. Note that (F, M) is a uni-soft hyper BCK-ideal over U. Hence F (0) ⊆ F( y) for all y∈M , which implies from (3.14) that F(x o x) ⊆ F (0) ⊆ F( y) f or all x, y∈M .

Put τ := F(x o y)∪F( y) f,or x y∈M . Then e(F;τ ) is a strong hyper BCK-ideal of M by Theorem 3.20.

Theorem 3.20

The condition (3.11) implies that there exists a₀ ∈x o y such that F(a₀) = F(x o y) , and so F(a₀) ⊆τ . Thus a₀∈e(F;τ ) , which implies that (x o y)∩e(F;τ )/ =Ø Since y∈e(F;τ ) , it follows that x∈e(F;τ ) and so that F(x) ⊆τ = F(x o y)∪F( y) for all x, y∈M Therefore (F, M) is a uni-soft reflexive hyper BCK-ideal over U.

References

1. Molodtsov D. Soft set theory - First results. Comput Math Appl. 1999;19-31.
2. Maji PK, Roy AR, Biswas R. An application of soft sets in a decision-making problem. Comput Math Appl. 2002;1077-83.
3. Maji PK, Biswas R, Roy AR. Soft set theory. Comput Math Appl 2003;555-62.
4. Chen D, Tsang ECC, Yeung DS. The parametrization reduction of soft sets and its applications. Comput Math Appl. 2005;757-63.
5. Marty F. Sur une generalization de la notion de group, 8th Congress Math. Scandinaves, Stockholm 1934;45-9.
6. Jun YB, Xin L. Scalar elements and hyperatoms of hyper BCK-algebras. Scientiae Mathematicae 1999;303-9.
7.  Jun YB, Xin XL, Roh EH. Strong hyper BCK-ideals of hyper BCK-algebras. Math Japon. 2000;493-98.
8.  Jun YB, Zahedi MM, Xin XL. On hyper BCK-algebras. Italian J Pure Appl Math 2000;127-36.