Research Article - Biomedical Research (2018) Volume 29, Issue 13
The impact of imputation procedures with machine learning methods on the performance of classifiers: An application to coronary artery disease data including missing values
Jale Bektaş1*, Turgay Ibrikçi2 and İsmail Türkay Özcan3
1School of Applied Technology and Management, Computer Technology and Information Systems, Mersin University, Erdemli, Mersin, Turkey
2Department of Electrical-Electronics Engineering, Cukurova University, Adana, Turkey
3Department of Cardiology, Mersin University Hospital, Mersin, Turkey
- *Corresponding Author:
- Jale Bektaş
School of Applied Technology and Management
Computer Technology and Information Systems
Mersin University
Erdemli, Mersin, Turkey
Accepted date: June 07, 2018
DOI: 10.4066/biomedicalresearch.29-18-199
Visit for more related articles at Biomedical ResearchAbstract
Prediction and learning in the presence of missing data are pervasive problems in data analysis by machine learning. This study focuses on the problems of collaborative classification with missing data on Coronary Artery Disease (CAD) and suggests alternative imputation methods in the case of the lack of laboratory test as well other specific parameters. This study develops three novel data imputation methods utilizing machine learning algorithms (K-means, Multilayer Perceptron (MLP), and Self- Organizing Maps (SOMs)) and compares the performance of our methods with well-known mean method. Benchmark classification methods (Logistic Model Trees (LMT), MLP, Random Forest (RF), and Support Vector Machine (SVM)) are used to conduct experiments on CAD dataset after imputation. The performance of the classifiers is evaluated according to the values of accuracy, specificity, sensitivity, f-measure, precision and normalized root mean square error. Based on statistical analysis, the SOM imputation method achieves the best values for accuracy (88.23%), F-measure (0.879), and precision (0.881). Moreover, MLP is mostly more stable than other imputation methods when the mean scores of the results of classifiers are considered. According to the results, the data imputation experiments conducted in this study suggests that machine learning imputation methods increase the prediction performance of the classifiers and strengthen disease-diagnosed success.
Keywords
Missing value, Self-organizing maps, Multilayer perceptron, K-means, Coronary artery disease, Classification methods
Introduction
Acute chest pain is one of the frequent causes of presentation to emergency department; however, only 15-20% these presentations of chest pain really have [1]. In addition, it becomes difficult to diagnose the ones which do not have specific symptoms or electrocardiographic signs. Furthermore, there are many factors which cause higher risk for CAD and can be classified according to the National Cholesterol Education Program (NCEP) ATP III Guidelines.
Hospital Information Systems (HISs) are used to collect and provide health information for decision-making and research in hospitals. Studies conducted in the medical field suggest that datasets are formed manually in some cases while they are formed through retrieval from HISs in others [2]. In the records of datasets formed by manual data entry in clinical studies, there is a striking amount of missing values (MVs). Therefore, it is very important to impute MVs for application to medical datasets, and this is an indispensable component of the preprocessing stage in classification problems [3].
The imputation method is one of the tools used to solve MV problems in medical data analysis, and its application depends on the distribution of MVs in the data. The mean/mode imputation method is an example of transforming MVs into new continuous and categorical values depending on the distribution of their features. Recently, fuzzy unordered rule induction algorithm imputation and machine learning have been used as alternative MV imputation methods for many clinical datasets and others with MVs [4-6]. In the literature, machine learning methods have better performances when compared to traditional methods. The methods used in the studies of MV imputation with machine learning in many different domains are Multilayer Perceptron (MLP) [7], Self- Organizing Maps (SOMs) [8,9], Decision Tree (DT) [10] and K-Nearest Neighbors (KNN) [5]. Furthermore, not all algorithms are suitable for all MV problems; hence, it is necessary to choose a suitable method depending on the nature of the study and the structure of the dataset.
This study aims to make more stable diagnosis predictions on the CAD dataset after imputation procedures, and the imputation of MV problem has been examined with the machine learning approach as an alternative to the traditional mean method.
Material and Methods
Description of cardiovascular dataset
This study included 459 patients who presented to the department of cardiology of Mersin Research and Training Hospital, Mersin, Turkey with the suspect of CAD. Angiography is applied as a standard procedure to determine the stenosis. After angiography has been used to determine the location of the lesion, disease of the left main coronary artery (stenosis diameter>50% of vessel diameter) is considered to indicate the presence of CAD. The present study categorizes 22 clinical comorbidities, cardiac status, medical history features into categorical-type and continuous-type format shown in Table 1.
| Feature label | Variable type | Missingness (%) |
|---|---|---|
| Age (Individual's age) | Quantitative/numeric | - |
| Gender (Individual's gender) | Qualitative/categorical | - |
| DM (Diabetes mellitus) | Qualitative/categorical | - |
| FH (Family history) | Qualitative/categorical | - |
| HTN (Hypertension) | Qualitative/categorical | - |
| Smoke | Qualitative/categorical | - |
| Hyp (Hyperlipidemia) | Qualitative/categorical | - |
| LDL (Low-Density Lip.) (mg/dl) | Quantitative/numeric | 13.07 |
| HLD (High-Density Lip.) (mg/dl) | Quantitative/numeric | 12.41 |
| TG (Triglyceride) (mg/dl) | Quantitative/numeric | 12.41 |
| TC (Total Cholesterol) (mg/dl) | Quantitative/numeric | 13.72 |
| Urea (mg/dl) | Quantitative/numeric | 16.78 |
| Hb (Hemoglobin) (g/dl) | Quantitative/numeric | 1.08 |
| Cr (Creatine) (mg/dl) | Quantitative/numeric | 0.6 |
| RDW (Red cell distribution) (mg) | Quantitative/numeric | 3.7 |
| MCV (Mean corpus. volume) (mg) | Quantitative/numeric | 3.7 |
| EF (Electrocardiographic result) (%) | Quantitative/numeric | 18 |
| FBS (Fasting blood sugar) (mg/dl) | Quantitative/numeric | 5.22 |
| Asthma | Qualitative/categorical | - |
| Renal failure | Qualitative/categorical | - |
| COPD | Qualitative/categorical | - |
Table 1. Clinical characteristics relevant to diagnosis missingness percentages are shown for numeric features which have MVs.
The cardiovascular dataset has 314 cases of CAD and 145 cases without CAD with 22 features for each case. Of the total number of cases in the dataset, 277 are completed with all the features and 182 have at least one MV. The complete part of the dataset consists of 210 CAD and 67 without CAD samples. We observed that 182 out of 459 cases have 4.8% to 33.3% MVs in their features. The CAD dataset contains 11 continuous-type of features which has MV at random dropouts.
Imputation techniques
The dataset is separated into two subsets, where the first subset (referred to as set 1) consists of cases that do not include MVs and the second subset (referred to as set 2) has cases that include MVs. The cases in set 2 are listed in ascending order depending on their numbers of MV features. The k-fold cross validation was used in this work to ensure that all data points are used for both training and validation. There are some of the notations as shown in Table 2 placed in imputation algorithms.
| Symbol | Description |
|---|---|
| Nx | MVs sample |
| M1 | Complete part of the CAD dataset (set 1) |
| M2 | The part of the CAD dataset has MVs (set 2) |
| Ci | The ith cluster |
| ci | The centroid of cluster Ci |
| T | Target vector |
| W | Wight vector of BMN |
| Ѳ | Restraint due to the distance of BMN |
Table 2. Table of notations.
K-means imputation process
The K-means cluster method partitions the n samples into k ≤ n sets S=(S1, S2, …, Sk) so as to minimize the variance of the within-cluster sum of squares [11]. The number of clusters is assigned considering the similarity between the cluster centres. For set 1, the number of clusters k is chosen as 6. The algorithm used to carry out the MV imputation method by using the K-means is as follows.
Imputation algorithm 1:
01: Input
02: m1, m2
03: Output
04: m1
05: Begin
06: For i=1 to row no in m2
07: Evaluate feature index Fx=find (empty (Nxi)
08: Fy=~Fx
09: Evaluate Ci, ci of the m1 by K-means
10: Index=0
11: For j=1 to column no of Fx
12: mindist=0
13: For k=1 to 6
14: distk = ||Fyi-Ci||
15: if mindistk>distk then
16: mindistk=distk
17: Index=k;
18: End if
19: Next k
20: Impute Fx with mean values of Cindex
21: Next j
22: m1=m1+(Fxi+Fyi)
23: Next i
24: End
Multilayer perception imputation process
MLP is an artificial neural network in which the hidden layers and neurons in the network topology are determined by a trial and error strategy [12]. An MLP network can undergo a learning process so as to predict MVs. In the MLP imputation process, network consists of one hidden layer and two-layered weight values. The weights of the first layer are related with variables of the input data, and the weights of the second layer are related with the output unit. Features comprising MVs in the training process are used as output while the remaining features are used as input [9]. Training takes place using the complete data, and features including incomplete data are presented to the model for prediction. All features including MVs are presented to the algorithm [13].
Imputation algorithm 2:
01: Input
02: m1, m2
03: Output
04: m2
05: Begin
06: Evaluate feature index Fx=find (empty (m2)
07: Set parameters (train_ratio=70/100, Val_ratio=15/100, Test_ratio=15/100)
08: For i=1 to col no of Fx
09: Ti=m1i;
10: m1=m1-Ti
11: Train MLP network by Ti, m1
12: Ini=m2-Fxi
13: Fxi=Test MLP network by Ini
14: m2=m2+Fxi
15: Next i
16: End
Self-organizing map imputation process
An SOM is a neural network model comprising an input space and an output layer, and its topology is described on a map. Input values in the training set are described as n-dimensional X=(X1, X2, X3… Xn). The weight vector of each node in the output layer is n-dimensional and is described as W=(W1, W2, W3 ….Wn). The node is described as the Best Matching Node (BMN) to calculate the minimum distance. In the course of MVs prediction, it is observed that the size of the map affects the result. In order to eliminate limit restrictions, a square map that can be created based on the shape is used [14]. 8 × 8 SOM network is selected by testing maps of various dimensions ranging between 4 × 4 and 20 × 20. While dimensions smaller than 8 × 8 do not present the data distribution satisfactorily, larger models are observed to fit the training data.
The cases including MVs are given to the SOM network in turn for prediction. When the value of a feature in an incomplete case is presented to the network for prediction, input values comprising MVs are ignored for the selection of the BMN if they already exist in the case. The steps of the MV imputation algorithm are as follows.
Imputation algorithm 3:
01: Input
02: m1, m2
03: Output
04: m1
05: Begin
06: For i=1 to row no in m2
07: Evaluate feature index Fx=find (empty (Nxi))
08: Set parameters
09: epochs=1000
10: Perform Fcn=SSE
11: mapdim=8 × 8
12: Evaluate trainCi, testCi
13: For j=1 to col no of testCi
14: For all wij ɛ W dij=||Nxi-wij||
15: Evaluate weight values of activation group of BMU
16: W (t+1)=W (t)+Ѳ (t) (Dij (t)-W (t))
17: Impute Nxij with mean values of W (t+1)
18: Next j
19: m1=m1+Nxi
20: Next i
21: End
Building the classifiers
Classification algorithms are one of the key points which have the ability to provide correct information for the evaluation to any algorithm within a machine learning framework. From this point of view, in this study classification algorithms are utilized to judge on how well the resultant dataset is classified. Support Vector Machine (SVM) [15], MLP [16,17], RF [18], and LMT [19] are used to evaluate performances due to successful applications in medical data in recent years. All of the input parameters of classifiers are given as Weka default parameters.
Results
The results are evaluated for accuracy (ACC), specificity (Spec), F-measure, and precision (Prec), sensitivity (Sen) in terms of certain metrics. Moreover, the MVs-deleted dataset condition was used as a baseline and the classification performance on datasets obtained as a result of imputation methods is presented in Table 3.
| ACC | Sen | Spec | Fmeas | Prec | ||
|---|---|---|---|---|---|---|
| Mean imputation | SVM | 81.69 | 0.82 | 0.17 | 0.81 | 0.81 |
| RF | 86.92 | 0.86 | 0.09 | 0.875 | 0.877 | |
| MLP | 87.58 | 0.88 | 0.15 | 0.875 | 0.875 | |
| LMT | 84.8 | 0.88 | 0.23 | 0.849 | 0.848 | |
| Average | 85.25 | 0.86 | 0.16 | 0.85 | 0.85 | |
| K-means imputation | SVM | 83.66 | 0.85 | 0.19 | 0.835 | 0.83 |
| RF | 87.36 | 0.87 | 0.1 | 0.87 | 0.87 | |
| MLP | 85.18 | 0.88 | 0.22 | 0.85 | 0.85 | |
| LMT | 86.92 | 0.89 | 0.19 | 0.868 | 0.868 | |
| Average | 85.78 | 0.87 | 0.18 | 0.86 | 0.85 | |
| MLP imputation | SVM | 85.62 | 0.86 | 0.15 | 0.856 | 0.856 |
| RF | 86.27 | 0.85 | 0.09 | 0.866 | 0.869 | |
| MLP | 87.58 | 0.9 | 0.18 | 0.875 | 0.875 | |
| LMT | 85.38 | 0.88 | 0.19 | 0.857 | 0.856 | |
| Average | 86.21 | 0.87 | 0.15 | 0.86 | 0.86 | |
| SOM imputation | SVM | 84.31 | 0.85 | 0.17 | 0.842 | 0.843 |
| RF | 87.14 | 0.87 | 0.11 | 0.861 | 0.87 | |
| MLP | 88.23 | 0.89 | 0.1 | 0.879 | 0.881 | |
| LMT | 84.09 | 0.87 | 0.22 | 0.84 | 0.84 | |
| Average | 85.94 | 0.87 | 0.15 | 0.86 | 0.86 | |
| Deleting MV cases | SVM | 74.76 | 0.51 | 0.19 | 0.74 | 0.73 |
| RF | 75.81 | 0.5 | 0.21 | 0.72 | 0.72 | |
| MLP | 72.92 | 0.44 | 0.17 | 0.73 | 0.73 | |
| LMT | 76.17 | 0.51 | 0.19 | 0.74 | 0.73 | |
| Average | 74.92 | 0.49 | 0.19 | 0.73 | 0.73 |
Table 3. Classification results from different type of missing value replacement methods.
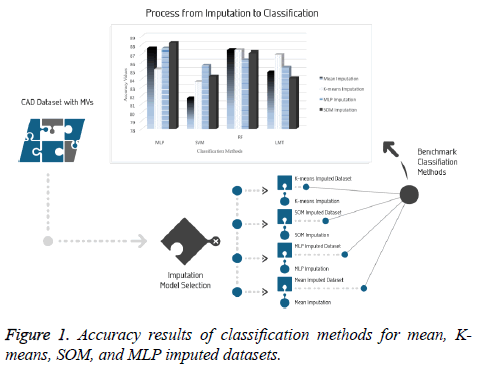
It is significant to evaluate the prediction performance of classifiers for CAD from different perspectives in clinical data analysis. Performance results based on evaluation metrics are presented in Figure 1.
For the original part of dataset with 277 samples, LMT achieved an accuracy ratio of 76.17% and the sensitivity value of 0.51, which was the top value for this dataset. This accuracy value remains under 7.49 points obtained by K-means imputation method and tested by the SVM classifier which is the lowest performance between imputations-classifications pairs.
The results indicated 87.58% accuracy on two datasets that are imputed using both the mean method and the MLP imputation method and tested by the MLP classifier. In addition, this dataset has the highest sensitivity, with a value of 0.9, as seen in Table 3. It is observed that the lowest accuracy (81.69%) and the lowest sensitivity (0.82) were obtained in the tests conducted using the SVM classifier.
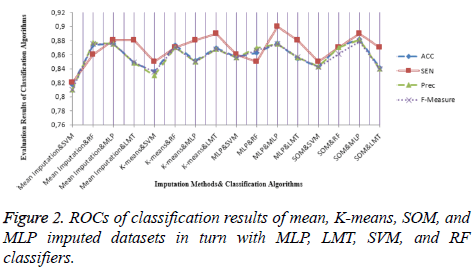
For the dataset prepared by the SOM imputation method, MLP achieved an accuracy ratio of 88.23%, which was the top value among the imputation-classification method pairs. This combination performed better than machine learning and mean method with regard to both MV imputation and classification. Moreover, other metrics were evaluated for all imputationclassification pairs and SOM imputation method has the best values obtained by MLP, with the accuracy of 88.23%, precision of 0.88, and F-measure of 0.879. Other metric results are presented in Figure 2.
Moreover, according to the average values of the classification results which are presented in Table 3, it is found that the dataset imputed by MLP is more stable than other imputed datasets and increases the performance of all classifiers in the study.
Discussion
Techniques developed for diagnosing CAD should provide considerable diversity in the style of clinical datasets. Sample size should be satisfactory and the connections between features should be determined. In this study, we propose a set of features relating to traditional risk factors such as gender, age, family history concurrently new para-clinical features such as RDW, MCV that were tested and proved to be efficient for identifying cases of CAD are included the model. The aim is to solve the MV problem of which these features store and finally to make a more stable diagnosis using imputed datasets. This study suggests alternative imputation procedures in the case of the lack of laboratory test as well other specific parameters. Thus, a cost- effective technique is constructed that does not need all potential laboratory tests for each suspect individual. It is a comforting situation for the patients on the financial terms.
When the MLP classifier is used on the dataset to which the MLP imputation algorithm is applied, it produces better results than the other methods, with a sensitivity of 0.9 and a specificity value of 0.18. According to the average classification results, the MLP imputation method produces more stable results than all the methods operated with different types of classifiers. The dataset produced by using the mean imputation method, which is widely used by researchers and has been used in this study as a reference, ranks fourth among the algorithm applications.
It has been inferred that MLP in particular is the most effective approach in the MV imputation process for the CAD dataset that includes continuous values when it is particularly tested with machine learning classifiers.
Acknowledgement
The authors thank for the support of all physicians in the Department of Cardiology of Mersin University, Mersin, Turkey
References
- Pope JH, Aufderheide TP, Ruthazer R, Woolard RH, Feldman JA, Beshansky JR, Griffith JL, Selker HP. Missed diagnoses of acute cardiac ischemia in the emergency department. N Engl J Med 2000; 342: 1163-1170.
- Tsumoto S. Problems with mining medical data. 24th Annual International Conference on Computer Software and Applications, IEEE Taiwan 2000; 467-468.
- Wang H, Wang S. Mining incomplete survey data through classification. Knowl Inf Syst 2010; 24: 221-233.
- Julian L, Salvador G, Francisco H. On the choice of the best imputation methods for missing values considering three groups of classification methods. Knowledge Inform Systems 2012; 32: 77-108.
- Gajawada S, Toshniwal D. Missing value imputation method based on clustering and nearest neighbours. Int J Future Comp Communication 2012; 1: 206-208.
- Zhang Z, Fang H, Wang H. Multiple imputation based clustering validation (miv) for big longitudinal trial data with missing values in ehealth. J Med Systems 2016; 40: 1-9.
- Richman MB, Trafalis TB, Adrianto I. Missing data imputation through machine learning algorithms. Artif Intell Med Environ Sci, Springer 2009; 153-169.
- Jerez JM, Molina I, Garcia-laencina PJ, Alba E, Ribelles N, Martín M, Franco L. Missing data imputation using statistical and machine learning methods in a real breast cancer problem. Artif Intell Methods 2010; 50: 105-115.
- Budayan C, Dikmen I, Birgonul MT. Comparing the performance of traditional cluster analysis, self-organizing maps and fuzzy C-means method for strategic grouping. Expert Syst Appl 2009; 36: 11772-11781.
- Jelinek HF, Yatsko A, Stranieri A,Venkatraman S. Novel data mining techniques for incomplete clinical data in diabetes management. Brit J Appl Sci Technol 2014; 4: 4591.
- Garcia-Laencina PJ, Sancho-Gomez JL, Figueiras-Vidal AR, Verleysen M. K nearest neighbours with mutual information for simultaneous classification and missing data imputation. Neurocomputing 2009; 72: 1483-1493.
- Chaudhuri BB, Bhattacharya U. Efficient training and improved performance of multilayer perceptron in pattern classification. Neurocomputing 2000; 34: 11-27.
- Jerez JM, Molina I, Laencina PJG, Franco L. Missing data imputation using statistical and machine learning methods in a real breast cancer problem. Artif Intell Med 2010; 50: 105-115.
- Fessant F, Midenet S. Self-organising map for data imputation and correction in surveys. Neural Comput Appl 2002; 10: 300-310.
- Gürbüz E, Kiliç E. A new adaptive support vector machine for diagnosis of diseases. Expert Syst 2014; 31: 389-397.
- Colak MC, Colak C, Kocaturk H, Sagiroglu S, Barutcu I. Predicting coronary artery disease using different artificial neural network models. Anatolian J Cardiol 2008; 8: 249-254.
- Yeh DY, Cheng CH, Chen YW. A predictive model for cerebrovascular disease using data mining. Expert Syst Appl 2011; 38: 8970-8977.
- Breiman L. Random forests. Mach Learn 2001; 45: 5-32.
- Royston P, Altman DG. Risk stratification for in-hospital mortality in acutely decompensated heart failure. JAMA 2005; 293: 2467-2468.