Biomedical Research

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.
Reach Us +44-7360-538437

Research Article - Biomedical Research (2018) Volume 29, Issue 15

Performance of loops in medical image compression

Pandian R*, Lalitha Kumari S, V Amala Rani, S Bestly Joe and Anne Frank Joe

Sathyabama University, Chennai, Tamil Nadu, India

*Corresponding Author:
Pandian R
Sathyabama University
Chennai, Tamil Nadu, India

Accepted date: June 27, 2018

DOI: 10.4066/biomedicalresearch.29-18-814

Visit for more related articles at Biomedical Research

Abstract

The storage facility of image and image transfer is an extensive appliance in image compression. Image compression techniques require the proper and effective transforms and encoding methods to reach the aim. In this work, discrete wavelet transform based image compression algorithm is used for decomposing the image. The effectiveness of different Encoder loops are analyzed based on the values of peak signal to noise ratio (PSNR), compression ratio (CR), means square error (MSE) and bits per pixel (BPP). The optimum encoding loop for compression is also found based on the results.

Keywords

CT image, Transform, Encoder, Symlet, Spiht, Encoder.

Introduction

In image storage and transmission memory requirements are always a challenge. Image compression algorithms are applied to overcome this, by the reduction of storage space and thus lead to sharing of documents easier. Image compression techniques formulate use of various transforms and algorithms. The algorithms can be normally classified as lossless and lossy compression [1,2].

Lossless compression technique is chosen, if there is no compromise on high quality output without any loss in consistency, whereas lossy compression technique is employed the areas, where a compromise is permissible in quality [3]. In lossy compression, there is negligible loss of quality, but the loss is too small to be visible. This technique is used in applications where a less amount of compromise on quality of image is tolerable. Initially, the image is usually decomposed with the help of proper transforms such as adaptive lifting, wavelet transform and wavelet packets [4]. Claypoole et al. worked an adaptive lifting scheme for image reduction and produced a MSE of 38.5 dB for Doppler, blocks etc. Claypoole et al. achieved a wavelet lifting scheme for image reduction with a PSNR of 42 dB [5]. Minh et al. used a wavelet transforms based image reduction for various images such as bike, cafe, water and X-rays [6]. Entropy was used as a figure of merit and it was establish as 5.90, in their work. Gemma et al. implemented a contourlet transform based compression for both peppers and Barbara images [7]. Entropy was adopted as a figure of merit and it was calculated as 30.47 dB in their work. Deng et al. used wavelet lifting scheme for various images such as rectangular, crosses, houses and peppers [8]. The performance is evaluated with their entropy values. Hoag used DWT-seam carving methodology for a test image and bitrate was used a figure of merit and it was found as 0.09 [9]. In their work, discrete wavelet transform is implemented for transforming the image and is primarily used for decomposition of images, whereas encoding is used to achieve the entire compression process and different type of Encoding methods are analyzed by various loop level to accomplish the image compression. The paper is structured in the following way. The transform methods and encoding algorithms are given below. Results, discussion and conclusion are below.

Wavelet Transform

In wavelet analysis a set of basic functions are used to represent the images. A single prototype function called the mother wavelets used for deriving the basis function, by translating and dilating the mother wavelet [10]. The wavelet transform can be viewed as a decomposition of an image in the time scale plane. In this work, Daubechies, symlets and coifles are used. The basic and compact wavelet, which is proposed by Daubechies, is orthonormal wavelets, which is called as Daubechies wavelet. It is designed with extremely phase and highest number of vanishing moments for a given support width. Associated scaling filters are minimum-phase filter. Daubechies wavelets are generally used for solving fractal problems, signal discontinuities, etc. The symlets are nearly symmetrical wavelet, which are also proposed in this work [11].

Encoding

In compression, for the reduction of the redundant data and elimination of the irrelevant data is performed by encoding methods. In this work, embedded zero tree wavelet (EZW), set partitioning in hierarchical Trees (SPIHT), spatial orientation tree wavelet (STW), wavelet difference reduction (WDR) and adaptively scanned wavelet difference reduction (ASWDR) are used [12].

Embedded Zero Wavelet

The embedded zero tree wavelet algorithm (EZW) is an image compression algorithm, in which embedded code represents a chain of binary decisions which distinguishes an image from the “null” image EZW which leads the compression results [13].

Set Partitioning in Hierarchical Trees

This algorithm uses a spatial orientation tree structure, which can be able to extract significant coefficients in wavelet domain, SPIHT does not have flexible features of bit stream but, it supports multi-rate, and it has high signal-to-noise ratio (SNR) and good image restoration quality, hence, it is appropriate for a high real-time requirement [14].

Spatial-Orientation Tree Wavelet

STW is basically the SPIHT algorithm; the only difference is that SPIHT is a little more cautious in its organization of coding output. The only difference between STW and EZW is that STW uses a different method to encoding the zero tree information. STW applies a state transition model. The locations of transformed values undergo state transitions, from one threshold to the next [15].

Wavelet Difference Reduction

The word difference reduction is used to represent the way in which WDR encodes the locations of significant wavelet transform values. Although WDR will not produce a higher PSNR the significance pass is the difference between WDR and the bit-plane encoding [16].

Result and Discussion

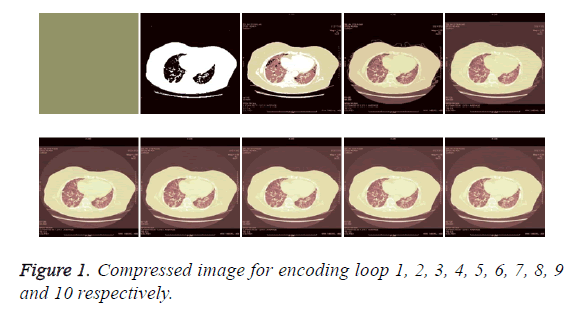
In this work, the evaluation of the proposed algorithms is performed on a CT image. Symlet wavelet based decomposition is employed for transforming the image [10]. The transformed image is then encoded by the above mentioned different methodologies. The ability of the compression algorithms are evaluated in terms of MSE, PSNR, compression ratio and Bits per pixel, which are tabulated in Table 1 and compressed image shown in Figure 1.

biomedres-encoding-loop

Figure 1: Compressed image for encoding loop 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 respectively.

Symlet/Loop 1 2 3 4 5 6 7 8 9 10
CR 14.99 17.7 21.09 23.87 26.6 30.71 36.09 42.74 51.2 59.32
PSNR 5.18 10.41 16.8 22.9 27.68 32.91 37.18 39.51 40.43 41.56
BPP 3.59 4.25 5.06 5.73 6.39 7.37 8.66 10.26 12.28 14.14
MSE 19690 5915 1357 333.7 110.9 33.31 12.46 7.28 5.89 3.49

Table 1: Performance evaluation of various encoding loops.

The quality of the reconstructed image is measured in terms of mean square error (MSE) and peak signal to noise ratio (PSNR) ratio [17], whereas the compression can be analyzed using the compression ratio and bits per pixel. The MSE is often called reconstruction error variance σq 2. The MSE between the original image f and the reconstructed image g at decoder is defined in equation (1).

MSE=σ2q=1/N × summation of (f (j, k)-g (j, k))2……………. (1)

Where the sum over j, k denotes the sum over all pixels in the image and N is the number of pixels in each image. From that the peak signal-to-noise ratio is defined as the ratio between signal variance and reconstruction error variance. The PSNR between two images having 8 bits per pixel in terms of decibels (dBs) is given in equation (2) [18].

PSNR=10log10 (2552/MSE) ………. (2)

The compression ratio of the image is given by number of bits in original image/no. of bits in compressed image. The original image, compressed image with symlet wavelet decomposition with encoding methods SPIHT for various encoding loops are shown in Table 1: 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 respectively.

If the encoding loop level is increased, the PSNR value gets increased, irrespective of the wavelet type. Both symlet 2 performed well at decomposition level 1, which is found in terms of PSNR value. At loop level 1, the PSNR value is very low. At higher loop levels, especially at 6 and 8, the symlet wavelet is not performed equally well. The PSNR values are almost moderate, compared to levels 1 and 2. The bits per pixel values are also obtained and the variations in its values are also following the PSNR value, since, it is related to the PSNR. The mean square error is also decreased if the level of loop is increased. It is wise to obtain a minimum value of error, which is also provided by symlet 1 with the last loop level of decomposition.

Conclusion

The main aim of this work is to obtain the high compression ratio, which is achieved by symlet wavelet with SPIHT. It is evident from the results that the nature of the encoding loop is the cause for the change in the performance values. Results clearly reveal that the number of encoding loops also plays an important role in the compression algorithm. It is also evident that the rise in the number of encoding loop leads to loss in information.

Acknowledgement

The author wishes to thank Dr. B. Sheela Rani, Director- Research, Sathyabama Institute of Science and Technology and Dr. B. Venkatraman, Scientists of Indira Gandhi Center for Atomic Research, Kalpakkam, and Government of India for the technical support provided by them.

References

Get the App