Research Paper - Journal of Applied Mathematics and Statistical Applications (2018) Volume 1, Issue 2
On the asymptotic behavior of the deficiency of some statistical estimators based on samples with random sizes
- *Corresponding Author:
- V.E. Bening
Faculty of Computational Mathematics and Cybernetics Lomonosov Moscow State University Russia
Tel: +7 495 939-31-21
E-mail: bening@yandex.ru
Accepted date: 26, 2018, 2018;
Citation: Bening VE. On the asymptotic behavior of the deficiency of some statistical estimators based on samples with random sizes.. J Appl Math Statist Appl. 2018;2(1):32-41.
Abstract
Due to the stochastic character of the intensities of information flows in high performance information systems, the size of data available for the statistical analysis can be often regarded as random. The purpose of this paper is to present some means for the comparison of the quality of estimators constructed from samples with random sizes with that of estimators constructed from samples with non-random sizes. As this means it is proposed to use the deficiency. It can be an illustrative characteristic of a possible loss of the accuracy of statistical inference if a random-size-sample is erroneously regarded as a sample with non-random size. It is heuristically shown that if the asymptotic distribution of the sample size normalized by its expectation is not degenerate, then the deficiency of a statistic constructed from a sample with random size whose expectation equals n with respect to the same statistic constructed as if the sample size was non-random and equal to n, grows almost linearly as n grows. A non-trivial behavior of the deficiency is possible only if the random sample size is asymptotically degenerate. This is the case considered in the paper where the deficiencies of statistics constructed from samples whose sizes have the Poisson, binomial and special three-point distributions, respectively, are considered. Some basic results dealing with some properties of estimators based on the samples with random sizes are also presented.
Keywords
Estimator, Risk function, Deficiency, Asymptotic deficiency, Sample with random size, Asymptotic expansions, Poisson distribution, Binomial distribution, Three-point distribution.
Introduction
Motivation for the consideration of statistics constructed from samples with random sizes
In most cases related to the analysis of experimental data, the number of random factors which influence observed objects is random and changes from one observation to anorher. Due to the stochastic character of the intensities of information flows in high performance information systems, the size of data available for the statistical analysis can be often regarded as random. In classical problems of mathematical statistics, the size of the available sample, i. e., the number of available observations, is traditionally assumed to be deterministic. In the asymptotic settings it plays the role of infinitely increasing known parameter. At the same time, in practice very often the data to be analyzed is collected or registered during a certain period of time and the flow of informative events each of which brings a next observation forms a random point process. Therefore, the number of available observations is unknown till the end of the process of their registration and also must be treated as a (random) observation. For example, this is so in insurance statistics where during different accounting periods different numbers of insurance events (insurance claims or insurance contracts) occur and in high performance information systems where due to the stochastic character of the intensities of information flows, the size of data available for the statistical analysis can be often regarded as random. Say, the statistical algorithms applied in high-frequency financial applications must take into consideration that the number of events in a limit order book during a time unit essentially depends on the intensity of order flows. Moreover, contemporary statistical procedures of insurance and financial mathematics do take this circumstance into consideration as one of possible ways of dealing with heavy tails. However, in other fields such as medical statistics or quality control this approach has not become conventional yet although the number of patients with a certain disease varies from month to month due to seasonal factors or from year to year due to some epidemic reasons and the number of failed items varies from lot to lot. In these cases the number of available observations as well as the observations themselves are unknown beforehand and should be treated as random to avoid underestimation of risks or error probabilities.
In asymptotic settings, statistics constructed from samples with random sizes are special cases of random sequences with random indices. The randomness of indices usually leads to that the limit distributions for the corresponding random sequences are heavy-tailed even in the situations where the distributions of non-randomly indexed random sequences are asymptotically normal [1-3]. For example, if a statistic which is asymptotically normal in the traditional sense, is constructed on the basis of a sample with random size having negative binomial distribution, then instead of the expected normal law, the Student distribution with power-type decreasing heavy tails appears as an asymptotic law for this statistic [1,4].
At the same time, according to the conventional logics of the statistical analysis, the distributions of the statistics (estimators, tests, etc.) to be used for the statistical inference should be known before the actual sample is observed in order to calculate critical values or thresholds. As a rule, asymptotic approximations by limit distributions of statistics are used instead of the exact distributions because the former are considerably easier computable than the latter. As this is so, in limit theorems of probability theory and mathematical statistics the centering and normalization of random variables are used to obtain non-trivial asymptotic distributions. It should be especially noted that to obtain reasonable approximation to the distribution of the basic random variables, both centering and normalizing values should be non-random. Otherwise the approximate distribution becomes random itself and, say, the problem of evaluation of quantiles required for the calculation of critical values or confidence intervals becomes senseless.
Throughout the paper we use conventional notation: 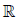 is the
set of real numbers,
is the
set of real numbers, 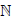 is the set of natural numbers, h(n) ~ f(n), n → ∞ if and only if
is the set of natural numbers, h(n) ~ f(n), n → ∞ if and only if 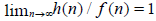 . The symbols
. The symbols 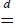 ,⇒ and
,⇒ and ![]() denote the coincidence of distributions, convergence in
distribution and the end of the proof, respectively.
denote the coincidence of distributions, convergence in
distribution and the end of the proof, respectively.
Consider a family of probability measures 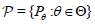 each
of which is defined on a measurable space (Ω,
each
of which is defined on a measurable space (Ω,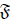 ) . Consider
a sequence of random variables (r.v.’s) X1, X2,… defined on a
measurable space (Ω,
) . Consider
a sequence of random variables (r.v.’s) X1, X2,… defined on a
measurable space (Ω,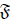 ) . Everywhere in what follows consider
the random variables X1, X2,… to be independent and identically
distributed (i.i.d) with common distribution Pθ . Let N1, N2,…
be a sequence of nonnegative integer random variables with
common distribution P defined on the same measurable space
so that for each n ≥ 1 the random variable Nn is independent of
the sequence X1, X2,… with respect to any measure Pθ from ρ . A random sequence N1, N2,… ( Ni with distribution P, i = 1, 2,…)
is said to be infinitely increasing (Nn → ∞) in probability P, if
P (Nn≤ M) → 0 as n → ∞ for any M ϵ (0, ∞). For n ≥ 1, let Tn
= Tn (X1,…, Xn) be a statistic, that is, a measurable function of
the r.v.’s X1,…, Xn. For each n ≥ 1 define the r.v. TNn by letting:
) . Everywhere in what follows consider
the random variables X1, X2,… to be independent and identically
distributed (i.i.d) with common distribution Pθ . Let N1, N2,…
be a sequence of nonnegative integer random variables with
common distribution P defined on the same measurable space
so that for each n ≥ 1 the random variable Nn is independent of
the sequence X1, X2,… with respect to any measure Pθ from ρ . A random sequence N1, N2,… ( Ni with distribution P, i = 1, 2,…)
is said to be infinitely increasing (Nn → ∞) in probability P, if
P (Nn≤ M) → 0 as n → ∞ for any M ϵ (0, ∞). For n ≥ 1, let Tn
= Tn (X1,…, Xn) be a statistic, that is, a measurable function of
the r.v.’s X1,…, Xn. For each n ≥ 1 define the r.v. TNn by letting:
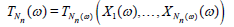
for every elementary outcome ω ϵ Ω. Assume that for each θ ϵ Θ there exists:
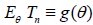
where ,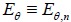 is the expectation w.r.t. distribution ,
is the expectation w.r.t. distribution , 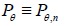 of Tn . We will say that the statistic Tn is asymptotically normal,
of Tn . We will say that the statistic Tn is asymptotically normal,
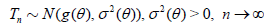 ,
,
if
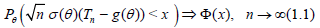
for each θ ϵ Θ.
The following statement describes the change of the limit law of an asymptotically normal statistic when the sample size is replaced by a r.v. (Theorem 3.3.2) [5].
Lemma 1.1. Assume that Nn → ∞ in probability P as n → ∞. Let the statistic Tn be asymptotically normal in the sense of
(1.1) . Then a distribution function F(x) such that
 ,
,
exists if and only if there exists a distribution function Q(x) satisfying the conditions Q(0) = 0 ,
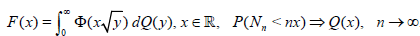 .
.
The concept of deficiency
Before turning to the general case of statistics constructed from samples with random size, that is the main aim of the present paper, let us recall the notion of a deficiency of a statistical estimator for the traditional case where the sample size is nonrandom [6].
Suppose that Tn (X1,…, Xn) and Tn (X1,…, Xn) are two
competing estimators of g(θ), θ ϵ Θ based on n observations X1,…, Xn and let their expected squared errors (risk functions)
be denoted by 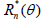 and
and 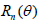 , respectively. An interesting
quantitative comparison can be obtained by taking a viewpoint
similar to that of the asymptotic relative efficiency (ARE) of
estimators, and asking for the number m(n) of observations
needed by estimato Tm(n) (X1,…, Xm(n)) to match the performance
of Tn* (X1,…, Xn) (based on n observations). The asymptotic (as n
→ ∞) comparison of the two estimators involves the comparison
of m(n) with n, and this can be carried out in various ways.
Although the difference m(n) - n seems to be a very natural
quantity to examine, historically the ratio n / m(n) was preferred
by almost all authors in view of its simpler behavior. The first
general investigation of m(n) - n was carried out by Hodges
and Lehmann [5]. They name m(n) - n the deficiency of Tn with
respect to Tn* and denote it as:
, respectively. An interesting
quantitative comparison can be obtained by taking a viewpoint
similar to that of the asymptotic relative efficiency (ARE) of
estimators, and asking for the number m(n) of observations
needed by estimato Tm(n) (X1,…, Xm(n)) to match the performance
of Tn* (X1,…, Xn) (based on n observations). The asymptotic (as n
→ ∞) comparison of the two estimators involves the comparison
of m(n) with n, and this can be carried out in various ways.
Although the difference m(n) - n seems to be a very natural
quantity to examine, historically the ratio n / m(n) was preferred
by almost all authors in view of its simpler behavior. The first
general investigation of m(n) - n was carried out by Hodges
and Lehmann [5]. They name m(n) - n the deficiency of Tn with
respect to Tn* and denote it as:
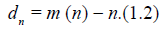
Suppose that for n → ∞, the ratio n / m(n) tends to a limit b, the asymptotic relative efficiency of Tn (X1,…, Xn) with respect to Tn* (X1,…, Xn) . If 0 < b< 1, we have dn ~ (b-1 - 1) n and further asymptotic information about dn is not particularly revealing. On the other hand, if b=1, the asymptotic behavior of dn, which may now be varying from o(1) to o(n), does provide important additional information.
If limn n →∞dn exists, it is called the asymptotic deficiency of Tn with respect to Tn* and denoted d. At points where no confusion is likely, we shall simply call d the deficiency of Tn with respect to Tn*.
The deficiency of Tn relative to Tn* will then indicate how many observations one loses by insisting on Tn , and thereby provides a basis for deciding whether or not the price is too high. If the risk functions of these two estimators are:
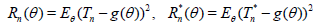 ,
,
then, by definition, dn(θ) = dn = m(n) - n, for each n, may be found from
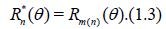
In order to solve (1.3), m(n) has to be treated as a continuous variable. This can be done in a satisfactory manner by defining Rm(n)( θ) for non-integer m(n) as:
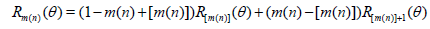 [6].
[6].
Generally Rn*(θ) and Rn(θ) are not known exactly and we have to use approximations. Here these are obtained by observing that Rn*(θ) and Rn(θ) will typically satisfy asymptotic expansions (a.e.) of the form:
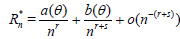 , (1.4)
, (1.4)
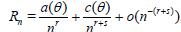 , (1.5)
, (1.5)
for certain a(θ), b(θ) and c(θ) not depending on n and certain constants r > 0, s > 0. The leading term in both expansions is the same in view of the fact that ARE is equal to one. From (1.2) - (1.5) is now easily follows that [6]
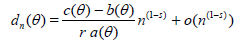 . (1.6)
. (1.6)
Hence,
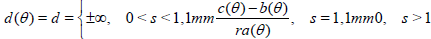 . (1.7)
. (1.7)
A useful property of deficiencies is the following (transitivity):
if a third estimator 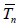 is given, for which the risk
is given, for which the risk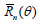 also
has an expansion of the form (1.5), the deficiency d of
also
has an expansion of the form (1.5), the deficiency d of 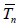 with
respect to Tn* satisfies the relation d = d1+ d2, where d1 is the
deficiency of Tn* with respect to Tn and d2 is the deficiency of Tn
with respect to Tn*.
with
respect to Tn* satisfies the relation d = d1+ d2, where d1 is the
deficiency of Tn* with respect to Tn and d2 is the deficiency of Tn
with respect to Tn*.
The situation where s = 1 seems to be the most interesting one. Hodges and Lehmann [6] demonstrate the use of deficiency in a number of simple examples for which this is the case (for testing problems see also [7-10]).
The purpose and structure of the paper
The purpose of this paper is to present some means for the comparison of the quality of estimators constructed from samples with random sizes with that of estimators constructed from samples with non-random sizes. As this means we propose to use the deficiency. It can be an illustrative characteristic of a possible loss of the accuracy of statistical inference if a randomsize- sample is erroneously regarded as a sample with nonrandom size. The present paper develops the research started [3] and presents a number of applications of the deficiency concept in problems of point estimation in the case when the number of observations is random.
Section 2 contains main results. First, in Section 2.1 we heuristically show that if the d.f. Q(x) in Lemma 1.1 is not degenerate, then the deficiency of a statistic constructed from a sample with random size whose expectation equals n with respect to the same statistic constructed as if the sample size was non-random and equal to n, grows almost linearly as n grows. A non-trivial behavior of the deficiency is possible only if the random sample size is asymptotically degenerate. This is the case considered in Sections 2.3, 2.4 and 2.5 where the deficiencies of statistics constructed from samples whose sizes have the Poisson, binomial and special three-point distributions, respectively, are considered. Section 2.2 contains some preliminary basic results dealing with some properties of estimators based on the samples with random sizes. Sections 3 - 5 contain results concerning deficiencies of asymptotic quantiles.
In this paper we focus on the case where the sample size is independent of the r.v.’s forming the sample. This assumption, first, is made for the sake of simplicity of the methods used to obtain the qualitative results. Second, in many applied problems this assumption does not contradict the essence of the problem. For example, this is so when the data is accumulated within a prescribed time interval (a month, a year, etc.), but the informative events form a stochastic flow. This situation is typical for financial and insurance practice or any other field of activities with accounting periods. Moreover, the independence of X1, X2,… is not crucial since basic Lemma 1.1 can be proved without this assumption [5]. Third, most papers considering non-independent sample sizes deal with the case of asymptotically degenerate indexes. This is just the case yielding non-trivial results in the present paper. It seems that using martingale techniques or imposing some concrete conditions on the character of dependence between the sample elements and the sample size, the results of this paper can be extended for the non-independent case.
Deficiencies of Some Estimators Based on the Samples with Random Size
The asymptotic behavior of the deficiency of a statistic constructed from a sample with random size
The interpretation of the deficiency as the number of additional observations required to attain the same quality here needs to be refined since this number becomes random in random-sizesamples problems. In order to circumvent this difficulty assume that the r.v.’s N1, N2,… are parameterized by their expectations:
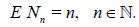
This assumption will enable us, instead of comparing random variables, to compare their easily tractable parameters.
Before we construct the exact formulas for the deficiencies so
tractable, we have to make some important heuristic comments
concerning the boundedness of the deficiency as a function of
the parameter n. By X without any indexes we will denote a
r.v. with the standard normal distribution N(0, 1). Let Tn be an
asymptotically normal (1.1) (with σ(θ) = 1) statistic constructed
from the sample X1, X2,…,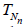 be (the same) statistic constructed
from the random-size-sample
be (the same) statistic constructed
from the random-size-sample 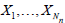 . Assume that
. Assume that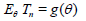 ,
, ![]() , implying
, implying ![]() ,
, ![]() (Theorem 2.1). Denote,
(Theorem 2.1). Denote,
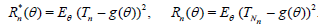
From Lemma 1.1, for n large enough we have the approximate relations:
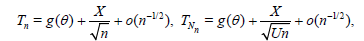
Where,
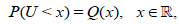
and the r.v.’s X and U are independent. Therefore,
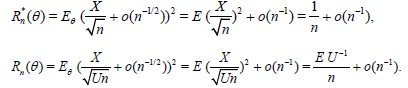
Equating Rn*(θ) and Rm(n)( θ) we obtain,
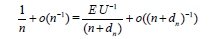
or
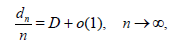
Where,
D = E U−1 −1.
So, in general, if EU−1 ≥ 1, then dn = O(n) . And the only possibility for dn to be o(n) and, in particular, to remain bounded, is the case:
E U−1 =1.
In general, if in addition to the conditions of Lemma 1.1, the family {Nn / n}n ≥ 1 is uniformly integrable, then the conditions of Lemma 1.1 and E Nn = n imply that EU =1, so that by the Jensen inequality we have EU−1 ≥ 1 with the equality attainable if and only if
P (U =1) =1.
In other words, for the deficiency dn to be bounded in n, it is necessary that the sample size Nn should be asymptotically degenerate in the sense that
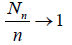
in probability as n → ∞. This property is inherent in sample sizes with the Poisson, binomial and special three-point distributions considered in the present paper.
It is worth noting that an example of geometrically distributed Nn for which the limit r.v. U as the exponential distribution vividly illustrates the possibility of the deficiency to be unbounded since in this case the Fréchet distribution of the r.v. U-1 has the infinite first moment.
Summarizing the abovesaid we conclude that if the d.f. Q(x) in Lemma 1.1 is not degenerate, then the deficiency of a statistic constructed from a sample with random size whose expectation equals n with respect to the same statistic constructed as if the sample size was non-random and equal to n, grows almost linearly as n grows. A non-trivial behavior of the deficiency is possible only if the random sample size is asymptotically degenerate. This is the case to be considered in the present paper.
Some properties of estimators based on the samples with random sizes
Assume that for each n ≥ 1 the r.v. Nn takes only natural values
(i.e., ![]() ) and is independent of the sequence X1, X2,…
Everywhere in what follows the r.v.’s X1, X2,… are assumed
independent and identically distributed with distribution
depending on
) and is independent of the sequence X1, X2,…
Everywhere in what follows the r.v.’s X1, X2,… are assumed
independent and identically distributed with distribution
depending on 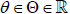 .
.
Recall that we assume that,
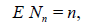
that is, the expected sample size equals the sample size for the case where it is non-random, that is, the r.v. Nn is parameterized by its expectation n.
Theorem 2.1.
1. If
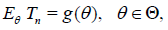
Then,
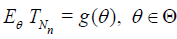 .
.
2 . Let
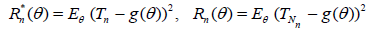 .
.
Assume that there exist numbers a(θ), b(θ), C(θ) > 0, α > 0, r > 0 and s > 0 such that
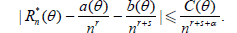
Then,
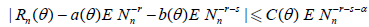 .
.
Proof: The desired relations can be easily obtained by the formula of total probability formula. Namely, we obviously have
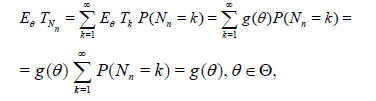
and
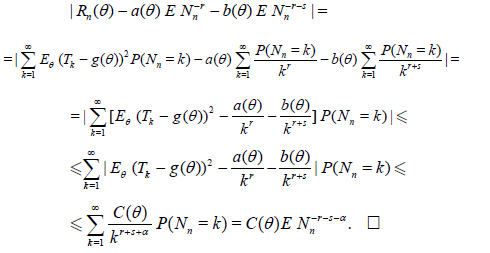
Corollary 2.1. Let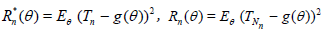
. Assume that there exist numbers a(θ), b(θ), r > 0 and s > 0 such that
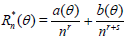 .
.
Then,
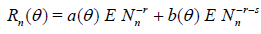 .
.
Consider some examples.
1. Let observations X1,…, Xn have expectation EθX1 = g(θ) and variance DθX1= σ2(θ). The customary estimator for g(θ) based on n observation is
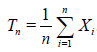 .(2.1)
.(2.1)
This estimator is unbiased and consistent, and its variance is
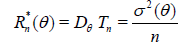 . (2.2)
. (2.2)
If this estimator is based on the sample with random size, then we have (see Corollary 2.1)
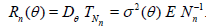 (2.3)
(2.3)
2. Now, if g(θ) is given, for σ2(θ) we consider the estimator of the form
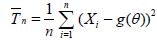 . (2.4)
. (2.4)
This estimator is unbiased and consistent, and its variance is
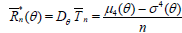 , (2.5)
, (2.5)
Where, 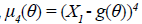 . For this estimator based on a sample
with random size we have
. For this estimator based on a sample
with random size we have
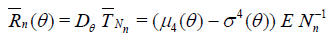 . (2.6)
. (2.6)
3. In the preceding example suppose that g(θ) is unknown and instead of (2.4) we consider any estimator of the form
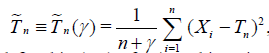 ,
, 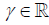 (2.7)
(2.7)
with Tn defined in (2.1). If γ ≠ -1, this estimator is not unbiased but may have a less expected squared error than the unbiased estimator with γ = -1. One easily obtains (3.6) [6].
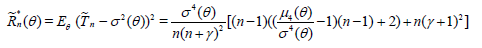
and hence,
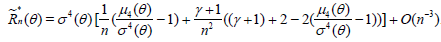 . (2.8)
. (2.8)
Using Theorem 2.1 we have
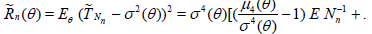
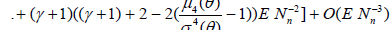 . (2.9)
. (2.9)
Deficiencies of some estimators based on samples with random size having the Poisson distribution
When the deficiencies of statistical estimators constructed from
samples of random size 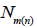 and the corresponding estimators
constructed from samples of non-random size n (under the
condition ENn = n) are evaluated, we actually compare the
expected size m(n) of a random sample with n by means of the
quantity dn = m(n) - n and its limit value.
and the corresponding estimators
constructed from samples of non-random size n (under the
condition ENn = n) are evaluated, we actually compare the
expected size m(n) of a random sample with n by means of the
quantity dn = m(n) - n and its limit value.
We will now apply the results of Section 2.2 to the three examples. We begin with the case of the Poisson-distributed sample size. Let Mn be the Poisson r.v. with parameter n – 1, n ≥ 2, i.e.
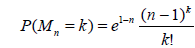 , k=0,1,....
, k=0,1,....
Define the random sample size as Nn = Mn + 1. Then, obviously, ENn = n and
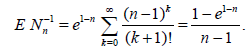
Expanding the exponent in the Taylor series, we easily obtain that
 . (2.10)
. (2.10)
The deficiency of 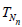 relative to Tn (see (2.1)) is given by (2.2),
(2.3), (2.10) and (1.7) with r = s = 1, a(θ) = σ2(θ), b(θ) = 0, c(θ)
= σ4(θ), and hence, is equal to
relative to Tn (see (2.1)) is given by (2.2),
(2.3), (2.10) and (1.7) with r = s = 1, a(θ) = σ2(θ), b(θ) = 0, c(θ)
= σ4(θ), and hence, is equal to
d =1.
Similarly, the deficiency of 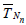 relative to
relative to 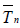 (see (2.4)) is
given by (2.5), (2.6), (2.10) and (1.7) with r = s = 1, a(θ) = c(θ)
= μ4(θ) - σ4(θ), b(θ) = 0, and hence, is equal to
(see (2.4)) is
given by (2.5), (2.6), (2.10) and (1.7) with r = s = 1, a(θ) = c(θ)
= μ4(θ) - σ4(θ), b(θ) = 0, and hence, is equal to
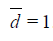 .
.
Now consider the third example (see (2.7)). We have
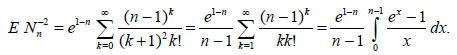
Using the Bernoulli – L’H ˆ o pital principle we obtain
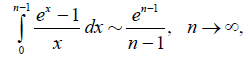
and
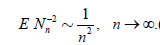 . (2.11)
. (2.11)
Now the deficiency of  with respect to
with respect to 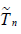 (see (2.7)) is given
by (2.8), (2.9), (2.11) and (1.7) with r = s = 1 and hence, is
equal to
(see (2.7)) is given
by (2.8), (2.9), (2.11) and (1.7) with r = s = 1 and hence, is
equal to
whereas the deficiency of  (γ1) with respect to
(γ1) with respect to (γ2) (see
(2.7)) is given by (2.10), (2.11) and (1.7) with r = s = 1 and
hence, is equal to
(γ2) (see
(2.7)) is given by (2.10), (2.11) and (1.7) with r = s = 1 and
hence, is equal to
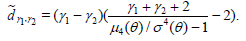
Thus, the classical  (0) is better than
(0) is better than  (-1) , if
(-1) , if
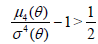 ,
,
with the situation reversed, if
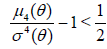 .
.
In particular, if X1 is normal, then
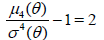
and
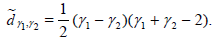
One can therefore save an expected 3 / 2 observations by using
the biased estimator  (0) . The best value of γ in the normal
case is γ = 1 for which
(0) . The best value of γ in the normal
case is γ = 1 for which 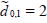 and which therefore provides an
additional saving 1 / 2 observations.
and which therefore provides an
additional saving 1 / 2 observations.
These examples illustrate the following statement.
Theorem 2.2. Assume that there exist numbers a(θ), b(θ) and k1, k2 such that
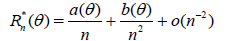
and
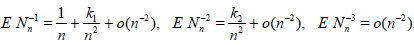
Then the asymptotic deficiency of 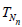 with respect to Tn is equal
to
with respect to Tn is equal
to
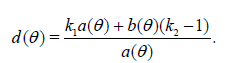
The proof follows from Theorem 2.1, (1.6) and (1.7).
Deficiencies of some estimators based on samples with random size having the binomial distribution
In this Section the results obtained above will be applied to the
calculation of the deficiencies of the estimators Tn , 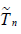 ,
, 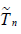 (see (2.1), (2.4) and (2.7)) constructed from samples whose sizes are
random and have the binomial distribution.
(see (2.1), (2.4) and (2.7)) constructed from samples whose sizes are
random and have the binomial distribution.
Using the definition of the binomial distribution we directly obtain the following statement.
Lemma 2.1. Let the r.v. Bn have the binomial distribution with the parameters m(n - 1), n ≥ 2 and p = 1 / m, where m ≥ 2 is a fixed natural number. Define the r.v. Nn as
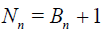 .
.
Then, as n → ∞,
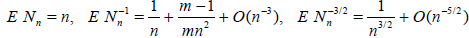 .
.
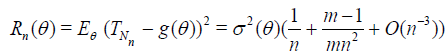
Lemma 2.1 and relations (2.3), (2.6) and (2.9) yield the following result.
Theorem 2.3. Let the r.v. Bn have the binomial distribution with the parameters m(n - 1), n ≥ 2 and p = 1 / m, where m ≥ 2 is a fixed natural number. Put Nn = Bn + 1. Then,
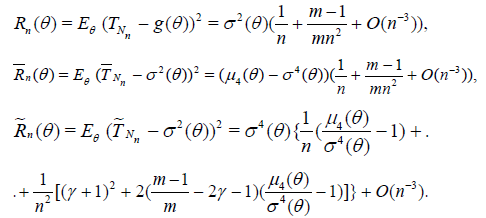
Corollary 2.2. Under the conditions of Theorem 2.3 the
asymptotic deficiencies of the estimators 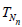 ,
,  and
and  with
respect to the corresponding estimators Tn,
with
respect to the corresponding estimators Tn, 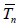 and
and 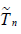 has the
form
has the
form
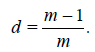
Deficiencies of some estimators based on samples with random size having a three-point symmetric distribution
In this Section we will consider the case where the random sample size Nn has the symmetric distribution of the form
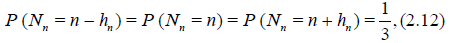
where the sequence of natural numbers hn < n satisfies the condition
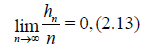
that is, hn = o(n) as n → ∞. It is easy to see that (2.12) and (2.13 imply that Nn / n → 1 in probability as n → ∞.
Lemma 2.2. Let the r.v. Nn have distribution (2.12) under condition (2.13) . Then ENn = n and, as n → ∞,
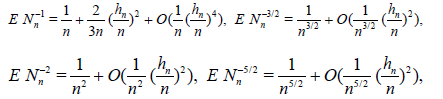
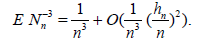
The proof follows from the easily verified equalities
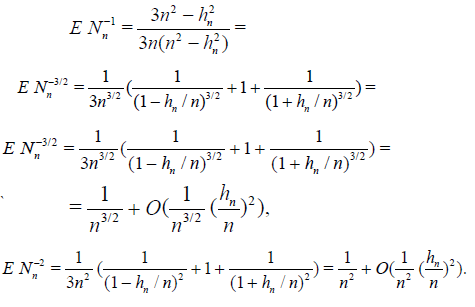
The asymptotic formulas for ![]() and
and 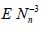 are established
in a similar way.
are established
in a similar way.
This Lemma and formulas (2.3), (2.6) and (2.9) directly imply the following statement.
Theorem 2.3. Let the r.v. Nn have distribution (2.12) under condition (2.13) . Then,
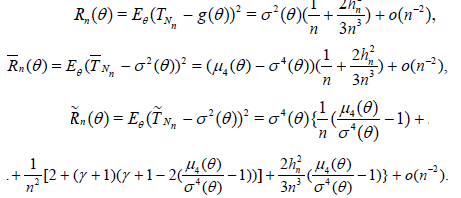
Corollary 2.3. Let the conditions of Theorem 2.3 hold and
Then the asymptotic deficiency of the estimators 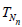 ,
, 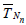
 and with respect to the corresponding estimators Tn,
and with respect to the corresponding estimators Tn, 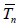 and
and 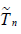 has the form
has the form
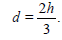
It is worth noting that in Corollary 2.3 h can be arbitrarily large. Therefore the finite asymptotic deficiency d considered in Corollary 2.3 can be arbitrarily large. This is in full correspondence with the conclusion of Section 2.1.
Asymptotic Deficiency and Quantiles
For n ≥ 1 let Tn = Tn(X1,…, Xn) be a statistic, that is, a measurable function of the r.v.’s X1,…, Xn. The asymptotic quantile of order α, α ϵ (0, 1) (the α – quantile) of statistic Tn is the value c*α (n) for which
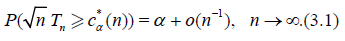
Using Taylor’s formula one has
Lemma 3.1. Suppose that the distribution function of 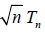 satisfies (uniformly in
satisfies (uniformly in 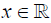 ) the relation
) the relation
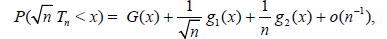
Where, G(x), g1(x), g2(x) are sufficiently smooth functions. Then,
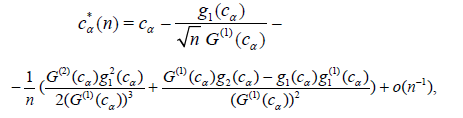
Where, G(cα) = 1 - α.
Corollary 3.1. Let δn → 0, n → ∞. Then under the conditions of
Lemma 3.1 uniformly in 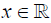
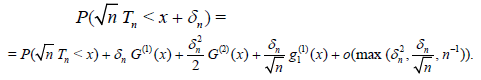
Now consider a statistic Sn = Sn(X1,…, Xn) other than Tn having α – quantile cα(n)
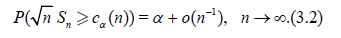
Suppose that:
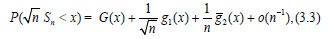
Where, ![]() are some smooth
functions. Define the sequence of positive integers
are some smooth
functions. Define the sequence of positive integers 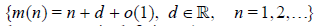 by the relation ( d is
the asymptotic deficiency)
by the relation ( d is
the asymptotic deficiency)
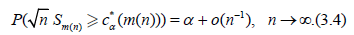
Theorem 3.1. Under the conditions of Lemma 3.1 and (3.3) the asymptotic deficiency d equals
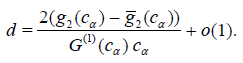
Proof. It follows from (3.1) and Lemma 3.1 that
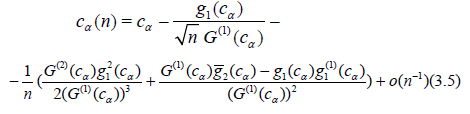
and
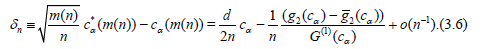
Moreover (3.4) implies
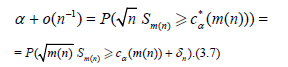
Using Corollary 3.1 we obtain
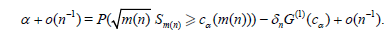
Then (3.2) and (3.6) imply
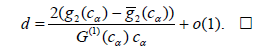
Now we apply these results to our exapmle.
Let X1, X2,… be i.i.d.r.v.’s with
![]()
Define
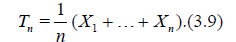
Suppose that the distribution of X1 satisfies the Cramer condition (C)
![]()
Under the conditions (3.8) and (3.10) (see Theorem 6.3.2) we have [8]
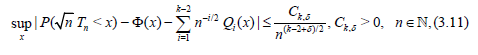
where the functions 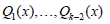 are defined in [8]
are defined in [8]
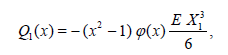
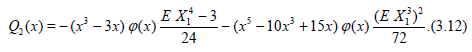
Carrying out the type of computation outlined above we arrive at the following simplified version of Lemma 1.1 (see (3.11)).
Lemma 3.2. Let the conditions (3.8) – (3.10) with k = 3 be satisfied and c*α (n) be defined by (3.9), then
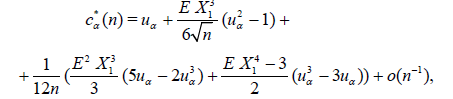
where uα = Ф-1(1 – α) denotes the upper α – point of the standard normal distribution.
Now let Y1, Y2,… be i.i.d.r.v.’s and
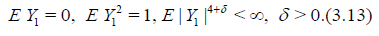
Define
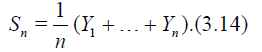
Suppose that
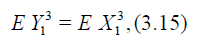
And
![]()
Applying Theorem 3.1 we obtain
Lemma 3.3. Under the above conditions of Lemma 3.2 and (3.13) - (3.16) the asymptotic deficiency d (see (3.4)) equals
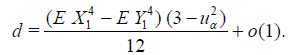
Samples with Random Sizes
Consider random variables N1, N2,… è X1, X2,…, defined on the
same probability space (Ω, A, P). The r.v.’s X1, X2,…, Xn will
be treated as observations with n being a non-random sample
size, whereas the r.v.’s Nn will be treated as random sample size
depending on the parameter  . For example, if the r.v. Nn
has the geometric distribution
. For example, if the r.v. Nn
has the geometric distribution
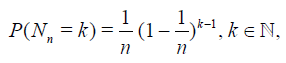
then
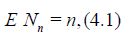
that is, the r.v. Nn is parametrized by its expectation n.
Assume that for each n ≥ 1 the r.v. Nn takes only natural values,
that is, 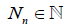 and are independent of the sequence X1, X2,…,
Everywhere in what follows consider the r.v.’s X1, X2,… to
be independent and identically distributed. By Hn = Hn(X1,..,
Xn) denote a statistic, that is, real measurable function of
observations X1,.., Xn. For each n ≥ 1 define tne statistic
and are independent of the sequence X1, X2,…,
Everywhere in what follows consider the r.v.’s X1, X2,… to
be independent and identically distributed. By Hn = Hn(X1,..,
Xn) denote a statistic, that is, real measurable function of
observations X1,.., Xn. For each n ≥ 1 define tne statistic 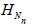 constructed from the sample of random size, that is
constructed from the sample of random size, that is
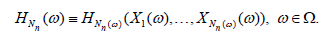
Now assume that the d.f. of the non-normalized statistic Hn admits an asymptotic expansion described by the following condition.
Condition A. There exist constants 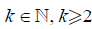 ,
, 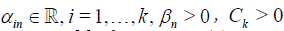 , a differentiable d.f. G(x) and
measurable functions gj(x), j = 1,…,k such that
, a differentiable d.f. G(x) and
measurable functions gj(x), j = 1,…,k such that
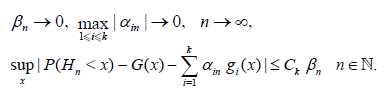
Lemma 4.1. If the condition A holds, then
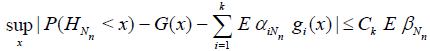 .
.
The proof is a simple exercise on the application of the formula of total probability.
Let X1, X2,… be i.i.d.r.v.’s and
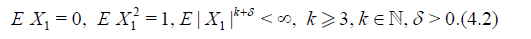
Define for each 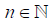
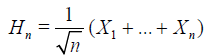 . (4.3)
. (4.3)
Suppose that the distribution of X1 satisfies the Cramer condition (C)
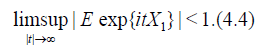
Taking into accopnt (4.2), (4.4) and Theorem 6.3.2 [8] we obtain
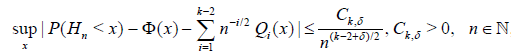 , (4.5)
, (4.5)
Where, [8]
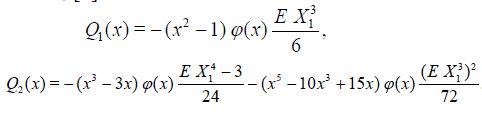 . (4.6)
. (4.6)
Using (4.5) and Lemma 4.1, one has
Lemma 4.2. Let the conditions (4.2) - (4.4) be satisfied, then
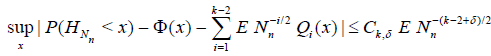 .
.
After these preliminaries (see (4.5) and Lemma 4.2), the following Lemma can be formulated.
Lemma 4.3. Suppose that the conditions (4.2) - (4.4) hold with k = 4, δ > 0 and there exist a, b such that
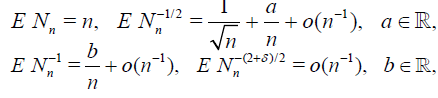
Then,
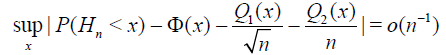
and
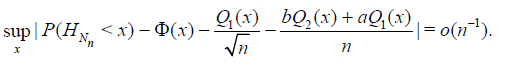
For n ≥ 1 let Hn = Hn (X1,.., Xn) be a statistic, that is, a measurable function of the r.v.’s X1,.., Xn. The asymptotic quantile of order α, α ϵ (0, 1) (the α – quantile) of statistic Hn is the value hα* (n) for which
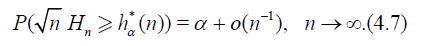
and we consider α – quantile of statistic 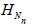 . That is the value
hα(n) for which
. That is the value
hα(n) for which
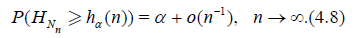
Taking into account (4.5), (4.6) and Lemma 3.1 we obtain
Lemma 4.4. Suppose that the conditions (4.2) - (4.4) hold with k = 4, δ > 0, then under the conditions of Lemma 4.3 α – quantiles hα* (n) and hα(n) admit the following asymptotic expansions
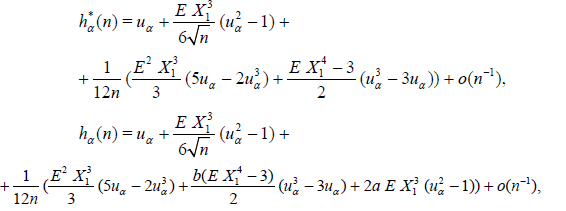
where Ф(uα) = 1 - α.
Define the sequence of positive integers 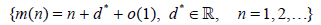 by the relation (d is the
asymptotic deficiency)
by the relation (d is the
asymptotic deficiency)
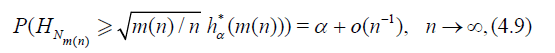
Now we have in analogy to Theorem 3.1
Theorem 4.5. Suppose that
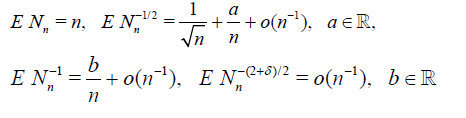
and
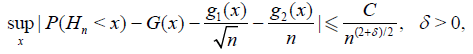
then the asymptotic deficiency d* (see. (4.9)) satisfies
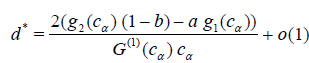
where G(cα) = 1 - α.
The result of these steps is the following Lemma.
Lemma 4.6. If the conditions of Lemma 4.3 are satisfied, we have (see. (3.12))
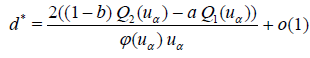
If
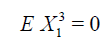 .
.
Then,
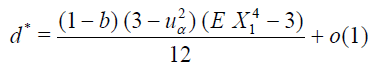
Discussion
The case of the samples with random size having a three-point symmetric distribution
In the previous section the results of section 3 were used to solve the main problem of this section. Here we briefly discuss another application of these results (see Lemma 4.2 and Theorem 4.5). Let Nn have a three-point distribution with parameter hn
-->