Research Article - Biomedical Research (2017) Volume 28, Issue 20
Medical image encryption based on multiple chaotic mapping and wavelet transform
Xiao Chen1,2* and Chun-Jie Hu1
1School of Electronic and Information Engineering, Nanjing University of Information Science and Technology, Nanjing 210044, PR China
2Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science and Technology , Nanjing 210044, PR China
- *Corresponding Author:
- Xiao Chen
School of Electronic and Information Engineering
Nanjing University of Information Science and Technology
PR China
Accepted date: November 01, 2017
Abstract
Images are now widely used in medical diagnosis. To protect the privacy of patients, the security of image information has been becoming more and more important. In order to increase the security of digital image encryption results, this paper proposes a new image encryption algorithm based on improved Logistic mapping, Arnold mapping, Kent mapping and wavelet transform. The Arnold mapping and the wavelet transform were used to shuffle image pixels and the Kent mapping was introduced to generate the control parameters in the Arnold mapping. The improved Logistic mapping for pseudo-random number generation and have done xor operation between the pixel value and the key value generated by the improved Logistic mapping. By analyzing and testing the secret key space, the information entropy, the correlation coefficient and the plaintext sensitivity, experimental results show that the algorithm has the advantages of simple structure, high security and is easier to apply.
Keywords
Arnold mapping, Wavelet transform, Logistic mapping, Image encryption
Introduction
With the rapid development of image processing technology, medical images are more and more important in diagnosing diseases. The new communication technologies results in sharing of information such as image information and position information [1] has become easier and faster. Countless private information is transmitted through the network, it is urgent to find a safe and security way to transmit image information [2], especially in medical domain to protect the privacy of patients. A number of encryption algorithms such as Data Encryption Standard (DES) have been developed, but it is not suitable for image encryption due to innate features of images such as abundant data size and high correlation among image pixels [3]. The chaotic system has characteristics like pseudo-random nature and initial condition sensitivity which are essential for cryptographic applications. It is computationally inexpensive and introduces a high level of randomness. This makes them highly suitable for image encryption.
The encryption methods based on chaos have been very popular [4–7]. Chaos-based encryption algorithm is first reported by Mattews [8]. Followed him, researchers have developed some algorithms for image encryption based on chaos [9-11]. The main concept of these encryption algorithms are scrambling and Diffusion. Scrambling permutes pixels in the image, without changing their pixel value. In the diffusion, the pixel values are changed orderly. An image encryption algorithm based on the general Arnold chaotic mapping was developed in literature [9]. In literature [10], it was shown that the method used the 3-dimensional reversible chaotic mapping. According to [11], it can be seen that defects still existed in them [9-10] - the secret key space of low-dimensional chaotic system is small, therefore it can’t resist the plaintext attack. ZHOU had designed an image encryption scheme using the hyper-chaotic function [12]. Compared with the low dimensional system, it has a larger key space, but a single chaotic system no longer meets the requirement of modern encryption.
To get a better encryption of medical images, a new image encryption scheme is proposed in this paper based on improved Logistic mapping, Arnold mapping, Kent mapping and wavelet transform. For scrambling, Arnold mapping and wavelet transform were used and improved Logistic mapping was used for diffusion. The results of experimental and comparison analysis both show that the proposed algorithm has the advantages of simple structure, high security and is easier to apply.
Method
Logistic mapping
Logistic mapping [13] is a very simple chaotic mapping. Its mathematical expression is
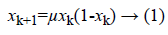
When μ ϵ [3.569946,4], Logistic mapping has a chaotic state. It generates a sequence{xn}, n=0,1,2.., which is non-periodic, non-convergence, and is very sensitive to initial values.
In order to improve the randomness of the sequence, the Logistic mapping and cubic mapping are combined to improve the performance of the sequences. It is defined by
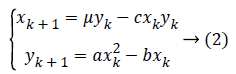
where a ϵ [0,4], bϵ [0,3], cϵ [0,4]. When the parameter μ=1.8, a=0.5, b=1, c=1, the system has two positive Laypunov exponents, indicating that the system is a hyper-chaotic system.
Kent mapping
Kent mapping is one of the nonlinear discrete chaotic mappings. It has been used to generate pseudo-random number in many applications such as spread spectrum communication and secure encryption. It is given by
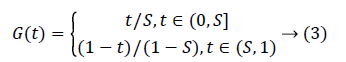
When t ϵ (0,1), S ϵ (0,1), the system is in the chaotic state.
Arnold mapping
Arnold mapping [14] is a special type of 2D invertible chaotic map that stretches and folds its orbits in phase space. It is described as
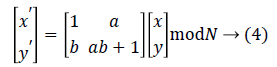
In the ith cycle, the coefficients a and b are obtained by the Eqs. (5) and (6) as follows
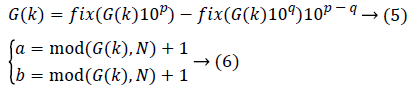
where s1 and s2 are two random number sequences generated by using Eq. (2) based on two Logistic mapping with the initial values x01 and x02, respectively.
The proposed method includes seven steps.
Step 1. Multilayer wavelet decomposition of the target image and the extraction of approximate component matrix.
Step 2. Input the initial value of the Kent mapping and parameter S and generate the control parameters of the Arnold mapping.
Step 3. The Arnold mapping scrambling equation is generated by the generated control parameters and the approximate component matrix is scrambled.
Step 4. According to the reverse order of the wavelet decomposition, reconstruct the scrambling matrix and get scrambled image I’.
Step 5. According to generated Arnold mapping scrambling equation in Step 3, scramble image I’ globally to get the scrambled image I”.
Step 6. Input the initial value of the improved Logistic mapping and iterative M*N to generate two-dimensional sequence. And then convert it according to the formula (7) to get a new two-dimensional sequence {x1(i)} and {y1(i)}, i=1,2, ….MN
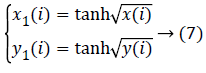
Step 7. Take a point in the image I” (set the point number is n). When the mod (n, 2) is even, the formula (8) is used to get a sequence K (n); otherwise the formula (9) is used to get a sequence K (n).
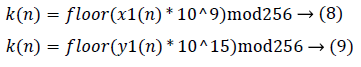
The decryption process is similar to the encryption process. As long as the correct key is obtained, the original image can be recovered according to the reverse operation of the encryption process.
Results
This paper used the classic 256 test image lena.bmp in simulation under Matlab7.0. When the parameters in the formula (2) is set to μ=1.8,a=0.5,b=1,c=1, the improved Logistic mapping is chaotic state. The adjacent pixel correlation distributions of the plain image and the ciphered image along the horizontal, vertical and diagonal directions are shown in Table 1.
| Direction | Plain image | Ciphered image | [16] | [17] | [18] |
|---|---|---|---|---|---|
| Horizontal | 0.9568 | 0.0098 | -0.0029 | 0.0204 | 0.0136 |
| Vertical | 0.9642 | -0.0089 | -0.0150 | 0.0017 | 0.0062 |
| Diagonal | 0.9351 | 0.0014 | 0.0129 | -0.0231 | 0.0175 |
Table 1: The correlation coefficient of adjacent pixels.
Discussion
Histogram analysis
Histogram is a kind of description of the spatial distribution of gray value of image. From the spatial distribution of gray value of Lena figure, the pixel distribution of the plaintext image is not uniform, and the pixel points of the encrypted image are evenly distributed. The gray level information of the plaintext image is well hidden in the encrypted image, which can resist the statistical attack.
Key space analysis
A good image encryption system should at least have a large key space to make the brute-force attacks impossible. In the proposed algorithm, the key space includes several parameters. In the scrambling stage, there are one control parameter, one initial value and the number of scrambling parameters N. The improved Logistic mapping has 4 control parameters and 2 initial values in the diffusion stage. If the precision of the number is 10-16 in the computer, the key space of the method is 10128. In the scrambling and diffusion processes, there is an extra outer loop, which implies that the key space is even larger. Therefore, the encryption system is large enough in the key space to resist all kinds of brute-force attacks.
Information entropy
Entropy is an important measure to evaluate the randomness of image, which is used to represent the degree of the disorder in a physical system. Its formula is
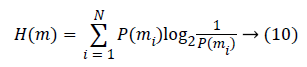
Where M is a random variable with N outcomes {m1,m2,…mn} and P(mi) is the probability mass function of outcome mi. For a ciphered image with 256 gray levels, the entropy should ideally be 8. The image encryption is to make the image in a disordered state. By using the formula (10), the information entropy of the plain image Lena is 7.5683, the information entropy of encrypted image is 7.9890. Compared with the algorithm in literature [15] (the information entropy of the algorithm is 7.978), the entropy is larger, which is very close to the theoretical value of 8. So it can be seen that the proposed encryption system can be regarded as a pseudo-random data generator and hence robust against frequency analysis.
Correlation coefficient
In digital images, the correlation between adjacent pixels is rather large. In order to examine and compare the correlation between the adjacent pixels of the plain text image and the encrypted image, the following procedure was carried out. First, 2000 pairs of two adjacent pixels (in horizontal, vertical, and diagonal directions) from an image were selected. Then, the correlation coefficient of each pair is calculated by using the following formulas [11]:
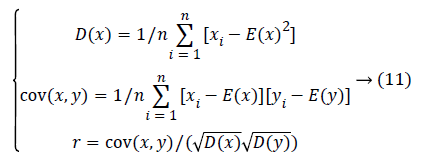
Where x and y are gray-scale values of two adjacent pixels in the image. E(x) is the expectation of x, D(x) is the variance of x and cov(x, y) is the covariance of x and y. R is adjacent pixel correlation coefficient.
The adjacent pixel correlation distributions of the plain image and the ciphered image along the horizontal, vertical and diagonal directions are analyzed. The point in the plaintext image is mostly concentrated around the diagonal, which means the vertical and horizontal coordinates of each point are almost equal, so the correlation of adjacent points is very strong. The points in the encrypted image are uniformly concentrated in the coordinates, there is no obvious relationship between the vertical and horizontal coordinates of each point, so the correlation of adjacent points is pretty much low. Furthermore, the correlation coefficients are shown in Table 1.
From Table 1, the plain text is highly related to the adjacent pixel image, the correlation coefficient is close to 1, instead of the cipher image correlation between adjacent pixels is smaller, The correlation coefficient is close to 0, indicating the adjacent pixels encrypted image is not related to the basic. Tab. 2 also lists the recently chaotic image encryption algorithm to get the correlation coefficients; the algorithm has a smaller correlation coefficient, which shows that the method has a very good diffusion performance.
Differential attack analysis
This purpose is intended to emphasize the diffusion property of an encryption system with respect to small changes in a plaintext image. This is important because the encryption system will be vulnerable to chosen-plain text attack. The diffusion performance of an image t of P1 encryption system is commonly measured by means of two criteria, number of pixel change rate (NPCR) and unified average changing intensity (UACI ) namely. The NPCR is used to measure the percentage of different pixel numbers between two images. Let P1(i, j) and P2(i, j) be the (i, j) pixel of two images P1 and P2, respectively, the NPCR is defined as,
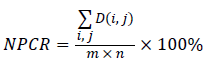
Where m and n are the width and D(i, j) is defined as
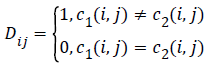
The second criterion, UACI is used to measure the average intensity of differences between the two images. It is defined as
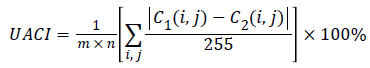
To a 256 gray scale image, the theoretical ideal NPCR is 99.6094% and the theoretical ideal UACI is 33.4635%. When a pixel in the encrypted image by using the proposed method is changed, NPCR is 99.6002% and UACI is 30.8319%. The results indicate that a slight change in the input image will result in a significant change in the output ciphered image. Therefore, the proposed method is robust against differential attack.
Conclusion
This paper presents a new image encryption algorithm based on the multiple chaotic mapping and wavelet transform. The Arnold mapping and the wavelet transform were used to shuffle image pixels and the Kent mapping was introduced to generate the control parameters in the Arnold mapping. The improved Logistic Mapping for pseudo-random number generation and have done xor operation between the pixel value and the key value generated by the improved Logistic mapping. The experimental analysis shows that the algorithm can achieve a good encryption effect, and that it can effectively resist statistical attack and plaintext attack. It has a large key space and the characteristics of strong robustness. In a word, it could have good practice and application in the field of image secure communication.
Acknowledgement
This work was supported in part by project grants from the six talent peaks project in Jiangsu Province (DZXX-006), in part by 333 high level personnel training project Jiangsu Province of China, in part by the Natural Science Foundation of Jiangsu Province of China (BK20161536), and in part by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
References
- Chen X, Zou S. Improved wi-fi indoor positioning based on particle swarm optimization. IEEE Sensors J 2017; 17: 7143-7148.
- Li C, Li S, Asim M, Nunez J, Alvarez G, Chen G. On the security defects of an image encryption scheme. Image Vision Comput 2009; 27: 1371-1381.
- Avasare M, Kelkar V. Image encryption using chaos theory, in 2015 Int Conference on Communication, Information & Computing Technology (ICCICT), 2015.
- Zhu C, Hu Y, Sun K. A new image encryption algorithm based on hyper-chaos system and cipher text staggered diffusion mechanism. J Elect Informat Technol 2012; 34: 1735-1743.
- Xu G, Guo X. A new image encryption based on chaotic system and the DNA computing. Comput Appl Res 2015; 32: 1766-1769.
- Guan Z, Huang F, Guan W. Chaos-Based Image Encryption Algorithm. Physics Letters A 2005; 346: 153-157.
- Kwok H, Tang W. A fast image encryption system based on chaotic maps with finite precision representation Chaos. Solitons Fractals 2007; 32: 1518-1529.
- Matthews R. On the derivation of a chaotic encryption algorithm. Cryptologia 1989; 13: 29-42.
- Zhang X, Fan J. A generalized cat chaotic map and its performance analysis. J Syst Simulat 2007; 19: 5578-5580.
- Li J, Feng Y, Yang X. An image encryption algorithm based on three-dimensional reversible chaotic map. Optic Tech 2008; 34: 918-923.
- Rhouma R, Safya B, Cryptanalysis of a new image encryption algorithm based on hyper-chaos. Physics Letters A 2008; 372: 5973-5978.
- Zhu C, Sun K. Cryptanalysis and improvement of a class of hyperchaos based image encryption algorithms. Acta Physica Sinica 2012; 61: 120503.
- Pareek N, Patidar V, Su K. Image encryption using chaotic logistic map. Image Vision Comput 2006; 24: 926-934.
- Kanso A, Ghebleh M. A novel image encryption algorithm based on a 3D chaotic map. Commun Nonlinear Sci Numer Simulat 2012; 17: 2943-2959.
- Deng S, Huang G, Chen Z. Adaptive image encryption algorithm based on chaotic maps. J Comput Appl 2011; 31: 1502-1511.
- Kanso A, Gheblen M. A novel image encryption algorithm based on a 3D chaotic map. Commun Nonlinear Sci Num Simulat 2012; 17: 2943-2959.
- Wang X, Lei Y. A novel chaotic image encryption algorithm based on water wave motion and water drop diffusion models. Optics Commun 2012; 285: 4033-4042.
- Xie G, Ding Y. Image encryption algorithms with variable confusion parameters based on Logistic mapping. Microelect Comput 2015; 32: 111-115.