Research Article - Biomedical Research (2019) Volume 30, Issue 1
Clustering of Zika virus epidemic using Gaussian mixture model in spark environment.
Lavanya K, Saira Banu J* and Prakhar Jain
School of Computer Science and Engineering, VIT University, Vellore, Tamil Nadu, India
- *Corresponding Author:
- Saira Banu J
School of Computer Science and Engineering
VIT University
Tamil Nadu, India
Accepted date: January 23, 2019
DOI: 10.35841/biomedicalresearch.30-18-1132
Visit for more related articles at Biomedical ResearchAbstract
Zika virus is a member of the virus family Flaviviridae as of 2016, no medications or vaccines have been developed for the prevention of the disease. It is spread by Aedes mosquitoes which are generally active during daytime. There was a widespread epidemic of Zika fever in 2015, which was caused by the Zika virus in Brazil. It also spread to other parts of North and South America and affected several islands in the Pacific, and Southeast Asia. The Zika virus dataset that we used is a huge dataset containing information about degree of spread of virus at various places in the North and South America, the number and type of cases recorded. In our study, we have performed Gaussian mixture model based clustering to group data points with similar attributes. These clusters can aid in the visualization of the spread of the virus during the epidemic. Entropy assisted ranking reduces the dataset by identifying least important attributes and optimizes the target dataset for higher accuracy and decision making. Gaussian mixture model (GMM) is implemented in spark environment using the machine learning library (MLlib). GMM is a probabilistic model that performs soft clustering by computing the probability of data points and placing them in various Gaussians (clusters). Spark performs parallel distributed processing to mine useful data by distributing datasets and creating resilient distributed dataset (RDD). Apache spark supports in-memory computations and scalability; therefore it works well for iterative algorithms like clustering in GMM.
Keywords
Gaussian mixture model, Spark, Zika virus
Introduction
Zika virus was initially recognized in monkeys in Uganda in 1947. Afterwards it was found in humans in 1952 in Uganda and the United Republic of Tanzania. Outbursts of Zika virus disease have been confirmed in Asia, Americas, Africa and the Pacific. The symptoms are generally minor and last for 2-7 days. Zika virus is generally transferred to people from the bite of an infected Aedes mosquito, mostly Aedes aegypti in humid areas. Aedes mosquitoes generally bite during the day, peaking during evening and dawn. Sexual transmission of Zika virus is also possible [1]. Zika fever can lead to the development of encephalitis.
Recent Zika pandemic caused an interest in its sudden emergence as a deadly human pathogen. The disease predicting data have a lot of uncertainties and therefore calculating its subgroup lets supervised learning to bring some accuracy concepts. The main goal of this research is to analyse the spread of Zika virus around the world by applying machine learning algorithm such as clustering based on Gaussian mixture model. These algorithms can also be applied to different diseases to analyse its spread and help in controlling the spread. It is difficult to mine useful information from huge Zika virus dataset. The ranking assisted entropy-based feature selection procedure discards noise-corrupted, insignificant and redundant features. It also reduces the dimensionality and thereby increasing accuracy.
The Gaussian mixture model is a method for performing soft clustering. The number of clusters (k) is predefined and the parameters are calculated using the expectation maximization (EM) Algorithm. The data-points may belong to multiple clusters based on individual probability and parameter values of the Gaussians. This model is useful for our research as it uses probability based clustering, and as there can be multiple type of Zika virus diagnosis, probability based clustering accurately clusters these data points such that a data point may belong to more than one cluster.
Big-data analytics is more vital in the current scenario of the world where intelligent decisions can make all the difference. Big companies, government organizations, and people at higher positions are gradually moving towards big data analytics to make important decisions and become more prevalent in the competitive world. Apache Spark was proposed in 2010 to incorporate the growing demand for big data analytics and distributed computing. Spark has a friendly Scala interface. Spark also implements incorporated provision for recurring data flows. We have used Spark as our big data engine as Spark implements MLlib which is a complete machine-learning library, over the Spark core along with other libraries. MLlib provides a very intelligible application program interface (API) for great value, machine-learning programs [2].
The structure of this paper is organized as follows. Sections II and III highlights the background study. Proposed system methodology is presented in sections IV and V and evaluation of the system is discussed in sections VI and VII.
Review of Literature
Revlin proposed a new method capable of approaching clinically important groups, based on patient Length of stay from a given dataset of patients. The Gaussian Mixture Model was able to capture the shorter, medium and longer stay patient terms and to define clinically important groups [3]. Kart-Leong developed a new procedure to train Gaussian mixture model for an image categorization problem. Learning of Gaussian mixture model factor with Markov random field is enhanced by considering a local neighborhood of maximal clique for learning each Gaussian mixture model sample [4]. Arindam proposed two methods to categorize physical activities performed by a various group of members from a tri-axial accelerometer. While comparing it was found that generally mean accuracy of hidden Markov model is indeed superior to Gaussian mixture model, but an improved total classification is accomplished with Gaussian mixture model. Both hidden Markov model and Gaussian mixture model are matched and found to be efficient but beat each other in diverse conditions [5]. Perez claims that good selection of parameters aids in making a precise segmentation of the corals and sorting the coral reef surfaces. When the clusters or k value is low, the textures could not be characterized in an apt manner and the images were likely to cause under segmentation, but when the clusters value is very high then the structure is over-fitted and the smallest areas were recognized too which did not add with the segmentation of the largest textures, affecting over segmentation [6]. Bei proposed a clustering algorithm based on probability density estimation, the spatial Gaussian mixture model (SGMM), for optical remote sensing Images to incorporate the spatial data, and an approximation algorithm based on expectation maximization is developed for the SGMM. The relationships between the Gaussian mixture model and probabilistic latent semantic analysis (PLSA) are analysed hypothetically in this paper, which shows that the SGMM can be observed as an addition to the Gaussian mixture model [7]. Heng-Chao proposed a novel framework for the probabilistic fault diagnosis under new data categories. GMM was applied as the pattern recognition algorithm, while its training was improved from conventional unsupervised learning to novel semi-supervised learning [8]. David in his paper develops a machine-learning library model capable for addressing the continuous growing need for scalable machine-learning applications. Situ MApReduce liTe (SMART)-MLlib provides a friendly Scala API for distributed machine-learning programs that perform over the Smart [2].
Background Study
Entropy
Entropy calculates the quantity of meaningful data in an attribute. Considering a dataset of ‘n’ samples it is formulated as:
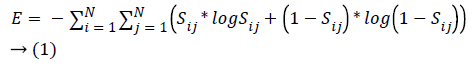
where Sij is the degree of similarity between two occurrences xi, yi based on information gain from the attributes, which determines the correlation between attributes and picks the attributes with higher resemblance.
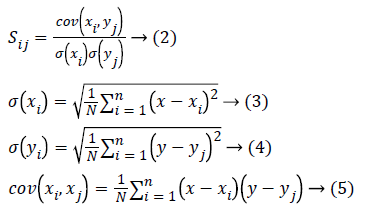
Gaussian mixture model
There are two types of clustering: hard clustering and soft clustering. In hard clustering the clusters do the overlap which means that a point either belongs to a cluster or it does not. In soft clustering, clusters may overlap which means that a point may belong to more than one cluster. Mixture models are a probabilistically-grounded way of performing soft clustering. A Gaussian mixture model is a probabilistic model that takes all the data points that are generated from a mixture of a finite number of Gaussian distributions with unknown parameters. Each cluster is a generative model which belongs to a probability distribution. There are two parameters: Mean and variance. Mixture models are the general form of k-means clustering which includes information about the covariance structure of the data along with the centers of the latent Gaussians. In GMM the probability of each point for different clusters are calculated and the clusters are adjusted to incorporate the changes in probabilities [9].
For example, if points are in 1D, initially let’s consider there are two Gaussians a, b with parameters as μa and μb, and x1, x2, x3,..., xn are the points in 1-dimension, then,
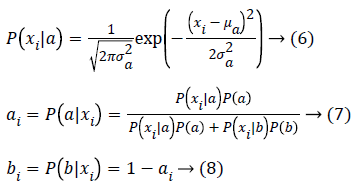
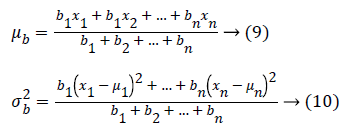
Comparing GMM with k-Means
Both GMM and K Means are commonly used clustering algorithms. Both require the number of clusters (k) as input, which may not be easy to determine. K means is a method for hard clustering, which means that a data point may only belong to one cluster. Also the clusters are formed using only mean value, which results in the circular shaped cluster. However, GMM uses mean and variance parameters, which results into elliptical shape cluster. GMM uses probability, so a data point may belong to multiple clusters. Therefore GMM based clustering is more flexible.
Spark
Apache Spark is a computing platform designed to be fast and general-purpose and easy to use. It saves time and money due to in-memory computations. It provides Parallel distributed processing, fault-tolerance on commodity hardware, scalability etc. It contains APIs for Scala, Python, Java and libraries for SQL, Machine Learning, Streaming, and Graph Processing. Spark can run on Hadoop clusters or as a standalone [10].
It uses resilient distributed dataset (RDD) which is a read-only collection of objects that can be operated on in parallel, separated across a set of machines that can be restored if a partition is lost. There are two types of RDD operations: Transformations and Actions.
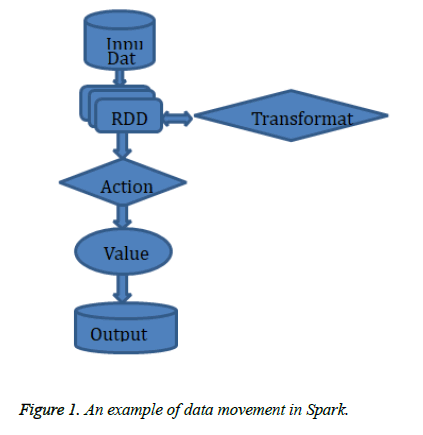
As shown in Figure 1, transformations take a resilient distributed dataset of one kind, and convert it into an RDD of a different type, using functions which are defined by the user. Actions, on the contrary, require an actual computation to be executed. Actions process a particular resilient distributed dataset and yield some result. Transformations and actions are both performed in parallel by Spark. The figure below demonstrates an example dataflow in Spark. Initially, data is included from the file system into an RDD. After loading, a series of transformations are executed on the RDD, and at last, an action is executed and the program is completed.
System Architecture
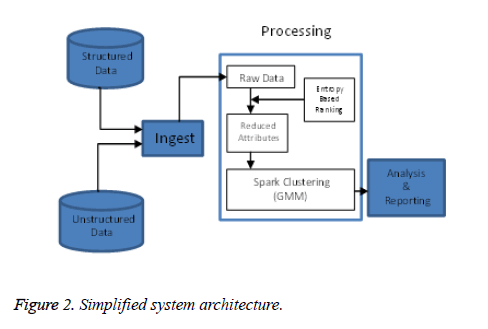
Figure 2, describes the architecture of the system. The system can take both structured and unstructured data. In the first step, the data is combined to create raw data. The data may contain a large number of records as it can be processed by Spark. The entropy-based ranking with Information Gain feature is applied on the raw data. It gives the ranking of all the attributes according to the Info. Gain coefficient value. The lowest ranked attributes can be removed from the dataset to reduce the complexity of the dataset. It also removes non-significant, missing, attribute values. Therefore by retaining the most significant information, the accuracy of the clustering algorithm is increased. The data is converted into numeric form for the scala Gaussian mixture model code. The Gaussian mixture model is implemented on the reduced Zika virus numeric dataset, which gives the parameters of the Gaussians as the output. These parameters are analysed to give the cluster information about the mean and variance from the dataset.
Methodology
Dataset
The Zika virus dataset was obtained from the Kaggle. The dataset is compiled by “Centres for Disease Control and Prevention” (CDC). It contained lakhs of records. To reduce the complexity the authors have considered the country as ‘United States’. In this dataset, after application of ranking, the number of non-zero records reduced to “1393” with “70” distinct locations within the United States like Alabama, Arizona, Florida etc. The locations could be classified as a state, county or a territory. In the dataset, there are 50 distinct ‘reported_date’ with 23 types of ‘data_fields’. These data fields represent the type of Zika found at that location. The Table 1 below represents all the attributes with corresponding notations.
| Attributes | Notations |
|---|---|
| Report_Date | RD |
| Location | LC |
| Location_Type | LT |
| Data_Feild | DF |
| Data_Feild_Code | DC |
| Time_Period | TP |
| Time_Period _Type | TT |
| Value | VL |
| Unit | UN |
Table 1: List of attributes with notations in the dataset.
The GMM scala code for performing clustering in Spark takes only numeric values for calculating the mean and co-variance of the Gaussians. The dataset contains String values which need to be converted to numeric values. Table 2 represents the possible ranges for the attributes and the code that authors have used to convert string data to numeric type data.
| Attributes | Possible range | Number of distinct values | Code |
|---|---|---|---|
| Report_date | (Jan, Feb, Mar, Apr, May, Jun) | 50 | 1.01 to 1.50 |
| Location | (Distinct locations within United States) | 70 | 2.01 to 2.70 |
| Location_type | (County, State, Territory) | 3 | 3.1 to 3.3 |
| Data_field | (Zika reported, Zika Confirmed, Zika not found,….,no specimen, lab positive) | 23 | 4.01 to 4.23 |
Table 2: Code for conversion to numeric form.
Ranking assisted entropy feature selection
Entropy defines a minimal Zika virus dataset from the original problem dataset by retaining high precision. The ranking sort discrete data according to the Information gain value of the attributes. The institution of ranking in entropy includes ordering, to estimate the performance of input data compared to each other. Table 3 gives the attribute ranking which uses Information gain ranking feature.

| Ranking | Info. gain | Attributes |
|---|---|---|
| 1 | 1.4496 | Report_date |
| 2 | Nominal | Location |
| 3 | 1.4836 | Location_type |
| 4 | 1.6761 | Data_field |
| 5 | 1.6761 | Data_feild_code |
| 6 | 0 | Time_period |
| 7 | 0 | Time_period_type |
| 8 | 1.074 | value |
| 9 | 0 | Unit |
Table 3: Attribute ranking.
Clustering using GMM in spark environment
A Gaussian mixture model is a probabilistic model that takes all the data points that are generated from a mixture of a finite number of Gaussian distributions with unknown parameters and cluster them by calculating the parameters values. Gaussian mixture model clustering is implemented on the reduced Zika virus dataset. The input dataset is of the ‘csv’ format. The number of Gaussians is predefined by the user. The Algorithm can be run again with a different number of cluster values. The Gaussian mixture object implements the expectation maximization (EM) algorithm for fitting the mixture of Gaussian models. Re-estimation of the parameters is done using machine learning library of spark till the changes in parameters values becomes very low. The weight of the Gaussian is calculated by the number of records it holds. Higher weight of the Gaussian signifies that it contains more records.

Results
Clustering in Zika virus dataset is performed using Gaussian mixture model to group entities based on the similarities among them. The clustering is performed for a different number of clusters or Gaussians with values of k=2, 3, 4. The multiple runs of the algorithm may produce different Gaussians with slightly different parameters. This is due to the machine learning concepts involved for calculating the parameters of the Gaussians using the probability. The final result is tabulated below.
Determining the number of clusters is tricky. If the number of clusters is more, size of the clusters will be smaller, therefore error will be smaller. But if we keep on increasing the number of clusters, at some point, k would become equal to (total data points), which means each cluster will have one data point, which will be meaningless as it would not provide any insight.
On increasing the number of clusters, the difference between the results become less significant. Therefore, we can stop at the point, where the results difference is significant enough, to gather some extra knowledge. The authors decided to use clusters, where k=2, 3, and 4.
In Table 4, the number of clusters taken is, k=2, the mean and sigma values for different attributes for the particular Gaussian are given. ‘wt’ represents the weight of the Gaussian. The higher weight of the Gaussian represents more number of records. With k=2, Gaussian 1 has a higher weight of 71%, which means it contains 71% of the total number of records, i.e., 1393. The mean values, using Table 2, corresponds to “report_date=13-04-2016”, “Location=United States Indiana”, “Location_type=state”, and “Data_feild=Zika reported travel” in the dataset.
| Attributes | Gaussian 1 (wt=0.710848) | Gaussian 2 (wt=0.289151) | ||||
|---|---|---|---|---|---|---|
| Mean (μ) | σ1 | σ2 | Mean (μ) | σ1 | σ2 | |
| report date | 1.3071 | 0.004151 | 0.001894 | 1.3038 | 5.95565E-4 | 1.9206E-14 |
| Location | 2.3483 | 0.042266 | 0.006693 | 2.0157 | 0.002162 | 3.9543E-14 |
| Location type | 3.1807 | 0.006693 | 0.002838 | 3.2999 | 3.9543E-14 | 8.5865E-14 |
| Data field | 4.2139 | 0.002571 | 0.001126 | 4.1127 | 6.12739E-4 | 9.0384E-14 |
| Value | 21.04199 | 0.880576 | 0.765795 | 33.0607 | 5.121991 | 3.9769E-13 |
Table 4: Number of clusters (k)=2.
Similarly, Table 5 represents the clustering when the number of Gaussians are k=3. Gaussian 1 contains a weight of 23.6%, Gaussian 2 contains weight of 55.2% while Gaussian 3 contains a weight of 21%. The corresponding mean and sigma values of all the Gaussians are provided in the table.
| Attributes | Gaussian 1 (wt=0.236589) | Gaussian 2 (wt=0.552567) | Gaussian 3 (wt=0.210842) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean (μ ) | σ1 | σ2 | Mean (μ ) | σ1 | σ2 | Mean (μ) | σ1 | σ2 | |
| Report date | 1.3011 | 2.157E-4 | 3.077E-4 | 1.3032 | 0.00516 | 0.00249 | 1.3196 | 0.00218 | -6.99E-4 |
| Location | 2.0113 | 6.873E-4 | -3.69E-5 | 2.3705 | 0.03200 | 0.00294 | 2.2122 | 0.06534 | 0.00934 |
| Location type | 3.2972 | -3.69E-5 | 5.649E-4 | 3.1796 | 0.00299 | 0.00163 | 3.2164 | 0.00934 | 0.00766 |
| Data field | 4.0924 | 1.745E-4 | -3.18E-4 | 4.2156 | 0.00208 | 0.00113 | 4.2070 | 0.00304 | 7.60E-4 |
| Value | 11.9271 | 2.22459 | -0.12981 | 7.4587 | 0.62007 | 0.24349 | 83.3509 | 6.21301 | 2.98593 |
Table 5: Number of clusters (k)=3.
Table 6 represents the clustering when the number of clusters are defined as k=4. Here Gaussian 1 contains a weight of 39.3%, Gaussian 2 contains a weight of 44.6%, Gaussian 3 contains a weight of 9.8% and Gaussian 4 contains a weight of 6.1%. The corresponding mean and sigma values are provided in the table.
| Attributes | Gaussian 1 (wt=0.393252) | Gaussian 2 (wt=0.446924) | ||||
| Mean (μ ) | σ1 | σ2 | Mean (μ ) | σ1 | σ2 | |
| Report date | 1.27198 | -0.00561 | 0.00352 | 1.33436 | 0.00100 | 3.947E-14 |
| Location | 2.07746 | 0.00997 | -0.00806 | 2.40781 | 0.03334 | 1.052E-13 |
| Location type | 3.22483 | -0.00806 | 0.00929 | 3.19999 | 1.052E-13 | 5.262E-14 |
| Data field | 4.12173 | 0.00268 | -0.00314 | 4.22999 | 6.724E-14 | 8.715E-15 |
| Value | 6.76576 | -0.14632 | 0.11691 | 6.87202 | 0.24860 | 4.838E-10 |
| Gaussian 3 (wt=0.09811) | Gaussian 4 (wt=0.061712) | |||||
| Mean (μ ) | σ1 | σ2 | Mean (μ ) | σ1 | σ2 | |
| Report date | 1.31984 | 0.005279 | 0.001885 | 1.29832 | 0.002051 | 0.001194 |
| Location | 2.32117 | 0.076094 | 0.022004 | 2.12898 | 0.046852 | -1.28818 |
| Location type | 3.20015 | 0.022004 | 0.007446 | 3.28830 | -1.2881E-4 | 0.00103 |
| Data field | 4.22125 | 0.001748 | 6.129E-4 | 4.19993 | 0.001475 | 4.66932 |
| Value | 51.2580 | -6.397953 | -2.322023 | 222.911 | 51.76236 | 1.82374 |
Table 6: Number of clusters (k)=4.
Report_Date: It is observed that for k=2, 3 the report date is same i.e. 1.30, which signifies that most of the cases were reported on the same day. While for k=4, other major days can be obtained.
Location: In the dataset, 70 distinct locations are present. While most of the cases are reported for location coded between 2.34 to 2.37. For k=4, other major locations can be obtained by using the mean and weight of the Gaussian.
Data_feild: It signifies, the type of case reported, data field coded as 4.21 was reported the most. For k=4, most types of cases can be found by corresponding mean and weight.
Conclusion
There was a widespread Epidemic of Zika virus in 2015 which was mainly spread by Aedes mosquitos. Due to its sudden emergence as a deadly human pathogen, it created a lot of chaos among the general people. One of the problems was to determine the intensity of spread of the virus with a large number of records. In this paper, the authors have presented the method for clustering of Zika virus epidemic using Gaussian mixture. The data complexity is reduced by using Entropy-based ranking. It calculates the Information gain from each attribute. Therefore by retaining the most significant data the authors increased the accuracy of the system and producing faster results.
Number of clusters (k) is the important criteria for the determining the accurate knowledge from the data. For k=2, Gaussians would not be able to provide much understanding. Increasing the number of clusters to k=3 and further to k=4, provide a much accurate insight from the data. As the number of clusters increases, the farther data points also contribute more to the information, thus deriving greater knowledge from the data. However, increasing the number of cluster further may not provide any significant difference in the result and will take more amounts of computation and other resources.
The Gaussian mixture model is the appropriate model of clustering for this study, as it is a type of soft clustering method, which considers mean, variance and weight of the clusters. Using this clustering method, the major locations, types and reported dates are found, which can be useful in understanding the spread of the virus. The program can work on any numeric type dataset, and form appropriate Gaussian clusters to provide some insight from the data. In future, the present study can be expanded to include the visualization of these clusters and the spread of the virus in the world during the epidemic in real time. Also this method can be used to analyse the spread of any other epidemic in the future.
References
- Zika Virus. http: //www.who.int/mediacentre/factsheets/zika/en/
- David S, Jia G, Gagan A. Smart-MLlib: a high-performance machine-learning library. IEEE International Conference on Cluster Computing (CLUSTER) 2016; 336-345.
- Revlin A, Elia ED, Christos V, Peter M. A Gaussian mixture model approach to grouping patients according to their hospital length of stay. 21st IEEE International Symposium 2008; 524-529.
- Kart-Leong L, Han W. Learning a field of Gaussian mixture model for image classification. 14th International Conference on Control, Automation, Robotics and Vision (ICARCV) 2016; 1-5.
- Arindam D, Owen M, Meynard T, Matthew PB, Daniel WB. Comparing Gaussian mixture model and hidden Markov model to classify unique physical activities from accelerometer sensor data. 15th IEEE International Conference on Machine Learning and Applications (ICMLA) 2016; 339-346.
- Pérez JF, Gómez A, Giraldo JH, Guzmán S, Fernández DS. Automatic segmentation of coral reefs implementing textures analysis and color features with Gaussian mixtures models. 6th Latin-American Conference on Networked and Electronic Media (LACNEM) 2015; 1-6.
- Bei Z, Yanfei Z, Ailong M, Liangpei Z, A spatial Gaussian mixture model for optical remote sensing image clustering. IEEE J Select Top Appl Earth Observ Remote Sens 2016; 9: 5748-5759.
- Heng-Chao Y, Jun-Hong Z, Chee Khiang P. Gaussian mixture model using semisupervised learning for probabilistic fault diagnosis under new data categories. IEEE Trans Instrument Measur 2017; 66: 723-733.
- Gaussian Mixture Model. http: //scikit-learn.org/stable/modules/ mixture.html.
- Spark. http: //spark.apache.org/