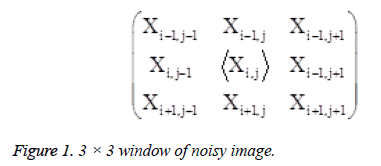Research Article - Biomedical Research (2017) Volume 28, Issue 2
An enhanced algorithm for removal of noise in CT scan image and 3D abdomen color video sequence through trimmed based filter
G Elaiyaraja1* and N Kumaratharan21Department of ECE, Adhiparasakthi College of Engineering, Anna University Chennai, Tamilnadu, India
2Department of ECE, Srivenkateswara College of Engineering, Anna University Chennai, Tamilnadu, India
- *Corresponding Author:
- G Elaiyaraja
Department of ECE, Adhiparasakthi College of Engineering
Anna University, India
Accepted date: May 10, 2016
Abstract
In this paper, a new Trimmed Median (TM) filter to remove high density fixed impulse noise in CT (computerized tomography) scan images and abdomen color video sequence is proposed. Initially, a 3 × 3 sliding window is applied on each pixel in the noisy image and color video sequence frame. The minimum and maximum intensity values are trimmed and the noisy pixels are detected based on the predefined threshold value. In the filtering stage, the noisy pixels are replaced by median value of uncorrupted pixels in the trimmed array. At very high noise density, if all the pixels in the sliding window are corrupted then the proposed algorithm replaces noisy pixel by midpoint of recently processed pixels. The experimental results for noisy lung CT scan image show that the performance of proposed algorithm is superior to existing algorithms in terms of visual quality and edge preservation, even at noise level as high as 95%.
Keywords
CT scan image, Fixed value impulse noise, Non-linear filter, Trimmed median (TM) filter.
Introduction
Medical images and CT scan videos are often degraded by fixed value impulse noise due to malfunctioning of camera sensors, faulty memory locations in hardware and transmission of image in noisy channel which can seriously affect quality of the images [1].In this work we focus on the fixed valued impulse noise, which can take two extreme intensity values normally being the minimum (0) and maximum (255), contributing to white and blocks dots on image. In an image, edges contain essential information and the objective of any filtering technique is to remove the impulses so that the edge details should be preserved. Generally, linear filtering techniques for image restoration tend to blur the edges. The simplest nonlinear filter to remove the fixed value impulse noise is the Standard Median Filter (SMF) [2]. Median filters are widely used due to their efficient noise suppression capability. But at higher noise level they do not perform well. To overcome this problem, modified median filters such as Weighted Median Filter (WMF), Adaptive Center Weighted Median Filter (ACWMF) and Multistate Median Filter were introduced.
In order to overcome the problem of median based filters, different kinds of decision based median filters such as Progressive Switching Median Filter (PSMF) [3] and Adaptive Median Filter (AMF) [4] have been proposed. Since the AMF uses larger window size and PSMF uses several iterations to detect the presence of noise, their CPU time is also very high. In addition to that switching strategy used in certain switching based median filters cannot differentiate high frequency edges from high frequency impulses in a noisy image. Hence to recover edges satisfactorily by taking into account the local features, a switching median filter incorporated with powerful noise detection method called as Boundary Discriminative Noise Detection (BDND) was proposed [5]. In this algorithm two iterations are invoked to detect and validate the kind of current pixel as noisy or noise free. The pixels detected as noisy are then restored with NASSMF [6] filter. Though BDND filter provides accurate noise detection, it is time consuming due to more number of pixels are processed to detect the presence of noise.
In order to overcome complexity of the different switching based median filters, a new switching Decision Based Algorithm (DBA) is proposed [7] which use the fixed window with a size of 3 × 3 for image denoising. If the center pixel of the sliding window is either ‘0’ or ‘255’, it is replaced with median value otherwise retained. At higher noise level all the pixels in the selected window are corrupted, and the median value may also be a noisy value in which case the previously processed left neighborhood pixel is used to replace the corrupted center pixel which produces streaking effect. To address this issue, Decision Based Unsymmetric Trimmed Median Filter (DBUTMF) is proposed [8]. In this filter at higher noise level, the trimmed median value cannot be obtained if the selected window contains all the pixels as noisy pixels. In addition to that DBUTMF does not provide better restoration result at higher noise ratio. To overcome the above drawback the Modified Decision Based Unsymmetric Trimmed Median Filter (MDBUTMF) is proposed which takes the mean of all the pixels in a selected window to replace the noisy center pixel [9]. Since this filter detects the presence of salt and pepper noise by maximum intensity value ‘255’ and minimum intensity value ‘0’, the detection accuracy is not enough to restore the images corrupted with more than 80% of noise level. In addition to that if all the pixels in the window are either ‘0’ or ‘255’, then the MDBUTMF replaces the noisy pixel by mean value which is also either ‘0’ or ‘255’. Unlike the median filter, mean filter smoothen the images. Fast and efficient median filter (FEMF) uses prior information to get natural pixels for restoration. Without any iteration, it detects impulse noises intuitively, leaving the others unaltered. So it has very fast execution speed [10]. The Noise adaptive fuzzy switching median filter (NAFSMF) utilizes the histogram of the corrupted image to identify noise pixels and employs fuzzy reasoning to handle uncertainty present in the extracted local information as introduced by noise [11]. In the new filter proposed in [12], the corrupted pixels are replaced by using a median filter or estimated by their neighbors’ values.
In this paper a new decision based trimmed median filter to remove high density salt and pepper noise with improved qualitative and quantitative measures is proposed. A fixed 3 × 3 sliding window is applied on a center pixel being processed and pixels in the sliding window are sorted. The trimmed array is obtained by eliminating the minimum and maximum intensity values in a sorted array. The noisy pixels are detected by comparing the absolute difference between the center pixel and median value of uncorrupted pixels in the trimmed array with a predefined threshold value ‘T’. If it is identified as noisy pixel, then it is replaced with the median value otherwise left unaltered.We observed that the design of using trimmed median has been used to deal with other types of noise [13-15].
The rest of this paper is organized as follows. In Section II, the proposed trimmed median filtering algorithm is described and Illustration is given in section III. The simulation results of the proposed trimmed median filter in image and video denoising application and performance with other existing algorithms are demonstrated in section IV. The section V concludes the paper.
Proposed New Trimmed Median (Tm) Filter
In case of videos separate videos into frames .Now every frame will act as an image. Initially a 3 × 3 sliding window is imposed on each pixel being processed in the noisy image. The minimum intensity (Smin) and maximum intensity (Smax) values obtained in the selected window are trimmed and remaining pixels which are not equal to Smin and Smax are collected in an array. Then the absolute difference between center pixel and mean of those pixels collected in an array is compared with predefined threshold value ‘T’ to detect whether the center pixel is corrupted or not. If it is detected as noisy, then filtering is applied otherwise left unaltered. The proposed algorithm on images and videos is explained in the following steps.
Algorithm Steps:
Step 1: Choose 2-D window of size 3 × 3. Let Xij is a pixel being processed in the noisy image. The minimum (Smin) and maximum (Smax) intensity values in the window are obtained by sorting the elements in the array Zi/i=1:9.
Figure 1 shows the processed pixels of image in which there are nine pixels. Assume that the current pixel ˂ Xi,j ˃ is the processed pixel for noise detection.
Unsorted Array Zi/i-19=[Xi-1,j-1,Xi,j-1,Xi+1,j-1,Xi-1,j,Xi,j,Xi +1,j,Xi-1,j+1,Xi-1,j+1,Xi+1,j+1] Sorted Array
sort(Zi)=[X0,X1,X2,X3,X4,X225,X225,X225] Where X0 and X255 are 0’s and 255’s pixels of processed image i.e., Smin=X0 and Smax=X255
Case (i)
Step 2: If the minimum intensity value Smin=0 and maximum intensity value Smax=255 continue, else go to step 6.
Step 3: The Smin and Smax values in the array Zi are trimmed and all the uncorrupted pixels which are not equal to Smin and Smax are retained in the same array. If ‘Zi’ is empty go to step 11, else continue.
Trimmed array
Trim(Zi)=[X1,X2,X3,X4]
Step 4: Median (MED) of an array Zi is found.
Median Value (MED)=Med (Trim (Zi))
If |Xij-MED| < T then Xij is noise free and actual value is retained otherwise Xij is replaced with MED, where the threshold value ‘T’ lies in the range [16-19]. Thus noise Detection can be expressed as
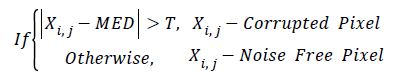
The Noise Pixel Replacing Process can be expressed as
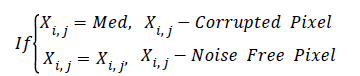
Step 5: Repeat the process from step 1, till all the pixels in the noisy image are processed.
Case (ii)
Step 6: If the minimum intensity value Smin=0 and maximum intensity value Smax ≠ 255 continue, else go to step 8.
Sorted Array
sort(Zi)=[X0,X0,X0,X1,X2,X3,X4,X5,X6]
Step 7: The Smin and Smax values in the array Zi are trimmed and all the uncorrupted pixels which are not equal to Smin in trimmed array Zi are retained. If Zi’ is empty go to step 11, else go to step 4.
Trimmed array
Trim(Zi)=[X1,X2,X3,X4,X5,X6]
Case (iii)
Step 8: If the minimum intensity value Smin ≠ 0 and maximum intensity value Smax=255 continue, else go to step 11.
Sorted Array
Step 9: The Smin and Smax values in the array Zi are trimmed and all the uncorrupted pixels which are not equal to Smax in trimmed array Zi are retained. If ‘Zi’ is empty go to step 11, else go to step 4.
Trim(Zi)=[X1,X2,X3,X4,X5,X6]
Step 10: The current processing pixel Xij is noise free and actual value is retained. This is illustrated in case (iv) of section III.
Step 11: The midpoint of previously processed neighbors of Xi-1,j, Xi,j-1 is used to replace the center pixel Xij and go to step 5.
The optimum threshold value ‘T’ is determined by trial and error approach for various test images and lies approximately in the range [16-19].
Illustration of Proposed Filter
This section illustrates the proposed algorithm with four different cases for lung CT scan image corrupted with 90% of salt and pepper noise.
Case (i)
If the center pixel in selected window is noisy and some neighborhood pixels add salt and pepper noise to the image is illustrated in case (i). The pixels in selected window are sorted and minimum (Smin) and maximum (Smax) intensity values are trimmed. Then the uncorrupted pixels which are not equal to Smin and Smax in Zi are retained. The median value of the array Zi is found. Since the absolute difference between the median value and center pixel value is greater than 30, the center pixel is noisy and replaced with median value as shown below.
Unsorted array Zi= [0, 0, 46, 49, 255, 255, 50, 255, 48]
Sorted array Zi= [0, 0, 46, 48, 49, 50,255,255,255]
Trimmed array Zi= [46, 48, 49, 50]
Median=49
|Xij-Med|=206>30, Xij=49
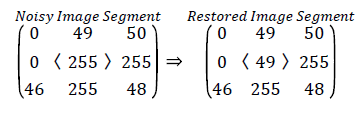
Case (ii)
If the center pixel in selected window is noisy and some neighborhood pixels add pepper noise to the image is illustrated in case (ii). Since the absolute difference between the median value of the array Zi and center pixel value is greater than 30, the center pixel is noisy and replaced with median value.
Unsorted array Zi= [0, 205, 0, 205, 0, 208, 206, 209, 205]
Sorted array Zi= [0, 0, 0,205,205,205,206,208,209]
Trimmed array Zi= [205,205,205,206,208]
Median=205
|Xij-Med|=205>30, Xij=205
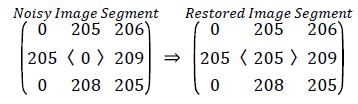
If the center pixel in selected window is noisy and some neighborhood pixels add salt noise to the image is illustrated in case (iii). Since the absolute difference between the median value of the array Zi and center pixel value is greater than 30, the center pixel is noisy and replaced with median value.
Unsorted array Zi= [255, 51, 52, 49, 255, 255, 57, 50, 48]
Sorted array Zi= [48, 49, 50, 51, 52, 57,255,255,255]
Trimmed array Zi= [49, 50, 51, 52, 57]
Med=51
|Xij-Med|=204>30, Xij=51
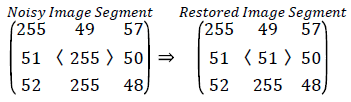
Case (iv)
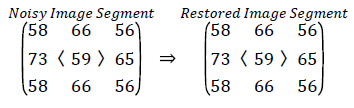
If the center pixel is noise free, then the absolute difference between the median value and center pixel is less than 30, then the processing pixel is left unaltered.
Unsorted array Zi= [58, 73, 58, 66, 59, 66, 56, 65, 56]
Sorted array Zi= [56, 56, 58, 58, 59, 65, 66, 66, 73]
Med=59
|Xij-Med|=0<30, Xij=59
Results and Discussion
In this section, performance of the proposed filter is tested by using lung CT scan image of size 512 × 512, 8 bits/pixel and compared with existing algorithms like PSMF, AMF, ACWMF, BDND, DBA, FEMF and MDBUTMF by varying the noise level from 10% to 90% with the incremental step of 10% for every simulation. In addition to the visual quality, the performance of the proposed algorithm and other existing algorithms are quantitatively measured by the parameters such as Peak Signal-to-Noise Ratio (PSNR), Mean Absolute Error (MAE), Structural Similarity Index (SSIM) and Image Enhancement Factor (IEF). The performance of restoration and processing time for proposed filter and existing filters are analyzed under the following sections A and B.
Quantitative and visual results comparison
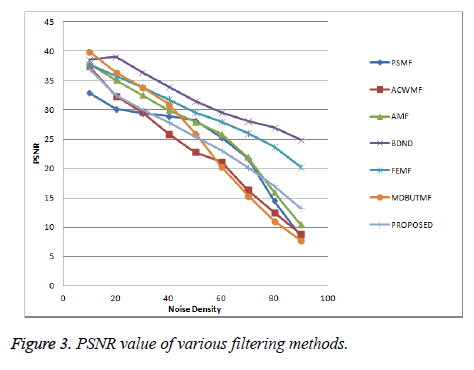
The restoration performance of the proposed algorithm is demonstrated in this section. The quantitative performance metrics in terms of PSNR, MAE, IEF and SSIM for proposed filter and seven competitive filters for the Lung CT scan image at noise level varying from 10% to 90% are documented in Tables 1-4. It can be seen from the table that the PSNR value obtained in PSMF algorithm is very low compared to proposed filter for all noise densities.
| Noise Density |
PS MF |
AC WMF |
AMF | BD ND |
DBA | FEMF | MDB UTMF |
Proposed |
|---|---|---|---|---|---|---|---|---|
| 10 | 32.90 | 37.37 | 37.86 | 38.55 | 37.79 | 39.91 | 36.95 | 39.26 |
| 20 | 30.18 | 32.37 | 35.09 | 39.05 | 35.73 | 36.45 | 32.53 | 37.27 |
| 30 | 29.45 | 29.62 | 32.54 | 36.38 | 33.89 | 33.84 | 30.04 | 35.67 |
| 40 | 28.94 | 25.87 | 29.99 | 33.94 | 31.81 | 30.98 | 27.88 | 34.47 |
| 50 | 28.23 | 22.81 | 27.97 | 31.49 | 29.61 | 26.02 | 25.49 | 33.11 |
| 60 | 25.32 | 21.17 | 25.90 | 29.62 | 27.97 | 20.32 | 23.09 | 31.51 |
| 70 | 21.76 | 16.33 | 21.95 | 28.09 | 26.08 | 15.41 | 20.17 | 29.73 |
| 80 | 14.52 | 12.52 | 15.96 | 27.07 | 23.67 | 11.11 | 17.06 | 27.74 |
| 90 | 8.52 | 8.85 | 10.47 | 24.91 | 20.27 | 7.8 | 13.26 | 24.48 |
Table 1: PSNR comparison for lung CT scan image.
| Noise Density |
PS MF |
AC WMF |
AMF | BD ND |
DBA | FEMF | MDB UTMF |
Proposed |
|---|---|---|---|---|---|---|---|---|
| 10 | 0.90 | 0.56 | 0.97 | 0.36 | 0.97 | 0.45 | 0.65 | 0.25 |
| 20 | 1.69 | 1.22 | 1.30 | 0.76 | 1.29 | 0.95 | 1.38 | 0.45 |
| 30 | 2.25 | 2.17 | 1.80 | 1.24 | 1.75 | 1.55 | 2.21 | 0.66 |
| 40 | 2.57 | 3.48 | 2.49 | 1.79 | 2.37 | 2.27 | 3.40 | 0.87 |
| 50 | 3.11 | 5.52 | 3.35 | 2.59 | 3.16 | 3.67 | 4.85 | 1.13 |
| 60 | 4.12 | 9.17 | 4.49 | 3.51 | 4.15 | 7.28 | 7.16 | 1.46 |
| 70 | 6.94 | 16.1 | 6.97 | 4.47 | 5.59 | 16.8 | 11.2 | 1.86 |
| 80 | 20.50 | 30.5 | 15.8 | 5.50 | 7.65 | 37.0 | 18.2 | 2.50 |
| 90 | 66.06 | 65.2 | 43.8 | 7.03 | 12.5 | 75.4 | 37.0 | 3.90 |
Table 2: MAE comparison for lung CT scan image.
| Noise Density |
PS MF |
AC WMF |
AMF | BD ND |
DBA | FEMF | MDB UT MF |
Proposed |
|---|---|---|---|---|---|---|---|---|
| 10 | 256.9 | 96.42 | 197.5 | 234.6 | 234.1 | 469.1 | 126.6 | 672.2 |
| 20 | 310.1 | 46.64 | 151.5 | 155.7 | 416.3 | 597.4 | 115.7 | 761.9 |
| 30 | 375.3 | 33.79 | 109.6 | 124.2 | 547.2 | 453.3 | 94.62 | 760.9 |
| 40 | 478.7 | 23.41 | 45.08 | 113.2 | 637.0 | 440.4 | 67.75 | 733.2 |
| 50 | 474.2 | 19.11 | 34.04 | 77.67 | 545.3 | 233.0 | 52.67 | 687.3 |
| 60 | 389.5 | 11.35 | 25.67 | 59.41 | 404.3 | 63.59 | 33.03 | 625.3 |
| 70 | 128.6 | 7.30 | 15.86 | 51.37 | 191.3 | 18.61 | 20.05 | 519.0 |
| 80 | 12.6 | 5.14 | 9.62 | 40.76 | 74.93 | 5.24 | 11.15 | 422.6 |
| 90 | 1.32 | 1.66 | 3.20 | 32.84 | 17.52 | 1.72 | 4.89 | 272.7 |
Table 3: IEF comparison for lung CT scan image.
| Noise Density | PS MF | AC WMF | AMF | BD ND | DBA | FEMF | MDB UTMF | Proposed |
|---|---|---|---|---|---|---|---|---|
| 10 | 0.912 | 0.982 | 0.963 | 0.990 | 0.963 | 0.986 | 0.983 | 0.99 |
| 20 | 0.880 | 0.958 | 0.955 | 0.979 | 0.954 | 0.970 | 0.961 | 0.98 |
| 30 | 0.883 | 0.921 | 0.939 | 0.963 | 0.938 | 0.950 | 0.931 | 0.96 |
| 40 | 0.903 | 0.855 | 0.917 | 0.945 | 0.915 | 0.919 | 0.884 | 0.95 |
| 50 | 0.903 | 0.757 | 0.888 | 0.915 | 0.883 | 0.828 | 0.828 | 0.93 |
| 60 | 0.874 | 0.604 | 0.840 | 0.878 | 0.840 | 0.608 | 0.722 | 0.90 |
| 70 | 0.777 | 0.414 | 0.714 | 0.841 | 0.779 | 0.296 | 0.561 | 0.88 |
| 80 | 0.456 | 0.207 | 0.397 | 0.800 | 0.697 | 0.098 | 0.368 | 0.83 |
| 90 | 0.095 | 0.059 | 0.087 | 0.741 | 0.542 | 0.024 | 0.153 | 0.76 |
Table 4: SSIM comparison for lung CT scan image.
The simulation results for the Lung CT scan image displayed in Table 1 show that the PSNR value provided by the algorithms ACWMF, AMF, DBA and MDBUTMF are equally better to proposed algorithm for noise level up to 30% and decays to very low value at high noise ratio. The algorithm DBA has also given the lower PSNR value than proposed filter for noise level more than 50%. The BDND algorithm exhibits equally good PSNR value as obtained in proposed algorithm due to processing of more number of pixels in two iterations, but it leads to blurring effect in an output image for high noise density. Hence it is easy to see that, proposed filter provides better PSNR value than existing filters, for the images with low edge details like Lung CT scan image. Similarly Tables 2 and 3 also show that, the mean absolute error obtained for the proposed algorithm is much lower than other existing algorithms at higher noise level which leads to better image enhance factor. The proposed algorithm also exhibits improved structural similarity index which is displayed in Table 4. The PSNR quantitative performance comparison is also presented graphically in Figure 3.
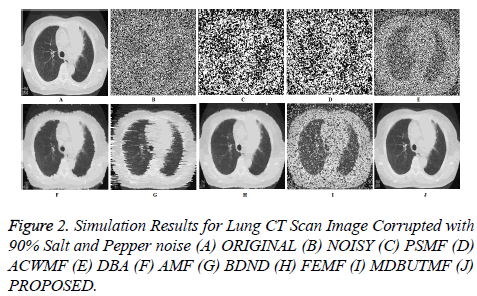
The proposed algorithm is analyzed qualitatively by observing the restoration result of proposed algorithm and existing algorithms visually, for the lung CT scan image corrupted with 90% of salt and pepper noise is shown in Figure 2B. The algorithms PSMF, ACWMF, FEMF and MDBUTMF leave some noticeable impulses in the denoised output image. In the algorithm DBA streaking effect dominates due to the replacement of noisy pixel by restored left neighborhood when all the pixels in the sliding are corrupted. The filters BDND and AMF restore the original image with slight blurring, because of larger window size. The Figures 2C-2J show the restoration results of various filters for the lung CT scan image corrupted with 90% salt and pepper noise. Based on subjective visual comparisons, it is also observed that proposed filter removes impulse noise effectively and preserve the image details such as edges better than other existing filters. The error image for proposed filter looks darker than other competitive filters which mean that it gives better restoration at higher noise level. Based on the above analysis it is easy to see that the proposed filter outperforms the existing switching based filters in both quantitative and qualitative aspects. A graph of PSNR value of various filtering methods as shown in Figure 2. It is show that proposed filter PSNR value is higher than other filtering methods.
Run time comparison
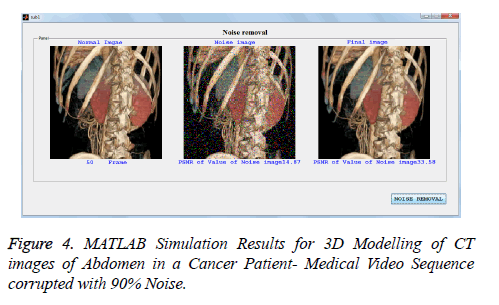
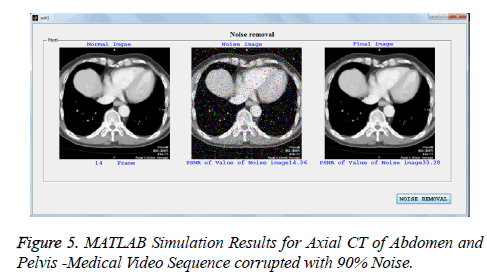
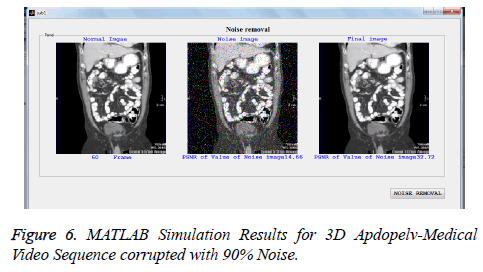
In addition to PSNR, MAE, and MSSIM, the performance of proposed filter is also tested quantitatively in terms of processing time and compared with existing filters for lung CT scan image with noise level varying from 10% to 90% and listed in Tables 5. All the filters are simulated in MATLAB in PC equipped with 2.66 GHZ operating speed, 2 GB RAM. From the table it is observed that PSMF and BDND algorithms have taken longer run time than proposed, since they process more number of pixels in an iterative manner. The AMF is also executed with longer time than proposed filter especially at higher noise densities, since it uses large window size for higher noise ratio. The run time for ACWMF and MDBUTMF is lesser, only at lower noise level and they are executed with run time almost closer to proposed filter. The fixed window algorithms DBA and FEMF algorithms have taken the run time much closer to the proposed filter for noise level varying from 10% to 90%, but other performance metrics are not satisfied. Hence the proposed filter provides better trade off among runtime and other performance metrics such as PSNR and visual quality than existing algorithms especially at higher noise level. The MATLAB simulations results of proposed algorithm for color medical 3D videos sequence as shown in Figures 4-6 [20]. It shows that proposed filter is better video noise removal for color and gray level video sequence.
| Noise Density | PS MF | AC WMF | AMF | BD ND | DBA | FEMF | MDB UTMF | Proposed |
|---|---|---|---|---|---|---|---|---|
| 10 | 38.92 | 2.12 | 6.91 | 23.95 | 6.54 | 5.21 | 2.23 | 7.44 |
| 20 | 37.14 | 2.79 | 7.01 | 24.78 | 6.51 | 5.43 | 2.79 | 7.45 |
| 30 | 36.78 | 3.33 | 7.11 | 25.92 | 6.56 | 5.65 | 3.31 | 7.48 |
| 40 | 36.75 | 3.92 | 7.34 | 27.28 | 6.54 | 5.84 | 3.93 | 7.49 |
| 50 | 36.65 | 4.52 | 7.98 | 29.75 | 6.54 | 6.14 | 4.58 | 7.51 |
| 60 | 36.91 | 5.09 | 8.62 | 32.64 | 6.54 | 6.21 | 5.09 | 7.51 |
| 70 | 36.93 | 5.71 | 10.0 | 34.79 | 6.53 | 6.41 | 5.71 | 7.48 |
| 80 | 37.43 | 6.22 | 12.5 | 36.32 | 6.53 | 6.71 | 6.27 | 7.48 |
| 90 | 38.73 | 6.86 | 16.3 | 38.46 | 6.56 | 6.82 | 6.82 | 7.37 |
Table 5: Run time comparison for lung CT scan image.
Conclusion
In this work, a new decision based trimmed median filter with fixed window for effective removal of high density salt and pepper noise in images and videos is presented. The use of a small 3 × 3 fixed window in proposed algorithm leads to preservation of fine details such as edges satisfactorily. The good performance of proposed algorithm is due to the efficient noise detection achieved by comparing the absolute difference between center pixel and median value of the uncorrupted pixels in the sliding window with the predefined threshold value and efficient filtering achieved by replacement of noisy value by median of uncorrupted pixels in trimmed array. Simulation results reveals that the proposed filter outperforms the existing state of art filters by providing better PSNR, IEF, SSIM, MAE values and visual quality for the images corrupted up to 95% of noise level.
References
- Bovik C. Handbook of Image and Video Processing. New York, NY, USA: Academic, 2000.
- Huang TS, Yang GJ, Tang GY. Fast two-dimensional median filtering algorithm. IEEE Trans Acoust Speech Signal Process 1979; 27: 13-18.
- Wang Z, Zhang D. Progressive switching median filter for the removal of impulse noise from highly corrupted images. IEEE Trans Circuits Syst II: Analog Digital Signal Process 1999; 46: 78-80.
- Hwang H, Haddad RA. Adaptive median filters: New algorithms and results. IEEE Trans Image Process 1995; 4: 499-502.
- Ng PE, Ma KK. A switching median filter with boundary discriminative noise detection for extremely corrupted images. IEEE Trans Image Process 2006; 15: 1506-1516.
- Eng HL, Ma KK. Noise adaptive soft-switching median filter. IEEE Trans Image Process 2001; 10: 242-251.
- Jayaraj V, Ebenezer D. A new switching-based median filtering scheme and algorithm for removal of high-density salt and pepper noise in image. EURASIP J Adv Signal Process 2010.
- Aiswarya K, Jayaraj V, Ebenezer D. A new and efficient algorithm for the removal of high density salt and pepper noise in images and videos. in Second International Conference on Computer Modeling and Simulation, 2010, 409-413.
- Esakkirajan S, Veerakumar T, Subramanyam AN, PremChand CH. Removal of High Density Salt and Pepper Noise Through Modified Decision Based Unsymmetric Trimmed Median Filter. IEEE Signal processing Letters 2011; 18: 287-290.
- Hsieh MH, Cheng FC, Shie MC, Ruan SJ. Fast and efficient median filter for removing 1-99% levels of salt-and-pepper noise in images. Eng Applicat Artif Intell 2013; 26: 1333-1338.
- Toh KKV, Isa NAM. Noise adaptive fuzzy switching median filter for salt-and-pepper noise reduction. IEEE Signal Process Lett 2010; 17: 281-284.
- Jourabloo A, Feghahati AH, Jamzad M. New algorithms for recovering highly corrupted images with impulse noise. Sci Iranica 2012; 19: 1738-1745.
- Miao Z, Jiang X. Further properties and a fast realization of the iterative truncated arithmetic mean filter. IEEE Trans Circuits Systems II Exp Briefs 2012; 59: 810-814.
- Miao Z, Jiang X. Weighted iterative truncated mean filter. IEEE Trans Signal Process 2013; 61: 4149-4160.
- Miao Z, Jiang X. Additive and exclusive noise suppression by iterative trimmed and truncated mean algorithm. Signal Process 2013; 99: 147-158.
- Chen T, Wu HR. Space variant median filters for the restoration of impulse noise corrupted images. IEEE Trans Circuits Syst II: Analog Digital Signal Process 2001; 48: 784-789.
- Zhang S, Karim MA. A new impulse detector for switching median filters. IEEE Signal Process Lett 2002; 9: 360-363.
- Chan RH, Ho CW, Nikolova M. Salt-and-pepper noise removal by median-type noise detectors and detail-preserving regularization. IEEE Trans Image Process 2005; 10: 1479-1485.
- Luo W. Efficient removal of impulse noise from digital images. IEEE Trans Consum Electron 2006; 52: 523-527.
- Jiang X. Iterative truncated arithmetic mean filter and its properties. IEEE Trans Image Process 2012; 21: 1537-1547.