Research Article - Biomedical Research (2018) Medical Diagnosis and Study of Biomedical Imaging Systems and Applications
A symmetric medical image encryption scheme based on irrational numbers
Ranjith Kumar M1* and Viswanath MK2
1Research and Development Centre, Bharathiar University, Coimbatore-641046, Tamil Nadu, India
2Department of Mathematics, Rajalakshmi Engineering College, Thandalam, Chennai-602105, Tamil Nadu, India
- *Corresponding Author:
- Ranjith Kumar M
Research and Development Centre
Bharathiar University
Tamil Nadu, India
Accepted date: July 27, 2017
DOI: 10.4066/biomedicalresearch.29-17-1317
Visit for more related articles at Biomedical ResearchAbstract
In this paper, a new encryption scheme based on irrational numbers is implemented for the security of medical images in health information systems. It is a mutually authenticated scheme which is secure against all known standard attacks. The main feature of this scheme is that it is robust and the key is dynamic for each image transmission. This new scheme employs the linear transformation to shuffle the positions of image-pixels and uses the XOR-mod operation to confuse the relationship between the plainimage and cipher-image. The theoretical and statistical tests are carried out with detailed examinations, demonstrating the high level security of the new scheme.
Keywords
Fermat’s two square theorems, Moore-Penrose inverse, XOR mod operation, Irrational number
Introduction
The field of cryptography and its applications has grown rapidly during the past two decades with the advent of medical, military, industry communication and personal multimedia. Billions of images are transmitted through public channel every day. Depending on the application domain, it is necessary to prevent these images reaching unauthorized persons and this has become a big challenge. Due to some inherent features of images, such as high correlation among pixels and bulk data capacity, traditional encryption protocols [1-3] like AES, DES, RSA and Discrete-Log are not suitable for practical image encryption. The main drawback in designing the algorithm is that it is rather difficult to shuffle and diffuse by traditional means of cryptography. To meet this challenge, we develop a symmetric image transmission scheme based on irrational numbers.
As digital images are usually represented by two dimensional arrays, in order to fast-track de-correlate relations among pixels, we design a higher dimensional encryption key using the decimal expansion of an irrational number and then use it to shuffle the position of pixels in the secret image. We make use of our work [4] and the theorem of Fermat [5] in creating the keys for encrypting the plain-image. Meanwhile, to confuse the relationship between cipher-image and plain-image, a diffusion process among pixels is performed by XOR-mod operation. For instance, classical image encryption/decryption protocols [6] are very sensitive to keys, while chaotic maps [7,8] are sensitive to initial conditions and parameters. Also, the key had to be transmitted for encryption each time. We demonstrate in this paper how the above capabilities are incorporated in the communication system developed here using the broad idea of image encryption. Few advantages of this paper are the capacity to handle a large number of encryption keys to resist brute-force attacks, to encrypt the images securely with shuffle and diffusion properties on the respective decrypted images and in the use of keys which are dynamic in each encryption. This encryption algorithm is robust and efficient for encrypting medical images in medical image security realm and the transmission of cipher images in military image communications.
The New Encryption Scheme
The main object of this paper is to develop a mutually authenticated image transmission protocol that provides confidentiality, integrity and authenticity of the images shared over a public channel. This novel method of communication uses Fermat’s two squares theorem and the decimal expansion of an irrational number and is found to be fast and secure against standard attacks.
In this scheme, the transformation key matrix is constructed by an external secret key obtained from Fermat’s theorem and its entries are chosen from the billions of decimal places in the expansion of an irrational number. This matrix is used to distort the pixel co-ordinates of the plain-image. Meanwhile, to confuse the relationship between cipher-image and plain-image pixels, a diffusion process among pixels are performed using the XOR operation.
Initial setup
As before, assume that the two protagonists are Alice and Bob. An authentication protocol is executed by Bob to make sure that Alice wants to send him a confidential digital image.
Bob chooses a large number N at random and after ascertaining Alice’s identity sends it over a secure channel say, N is sent to Alice by Bob using the generalized Diffie-Hellman key exchange protocol [1,3]. Alice then finds the smallest prime N1 of the form 4t+1 greater than N. We recall the Fermat’s two squares theorem [5], “If p=4n+1 is prime in N then p=a2+b2 for some a,b ϵ N”. We exploit this theorem, to obtain the pair of numbers (A,B) when the prime N1 is known and N1=A2+B2. For example, if N1=28813=4(7203)+1, then 28813=932+1422.
Fermat’s theorem guarantee the existence of the numbers A and B from the sufficiently large N1. Note that, one of the two numbers A and B is odd, and the other is even as N1 is an odd number. Let A be odd, and B be even. Now, Alice owns the keys A and B once she is aware of N. Bob can also compute the keys A and B as he is aware of N1. For sending a second image Alice chooses the prime number of the form 4n+1, succeeding N1 and the process can be repeated as primes of the form 4n+1 are infinite.
Alice obtains the rectangular matrix R of order r × s using the number A and the entries of R are the (r.s) consecutive decimal places picked from the position A in the expansion of an irrational number I. Both the users agree for an irrational number I which has a decimal expansion upto more than million places of decimals, I is kept secret. It can be easily verified that rank(R)=s by actual computation as r is assumed to be greater than s. By Moore-Penrose properties [4,9,10], rank(RT.R)=rank(R)=rank(RT), that is rank(RT.R)=s and hence (RT.R) is non-singular. In particular (RT.R) is a 3 × 3 invertible matrix if s=3. Finally, Alice constructs the encryption key K as follows:
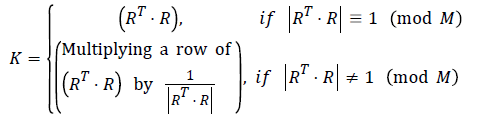
where K is a square matrix of order s × s, and clearly |K| ≡ 1 (mod M), which means that the transformation map is one-toone and area-preserving.
Encryption process
First Alice pile up the two dimensional plain-image into three dimensional image. Suppose that the image to be encrypted is of W × H pixels. First, one needs to pile up all pixels of the image, to form several cubes of size M1 × M1 × M2, M2 ×M2 × M2, …, Mi ×Mi × Mi respectively. To convert an image into several cubes, the following condition must be satisfied.
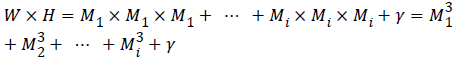
where Mi ϵ {2,3,..,M} the side length of each is cube, γ ϵ {1,2, …,7} is the remainder and M is the size of the maximum allowable cube.
Now, Alice applies the encryption key K on each cube and obtains the distorted images by the following linear transformation [11,12].
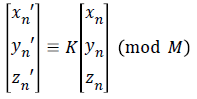
where (xn,yn,zn) the pixel is position in the corresponding cube; (xnʹ, ynʹ, znʹ) is the transformed position after the encryption. The process is continued till all the pixels on the plain-image are scrambled. Then Alice performs the diffusion process on the distorted-scrambled image, as follows.
Diffusion process
For a secure image encryption scheme, a diffusion algorithm is needed. It can significantly improve the statistical properties of the plain-image by spreading the influence of each bit of the secret image all over the cipher image.
For the purpose of diffusion, Alice applies the other secret key B XOR-mod operation on each pixel in the distorted image. Thus Alice computes the diffusion-image D by
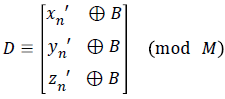
The three dimensional cubes can appropriately be arranged, laying back to a two dimensional image for display and Alice sends the key (r.s) along with the encrypted image to Bob for decryption.
The decryption procedure is similar to that of the encryption process illustrated above, with reverse operational sequences. Note that the square matrix K is always invertible. By this stratagem, Bob and Alice can send images to each other in a secure manner.
Working of the System
Consider the case where the irrational number I=π and N=35700. Then the value of tuple (N1,A,B) is (35729,127,140). Alice finds the sequence of decimal places from the position A=127 and chooses (r.s)=15 consecutive decimals from this position in the expansion of π. In this case, the sequence is: “60955058231725” and this is arranged in the form of a 5 × 3 rectangular matrix. Note that the rank(R)=3. Then (RT.R) is non-singular and
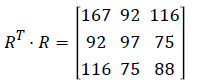
Here det(RT.R)=36873, gcd(36873, 64)=1 and 36873-1 ≡ 57(mod 64). Alice obtains the encryption matrix K, by multiplying the first row of the matrix (RT.R) with the number 57 such that det(K) ≡ 1(mod 64) and hence
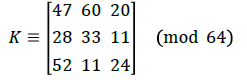
For the 512 × 512 plain-image, according to the encryption protocol, it will be piled upto a 64 × 64 × 64 cube. Now each pixels in the 3-dimensional image are encrypted by K. Suppose the pixel value (xn,yn,zn) is (47,3,62) then the distorted pixel value is
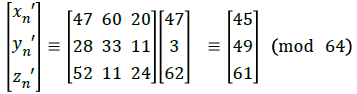
Alice further extends the encryption process by XOR-ing the distorted image pixels with the key B=140. Thus Alice computes the diffusion-image,
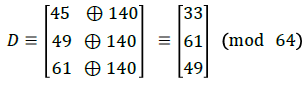
By performing this diffusion operation XOR-plus with B=140 to each pixel as above, then she appropriately arranges the three-dimensional cube laying back to a two-dimensional image. This cipher-image is dispatched to Bob along with the key (r.s)=15 for decryption.
Figure 1 shows the test results among the different images. On receiving the cipher-image, Bob performs inverse XOR-plus- B=140 pixels confusion, then applies the inverse linear transformation using
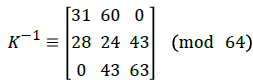 to obtain the original preimage:
to obtain the original preimage: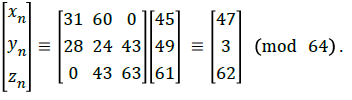
Security Analysis
Key scheme analysis
In this encryption protocol, the keys are dynamic and unlimited. It is impossible for the intruder to break the system by means of an exhaustive searching for the possible choices from the billion decimal places of an irrational number. The system is quite secure as it is difficult to obtain the key K without the knowledge of N. As N1 changes for each encryption, the pair (A, B) changes and so the key K is dynamic. This encryption algorithm changes the image pixel values while changing the locations of all the image pixels. This ensures that the ciphered image data is not useful in the case of a chosen-plaintext attack. It also ensures the authenticity of the images transferred between the sender and the receiver.
Statistical analysis
To analyse the correlation degree between two horizontally, vertically and diagonally adjacent pixels in a scrambled image, the following method is adopted. First, randomly choose T(=500) couples of two adjacent pixels from an image. Then making use of the equations (1), (2) and (3), determine the correlation coefficient of each pair separately.
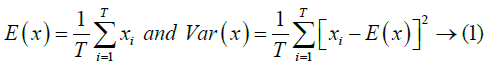
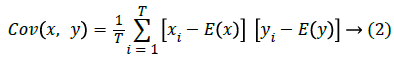
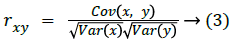
where x and y are values of two adjacent pixels in the image, E(x) is the mathematical expectation of x, Var(x) is the variance of x, Cov(x,y) is the covariance of x,y and rxy is the correlation coefficient of x,y.
Carrying out the experiment on the adjacent pixels of the plainimage and the cipher-image, the final value of the correlation coefficients is described in Table 1.
| Source of Variation | Correlation Coefficient of two adjacent pixels in the Plain-image | Correlation Coefficient of two adjacent pixels in the cipher-image |
|---|---|---|
| Horizontal | 0.9547 | 0.0082 |
| Vertical | 0.9353 | 0.0489 |
| Diagonal | 0.905 | 0.0093 |
Table 1. Correlation coefficients of two adjacent pixels in the plainimage and cipher-image.
From the table, we see that by comparing the ciphered image with the primitive plain-image along horizontal, vertical and diagonal directions, the correlation coefficients of the ciphered image are all much smaller. The purpose of scrambling is thus achieved and also shows that the scrambling degree of the algorithm is high. This experiment reveals the feasibility and effectiveness of the above algorithm.
Differential attack
This attack is one of the most famous attacks against an encrypted image. It is based on a slight change or modification of one pixel of the encrypted image by Eve, and then observes the corresponding change in the result. By this method Eve can find a relationship between the cipher-image and plain-image. So, if a minor change in the plain-image can cause a significant change in the cipher-image, then the differential attack would become practically useless [13-17].
The robustness of the proposed algorithm against the differential attack is analyzed by changing one pixel in the cipher image and by computing the values of NPCR and UACI, where NPCR and UACI denotes the Number of Pixel Change Rate and Unified Average Changing Intensity, respectively.
Denote two cipher-images, whose corresponding plain-images have only one-pixel difference, by C1 and C2, respectively. If C1(i,j) and C2(i,j) are the pixels at grid (i,j) of the cipherimages C1 and C2 respectively, then NPCR is defined by,
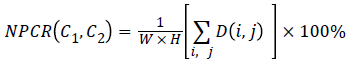
where W and H are the width and height of C1 or C2 and the bipolar array D(i,j) is determined from C1(i,j) and C2(i,j) as follows:
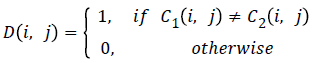
The NPCR value for two random D-bit images, namely the ideal value of the criterion, is given by:
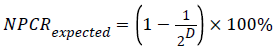
For instance, the expected NPCR for two random 8-bit grayscale images is 99.609%. The UACI measure the average intensity of differences between the plain-image and cipherimage, defined by:
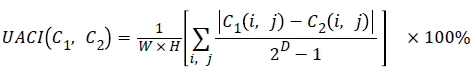
The UACI value for two random images is given by:
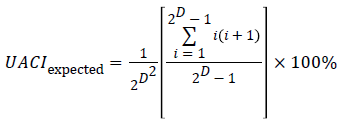
For an 8-bit grayscale image, the expected value of UACI is 33.464%.
By computing the values of NPCR and UACI in the case of the proposed encryption scheme we obtain, NPCR=99.24% and UACI=33.002%. These values show that a slight change in the original image will result in a significant change in the ciphered image, so the proposed cryptosystem is robust against differential attack [18-22].
Speed analysis
The execution time demonstrates how efficiently the algorithms encrypt/decrypt the images. Table 2 gives the enciphering/deciphering execution time:
| Process Execution Time (sec.) | Figure-1a Lena Image | Figure-1b Satellite View | Figure-1c Medical Image |
|---|---|---|---|
| Encryption | 0.0346 | 0.0378 | 0.1370 |
| Decryption | 0.0345 | 0.0348 | 0.1372 |
Table 2. Enciphering/Deciphering speed test analysis.
Conclusion
The proposed cryptosystem is very fast and it meets the requirements of the normal operations. This scheme employs the linear transformation to scramble the positions of image pixels and uses XOR-plus-mod operation to confuse the relationship between the cipher and the plain images, thereby significantly increasing its resistance to various attacks like differential and statistical attacks. The system is simple, robust and can encrypt/decrypt huge images without losing the image quality and does not suffer from any mathematical complexities. Moreover, the implementation of the algorithm is easy as only integers are used. This system may be useful in the transmission of cipher images in all secret operations, related to medical and defence.
References
- Menezes AJ, Van Oorchot PC, Vanstone SA. Handbook of applied cryptography. CRC Press, Florida, USA 2000.
- Dachselt F, Schwarz W. Chaos and Cryptography. IEEE Trans Circuits System I 2001; 48: 1498-1509.
- Koblitz N. A course in number theory and cryptography, Springer, Berlin 1994.
- Viswanath MK, Ranjithkumar M. A secure cryptosystem using the decimal expansion of an irrational number. Appl Math Sci 2015; 9: 5293-5303.
- Heath-Brown DR. Fermat’s two square theorem. Invariant 1984; 1: 3-5.
- Schneier B. Applied cryptography: Protocols algorithms and Source code in C (2nd Ed). Wiley, New York 1995.
- Mao YB, Chen G, Lian SG. A novel fast image encryption scheme based on the 3D chaotic baer map. Int J Bifurcat Chaos 2004; 14: 3613-3624.
- Chen G, Mao Y, Chui CK. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solit Fract 2004; 21: 749-761.
- Penrose R. A generalized inverse for matrices. Proc Cambridge Philos Soc 1955; 51: 406-413.
- Stanimirovic P; Stankovic M. Determinats of rectangular matrices and Moore-Penrose inverse. Novi sad J Math 1997; 27: 53-69.
- Eisenberg E. Hill ciphers and modular linear algebra. Mimeographed notes, University of Massachusetts, USA 1998.
- Hill LS. Cryptography in an algebraic alphabet. Am Math Month 1929; 36: 306-312.
- Kwok HS, Tang WK. A fast image encryption system based on chaotic maps with finite precision representation. Chaos Solit Fract 2007; 32: 1518-1529.
- Fu C, Huang JB, Wang NN, Hou QB, Lei WM. A symmetric Chaos based image cipher with an improved Bit-level permutation strategy. Entropy 2014; 16: 770-788.
- Annamalai R, Srikanth J, Prakash M. Integrity and privacy sustenance of shared large scale images in the cloud by ring signature. Int J Comput Appl 2015.
- Kocarev L. Chaos-based cryptography: a brief overview. IEEE Circ Syst Mag 2001; 1: 6-21.
- Fridrich J. Symmetric ciphers based on two-dimensional chaotic maps. Int J Bifurcat Chaos 1998; 8: 1259-1284.
- Shannon CE. Communication theory of secrecy system. Bell Syst Tech J 1949; 28: 656-715.
- Kocarev L, Jakimovski G. Chaos and cryptography: from chaotic maps to encryption algorithms. IEEE Trans Circ Syst-I 2001; 48: 163-169.
- Prakash M, Gowsika U, Sathiyapriya S. An identification of abnormalities in dental with support vector machine using image processing. Emerg Res Comput Informat Commun Appl 2015.
- Rhee MY. Cryptography and secure communications. Computer Communication, McGraw-Hill, USA 1994.
- Balamurugan E. Elliptic curve integrated encryption seceme using analysis vehicular ad hoc network. Int J Innovat Sci Eng Res 2016; 3: 47-50.
