Research Article - Biomedical Research (2017) Volume 28, Issue 3
A steganographic approach for realizing medical data privacy in a distributed environment
Manikandan G*, Bala Krishnan R, Rajesh Kumar N, Sairam N and Raajan NRDepartment of Technology, Sastra University, Tamil Nadu, India
- *Corresponding Author:
- Manikandan G
Department of Information and Communication Technology
Sastra University
Tamil Nadu, India
Accepted date: July 7, 2016
Abstract
Organizations like hospitals accumulate huge volume of records from different data sources which may also contain private information. Data mining extract fresh pattern from such data which is used in various domains for proficient decision making. The quandary with data mining is that it also reveal some private information which pose a threat to individual privacy. Privacy Preserving Data Mining (PPDM) gives convincing data mining outcome without revealing the original data. The original medical data is personalized in such a way that the hidden data remains private even after the mining process. In this paper we have proposed a novel scheme for the distributed environment that allows absolute alteration of original medical data using normalization method in each site for generating sanitized data. Coordinator uses a new steganographic approach using contours to send the range to which the data is to be mapped to the desired data owners. The proposed scheme is evaluated in two different dimensions namely privacy and security. Misclassification error is used as a measure to evaluate privacy. For security the experimental results are compared with other steganographic techniques, which show the proposed embedding approach enhances the PSNR of the stego image. This model gives realistic data mining results for analysis purpose without revealing the actual data.
Keywords
Privacy, Security, Normalization, Clustering, Misclassification error.
Introduction
Data mining applications make use of huge quantity of exhaustive individual data that are recurrently collected for analysis. Such data consist of medical history, regular shopping habits and credit records of individuals. On one hand, such data is a significant asset to industry for effective decision making processes and to various government agencies for identifying probable beneficiaries. If not done properly, the investigation of such statistics opens new threats to seclusion and sovereignty of the individual. The threat to privacy becomes authentic as data mining techniques are competent to gain exceedingly insightful facts from uncategorized data that is not even recognized by data owners [1-4]. Preserving privacy has become a key area of research in data mining. There are a number of data distortion or perturbation methods in this category, which will be of our interest in this manuscript [5,6].
Cryptography [7-10] and steganography [11-15] are conceived as the most salient techniques in the security arena to shield the secret information throughout communication. In cryptography, the data is shinned into an indecipherable format before transmission to hide the original contents of the message from an intruder. Steganography hides the secret message without any modification in a medium with the intention that the hidden message is imperceptible for the attackers [16]. A diverse set of mediums namely audio, video and image can be used for this purpose. Image is regarded as the most suitable one among the various cover medium owing to the reality that it achieves realistic hiding capacity [16]. In contrast with cryptography, steganography provides a privileged level of security and privacy as it fabricates the confidential information to be invisible.
In this research work we put forward an innovative method to achieve data privacy in a distributed environment while performing data mining. When there is an appeal for the data, the data owners alter the original data by using a normalization process. The coordinator embedded the range to which the data is to be mapped in an image and transmit the image to the potential data owners. For measuring privacy we employ kmeans clustering scheme to validate the investigational outcomes. On the other hand we compare the PSNR of the proposed scheme with the existing approaches as a measure to express security.
The rest of the paper is organized as follows. Section 2 provides an overview of literature works carried out in privacy preserving techniques and Steganography; section 3 comprises of proposed system. Experimental results are tabulated and compared in Section 4 and finally in Section 5, we arrive to an overall conclusion from our work.
Literature Survey
In [17] Li et al. proposed kd-tree based perturbation method using a recursive divide-and conquer technique. In this method data set is recursively partitioned into smaller subsets, in such a way that the data in each subset are relatively homogeneous. Then the subset average is used to perturb the confidential data in each subset.
In [18] a new approach for data perturbation using Fast Fourier Transform (FFT) is proposed. Wavelet transformation based data distortion to preserve the privacy of data is proposed in [19]. It is proved that this strategy based on wavelet perturbation safeguards the basic statistical properties of original data and it also take full advantage of the data utility. The original dataset is vertically partitioned into several subsets [20]. The owner of the subset can arbitrarily choose a rotation matrix for perturbing their individual data. The results obtained by conducting experiments shows that this scheme for data perturbation conserves the data privacy without disturbing the accuracy.
Peng et al. use a coalesce of data distortion strategies for privacy preservation [21]. The basic inspiration of the proposed approach was to carry out distortion on sub matrices of original dataset using diverse methods. For distortion of sub matrix they make use of different schemes such as Discrete Wavelet Transformation (DWT), Single Value Decomposition (SVD) and Non-Negative Matrix Factorization (NMF). In comparison to the individual data distortion practices the proposed method was very proficient in maintaining data utility as well as data privacy.
The cipher text is embedded in a cover image to generate the desired stego image. Multiresolution wavelet technique is used to reduce the size of the stego image. The uniqueness of this approach is that it conserves the bandwidth [22]. In [23] Shearing based geometrical transformation is used to transform original data. Data utility is achieved using this approach. The Limitation of this approach is that the modified data entirely depends on the noise used. Fuzzy logic can be used to realize privacy. To obtain the modified data a suitable membership function is used. In [24] an s-shaped membership function is used to convert the original data. Data utility depends on the type of membership function used and this method is not suitable for many applications. A proficient approach for data modification utilizing the various operations in geometrical transformations like Translation, scaling along with shearing is proposed [25]. Experiment results demonstrate the usefulness of the modified data in achieving privacy.
Proposed System
A min-max based normalization approach was suggested in this work to preserve data privacy in a distributed environment. The data is presumed to be available with different data owners in diverse locations. The coordinator identifies the prospective data owners when a request for the data is received from the user. The range to which the data is to be mapped is embedded in an image and the stego image is sent to the data owners. The range retrieved from the stego is used for data normalization and the resultant normalized data is transmitted to the coordinator who in turn sends the data to the desired users.
Min-max normalization
Min-Max normalization procedure performs a linear transformation on the original data. The rule employed for changing a value v of an attribute A from range [minA, maxA] to a new range [new_minA, new_maxA] is given by Equation 1.
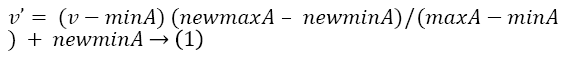
Where v’ is the new value in the given range. The benefit of Min-Max normalization is that it preserves the relationships between the original data values.
Geodesic active contours
Vicent et al. proposed an efficient method for object boundaries detection which uses a technique based on active contours evolving in time according to intrinsic geometric measures of the image. The following mathematical calculation is standardised for object boundaries detection [26].
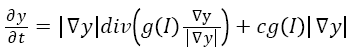 →(2)
→(2)
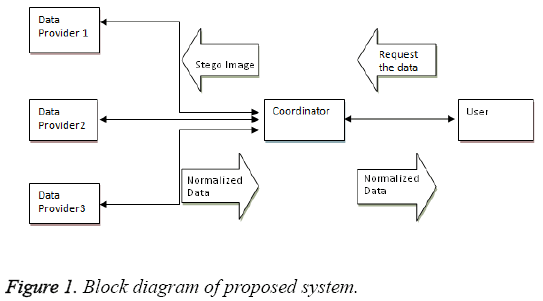
The block diagram of the projected system is shown in Figure 1. The proposed system consists of the following steps:
Step 1: The user sends a request for data to the coordinator.
Step 2: Coordinator identifies the possible data owners.
Step 3: The mapping range is determined by the coordinator.
Step 4: Coordinator selects an image for the embedding process.
Step 5: Coordinator determines the location and size of the contour.
Step 6: To map the contour to a different location a secret key value is used by the coordinator.
Step 7: The range to which the data is to be mapped is embedded in this location using LSB substitution technique which results in a stego image.
Step 8: Stego image is transmitted to the data owners.
Step 9: Data owners extracts the message from the stego image.
Step 10: Normalized data is generated by data owners.
Step11: The normalized result is transmitted to the coordinator.
Step12: Coordinator forwards the normalized data to the requestors.
Simulation and Results
The dataset used in this work is a Bank Marketing Data Set which is related with direct marketing campaigns (phone calls) of a Portuguese banking institution available on UCI Machine Learning Repository [27]. The result obtained by performing normalization on age attribute of the bank marketing data set is shown in Table 1. For experimental purpose we have taken 10 values from the data set and are shown in row 1 and its corresponding normalized value mapped to a range between 10 and 90 is shown in row 2.
| Original data | 2 | 6 | 10 | 14 | 18 | 22 | 26 | 30 | 35 | 40 |
| Normalized data | 10 | 12 | 17 | 26 | 38 | 54 | 68 | 79 | 87 | 90 |
Table 1: Comparison table.
To express the efficiency of our approach we compute misclassification error between the clusters that are obtained after applying K-means algorithm to the original and the modified data. The formula used for computing misclassification error is shown in the Equation 3. The misclassification error is computed by varying the number of instances and the result is tabulated in Table 2.
| Number of Instances | k=2 | k=3 | k=4 |
|---|---|---|---|
| 25 instances | 0.4 | 0.16 | 0.12 |
| 50 instances | 0.6 | 0.4 | 0.96 |
| 75 instances | 0.14 | 0.58 | 0.71 |
Table 2: Misclassification Error for different ‘k’ values.
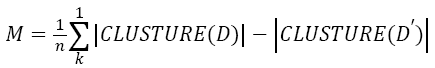 →(3)
→(3)
Where
M is the misclassification error
D represents original data/cluster
D' represents sanitised data/cluster
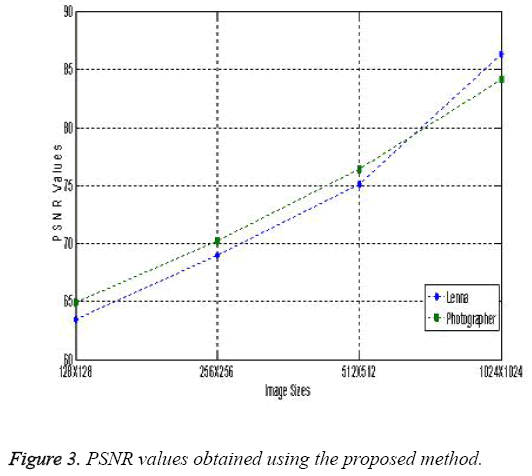
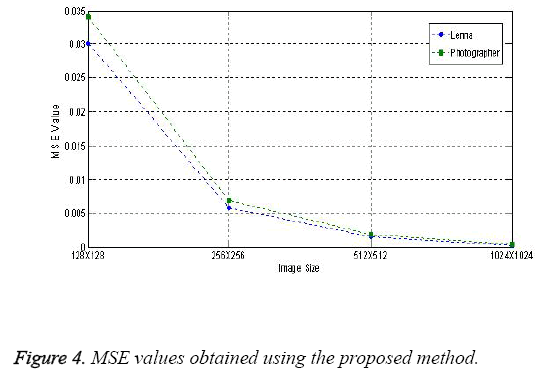
To explain the efficiency of our system we have charted the MSE and PSNR values for different sizes of the image and contour sizes. Table 3 shows the PSNR and MSE values obtained with different standard images namely Lenna and Cameraman. Contours generated by varying the image sizes are shown in Figure 2.
| Input image | 128 × 128 | 256 × 256 | 512 × 512 | 1024 × 1024 | ||||
|---|---|---|---|---|---|---|---|---|
| MSE | PSNR | MSE | PSNR | MSE | PSNR | MSE | PSNR | |
| Lenna | 0.0301 | 63.44 | 0.0058 | 69.01 | 0.0015 | 75.12 | 0.00025 | 86.34 |
| Photographer | 0.034 | 64.89 | 0.0069 | 70.21 | 0.0018 | 76.41 | 0.00042 | 84.12 |
Table 3: Variations observed in stego image and input image for different image sizes.
As noticed from the Table 3, the MSE values are small, representing that the implanting has brought in only extremely miniature errors. The high PSNR appraises that the stego images got after embedding have high accuracy as the original image. The results obtained from the proposed methodology are at the same level with the results obtained from other LSB substitution techniques. The PSNR and MSE values obtained with different image sizes for different images like Lenna and Photographer using the proposed method is shown in Figures 3 and 4.
Conclusion
In this paper we have introduced a new mechanism to maintain data privacy in a distributed environment. The concept normalization is used to generate the sanitized data. The advantage of our approach is that it makes the transformed data seems to be the same as the original data to the end users. The uniqueness in this work is the integration of steganography for achieving privacy in distributed data mining. From our experimental works it is witnessed that the image quality and secrecy are not lost. The strength of our approach lies in contour location, size of contour and the key value. In future our research work can be extended to colour images along with clustering the pixels within the contour which increases the complexity to extract the data for the intruders.
References
- Jiawei H, Micheline K. Data mining-concepts and techniques, Morgan KauffmanPubl 2006.
- Gupta GK.Introduction to data mining with case studies. Prentice hallIndia 2008.
- Margaret HD. Data Mining-Introductory and advanced topics. Pearson Education 2003.
- Soman KP, Shyam D, Ajay V. Insight into data mining-theory and practice. Prentice Hall India 2006.
- Benjamin CMF, KeW,Ada WCF,Philip SY. Introduction to privacy-preserving data publishing: concepts and techniques. Chapman Hall 2010.
- Jaideep V, Christopher W, Clifton, Michael Z.Privacy preserving data mining. Springer (1st edn.) 2005.
- Schneier B.Applied cryptography protocols, algorithm and source code in C.Wiley India (2nd edn.) 2007.
- Denning DER.Cryptography and data security. Addison Wesley Longman 1982.
- Stallings W.Cryptography and network security- principles and practice. Prentice Hall Press 5th (edn.) 2010.
- Ferguson N, Schneier B.Practical cryptography. John Wiley and Sons (1st edn.) 2003.
- Provos N, Honeyman P.Hide and seek-an introduction to steganography.I Secur Privacy 2003; 1: 32-44.
- Katzenbeisser SC. Principles of steganography, in information hiding techniques for steganography and digital watermarking. Artech House 2000; 43-78.
- Bender W, Gruhl D, Morimoto N, Lu A. Techniques for data hiding.Ibm Sys J 1996; 35: 313-335.
- KatzenbeisserS, Petitcolas FA.Information hiding techniques for steganography and digital watermarking. Artech House 2000.
- Fridrich J.Steganography in digital media-Principles, algorithms and applications, CambrUni 2009.
- Cheddad A, Condell J, Curran K, Kevitt P. Digitalimage steganography-survey and analysis of current methods. Sig Proc 2010; 90: 727-752.
- Xiao-Bai L, Sumit S.A tree-based data perturbation approach for privacy-preserving data mining. I Trans Know Data Eng 2006; 18: 1278-1283.
- Shuting X, Shuhua L. Fast fourier transform based data perturbation method for privacy protection. Proc I IntConf Intel SecurInfor 2007; 221-224.
- Lian L, Jie W, Jun Z. Wavelet-Based data perturbation for simultaneous privacy-preserving and statistics-preserving.Proc IIntConf D Min 2008; 27-35.
- Zhenmin L, Jie W, Lian L, Jun Z. Generalized random rotation perturbation for vertically partitioned data sets. Proc I SympComp Intel D Min 2009; 159-162.
- Bo P, Xingyu G, Jun Z. Combined data distortion strategies for privacy-preserving data mining. Proc I IntConfAdvCompTheoryEng 2010; 1-572
- Manikandan G,SairamN, Kamarasan M. A New Approach for Secure Data Transfer based on Wavelet Transform. Int J Net Secur 2013; 15: 88-94.
- Manikandan G,Sudhan R, Vaishnavi.Privacy preserving clustering by shearing based data transformation . ProcIntConf CompContEng2012.
- Karthikeyan B,Manikandan G, Vaithiyanathan V.A fuzzy based approach for privacy preserving clustering. J TheorapplinfoTechnol 2011; 32: 118-122.
- Manikandan G, Sairam N, Sudhan R,Vaishnavi. Shearing Based Data Transformation Approach for Privacy Preserving Clustering. IntConf Comp ComNet Technol2012
- Caselles V, Kimmel R, Sapiro G.Geodesic active contours. Int J Comp Vis 1997; 22: 61-79.
- UCI Data Repository.