Research Article - Journal of Psychology and Cognition (2016) Volume 1, Issue 1
The psychometric properties of confidence: structure across cultures in working adult samples.
Heather E Douglas1*, Dennis Rose2, Lynne McCormack2
1Murdoch University, School of Psychology and Exercise Science, Singapore.
2University of Newcastle, School of Psychology Australia.
- *Corresponding Author:
- Heather Douglas
School of Psychology and Exercise Science
Murdoch University, Singapore Campus
#06-04 Kings Centre, 390 Havelock Road 169662
Singapore.
Tel: +65 6838 0773
E-mail: H.douglas@murdoch.edu.au
Accepted date: October 22, 2016
DOI: 10.35841/psychology-cognition.1.1.81-90
Visit for more related articles at Journal of Psychology and CognitionAbstract
Confidence reflects a belief or faith in oneself, and is measured by embedding ratings within ability tests. The research declaring cross-cultural invariance has examined Confidence using exploratory factor analysis. This is limited to exploring the overall structure or configural invariance, of Confidence. The aim of this study was to examine the measurement invariance of Confidence across two cultural samples, using multi-group confirmatory factor analysis (MGCFA) to extend our knowledge of its structure to metric (item loadings) and scalar (item intercept) properties. In contrast to previous research on school-age children, participants were 1522 adults from Australia (N=833) and Thailand (N=689) who completed the ebilities MAS-2 cognitive ability tests online. Separate confirmatory factor analyses in the cultural samples indicated an acceptable fit of a model with one latent factor representing Confidence. Results of MGCFA supported the configural, metric, and scalar invariance of Confidence across cultures. Evidence for the invariance of a one-factor structure was found across the two national samples. Implications and future research directions in the domain of selection and assessment are discussed.
Keywords
Cross-cultural psychology, Decision making, Intelligence/abilities, Confidence.
Introduction
Introduction Confidence has been receiving increasing attention in individual differences research [1]. Confidence is defined as a form of metacognition or self-monitoring that reflects a person’s perception of their accuracy on a given task. Individuals are asked to answer a test item, following which they are asked to make a judgement about the accuracy of their answer [2,3]. Individuals high in Confidence can be described as decisive, whereas those who are low on it are hesitant about their decision-making capacity [4]. It has been suggested that accurate self-monitoring such as that represented by Confidence is the foundation required to employ more complex metacognitive processes, for example planning and selecting learning strategies [5,6]. Confidence appears to have real-world implications for decision making in workplace contexts [7,8], however, much of the research on its psychometric properties has accumulated in educational settings.
Without a measure validated for use in high stakes cognitive testing, the implications of Confidence for decision-making in employment contexts is poorly understood. Therefore, the primary focus of this study is on the psychometric properties of the ebilities Mental Agility Series 2 (MAS-2), a cognitive ability and Confidence test typically administered in high stakes testing situations. We particularly focused on the consistency of its item-level factor structure across two national samples (Australia and Thailand). Our aim is to demonstrate that, like the measures employed in educational contexts, Confidence can be measured reliably in working adult samples and that it is a unitary psychological trait. In contrast to previous research, at the group level, we sought to examine the invariance of the Confidence factor structure across the two national samples using a more stringent test than has previously been applied to other measures of Confidence.
Theoretical Accounts of Confidence
Studies of Confidence and its realism are typically viewed as elements of metacognition and self-regulated learning, or whether those who know more also know more about how much they know [9]. Accuracy is defined to denote a person’s performance on items from typical cognitive tests, and corresponding confidence on these items is measured by asking participants to state, on a percentage scale, how confident they are that their answer to a just provided test item was correct. Miscalibration or selfmonitoring refers to the ability to appraise the accuracy of one’s cognitive work while doing it [10] and is measured as the discrepancy between the accuracy of the test item and the corresponding Confidence of the individual answering it. Miscalibration can exist as both under confidence (confidence is lower than percentage accuracy on a cognitive test) and over-confidence (confidence is higher than percentage accuracy).
Two theoretical accounts of Confidence in decision-making dominate the literature: the ecological approach [11] and the heuristics and biases approach [12]. The ecological approach to Confidence asserts that the discrepancy between accuracy on test items and Confidence on the same item can be explained in terms of the difficulty of test items. A given person might not know the correct answer to a difficult test item and therefore uses the available and potentially misleading cues to answer the question. For advocates of the ecological approach, the sources of miscalibration reside outside the individual [13]. In contrast, the heuristics and biases approach attributes miscalibration to sources within the individual [4,12]. This second approach is linked to the error model proposed by Soll, which states that miscalibration is due to participants’ limited experience with cognitive test stimuli, and their inconsistency in forming subjective feelings of confidence [14]. This error interacts with the stimulus being presented and may lead to overconfidence [4].
Dougherty proposed an integration of the ecological and error models of Confidence. Dougherty’s model predicts that miscalibration (over-confidence or under-confidence bias) should decrease both as a function of experience with cognitive test items, and as a function of intelligence [15]. This suggests that Confidence consists of a random part including lack of experience with cognitive test items and uncertainty that difficult items on the test introduce [14] and non-random, systematic and reliable individual differences in Confidence. According to Dougherty’s account, Confidence is likely to be positively associated with intelligence. Further, although Confidence ratings are likely to contain random variance associated with item difficulty, the individual differences component in Confidence is likely to be most important for subsequent decision-making. Our focus in this article is on the individual differences approach to Confidence.
Correlates of Trait Confidence
Confidence is an important predictor of accuracy on a test, with correlations in the literature reported between 0.40 and 0.60 [16]. Confidence also predicts achievement on standardized tests within schooling systems [17-19]. For example, Morony et al. investigated the relationship between Confidence and mathematics accuracy in over 7000 secondary school students across Europe and Asia and found that Confidence was the single most important predictor of mathematics accuracy on the Program for International Assessment (PISA) items [18]. Stankov et al. similarly found that Confidence was an excellent predictor of accuracy on both Mathematics (R2=0.484) and English tests (R2=0.362) among a group of 1940 Singaporean secondary school students [19].
Confidence might also prove useful in predicting maladaptive personality styles which have been shown to impact on job performance and individual job satisfaction. One such study by Want and Kleitman investigated the link between imposter feelings and low Confidence in ability, based on the hypothesis that a gap between assessments of one’s ability and task-related achievements (i.e., poor self-monitoring) is at the heart of Imposter Phenomenon (IP) [8]. Supporting the predictions of this study, higher impostor scores correlated with lower Confidence levels, but not with the accuracy score of the test. This validated the original formulation of IP, being high achievers who make unreasonably low assessments of their performance.
Furthermore, as suggested by Want and Kleitman, evidence is emerging for the role of Confidence in effective decision-making [8]. In a study of 196 psychology students exposed to a medical decision-making paradigm under conditions of uncertainty, Jackson and Kleitman found that an increase in Confidence resulted in an incremental increase in congruent, optimal and incompetent decision tendencies (R2=19%, 10% and 9%, respectively), and a decrease in hesitant tendencies (R2=17%) after diagnostic accuracy and intelligence had been accounted for [7]. Using the clinician example given in the study, this indicates that Confidence increases the likelihood that a clinician will correctly diagnose and appropriately treat their patients (optimal), but also that clinicians will treat a patient regardless of diagnosis accuracy (congruent and incompetent). A decrease in Confidence predicts the clinician who tends to request further diagnostic tests despite arriving at a correct diagnosis for a patient (hesitant). Such findings suggest that Confidence has realworld implications that are worthy of investigation in a workplace context.
Structure of Confidence Measures
Confidence appears as a separate, domain-general factor [20]. Results of multiple factor analyses indicate that Confidence forms a single component separate from both accuracy and non-cognitive constructs (such as self-efficacy, self-concept and self-esteem), regardless of the cognitive subtests in which Confidence ratings are provided [4]. A similar structure of Confidence has furthermore been demonstrated across multiple cultural samples. Morony et al. investigated the cross-cultural variance of self-beliefs in adolescent samples in relation to achievement in mathematics in Asia (Singapore, South Korea, Hong Kong and Taiwan) and Europe (Denmark, The Netherlands, Finland, Serbia and Latvia) [18]. Despite the Asian countries being lower on self-concept and higher on mathematics anxiety than European countries, Confidence showed little difference in structure between regions and accounted for most of the variance explained by the other self-constructs combined. These findings suggest that Confidence is unlikely to disadvantage particular cultural groups of job candidates if used in a selection and assessment context.
Limitations of Previous Confidence Research
Despite the evidence that Confidence might have implications for behaviour at work, the research addressing the psychometric properties, structure and utility of Confidence has accumulated primarily in educational settings. Therefore, there is a need to replicate this research in adult working population samples across cultures. As suggested above, much of the research on Confidence has demonstrated that it forms a unitary construct. Much of this research has examined the structure of Confidence using exploratory factor analysis techniques, and has only examined the overall structure of the latent Confidence construct [4,19,21-23]. No research that we are aware of has examined the measurement invariance of Confidence across cultures.
Measurement invariance (MI) is a statistical property of measurement that enables researchers to evaluate whether the same construct is being measured across specified groups [24]. Multiple group confirmatory factor analysis [25] can be used to test for measurement invariance. The MGCFA technique involves applying cross-group constraints on the models and comparing these models with the previous, less restricted model [26]. According to this approach, there are three levels of measurement invariance relevant to comparing scores across cultures [27]: (a) configural invariance (all groups have the same factor structure), (b) metric invariance (the factor loadings of the indicators are equal across the compared groups), and (c) scalar invariance (in addition, all indicator intercepts are equal across groups). Previous research on Confidence has been limited to identifying its configural invariance. Metric invariance is required to compare factor covariances or unstandardized regression coefficients across groups; its presence indicates that a construct has the same metric and the same meaning across groups. Scalar invariance is required to compare construct means across groups; its presence indicates that the scales can be interpreted in a similar way in each group [26,28]. Establishing evidence for both the metric and scalar invariance of Confidence suggests that we can compare individual’s scores on Confidence directly, regardless of their cultural origin. Measurement invariance techniques will be used in the current study to investigate the crossnational differences in the psychometric properties of Confidence in more detail.
Research Aim
The aim of this research was to investigate the measurement invariance properties of the ebilities MAS-2 measure of Confidence within a cognitive ability test typically administered in high stakes testing situations. In contrast to previous research that has only explored the configural invariance or overall structure of confidence, we sought to identify whether Confidence was invariant on its item loadings and intercepts as well. These correspond to metric and scalar invariance respectively. In contrast to previous research exploring the structure of Confidence in school-age participants, we recruited working adults from two separate sources within Australia and Thailand. We expected, in line with previous research conducted by Stankov et al. that a one-component structure of Confidence will replicate across two cultural samples (configural invariance). We also explored whether the indicators (items) of Confidence were all related to the latent variable to the same degree in each cultural sample (metric invariance), and whether the intercepts of these items were similar across groups (scalar invariance).
Methods
Participants
Participants were 1522 adults from Australia and Thailand. The Australian sample consisted of 367 job applicants applying for positions as security guards and 270 adults applying for other white collar and managerial positions who completed the Mental Agility Series 2 (MAS-2) under supervised conditions. The remaining 196 participants completed the MAS-2 in their own time. Many Australian participants were Caucasian (65.9%). The Thailand sample consisted of applicants to graduate positions at a major multi-national corporation. All the participants from Thailand completed the MAS-2 in their own time. Most Thailand participants (98.1%) reported their ethnicity as Asian. Proficiency in the English language is a condition of employment in Thailand; hence the MAS-2 was administered in English to these participants. Sample information for each country is presented in Table 1. Compared to the participants from Thailand, the majority of the Australian sample were male and spoke English as their first language. There were a higher proportion of degree-educated participants in the Thailand sample.
Measures
The ebilities MAS-2 battery was designed to provide two core tests of cognitive abilities: Swaps and Numerical Operations. These tests measure some of the key cognitive abilities described by the theory of fluid and crystallised intelligence [29]. All items included within the battery had cut-off times.
Test of fluid ability (Gf) – Swaps: This was a test of fluid ability that involved working memory. Test-takers were shown a set of three pictures and were given an instruction about swapping the order of the pictures, for example, “Swap 2 and 3”. They were then shown an answer screen, which included the same three pictures in various orders. Participants were asked to select the option that presented the correct sequence of pictures after the swap had been made. A total of 20 test items ranged between 1 and 4 swaps, with item complexity increasing as more swaps were required. The technical manual for this test reports an internal reliability of α=0.97 [29].
| Country | N | Age (SD) | % Female | % English | % Degree |
|---|---|---|---|---|---|
| Australia | 833 | 36.12 (14.85) | 32.2 | 77.3 | 63.6 |
| Thailand | 689 | 24.31 (4.12) | 69.7 | 3.8 | 85.7 |
Table 1. Descriptive statistics of each sample.
Test of quantitative knowledge (Gq) - Numerical operations: This test consisted of mathematical questions that requested the participants to solve by using addition, subtraction, division and multiplication, and select the correct solution to the problem from the four possible options below it. Test-takers were instructed to select the solution to the problem from the options. There were 25 items in the test that varied in difficulty, and were completed without the use of a calculator. The internal reliability of this test was α=0.95.
Confidence: Confidence was measured by embedding survey questions into each of the ability tests. After each test item, participants were asked to rate how confident they were that they answered the preceding question correctly. The response options ranged between 25% confidence (consistent with the chance of guessing the correct answer) and 100% confidence. For each subtest (Swaps and Numerical Operations) an average Confidence score was calculated. The internal reliability on both Swaps and Numerical Operations Confidence indices in the current sample was α=0.95.
Statistical Analyses
Multiple-group confirmatory factor analysis (MGCFA) tests a series of increasingly restrictive models to determine whether the fit is similar across groups. The analyses were performed in AMOS 22.0 [30]. We used three fit indices across all levels of our MGCFA to evaluate model fit. The first was the Normed chi-square (χ2/df), with values between 1.0 and 5.0 indicating acceptable fit in applied settings. The Comparative Fit Index (CFI) compares the fit of a researcher’s model with a more restricted baseline model. Values greater than 0.90 indicate an acceptable model fit [31]. The Root Mean-square Error of Approximation (RMSEA) reflects the degree to which a researcher’s model reasonably fits the population covariance matrix, while taking into account the degrees of freedom and sample size [32]. It is a parsimony-adjusted index that favours simpler models. When the RMSEA value is below 0.05, the model has a very good model fit [33]. When the RMSEA value is 0.08 or less, the model has a reasonable fit [31,34]. Examining these fit statistics gave an indication of the reliability and validity of the model in each national sample.
The analyses consisted of four steps, in which the structure of Confidence was examined using increasingly restrictive models:
1. For both Swaps and Numerical Operations, a Confirmatory Factor Analysis (CFA) was conducted to specify the model of Confidence that would be tested for measurement invariance.
We calculated the one-component Confidence model across our total sample (N=1522) to identify appropriate covariances between items. We conducted this step first to ensure that the covariances tested in the subsequent MGCFAs were consistent across national samples. Consistent with the error model of Confidence [14], the uncertainty that difficult or unfamiliar test items produce are random sources of variance not attributable to the trait Confidence we are attempting to examine. On this basis we added covariances between items similar in content and difficulty. Examination of the standardised residual covariance matrix and the modification indices were used to identify covariance between items that might be due to these sources of variance external to the individual.
2. Before testing measurement invariance, a CFA was performed in both the Australian and Thailand datasets independently to ensure that the measurement model was an acceptable fit in both samples, using maximum likelihood estimation.
3. To assess configural invariance, we ran the MGCFA without any constraints. In subsequent MGCFAs, we added the restrictions needed to test each more stringent level of measurement invariance. Item factor loadings were restricted first as a test of metric invariance. If the fit of the metric invariance model was sufficient, we then tested scalar invariance by restricting item intercepts to be equal across groups.
We used the cut-off criteria suggested by Chen to determine whether the more restrictive models had significantly deteriorated in fit [35]. The criteria for identifying poor metric invariance compared to the configural model in a sample larger than 300, were a change larger than 0.01 in CFI, supplemented by a change larger than 0.015 in RMSEA. The criteria for identifying limited scalar invariance compared with the metric invariance model were a change larger than 0.01 in CFI, supplemented by a change larger than 0.015 in RMSEA. We used changes in CFI larger than 0.01 and changes in RMSEA larger than 0.015 as indicating the absence of invariance [36].
4. We used AMOS 22.0 to identify misspecifications of the model parameters.
For metric invariance, we determined which item loadings caused the largest misspecification. For scalar invariance, we determined which item intercept caused the largest misspecification. We then released only the misspecified items and repeated the analysis. After detecting the largest misspecification and releasing non-invariant parameters, we relied on the global fit measures of the final models to evaluate model fit in the manner described above.
Procedure
Participants completed the MAS-2 online using a unique username and password to log in to the ebilities testing platform. The tests were always administered in the following order: Swaps and Numerical Operations. All items had a cut-off time for completion. Six hundred and thirty-seven Australian job applicants completed the MAS- 2 under supervised test conditions. The remaining 196 Australian test-takers and the Thailand sample completed the MAS-2 unsupervised in their own time. There were no differences in scores on the MAS-2 on either accuracy or Confidence dependent on the supervised nature of the test. Approval for the study was granted by the university’s Human Research Ethics Committee.
Results
Before conducting our invariance analyses, we examined the correlation between overall Confidence and General Mental Ability (GMA), calculated as a composite of Swaps and Numerical Operations accuracy. Consistent with the previous literature indicating a relationship between ability and Confidence, there was a strong and positive correlation between Confidence and GMA across samples, r=0.59, p<0.001. There was no significant difference in the correlation between Confidence and GMA for the Australian (r=0.53, p<0.001) and Thailand (r=0.51, p<0.001) samples, z=0.48, p=0.32.
Measurement Invariance Tests
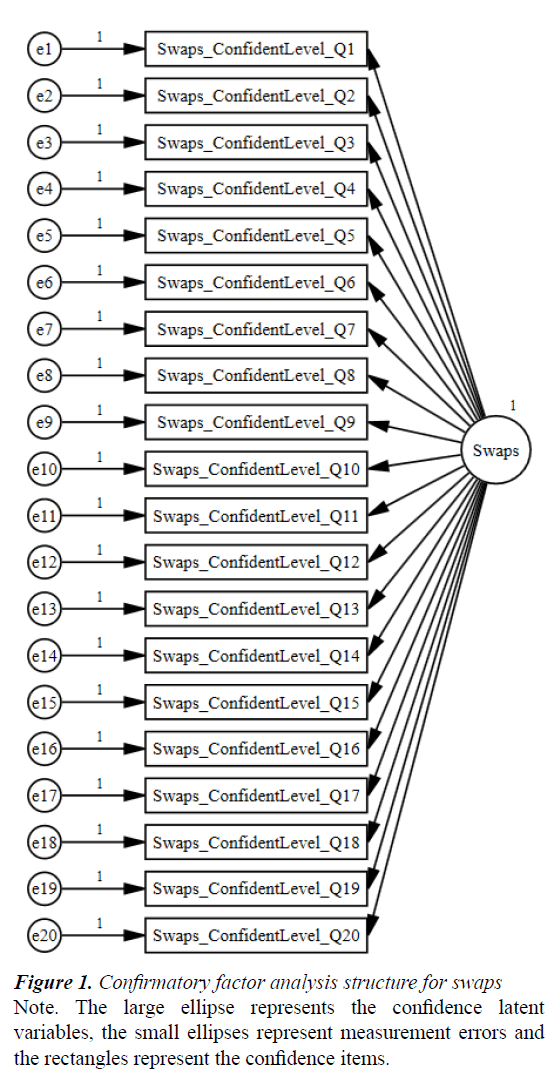
We first tested whether the one-factor model of Confidence fitted the empirical data from each national sample. A one-component model was specified with each item on Confidence serving as an indicator. Figure 1 illustrates the model for Confidence on Swaps. Swaps Confidence demonstrated acceptable fit for the Australian (χ2 (132)=483.045, p<0.001; χ2/df=3.659; CFI=0.969; RMSEA=0.057) and Thailand samples (χ2 (132)=488.532, p<0.001; χ2/df=3.701; CFI=0.957; RMSEA=0.063). Numerical Operations Confidence similarly demonstrated acceptable fit for the Australian (χ2 (247)=927.713, p<0.001; χ2/df=3.755; CFI=0.951; RMSEA=0.058) and Thailand samples (χ2 (247)=641.299, p<0.001; χ2/ df=2.596; CFI=0.948; RMSEA=0.048). Overall these results indicated that the one-factor model of Confidence was strongly supported for both tests in both national samples.
MGCFA was then run. Age and gender were not significant predictors of confidence ratings in either national sample; therefore they were not included as control variables in the models. MAS overall intelligence scores were included to control for the association between Confidence and cognitive ability in all models. Table 2 presents the fit indices for Swaps and Numerical Operations Confidence.
| Model | χ2 (df) | χ2/df | CFI | RMSEA | ΔCFI | ΔRMSEA |
|---|---|---|---|---|---|---|
| Swaps | ||||||
| 1. Configural | 971.613 (264)* | 3.680 | 0.964 | 0.042 | ||
| 2. Metric | 1108.682 (284)* | 3.904 | 0.958 | 0.044 | 0.006 | 0.002 |
| 3. Scalar | 1242.918 (304)* | 4.089 | 0.952 | 0.045 | 0.006 | 0.001 |
| Numerical Operations | ||||||
| 1. Configural | 1568.995 (494)* | 3.176 | 0.950 | 0.038 | ||
| 2. Metric | 1920.245 (519)* | 3.700 | 0.935 | 0.042 | 0.015 | 0.004 |
| 3. Scalar | 2114.625 (544)* | 3.887 | 0.927 | 0.044 | 0.008 | 0.002 |
Notes: *=p<0.001; Δ=change in; Change in CFI and RMSEA are reported as absolute values.
Table 2. Fit indices for invariance tests for accuracy and confidence.
The configural models were an excellent fit to the data in both the Australian and Thailand samples. This indicates that the same structure was an appropriate model for representing the variance in Confidence for Swaps and Numerical Operations, in both national samples.
As configural invariance was supported, we then constrained the factor loadings to be equal across both groups as a test of metric invariance. The fit of the metric models for Swaps and Numerical Operations can be found in Table 2. There was a significant difference in chi-square between the configural and the metric model for Swaps (χ2 (20)=137.069, p<0.001) and Numerical Operations (χ2 (25)=351.25, p<0.001). The change in CFI did not exceed 0.01, nor did the change in RMSEA exceed 0.015 for the Swaps model. Although the change in CFI exceeded 0.01 for the Numerical Operations model, this was not supplemented by a change of more than 0.015 in the RMSEA value. As can be seen in Table 2, the metric model for both tests was an excellent fit to the observed data. The full metric invariance of Confidence was supported across Australian and Thai test-takers.
Because the MGCFA indicated full metric invariance, the item intercepts of all items were then constrained to be equal across groups as a test of scalar invariance. The fit of the scalar models for both Swaps and Numerical Operations are reported in Table 2. A significant difference was observed between the metric and scalar models for Swaps (χ2 (20)=134.236, p<0.001) and Numerical Operations (χ2 (25)=194.38, p<0.001). The difference in CFI and RMSEA between the metric and the scalar models did not exceed the cut-off criteria suggested by Chen [35]. The scalar models for both Swaps and Numerical Operations indicated an excellent fit to the observed data, suggesting that Confidence exhibited scalar invariance properties across both tests in both national samples.
Discussion
The results indicated support for the study hypothesis. As expected, Confidence demonstrated stability in a one-component structure across samples, as evidenced by the excellent fit of the configural models for Swaps and Numerical Operations. In addition, Confidence demonstrated both metric and scalar invariance across cultures. This supported our expectations that Confidence would exhibit the same structural properties regardless of the culture it was administered in, and suggests some implications for the use of the Confidence construct across diverse job seeker populations.
The support for both metric and scalar invariance indicates that the Confidence scale has the same metric value across groups. This means that we can calculate an average score across Confidence test items and compare these scores between any two individuals, regardless of their cultural origin. MGCFA is a much more stringent test of the measurement invariance of the scale and so forms a much more rigorous test of the structural measurement properties of Confidence than has previously been applied in adolescent samples. Measuring within groups and comparing individual scores within these groups is appropriate, as is comparison across the national samples of Australia and Thailand. This suggests that comparing means across groups is likely to be a culture-fair assessment of individual differences in Confidence. Examination of the meaning of Confidence across cultures appears warranted, particularly its implications for subsequent workplace performance.
These findings appear to support a model of Confidence and its assessment that does not depend on the culture it is administered in, consistent with the body of evidence accumulated on Confidence in educational settings. However, in some cases the research indicates that national samples exhibit differences in Confidence. Morony et al. examined the cross-cultural invariance of mathematics self-beliefs in Confucian Asian and European countries, and found significant differences in mathematics Confidence between national samples [18]. This was despite finding limited evidence for differences between European and Asian regions (Cohen’s d=0.12). Acker and Duck investigated cross-cultural overconfidence in the context of behavioural finance models and biased selfattribution, which is the tendency to view one’s superior ability as evidence of skill, while attributing evidence contrary to superior performance as sabotage or bad luck. In a sample of 111 third-year undergraduate finance students participating in the stock-market game, Asians significantly over-predicted their rank relative to other students in the activity compared to British participants. This was despite there being no difference in biased self-attribution found between groups. Acker and Duck suggested that the increased Confidence of Asians was not because they had inflated views of their own abilities [37]. In contrast to these findings, the current analyses appear to suggest that Asian cultures such as the Thailand sample presented here might be responding to the question asking them to rate their certainty of a correct answer in a similar way to predominantly European countries such as Australia. Like Stankov et al., we found evidence for the configural invariance of Confidence. We further extended the evidence of measurement invariance to both the item loadings (metric) and their intercepts (scalar). These findings suggest there is validity in comparing trait Confidence across cultures.
Limitations
Some limitations are present in the current data. The first is the high proportion of males in the Australian dataset. Given that Confidence exhibits some evidence of gender differences [38], the relative lack of females in this sample might have impacted on the plausibility of the structural model presented above. We examined the measurement invariance models within each culture separately for each gender, and found no evidence that gender affected the fit of the model structural estimates, indicating that the gender imbalance in the Australian example is unlikely to have had undue influence on the MGCFA estimates.
Second, data was examined from two geographic regions only, Australia and Thailand. Stankov and Lee examined confidence across nine world regions based on samples from 33 nations and found that differences between nations on cognitive ability were greater than they were on confidence ratings [23]. A similar approach was not taken here because the data on multiple national samples is not yet available on the MAS-2 for working adults. Although we have demonstrated that the measurement properties of Confidence in a sample of adult test-takers are invariant, culture might play a role in how this Confidence is expressed. For example, Australian individuals might express Confidence because of a cultural norm that expects individuals to be certain about their judgements on tests. In contrast, individuals from Thailand might interpret and respond to Confidence questions based on a cultural norm to express Confidence despite having lower self-beliefs. This difference in expression could stem from different interpretations of what is being asked differences in self-promotion, beliefs about the self and Confidence, or cultural pressures on employees to respond in a certain way to questions about Confidence. Because our research was quantitative in nature, we were unable to examine whether there were differences in the expression of Confidence across Australian and Thailand test-taker samples. Further research might wish to examine the determinants of Confidence across cultures in a qualitative manner to identify some of the ways in which Confidence is expressed in Australia compared to Thailand. Future research might also seek to investigate the domaingenerality of Confidence amongst working adults across a broader range of cultural groups.
A further limitation of this dataset is the lack of information on the relationship between Confidence and other variables typically measured in employment contexts, most notably personality. In student populations the construct of Confidence has been linked to personality traits, with consistently small correlations (r=0.30) between Confidence and the openness factor from the Big 5 model being noted by Pallier et al. and Stankov and Lee [4,39]. Among a sample of working adults, low levels of Confidence were associated with a sense of inferiority and self-criticism and the fear of being unable to replicate one’s own success that has come to be associated with the imposter phenomenon [8]. Future research might investigate the association between Confidence and personality in working adult samples, to confirm that Confidence is a factor distinct from both ability and personality, and to investigate the existence of personality correlates of Confidence in working adults.
Implications
Most of the previous research in this area has focused on the psychometric properties of Confidence in adolescent and secondary school samples. In contrast, the current paper explores the structure of Confidence in a group of working adults taking a test for employment selection. There is the possibility that the psychometric properties of the test could be different in a group of working adults undergoing a high-stakes testing situation. We have now established through the current research that this is not the case. This means that the measurement of Confidence is minimally affected by the testing situation or the age of the sample being targeted.
The current research also extends the methodological rigour with which the structure of Confidence was assessed. Most previous research in this area has been conducted using exploratory factor analysis only. As explained in the introduction, exploratory factor analysis is limited to testing the overall structure of measurement instruments. It does not indicate whether the factor loadings of individual items or their intercepts are similar. Both features are needed in addition to a similar structure across cultures, to compare latent means or average scores across groups. MGCFA allowed us to extend the evidence for the measurement invariance of Confidence across cultures, and it suggests that it is valid to compare mean scores on Confidence across cultural boundaries.
Finally, much of the previous research on the psychometric properties of Confidence has been conducted by the same research team, on the same demographic samples [1,3,4,10,16,18,19,21-23,39-43]. Given that the research team across these previous studies has been similar, this introduces the possibility of a bias in this body of research. The current study not only replicates the findings of these authors, it does so with a more rigorous method, and it demonstrates that their findings in adolescents generalize to working adults.
Future Research Directions
Decision-making is a complex process, and a body of evidence exists in support of the central role of general cognitive ability to optimal decision-making. For example, Gonzalez has shown that an individual’s performance on a dynamic decision-making task under high workload is related to cognitive abilities [44]. Other person characteristics like Confidence are also recognized for their contribution to the decision-making process. Parker and Fischhoff put forward the view that making accurate judgements about one’s own competence is critical to effective decision-making [45]. They further contended that people with unwarranted Confidence might neglect signals that they require further information, assistance from others, or that their decisions are faulty. On the other hand, individuals with low Confidence might needlessly hesitate defer to others more often or are doubtful of their ability to make sound decisions. More recently, Jackson and Kleitman concluded that metacognitive Confidence, despite being typically ignored in preference for Intelligence, is an important psychological construct to be included in the study of decision-making processes [7]. A potentially valuable line of investigation in employment settings may look to establish if Confidence demonstrates incremental validity above general mental ability in predicting job performance criteria reflective of optimal decision-making.
The validity of Confidence in decision-making might further extend past working life and into implications for older adults. In a study of driver confidence among community-dwelling older adults, Reindeau et al. identified that Confidence in driving ability was unrelated to on-road driving performance [46]. These findings suggest that older adults might continue to drive based on a faulty degree of confidence in their skill. However, the implications of confidence for older adults might not be unremittingly negative. A recent study of US adults demonstrated that even after controlling for knowledge of investing and saving for retirement, individuals with greater confidence were more likely to report using financial planning services for retirement and were more successful at minimizing fees in a hypothetical investment task [47]. Cognitive ability is further implicated in the medication adherence of older adults with chronic conditions [48,49]. Confidence might influence the association between cognitive ability and medication adherence behaviours in older adults. Future research might wish to explore the role of confidence in health behaviours.
Conclusion
This research sought to establish that confidence can be reliably measured via tests developed for use in selection and development contexts, and that it can be identified as an individual difference factor. In this regard, the study set out to replicate findings on the psychometric properties of the confidence construct as measured within tests administered to adolescents and undergraduate university students. The results of this study demonstrated that the current confidence measure also reflects a domain-general and trait-like construct in a sample of working adults. Consistent with our predictions, a one-component structure of confidence, with invariant item loadings and intercepts was found. This means that the confidence construct is unlikely to vary depending on the country it is administered within. The development of this measure not only has implications for research on confidence in employed adult samples, but might also provide a marker of potentially important workplace behaviours such as decision-making, valuable to selection and assessment professionals. Further investigation is required to determine the exact nature of these relationships, their personality correlates, and their implications for the organisational and national context.
Acknowledgement
Thanks go to Lewis Cadman Consulting for providing the MAS2 data. This research was funded by a University of Newcastle Pilot Linkage Grant G1400303.
Conflict of Interest
The first author received research grants from Lewis Cadman Consulting, the owners of the data reported in this manuscript. The second and third authors have no conflicts of interest.
References
- Stankov L, Lee J. Overconfidence across world regions. Journal of Cross-Cultural Psychology 2014; 45: 821-837.
- Mengelkamp C, Bannert M. Accuracy of confidence judgments: Stability and generality in the learning process and predictive validity for learning outcome. Memory & Cognition 2010; 38: 441-451.
- Stankov L, Kleitman S, Jackson SA. Measures of the trait of confidence. Measures of Personality and Social Psychology, Elsevier Science, Burlington 2015; 158-189.
- Stankov L, Lee J. Confidence and cognitive test performance. Journal of Educational Psychology 2008; 100: 961-976.
- Baker SF, Fogarty GJ. Confidence in cognition and interpersonal perception: Do we know what we think we know about our own cognitive performance and personality traits? 39th Australian Psychological Society Annual Conference: Psychological Science in Action, Melbourne, Australia 2004.
- Was CA. Discrimination in measures of knowledge monitoring accuracy. Advances in Cognitive Psychology 2014; 10: 104-112.
- Jackson SA, Kleitman S. Individual differences in decision-making and confidence: Capturing decision tendencies in a fictitious medical test. Metacognition and Learning 2014; 9: 25-49.
- Want J, Kleitman S. Imposter phenomenon and self-handicapping: Links with parenting styles and self-confidence. Personality and Individual Differences 2006; 40: 961-971.
- Lichtenstein S, Fischoff B. Do those who know more also know more about how much they know? Organizational Behavior and Human Performance 1977; 20: 159-183.
- Kleitman S, Stankov L. Ecological and person-oriented aspects of metacognitive processes in test-taking. Applied Cognitive Psychology 2001; 15: 321-341.
- Gigerenzer G, Hoffrage U, Kleinbolting H. Probabilistic mental models: A Brunswikian theory of confidence. Psychol Rev 1991; 98: 506-528.
- Kahneman D, Slovic P, Tversky A. Judgements under uncertainty: Heuristics and biases. Cambridge, Cambridge University Press, England 1982.
- Juslin P, Olsson H. Thurstonian and Brunswikian origins of uncertainty in judgment: A sampling model of confidence in sensory discrimination. Psychol Rev 1997; 1042: 344-366.
- Soll JB. Determinants of overconfidence and miscalibration: The roles of random error and ecological structure. Organizational Behavior and Human Decision Processes 1996; 652: 117-137.
- Dougherty MR. Integration of the ecological and error models of overconfidence using a multiple-trace memory model. J Exp Psychol Gen 2001; 1304: 579-599.
- Stankov L. Noncognitive predictors of intelligence and academic achievement: An important role of confidence. Personality and Individual Differences 2013; 55: 727-732.
- Fritzsche ES, Kroner S, Dresel M, et al. Confidence scores as measures of metacognitive monitoring in primary students? Limited validity in predicting academic achievement and the mediating role of self-concept. Journal for Educational Research Online 2012; 4: 120-142.
- Morony S, Kleitman S, Lee YP, Stankov L. Predicting achievement: Confidence vs. self-efficacy, anxiety and self-concept in Confucian and European countries. International Journal of Educational Research 2013; 58: 79-96.
- Stankov L, Lee J, Luo W, et al. Confidence: A better predictor of academic achievement than self-efficacy, self-concept and anxiety? Learning and Individual Differences 2012; 22: 747-758.
- Kleitman S, Gibson J. Metacognitive beliefs, self-confidence and primary learning environment of sixth grade students. Learning and Individual Differences 2011; 21: 728-735.
- Stankov L, Crawford JD. Confidence judgements in studies of individual differences. Personality and Individual Differences 1996; 21: 971-986.
- Stankov L, Crawford JD. Self-confidence and performance on tests of cognitive abilities. Intelligence 1997; 25: 93-109.
- Stankov L, Morony S, Lee YP. Confidence: The best non-cognitive predictor of academic achievement? Educational Psychology: An International Journal of Experimental Educational Psychology 2014; 341: 9-28.
- Horn J, McArdle J. A practical and theoretical guide to measurement invariance in aging research. Experimental Aging Research 1992; 18: 117-144.
- Joreskog KG. Statistical analysis of sets of congeneric tests. Psychometrika 1971; 362: 109-133.
- Steenkamp JBEM, Baumgartner H. Assessing measurement invariance in cross-national consumer research. Journal of Consumer Research 1998; 25: 78-90.
- Milfont TL, Fischer R. Testing measurement invariance across groups: Applications in cross-cultural research. International Journal of Psychological Research 2010; 3: 111-121.
- Byrne BM, Shavelson RJ, Muthen B. Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychological Bulletin 1989; 105: 456-466.
- Ebilities. Technical Monograph 2005.
- Arbuckle JL. IBM SPSS Amos 22.0 User's Guide. IBM, Armonk, NY 2013.
- Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling 1999; 6: 1-55.
- Brown TA. Confirmatory factor analysis for applied research. Guilford Press, New York, NY 2006.
- Browne MW, Cudeck R. Alternative ways of assessing model fit. Testing structural equation models, Newbury Park, CA, Sage 1993; 136-162.
- Marsh HW, Hau K-T, Wen Z. In search of golden rules: Comment on hypothesis-testing approaches to setting cut-off values for fit indexes and dangers in overgeneralizing Hu and Bentler's 1999 findings. Structural Equation Modeling 2004; 11: 320-341.
- Chen F. Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling 2007; 14464-14504.
- Byrne BM, Stewart SM. The MACS approach to testing for multigroup invariance of a second-order structure: A walk through the process. Structural Equation Modeling 2006; 13287-13321.
- Acker D, Duck NW. Cross-cultural overconfidence and biased self-attribution. The Journal of Socio-Economics 2008; 37: 1815-1824.
- Pallier G. Gender differences in the self-assessment of accuracy on cognitive tasks. Sex Roles 2003; 48: 265-276.
- Pallier G, Wilkinson R, Danthiir V, et al. The role of individual differences in the accuracy of confidence judgements. The Journal of General Psychology 2002; 129: 257-299.
- Kleitman S, Stankov L. Self-confidence and metacognitive processes. Learning and Individual Differences 2007; 17: 161-173.
- Lee J, Stankov L. Higher-order structure of non-cognitive constructs and prediction of PISA 2003 mathematics achievement. Learning and Individual Differences 2013; 26: 119-130.
- Stankov L. Mining on the "no man's land" between intelligence and personality. Learning and individual differences: Process, trait and content determinants. American Psychological Association, Washington, DC, USA 1999.
- Stankov L. Complexity, metacognition and fluid intelligence. Intelligence 2000; 282: 121-143.
- Gonzalez C. Task workload and cognitive abilities in dynamic decision making. Human Factors 2005; 471: 92-101.
- Parker AM, Fischhoff B. Decision-making competence: External validation through an individual-differences approach. Journal of Behavioral Decision Making 2005; 181: 1-27.
- Reindeau JA, Maxwell H, Patterson L, Weaver B, Bedard M. Self-rated confidence and on-road driving performance among older adults. Canadian Journal of Occupational Therapy 2016; 833: 177-183.
- Parker AM, de Bruin WB, Yoong J, Willis R. Inappropriate confidence and retirement planning: Four studies with a national sample. Journal of Behavioral Decision Making 2012; 244: 382-389.
- Insel K, Morrow D, Brewer B, et al. Executive function, working memory and medication adherence among older adults. Journal of Gerontology 2006; 61B2: 102-107.
- Zogg JB, Woods SP, Sauceda JA, et al. The role of prospective memory in medication adherence: A review of an emerging literature. Journal of Behavioral Medicine 2012; 35: 47-62.