Research Article - Biomedical Research (2018) Artificial Intelligent Techniques for Bio Medical Signal Processing: Edition-II
The analysis and design of a 50MHz Colpitts low phase noise crystal oscillator
Yan Wang*, Ying Cui and Shiyi Xu
School of Electrical Engineering and Information, Southwest Petroleum University, No.8 Xindu Avenue, Xindu District, Chengdu City, Sichuan Province, PR China
- *Corresponding Author:
- Yan Wang
School of Electrical Engineering and Information
Southwest Petroleum University, PR China
Accepted on August 30, 2017
DOI: 10.4066/biomedicalresearch.29-17-505
Visit for more related articles at Biomedical ResearchAbstract
Crystal oscillators have huge demand in medical filed especially in building medical devices. They are used in diagnostic equipment, monitoring devices, hearing aids, etc. Since they are widely used in medical devices, it is essential to maintain accurate requirements for the output phase noise of reference frequency source. At the same time it is important to find out new ways to reduce the phase noise which is the major problem in designing crystal oscillators. The importance of loaded quality factor QL is analyzed on the basis of Leeson model and the formula of QL is derived from the analysis of Colpitts oscillator circuit. According to the results, we can draw a conclusion that QL is explicitly related to circuit parameters. The phase noise of the 50MHz Colpitts crystal oscillator is simulated by the Agilent Advanced Design System (ADS). Based on the simulation results, a design of the prototype crystal oscillator is presented. The crystal resonator we use is AT-cut 3rd overtone crystal resonator with 49 U resistance welding package, its unloaded quality factor Q0 is about 1.45 × 105. The measured results of phase noise are -107 dBc/Hz@10Hz, -134 dBc/Hz@100Hz and -152 dBc/Hz@1KHz. Experimental results show that it is feasible to design low phase noise crystal oscillators on the basis of improving QL.
Keywords
Leeson model, Loaded quality factor, Phase noise, Colpitts crystal oscillator.
Introduction
With the development of modern communication technology, the requirement of the high stable crystal oscillator has increased. Crystal oscillators have numerous applications and they are widely used in medical devices such as defibrillators, neuro-stimulators, hearing aids, pacemakers, etc. [1]. They are also used in ultrasound, MRI equipment, wireless telemetry and diagnostic imaging. Neurologists often use oscillators for treating neurological disorders such as Parkinson’s Disease through deep brain stimulation (DBS) [2,3]. Functional pacemakers coordinating circadian rhythms are constructed by coupling multiple oscillators. Circadian oscillators constitute positive and negative elements which can form autoregulatory feedback loops. These loops are used to generate 24-hour timing circuits [4,5]. Patients with middle ear dysfunction use Bone Anchored Hearing Aids which contains bone oscillators [6]. In many systems such as the medical field, satellite communication and radar system, there are very strict accuracy requirements for the output phase noise of reference frequency source. Therefore, the study of ways to reduce the phase noise is the primary problem in the process of design crystal oscillators [7-9].
In practical design, the phase noise is closely related to QL. By the analysis of Leeson formula derived from the phase noise model of Leeson, we can draw a conclusion that phase noise improves with the loaded quality factor QL increasing. The Leeson formula is as follows [10-13]:
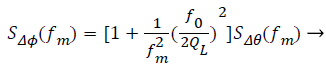 (1)
(1)
Where fm is offset frequency, f0 is center frequency, QL is loaded quality factor, SΔϕ(fm) is the power spectral density of the output phase noise, SΔϕ(fm) is the spectral density of the oscillator input phase noise. So a high QL is beneficial to reducing phase noise.
In this paper, the formula of QL is derived by the analysis of Colpitts oscillator circuit and we can obtain the relation between QL and circuit parameters. An appropriate increase in the value of capacitance C2 can improve QL, thereby reduce the phase noise. According to the simulation results of 50 MHz Colpitts crystal oscillator using Agilent Advanced Design System (ADS), a design of the prototype crystal oscillator is presented and the measurement results of phase noise are reduced by adjusting the value of C2.
The phase noise analysis of colpitts crystal oscillator
From the viewpoint of oscillator power spectrum, for BJT oscillator, the QL factor of a conventional two-port network is defined as [14-16]:
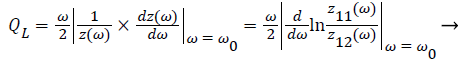 (2)
(2)
Where z11(ω) and z12(ω) are terms of the circuit impedance matrix Z.
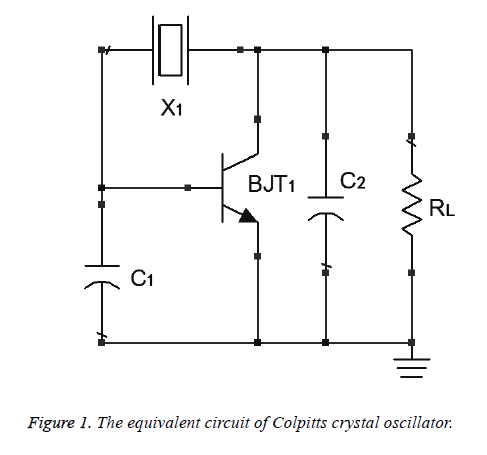
As an example, a modified 50MHz Colpitts low phase noise crystal oscillator is discussed [17]. The equivalent circuit is shown in Figure 1.
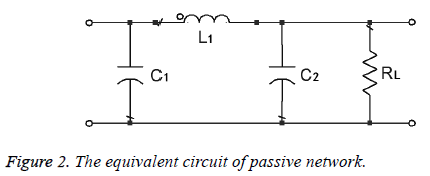
In the above circuit, the crystal resonator X1 acts as an inductance L1. The equivalent circuit of passive network is shown in Figure 2.
The impedance matrix Z of passive network in the circuit is expressed as follows:
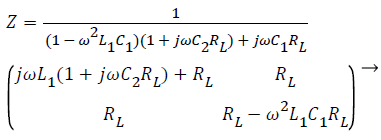 (3)
(3)
According to (2) and (3), the result of QL is as follows:
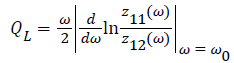
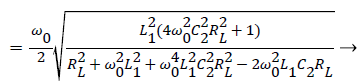 (4)
(4)
From (4), we can draw a conclusion that QL would increase with C2, that is to say, the larger C2, the higher QL.
The simulation and design of colpitts crystal oscillator
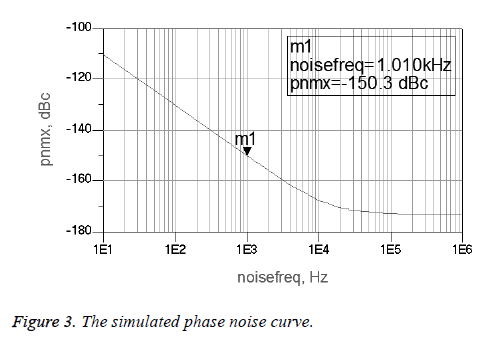
The 50 MHz Colpitts crystal oscillator that its equivalent circuit is shown in Figure 2 is simulated by software ADS and the simulated phase noise curve is shown in Figure 3.
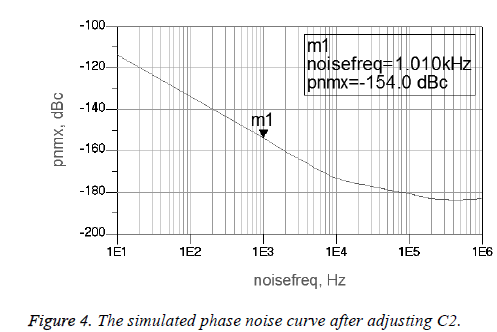
The value of C2 is increased appropriately to improve the value of QL and reduce the phase noise. The simulated phase noise curve after adjusting C2 is also presented in Figure 4.
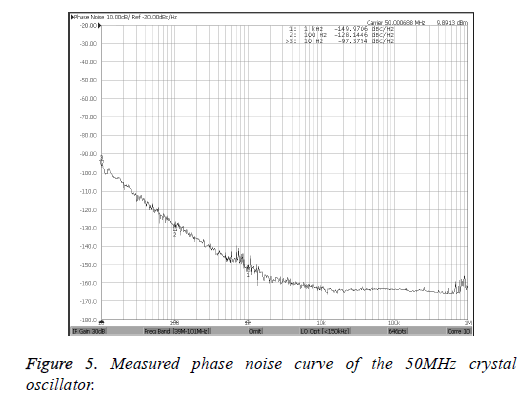
According to the simulation results by ADS, the phase noise is decreased after adjusting C2. Meanwhile, we can draw the conclusion that an appropriate increase in the value of C2 will help to reduce the phase noise of this circuit. However, if C2 is too large, the oscillation condition of the amplitude cannot be met and it is difficult to produce oscillation. Therefore in the allowable range, C2 should be made as high as possible to reduce the phase noise. Based on the conclusions above, a prototype 50 MHz Colpitts crystal oscillator is designed. The AT-cut 3rd overtone crystal resonator with 49 U resistance welding package is used in the design and its quality is medium. Its parameters are as Table 1 and the value of unloaded quality factor Q0 is about 1.45 × 105. The phase noise level of the 50MHz Colpitts crystal oscillator is measured by Agilent E5052B and it is shown in Figure 5.
| Parameter | Value |
|---|---|
| Lq | 0.012 H |
| rq | 26 Ω |
| Cq | 8.4 × 10-16 F |
| C0 | 2.2 × 10-12 F |
Table 1. The parameters of crystal resonator.
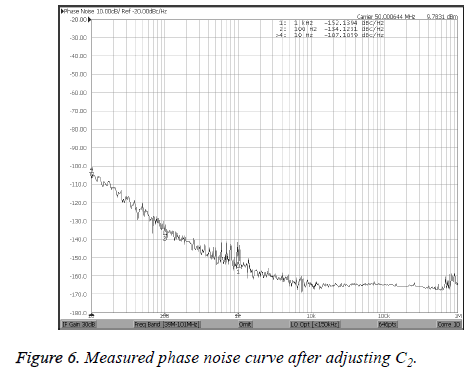
As in Figure 5, the measured results of phase noise are -97 dBc/Hz@10Hz, -128 dBc/Hz@100Hz and -149 dBc/ Hz@1KHz. Based on above analysis, the value of capacitance C2 is adjusted to reduce the phase noise further. The measured results of phase noise level after adjusting C2 are -107 dBc/ Hz@10Hz, -134 dBc/Hz@100Hz and -152 dBc/Hz@1KHz and it is shown in Figure 6.
According to Figure 6, the phase noise is improving by adjusting the value of capacitance C2. Though the crystal resonator used in the design is medium, the measured results of phase noise are relatively well and the crystal resonator’s performance is realized as far as possible by the design based on improving QL.
Conclusion
In this paper, the 50 MHz Colpitts crystal oscillator is designed on the basis of improving QL. Based on the simulation results by ADS, a design of the prototype 50 MHz crystal oscillator is presented and the experiments are carried out. By adjusting the value of capacitance C2, the phase noise level is further improved and the performance of the crystal resonator is realized as far as possible. So it is feasible to design low phase noise crystal oscillators on the basis of improving QL.
Acknowledgement
This work is supported by application fundamental research fund of SiChuan Provincial Science and Technology Department (No. 2014JY0208) and scientific research starting project of SWPU (No. 2014QHZ026).
References
- https://www.elprocus.com/crystal-oscillator-circuit-and-working/
- Wilson D, Moehlis J. Clustered Desynchronization from High-Frequency Deep Brain Stimulation. PLoS Comput Biol 2015; 11: e1004673.
- Holt B, Wilson D, Shinn M, Moehlis J, Netoff TI. Phasic Burst Stimulation: A Closed-Loop Approach to Tuning Deep Brain Stimulation Parameters for Parkinson’s Disease. PLoS Comput Biol 2016; 12: e1005011.
- Evans JA, Elliott JA, Gorman MR. Dynamic interactions between coupled oscillators within the hamster circadian pacemaker. Behavioral Neurosci 2010; 124: 87-96.
- Bell-Pedersen D, Cassone VM, Earnest DJ, Golden SS, Hardin PE, Thomas TL, Zoran MJ. Circadian rhythms from multiple oscillators: lessons from diverse organisms. Nat Rev Genetics 2005; 6: 544-556.
- Chasin M. Bone Conduction Implants: The When and Why. Hearing Rev 2000.
- Apte M, Poddar AK, Rudolph M, Rohde UL. A novel low phase noise X-band oscillator. IEEE Microwave Magazin 2015; 16: 127-135.
- Mazzanti A, Bevilacqua A. On the phase noise performance of transformer-based CMOS differential-pair harmonic oscillators. IEEE Transact Circuits Syst I 2015; 62: 2334-2341.
- Gouhary EL, Neihart NM. An analysis of phase noise in transformer-based dual-tank oscillators. IEEE Transact Circuits Syst I 2014; 61: 2098-2109.
- Leeson B. A simple model of feedback oscillator noises spectrum. Proc IEEE 1966; 54: 329-330.
- Sauvage G. Phase noise in oscillator: a mathematical analysis of Leeson model. IEEE Transact Instrument Measurement 1977; 26: 408-410.
- Galliou S, Sthal F, Mourey M. New phase noise model for crystal oscillators application to the Clapp oscillator. IEEE Transact Ultrasonics, Ferroelectrics, Frequency Control 2003; 50: 1422-1428.
- Nallatamby C, Prigent M, Camiade M, Obregon JJ. Extension of the Leeson formula to phase noise calculation in transistor oscillators with complex tanks. IEEE Transact Microwave Theor Tech 2003; 51: 690-696.
- Ohira T. Rigorous Q-factor formulation for one- and two-port passive linear networks from an oscillator noise spectrum viewpoint. IEEE Transact Circuits Syst II 2005; 52: 846-850.
- Minami T, Ohira T. Unified activeQfactor formula for use in noise spectrum estimation from Leeson’s and Hajimiri’s models. IEICE Elect Express 2013; 10: 1-6.
- Ohira T. Extended Adler's injection lockedQfactor formula for general one- and two-port active device oscillators. IEICE Elect Express 2010; 7: 1486-1492.
- Huang XH, Tan F, Wei W, Fu W. A revisit to phase noise model of leeson. IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, 2007.