Research Article - Biomedical Research (2017) Volume 28, Issue 9
Simplified real-time heartbeat detection in ballistocardiography using a dispersion-maximum method
Sun-Taag Choe and We-Duke Cho*Graduate School of Electronics Engineering, Ajou University, Suwon 443-749, Korea
- *Corresponding Author:
- We-Duke Cho
Graduate School of Electronics Engineering
Ajou University, Korea
Accepted on January 31, 2017
Abstract
Ballistocardiography (BCG) enables the recording of heartbeat, respiration, and body movement data from an unconscious human subject. In this paper, we propose a new heartbeat detection algorithm for calculating heart rate (HR) and heart rate variability (HRV) from the BCG signal. The proposed algorithm consists of a moving dispersion calculation method to effectively highlight the respective heartbeat locations and an adaptive heartbeat peak detection method that can set a heartbeat detection window by automatically predicting the next heartbeat location. To evaluate the proposed algorithm, we compared it with other reference algorithms using a filter, waveform analysis and envelope calculation of signal by setting the ECG lead I as the gold standard. The heartbeat detection in BCG should be able to measure sensitively in the regions for lower and higher HR. However, previous detection algorithms are optimized mainly in the region of HR range (60~90 bpm) without considering the HR range of lower (40~60 bpm) and higher (90~110 bpm) HR. Therefore, we proposed an improved method in wide HR range that 40~110 bpm. The proposed algorithm detected the heartbeat greater stability in varying and wider heartbeat intervals as comparing with other previous algorithms. Our proposed algorithm achieved a relative accuracy of 98.29% with a root mean square error (RMSE) of 1.83 bpm for HR, as well as coverage of 97.63% and relative accuracy of 94.36% for HRV. And we obtained the root mean square (RMS) value of 1.67 for separated ranges in HR.
Keywords
Ballistocardiography, Real-time heartbeat detection, Moving dispersion calculation, Adaptive peak detection.
Introduction
Traditionally, certain machines have enabled unconscious sleep state tracking. One technology classifies the subject’s state as awake or asleep according to measurements of the subject’s movement from a motion sensor worn on the wrist [1]. Another technology measures the amount of sleep apnea or occurrences of snoring from recorded audio [2]. Ballistocardiography (BCG) is a third technology that measures the ballistic signal recorded through the subject’s bed during rest and sleep for analysis based on detected respiration, heartbeat, and physical movement [3]. The study presented here focuses on the detection of the subject’s heartbeat to estimate the subject’s heart rate (HR) and heart rate variability (HRV).
In general, the procedure for extracting the HR from the BCG signal is roughly classified into two steps [3]. The first step is to extract the heartbeat signal by pre-processing the signal to separate the heartbeat from respiration and extraneous noise. The second step is a peak detection process for detecting the exact position of the heartbeat from the processed signal. To calculate only the average HR, the main frequency of the HR is determined by a frequency analysis method (e.g., Fourier and wavelet), instead of the peak detection method. Frequency analysis methods usually detect the frequency with the biggest amplitude to calculate the average HR. To more accurately detect the heartbeat location, additional information including HRV is required, which is more relevant to predictions of possible sleep disorders than the HR [4].
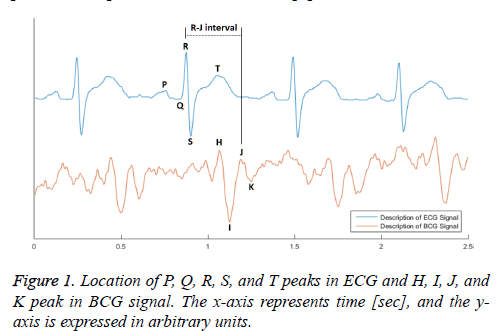
The BCG signal is a vibro-signal that is generated by movement of heart components such as the systole and diastole. In general, the heartbeat in BCG is indicated by a weight change of approximately 7 mg, and its frequency range is less than 40 Hz. In the BCG signal, the heartbeat waveform is defined by the description of the QRS Complex from the ECG. The J-peak in the BCG signal, from among the H, I, J, and K peaks shown in Figure 1 corresponds to the R-peak in the ECG [5]. The J-peak typically has the largest amplitude among the other BCG signal peaks. However, the BCG signal includes a wide variety of disturbance components, such as noise in the high frequency band occurring in the measuring device, as well as components caused by breathing in the low frequency band of 10-30 bpm. The signal is even affected by the properties of the mattress, whether the subject is wearing clothes, and the subject’s other physical characteristics. Therefore, the H-peak or I-valley frequently appears to be more prominent than the J-peak.
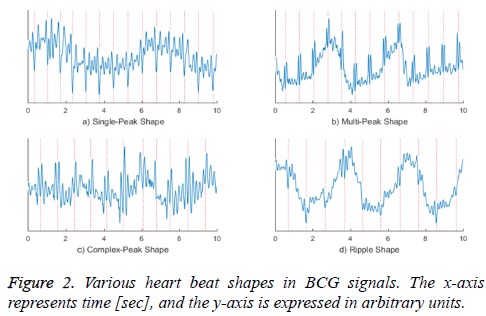
Figure 2 shows various shapes of actual measured BCG waveforms. The graph a) shows a shape in which the I-valley is bigger than others, and the graph b) shows a multi-peak shape, in which both the H- and J-peaks are large. The waveform in the graph c) is a complex form that shows either a single- or double-peaked heartbeat. The graph d) presents a shape in which the amplitude change of the heartbeat is slightly larger than a neighbouring noise signal, and therefore appears as a ripple. As discussed above, the waveform of the heartbeat can have various shapes even from the same sensor and subject and in the same acquisition environment.
The objective of this study is to extract consistent features of a BCG signal showing a variety of heartbeat shapes using a single signal processing technique. An algorithm is proposed based on a moving dispersion calculation method that can extract the heartbeat signal, even when it is distorted by noise or respiratory components. First, we analysed the waveforms of many heartbeats over observed distortion, and we found common features in many distorted heartbeat signals. The heartbeat signal can be influenced by the small amplitudes of high frequency signals, such as noise, and the large amplitudes of smaller frequency signals such as the inhalation and exhalation of respiration. The heartbeat waveform affected by the other components is observed to have amplitude that is larger than normal (when adding amplitudes) and a frequency that is higher than normal (when subtracting amplitudes). To develop the algorithm, we defined the change as increasing in the vicinity of the heartbeat measured in two cases, and we computed the amount of change in the signal using a moving dispersion calculation method.
In Section II, we briefly describe the BCG signal acquisition system and the various heartbeat waveforms acquired by BCG. Section III details the proposed algorithm, and Section IV presents an evaluation of the method. Finally, we discuss the results of this study in the last section.
Related Works
In previous studies, the heartbeat signal extraction method has been accessed using various methods. One method uses a band-pass filter and a combination of high-pass and low-pass filters to remove the respiratory and noise signals [6]. The most successful methods increase the amplitude swing (e.g., by squaring or cubing) of the band-pass filtered signal, and then apply low-pass filtering to the amplified signal [3,7].
Signals extracted by this amplification method have shown good performance when the HRV is stable [3]. However, subjects exhibit different differences in HR during rest and sleep depending on their physical ability [8]. Ordinary HRs range between approximately 50 and 100 beats per minute (bpm) in accordance with the subject's health, and sometimes, extraction methods using these filters which passes specific frequency do not cover the full HR range. Furthermore, although HRV may be stable, the filtering methods are not always able to remove respiratory signals sufficiently when respiration changes suddenly.
For effective noise cancelling, some algorithms have emerged to analyse the BCG signal in the frequency domain. Some studies [9,10] have tried to obtain a representative HR frequency in a converted frequency domain using Fast Fourier Transform [11] or Wavelet Transform [12]. Other studies have tried to detect the subject’s heartbeat in a cestrum signal that consists of the main frequencies of the HR [13-16]. This approach is appropriate for calculating the average HR. However, because it is difficult to determine the exact location of a HR, the HRV calculated in this way can be inaccurate [4].
In [17-20], the shape of the heartbeat was analysed more directly. These researchers extracted the features of the heartbeat signal from characteristics of the heartbeat’s shape in a signal in which the heartbeat was mixed with respiration and noise components. The heartbeat signal was characterized by having amplitude larger than the noise and smaller than the respiration signal. In addition, heartbeat signals often exhibited higher frequencies than the noise. To extract these features, an optimized model of the heartbeat’s shape is extracted from the BCG [21] or otherwise defined [22], and the heartbeat’s location in the recorded signal is decided by comparison with the model. When each heartbeat shape can be assumed to be relatively constant, the detection accuracy is very high. However, for different subjects or situations (such as posture or sleep state), the optimized model must be recalculated, and distinguishing cases with no heartbeat is difficult.
Several previous works have calculated a signal envelope [23] based on the higher frequency of the heartbeat compared to the respiratory signal [24-29]. The methods of computing this envelope include empirical mode decomposition [24], Hilbert transform [25], auto-correlation function [26,27], and moving maxima calculation [28,29]. These methods extract reliable heartbeat signals from irregular HRs because they do not overly smoothen the BCG signal. Nevertheless, the signal envelope is affected by large impulse signals (caused by breath or movement under normal conditions) because of the long duration of the previous state’s influence on the calculation.
Furthermore, these methods occasionally fail to detect the heartbeat when the heartbeat’s waveform appears to ripple because of a high frequency with no change in amplitude. Table 1 briefly describes these heartbeat signal extraction methods.
| Heartbeat Extraction Methods | Previous work | Discription |
|---|---|---|
| Band-pass Filter (including High → Low) Band-pass Filter → Squaring → | [6], [3,7] | Respiratory and noise signal canceling based on frequency domain |
| Low-pass Filter | ||
| Fast Fourier Transform Analysis | [9,10] | Heartbeat signal extraction based on frequency analysis |
| Adaptive Wavelet Cepstrum Analysis | [13-16] | |
| Heartbeat Shape Characteristic Analysis | [17-20] | Analysis based on shape of heartbeat waveform |
| Cross-correlation and Euclidean Distance | [21] | |
| Convolution Calculation | [22] | |
| Empirical Mode Decomposition | [24] | Signal envelope based on shape analysis |
| Hilbert Transform | [25] | |
| Auto-correlation Function | [26,27] | |
| Moving Maxima Calculation | [28,29] |
Table 1. Heartbeat signal extraction methods in previous works.
Methods of analyzing the relative shape of the heartbeat by contrasting it with nearby signal components (including noise peaks) are suitable for HRs with an irregular period. However, it is difficult to extract consistent features from an irregular shape. Actually, measurement systems confirm that the shape of the heartbeat waveform can be different even for the same posture and the same subject because the heartbeat waveform is frequently affected by random noise and changes in the amplitude and frequency of respiration.
Explanation of BCG Acquisition Process
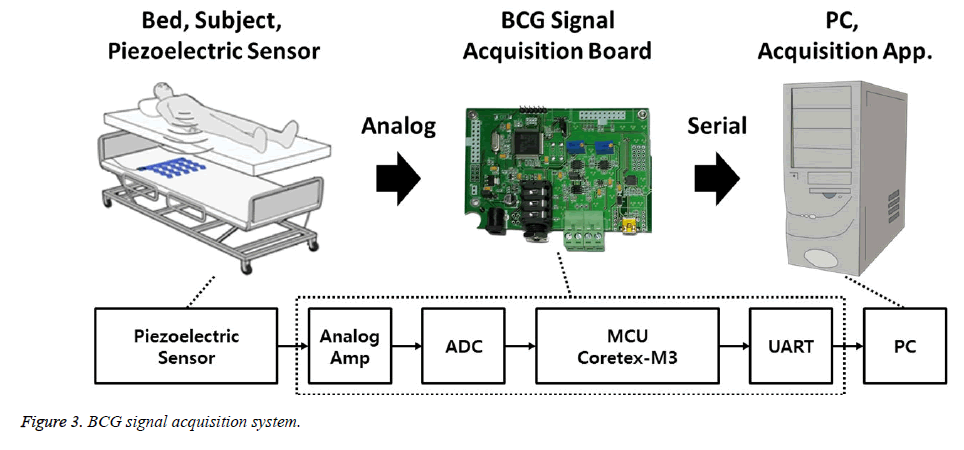
Figure 3 shows the BCG signal acquisition system. We installed the piezoelectric sensor (Bed Sensor L-4060SL, Emfit, Finland) between the bedframe and the mattress, such that the sensor was located under the subject’s back. The sensor signals were acquired from a second-order differential amplifier (TLV2772CP) using an analog-to-digital converter (Cortex-M3, ARM), with a 12-bit resolution and 100 samples per second (S/s). To evaluate the heartbeat location, the BCG signal was synchronized, with the ECG signal, which was recorded with 250 S/s.
We acquired the synchronized signal from 7 male subjects (23-28 years old) for the purpose of comparing the proposed algorithm with other previous algorithms and computing general statistical performance metrics. The recorded signals were acquired three times for each subject, with at least 15 min in which the subject was not moving. However, we lost two data sets because of an ECG acquisition error, and therefore we acquired 19 data sets. The recorded signals were sufficient to evaluate the performance of the proposed algorithm because the recorded signal lengths totalled more than 5 h and included a HR range of approximately 47 to 106 bpm.
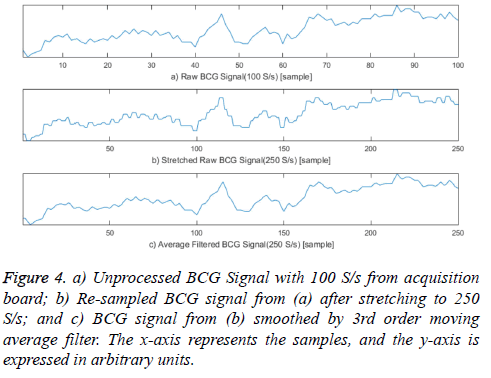
The BCG signal acquired with 100 S/s was stretched to 250 S/s by duplicating each original sample 2 or 3 times to compare the exact heartbeat locations. A square wave was generated when the signal was stretched; therefore, the stretched BCG signal was smoothed by a 3rd order moving average filter because these square waveforms can create unnecessary components in the frequency domain, affecting previous algorithms based on signal frequencies. Figure 4 presents these pre-processing steps for comparing the location of heartbeats in the acquired BCG and ECG signals. This pre-processing can be ignored when implementing the proposed system because the procedure is only necessary for evaluating our proposed algorithm.
Dispersion-Maximum Algorithm
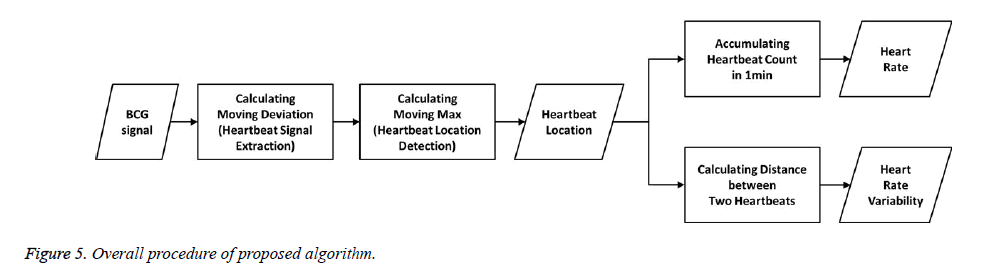
In the BCG signal, different types of heartbeat waveforms can be distinguished by local maxima (peak) or minima (valley) of the waveform, and may exhibit more high frequency vibrations than noise components of the waveform. Therefore, the various features of heartbeat waveforms disguised by various noises must be discovered by a signal processing algorithm. To obtain a common feature of these various heartbeat waveforms, we propose a method for computing a moving dispersion calculation. The algorithm is executed in two parts. First, the moving dispersion signal is extracted to distinguish it from the location of the heartbeat waveform on the BCG signal. Next, the more exact heartbeat location is detected in the moving maximum of the signal, which has an adaptive window size extracted from the heartbeat signal. The detected heartbeats are accumulated for 1 min to compute the HR, and we calculated the interval distance between the two nearest heartbeats to compute the HRV. Finally, the calculated HR and HRV are used to evaluate the performance of our proposed algorithm in comparison with previous methods.
Heartbeat Signal Extraction
We calculate the moving dispersion signal to extract a clearer location of each heartbeat. The moving dispersion signal is computed in a similar manner to that of a moving average. Dispersion is a value indicating how much the values of the data deviate from each other, also known as variability, scatter or spread. Dispersion can be calculated from variance, standard deviation, mean absolute deviation, or interquartile range. When calculating the dispersion of the signal, two effects can be obtained. The first is the effect of removing the breathing component of the low frequency band according to the window size. The second is the effect of further emphasizing the instantaneous amplitude vibration. Therefore, the moving dispersion method is effective when the heartbeat interval changes because this method focuses more on the vibration of the heartbeat waveform than the frequency of heartbeats.
We implemented our algorithm using the mean absolute deviation method, which imposes less calculation burden than the other dispersion calculation methods. In particular, the computing of absolute value can be replaced by a bit-wise operation, enabling the proposed algorithm to reduce the calculation burden compared with variance and standard deviation computing.
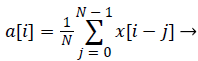 (1)
(1)
a: Moving Average
N: Sliding Window Length
x: BCG Signal
i: Sequence
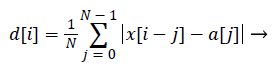 (2)
(2)
d: Moving Mean Absolute Deviation
N: Sliding Window Length
a: Moving Average
x: BCG Signal
i: Sequence
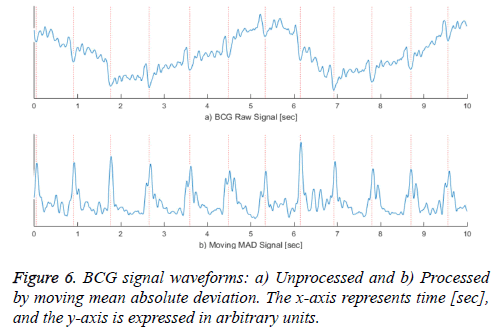
Equation (1) is a general function for computing a moving average and equation (2) is a formula for computing a moving mean absolute deviation signal. In equations (1) and (2), x is the recorded BCG signal, a is the computed moving average value, and d is the computed moving mean absolute deviation value, which has a window size N at the i'th iteration. The window size N is calculated by multiplying the sampling rate and the sliding window time. Because the heartbeat waveform that appears in the BCG signal has a period between approximately 0.05 and 0.1 s, we set a window time of 0.05 s for the minimum length of the heartbeat waveform in the stretched signal (250 S/s). Therefore, the window time length N is designed to be 12 sequences. To extract a signal having a longer period, such as respiration, N can be set to be higher. In addition, because dispersion is calculated from at least two values, the value of N should be greater than one. The graph a) in Figure 6 shows the unprocessed BCG signal. When equation (1) is applied, the heartbeat location is highlighted, as shown in the graph b). In Figure 6, the vertical dotted lines in both graphs indicate the I-valley locations of the heartbeat waveform that is the final target of our proposed method. The graph b) confirms that the heartbeat location is clearly calculated, and low frequency components from respiration are removed.
Heartbeat Peak Detection
We propose a peak detection method based on the adaptive moving maximum signal to detect the exact location of the heartbeat in the case that the heartbeat interval cycle changes from the calculated moving mean absolute deviation signal. In general, heartbeat detection methods detect heartbeat peak candidates by an adaptive thresholding technique that determines the largest peak in a specific region, and then removes neighbouring small peaks in that region [3]. With this method, the specific region is set to be 0.4 s based on the averaged HR. The operation by which the extra peaks are removed is rather complicated because the process traces the signal recursively.
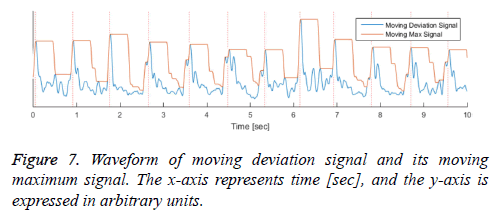
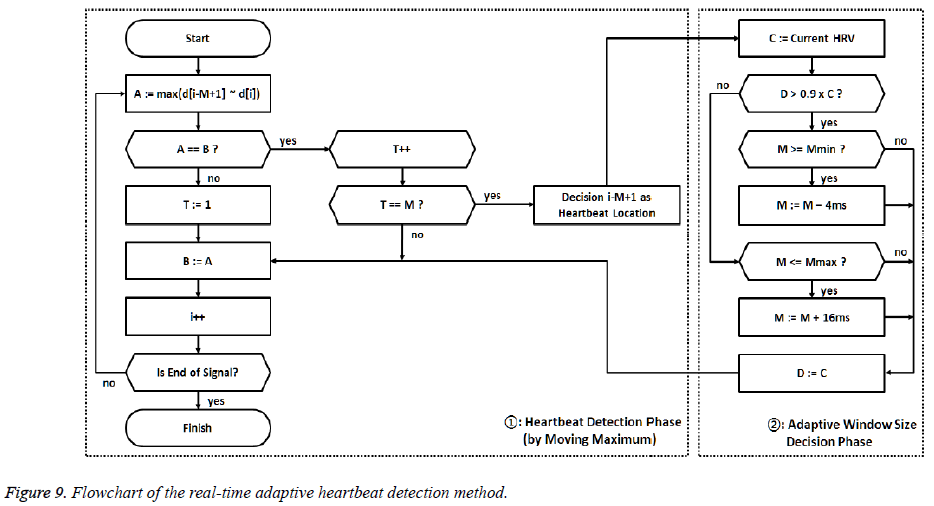
We propose a method for peak detecting that applies the specific region before detecting the heartbeat peak. Our proposed algorithm calculates the moving maximum value and detects the heartbeat based on the times at which the maximum value is reached. This peak detecting method imposes less calculation burden than the method that removes extra peaks after detecting candidate peaks. The following equation (3) is the formula for calculating the moving maximum signal. In equation (3), the signal m is moving maximum signal derived from the moving mean absolute deviation signal d calculated from equation (2), with the sliding window length M.
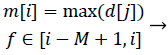 (3)
(3)
d: Moving Mean Absolute Deviationc
m: Moving Maximum
M: Sliding Window Size
i: Sequence
At this time, we set M = 100 because the initial time region of 0.4 s. This is related to the range of heartbeat-to-heartbeat intervals, which is approximately 0.5 to 1.5 s.
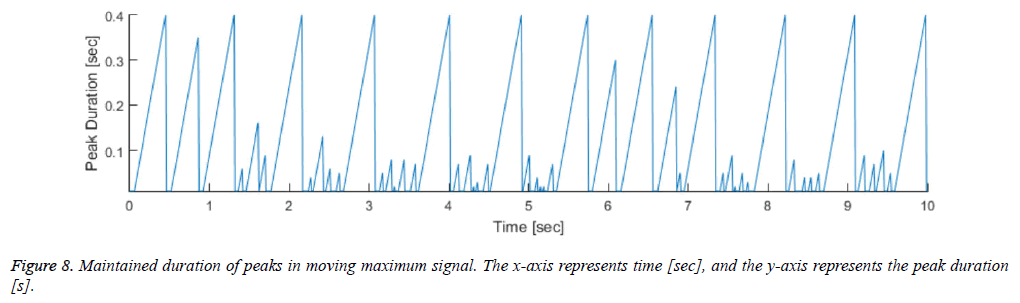
The moving maximum signal m of equation (3) forms an upper envelope of the moving mean absolute deviation signal d in Figure 7. The peak signal in the generated upper envelope is flat and is maintained for the duration of the window size M. Our algorithm determines that each of the starting peak points in the signal d is a heartbeat point, and maintains each maximum value for the duration of the window size M. The method of calculating the holding time of the maximum value is designed to be a timer for equation (4). The value m in equation (4) is the moving maximum value from equation (3), and the value t is a timer value that is initialized when m is changed and increases as long as m is maintained. Therefore, t represents the duration for which the largest peak in a specific region is maintained, described by a saw-tooth waveform, as shown in Figure 8. If the holding time t reaches M, the largest
peak is detected as the heartbeat. The value b in equation (5) is 1 when the heartbeat is detected and is 0 when the heartbeat is not detected. Because the location of the heartbeat is calculated after the size of the sliding window M, the position of the detected heartbeat sequence is i - M + 1 when b[i] is 1.
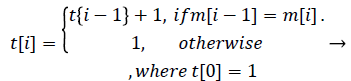 (4)
(4)
m: Moving Maximum
t: Timer
i: Sequence
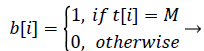 (5)
(5)
t: Timer
M: Sliding Window Size
i: Sequence
In addition, we applied the method of adaptive controlling to the sliding window size M. This method increases or reduces M by comparing the distance between the current and previous HRVs. We determined appropriate operating parameters by various simulations that are standard for this purpose. If the current HRV interval was greater than the previous by 90%, the sliding window size increased 16 ms; when the current HRV interval was less than the previous by 90%, the sliding window size reduced 4 ms. In this way, when the HRV lessened, the peaks were detected in the shorter region, and when the HRV increased, the longer region was applied. We limited the minimum size of the sliding window to 0.3 sec and the maximum size to 0.5 sec to prevent the value of M from deviating outside the general HR range.
The Figure 9 shows a flowchart for the proposed peak detection method in real time. In the flowchart, d is the moving mean absolute deviation signal from equation (2), T is the timer value from equation (4), and M is the length of the sliding window. In addition, Mmax (0.5 sec) and M min (0.3 sec) are the maximum and minimum limits of the M value, respectively; A and B are buffers that store the values of the moving maximum signal; and C and D are buffers that store the value of the HRV. The flowchart is largely divided into two stages. The first stage represents the process of performing equations (3) through (5) to detect the heartbeat sample by sample. The second stage includes the determination of the sliding window size M for adaptively calculating the moving maximum signal. In this stage, the next detecting region is decided by the relative ratio of the current HRV to the previous HRV.
Performance evaluation
Performance metrics: We used the ECG lead I synchronized with the BCG signal to calculate the HR and HRV by an algorithm currently in use as a gold standard for comparison with our proposed method. The R-peak in the acquired ECG signal, synchronized with the BCG signal, was detected by the adaptive peak detection method presented in [30]. We compared the R-R interval from the R-peaks detected with this reference algorithm and the J-J interval detected with our proposed algorithm, as well as the two HR values.
The HRs from both the ECG and BCG are calculated from the heartbeat count accumulated in 1 min, with each signal overlapping by 59 s. Some cases compare the heartbeat count from the entire recorded signal; however, these comparisons are often inaccurate because this method obtains both false positive and false negative results in units of 1 min. We computed the relative accuracy using equation (6) and the root mean square error (RMSE) from equation (7). In equation (6), HRECG is the HR from the ECG, and HRBCG is either the calculated HR from our algorithm or from the reference algorithm. The value K is the number of HR samples dependent on the measured data set from the subjects.
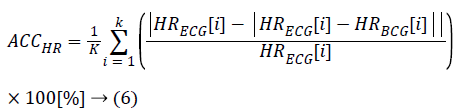
HRECG: Measured Heart Rate from ECG
HRBCG: Estimated Heart Rate from BCG
K: Count of HR (every second) in Each Data Set
ACCHR: Relative Accuracy of HRBCG
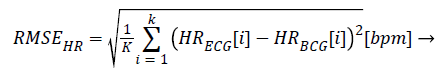 (7)
(7)
HRECG: Measured Heart Rate from ECG
HRBCG: Estimated Heart Rate from BCG
K: Count of HR (every second) in Each Data Set
RMSEHR: Root Mean Square Error between HRECG and HRBCG
To calculate the HRV, we checked the heartbeat from the BCG corresponding to every R-peak on the ECG signal. Because the heartbeat in the BCG always appears later than the R-peak in the ECG, the first heartbeat detected after the R-peak was selected; if there is no detected heartbeat after the R-peak, this situation is considered to be an error. The estimation range of each algorithm is called the coverage. We calculate the coverage as the percentage of the total detected heartbeat counts over the total number of R-peaks. A higher coverage indicates that the algorithm is more stable. Furthermore, we evaluated the proposed algorithm by substituting the R-R interval and the heartbeat interval from the BCG into equation (6) to calculate the proposed algorithm’s relative accuracy.
Performance of reference algorithm: The pre-processing methods of extracting the heartbeat in the BCG signal presented in the previous studies were applied in several different ways in those studies. Our comparison is based on a representative of these methods. The methods based on frequency analysis in the previous works are not suitable for detecting the heartbeat in real time. Therefore, the most accurate methods for extracting the heartbeat were selected from among the methods using filters, heartbeat waveform models, and envelope calculating. Each heartbeat extracting method was simulated based on its optimal parameter values, and the Butterworth filter was applied from the previous algorithm for pre-processing.
The first representative method that uses filters is proposed in [7]. This method calculates an appropriate band-pass filtered signal and then removes noise by squaring the band-pass filtered signal to amplify the heartbeat waveform with a lowpass filter. To estimate the optimal result from the recorded BCG signal, we set the cut-off frequency of the band-pass filter at 10 to 30 Hz, and we set the cut-off frequency of the low-pass filter at 10 Hz.
The second representative is proposed in [22], in which the heartbeat is modeled using a sinusoidal waveform. The heartbeat signal was calculated by combining this sinusoidal model with a bandpass filtered BCG signal. The optimal cutoff frequency of the band-pass filter is 10 to 40 Hz. The heartbeat model described in [22] is a sinusoidal model with a time duration of 0.33 s. Therefore, the sequence length of this model is 83 iterations when the signal is stretched to 250 S/s. Lastly, we implemented the method presented in [28]. This method calculates the envelope of the BCG signal using a moving maximum signal with a sliding window time of 0.25 s. The method also applies a band-pass filter to cancel noise; the optimal cut-off frequency of this band-pass filter is 5 to 20 Hz.
All of these previous methods demonstrate excellent performance and have offered significant contributions to the field. Each previous study included post-processing steps to refine the detected heartbeat. However, in this study, we evaluated our algorithm and others without applying the post process method to compare only the heartbeat signal extraction method.
Results
Table 2 shows the relative accuracy and the RMSE for the HRs calculated by both the proposed and reference algorithms. Our proposed method estimated the HR with a slightly higher accuracy (98.29%) than others, and estimated the HRV with a lower RMSE (1.83 bpm) than others. And the obtained standard deviation of accuracy (=0.56) is the smallest against compared algorithm. From the RMSEs shown in Table 2, although the estimations from our algorithm did not exhibit the highest accuracy in all data sets, our algorithm produced estimations with a consistent accuracy.
| # of Data Set |
Record Time [mm:ss] |
ACCHR [%] | RMSEHR [bpm] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| [7] | [22] | [28] | Proposed | [7] | [22] | [28] | Proposed | ||
| 1 | 14:02 | 97.73 | 95.64 | 97.71 | 97.89 | 3.19 | 6.47 | 2.67 | 2.84 |
| 2 | 21:52 | 99.36 | 99.23 | 98.76 | 98.51 | 0.87 | 0.9 | 1.43 | 1.7 |
| 3 | 16:23 | 99.35 | 99.3 | 97.97 | 97.94 | 0.85 | 0.81 | 1.97 | 2.04 |
| 4 | 14:06 | 91.85 | 99.23 | 94.47 | 97.93 | 5.06 | 0.97 | 3.5 | 1.45 |
| 5 | 14:35 | 97.39 | 98.49 | 96.48 | 98.99 | 1.88 | 1.36 | 2.49 | 0.85 |
| 6 | 17:33 | 94.21 | 97.49 | 90.99 | 97.75 | 3.72 | 1.69 | 5.45 | 1.78 |
| 7 | 20:43 | 95.69 | 98.47 | 91.7 | 98.06 | 2.91 | 1.13 | 5.21 | 1.43 |
| 8 | 17:06 | 98.16 | 97.98 | 98.5 | 98.95 | 1.59 | 1.66 | 1.23 | 0.92 |
| 9 | 14:20 | 98.76 | 99.07 | 99.03 | 98.89 | 1.09 | 0.86 | 0.91 | 1.02 |
| 10 | 14:37 | 99.27 | 99.71 | 99.23 | 98.35 | 0.8 | 0.47 | 0.82 | 1.62 |
| 11 | 14:22 | 99.46 | 99.14 | 98.81 | 98.65 | 0.64 | 0.98 | 1.17 | 1.33 |
| 12 | 14:49 | 98.84 | 98.68 | 99.25 | 99.07 | 1.34 | 1.41 | 0.87 | 0.92 |
| 13 | 14:43 | 98.57 | 97.05 | 98.1 | 97.78 | 1.33 | 2.81 | 2.17 | 2 |
| 14 | 14:19 | 99.67 | 99.03 | 98.74 | 98.85 | 0.54 | 1.19 | 1.32 | 1.28 |
| 15 | 21:13 | 98.24 | 97.02 | 98.37 | 98.44 | 2.52 | 4.4 | 2.81 | 1.98 |
| 16 | 16:13 | 98.93 | 97.78 | 98.83 | 96.97 | 1.37 | 2.35 | 1.4 | 3.7 |
| 17 | 16:10 | 98.94 | 95.26 | 98.74 | 98.23 | 1.36 | 6 | 1.71 | 2.14 |
| 18 | 17:07 | 98.2 | 99.12 | 97.74 | 97.67 | 1.77 | 0.92 | 2.08 | 2.09 |
| 19 | 21:36 | 98.69 | 99.23 | 97.85 | 98.65 | 1.22 | 0.81 | 1.93 | 1.31 |
| Mean | 16:37 | 97.97 | 98.27 | 97.35 | 98.29 | 2.12 | 2.57 | 2.6 | 1.83 |
| St.Dev | 2:45 | 2 | 1.27 | 2.42 | 0.56 | _ | _ | _ | _ |
ACCHR[%]:Relative Accuracy of HRBCG; RMSEHR [bpm]: Root mean square error between HRECG and HRBCG; St. Dev: Standard deviation.
Table 2. Performance of proposed and other methods for HR.
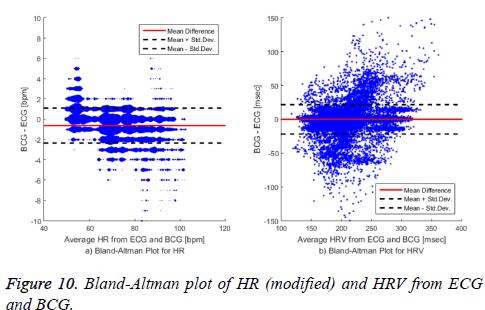
The HR distributions are different in each data set. In particular, some data sets had an average HR of over 100 bpm, and there were some data sets that had an average HR of approximately 50 bpm. Table 3 shows the evaluation results for the HRV calculation. The proposed algorithm measured the HRV with a similar accuracy to that of the reference algorithms. Evaluating the coverage of the HRV was somewhat different than evaluating the accuracy of the HR because we evaluated the HRV calculation based on the first heartbeat from the BCG appearing after each R-peak in the ECG. The reason for the difference between our proposed algorithm and that of [28] regarding the HR accuracy and the HRV coverage indicates that the algorithm in [28] overestimated the calculation relative to ours. Figure 10 presents a Bland-Altman plot of the HR and HRV calculated with our algorithm. The HR is measured in natural numbers, and therefore the difference in the HR values from the BCG and the ECG does not show a continuous form. We modified the Bland-Altman plot of the HR in graph a) by representing the size of each dot according to the number of points overlapping at the given location. Comparing our proposed algorithm with the combined reference algorithms representing the gold standard, the averaged HR error was -0.63 bpm and the standard deviation was 1.72 bpm.
Table 4 shows the averages and standard deviations of the error of each respective algorithm. When comparing the average of the error, it appears that our algorithm showed lower performance than others; however, our algorithm showed the lowest standard deviation of error among the implemented algorithms. Therefore, our proposed algorithm calculates less overestimation or underestimation than the other algorithms.
| # of Data Set |
Count of R-R Intervals |
COVHRV [%] | ACCHRV [%] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| [7] | [22] | [28] | Proposed | [7] | [22] | [28] | Proposed | ||
| 1 | 1404 | 97.69 | 94.49 | 97.62 | 97.91 | 96.6 | 98.1 | 97.88 | 97.5 |
| 2 | 1752 | 90.2 | 99.23 | 95.03 | 98.65 | 95.55 | 97.68 | 95.43 | 96.57 |
| 3 | 872 | 97.34 | 99.62 | 93.77 | 88.62 | 94.56 | 97.12 | 92.16 | 94.46 |
| 4 | 732 | 99.2 | 88.75 | 98.53 | 99.59 | 96.64 | 97.4 | 94.13 | 95.53 |
| 5 | 576 | 95.82 | 99.88 | 84.77 | 91.57 | 91.17 | 91.7 | 84.97 | 91.97 |
| 6 | 638 | 96.64 | 99.69 | 97.48 | 86.92 | 90.56 | 93.14 | 91.57 | 93.67 |
| 7 | 1146 | 99.82 | 100 | 99.8 | 99.74 | 91.86 | 95.65 | 94.14 | 95.16 |
| 8 | 1148 | 98.91 | 98.12 | 99.73 | 99.74 | 90.98 | 91.18 | 96 | 96.42 |
| 9 | 1006 | 99.7 | 99.7 | 99.8 | 99.31 | 88.45 | 92.76 | 92.22 | 94.32 |
| 10 | 1096 | 99.55 | 88.54 | 99.82 | 98.74 | 90.7 | 94.73 | 93.66 | 90.58 |
| 11 | 1039 | 95.71 | 90.92 | 99.52 | 98.95 | 90.52 | 92.82 | 95.31 | 91.7 |
| 12 | 1115 | 99.08 | 98.99 | 99.25 | 98.24 | 93.5 | 96.14 | 96.36 | 97.15 |
| 13 | 1042 | 98.68 | 96.55 | 98.5 | 97.84 | 84.55 | 86.95 | 88.93 | 87.58 |
| 14 | 1161 | 99.18 | 94.41 | 92.48 | 99.06 | 95.51 | 96.54 | 90.68 | 94.41 |
| 15 | 1943 | 98 | 91.71 | 98.18 | 98.33 | 94.17 | 95.33 | 93 | 93.96 |
| 16 | 1333 | 96.21 | 93.96 | 96.82 | 96.8 | 93.5 | 93.96 | 92.52 | 93.27 |
| 17 | 1447 | 99.12 | 91.95 | 98.71 | 98.44 | 95.03 | 94.23 | 95.52 | 96.41 |
| 18 | 1213 | 97.92 | 99.53 | 96.38 | 97.27 | 92.62 | 93.25 | 89.03 | 93.94 |
| 19 | 1515 | 99.27 | 99.48 | 98.62 | 98.95 | 91.12 | 92.67 | 89.13 | 94.36 |
| Mean | 1167 | 97.67 | 95.91 | 97.4 | 97.63 | 92.77 | 94.47 | 93.08 | 94.36 |
| St,Dev | 350 | _ | _ | _ | _ | 3.02 | 2.74 | 3.2 | 2.44 |
COVHRV[%]: HRV coverage of each algorithm; ACCHR[%]:Relative Accuracy of HRBCG;St.Dev: Standard Deviation
Table 4. Difference of HR Estimated by proposed and reference methods from ECG.
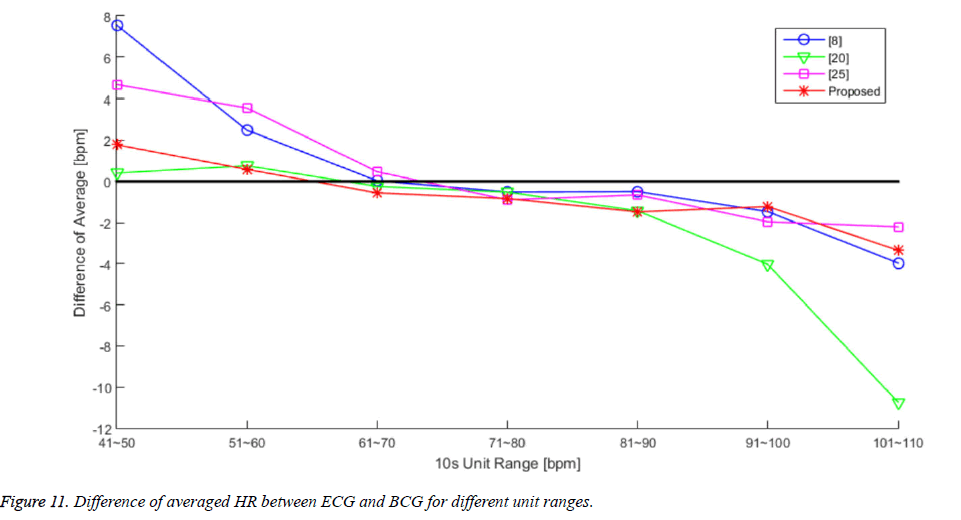
We attempted to calculate the performance results for each algorithm according to each region of the HR range. Figure 11 and Table 5 present the averaged HR error for each algorithm in 10 unit increments. There is an overall trend of overestimation in the lower HR range and an underestimation trend in the higher HR range. The algorithms from [7] and [28] calculated larger differences in the lower HR range, and the algorithm from [22] calculated a larger difference in the higher HR range. However, the proposed algorithm exhibited stable differences in both the lower and higher HR ranges, compared to the other algorithms.
| [7] | [22] | [28] | Proposed | |
| Average of Error [bpm] | 0.18 | -0.77 | 0.33 | -0.63 |
| Standard deviation of error [bpm] | 2.11 | 2.45 | 2.57 | 1.72 |
Table 5. The Values of Each Difference of Averaged HR Plot in Figure 11.
Although, our proposed algorithm cannot achieve the highest accuracy in each separated HR range, the error of [7] and [28] is more 3 times than [22] and the proposed algorithm in lower HR range (41~60 bpm), and the error of [22] is more 2 times than other compared algorithm including ours in higher HR range (91~110 bpm). The compared algorithms that used in evaluation cannot detect heartbeat in varying heartbeat intervals for lower or higher HR ranges, because they are optimized with averaged HR range (61~90 bpm) [4]. However the performance of the proposed algorithm was nearly stable in wide range in HR (41~110 bpm). As RMS values show in Table 5, our algorithm has the lowest value against the other algorithms. Since an adaptive heartbeat detection method of the proposed algorithm is applying the changing window size method based on calculated heartbeat intervals, it works more sensitively in wide heartbeat detecting interval.
Conclusion
The method proposed in this study extracts the heartbeat signal using a moving dispersion calculation and detects the heartbeat using an adaptive moving maximum calculation that depends on the previously detected heartbeat location. We confirmed the stable performance of this estimation in a variety of HR ranges; therefore, our proposed method is considered to be more stable in various ranges than other reference methods even though its accuracy is not outstandingly high. However, the proposed signal processing method requires further mathematical analysis. The proposed method does not completely eliminate the specific region used in the frequency response analysis, as with the moving average filter, and the proposed method imposes other effects such as removing lowfrequency components of the frequency domain at the same time. In future research, we will analyse the meaning of the absolute value in the moving dispersion signal, rather than the relative waveform of this signal. In addition, during the experiment, we discovered differences in the heartbeat signal size relative to the breathing signal size in accordance with the physical condition of the subject, including factors such as weight, lean mass, and body fat. Therefore, in future research, we would like to apply the results of this study to infer cardiac performance based on the proposed moving dispersion signal.
References
- Mullaney DJ, Kripke DF, Messin S. Wrist-actigraphic estimation of sleep time. Sleep 1980; 3: 83-92.
- Cavusoglu M, Kamasak M, Erogul O, Ciloglu T, Serinagaoglu Y, Akcam T. An efficient method for snore/nonsnore classification of sleep sounds. Physiolmeasurem 2007; 28.8: 841.
- Jiang F, Song S, Cheng J, He S. A research based on BCG signal detection device. Atlant Press 2014.
- Elsenbruch S, Harnish MJ, Orr WC. Heart rate variability during waking and sleep in healthy males and females. Sleep 1999; 22: 1067-1071.
- Tolles, Walter E. Computer search for ballistocardiographic indices of cardiovascular disease. Signal Processing Systems Design and Implementation. IEEE 2005; 19: 126-135.
- Junnila S, Akhbardeh A, Värri A, Koivistoinen T. An EMFi-film sensor based ballistocardiographic chair: performance and cycle extraction method. Signal Process Syst Design Implement IEEE 2005.
- Friedrich D, Aubert XL, Führ H, Brauers A. Heart rate estimation on a beat-to-beat basis via ballistocardiography a hybrid approach. IEEE 2010.
- http://www.sportsscience.co/sport/good-resting-heart-rate-chart-reference-table/
- Watanabe K, Watanabe T, Watanabe H, Ando H, Ishikawa T, Kobayashi K. Noninvasive measurement of heartbeat, respiration, snoring and body movements of a subject in bed via a pneumatic method. IEEE Transact 2005; 2100-2107.
- Kimura H, Kobayashi H, Kawabata K, Der Loos HF. Development of an unobtrusive vital signs detection system using conductive fiber sensors. Intel Robo and Syst 2004; IROS 2004.
- James WC, Tukey JW. An algorithm for the machine calculation of complex Fourier series. Math of comput 1965; 19.90: 297-301.
- Yves M. Wavelets and operators, volume 37 of Cambridge Studies in Advanced Mathematics 1992.
- Zhu X, Chen W, Nemoto T, Kanemitsu Y, Kitamura K. Real-time monitoring of respiration rhythm and pulse rate during sleep. IEEE Trans Biomed Eng 2006; 53: 2553-2563.
- Postolache O, Girao P, Postolache G, Pereira M. Vital signs monitoring system based on emfi sensors and wavelet analysis. Instrumentation and Measurement Technology Conference Proceedings, 2007. IMTC 2007.
- Chen W, Zhu X, Nemoto T, Kitamura KI, Sugitani K, Wei D. Unconstrained monitoring of long-term heart and breath rates during sleep. Physiolmeas 29.2: IEEE. IEEE, 2007.
- Jin J, Wang X, Li S, Wu Y. A novel heart rate detection algorithm in ballistocardiogram based on wavelet transform. Knowledge Discovery and Data Mining IEEE, 2009
- Smrcka P, Jirina M, Trefny Z, Hana K. New methods for precise detection of systolic complexes in the signal acquired from quantitative seismocardiograph. Intel Signal Process IEEE, 2005.
- Mark B, Müller CH, Schierz C. Contact-free measurement of heart rate, respiration rate, and body movements during sleep. Behav Res method 2006; 511-521.
- Jaehyuk S, Chee Y, Park K. Long-term sleep monitoring system and long-term sleep parameters using unconstrained method. Intl Special Topic Conf. on Info. Tech. in BME, Ioannina-Epirus, Greece, 2006.
- Alireza A, Kaminska B, Tavakolian K. BSeg++: A modified blind segmentation method for ballistocardiogram cycle extraction. Engineering in Medicine and Biology Society, 2007.
- Brüser C, Stadlthanner K, de Waele S, Leonhardt S. Adaptive beat-to-beat heart rate estimation in ballistocardiograms. IEEE Trans InfTechnol Biomed 2011; 15: 778-786.
- Joonas P, Ranta M. Detecting heartbeats in the ballistocardiogram with clustering. Proceedings of the ICML/UAI/COLT 2008 Workshop on Machine Learning for Health-Care Applications, Helsinki, Finland. 2008; 9.
- Johnson Jr, Richard C, Sethares WA, Klein AG. Software receiver design: build your own digital communication system in five easy steps. Cambridge University Press, 2011.
- Nan B, Ueno N, Fukuda O. Monitoring of respiration and heartbeat during sleep using a flexible piezoelectric film sensor and empirical mode decomposition. IEEE, 2007.
- Phan DH, Bonnet S, Guillemaud R, Castelli E, Thi NP. Estimation of respiratory waveform and heart rate using an accelerometer. EMBS 2008.
- Aubert, Xavier L, Brauers A. Estimation of vital signs in bed from a single unobtrusive mechanical sensor: Algorithms and real-life evaluation. IEEE, 2008.
- Shin JH, Chee YJ, Jeong DU, Park KS. Nonconstrained sleep monitoring system and algorithms using airmattress with balancing tube method. IEEE Transactions on 2010; 147-156.
- Hwang SH, Yoon HN, Lee YJG, Jeong DU, Park KS. Nocturnal awakening and sleep efficiency estimation using unobtrusively measured ballistocardiogram. IEEE Transactions 2014; 131-138.