Research Article - Biomedical Research (2016) Computational Life Sciences and Smarter Technological Advancement
Scrambling algorithm for encryption of text using cube rotation artificial intelligence technique
Rajavel D1* and Shantharajah SP21Research Scholar, Science and Humanities, Anna University, Chennai, India
2Professor, SITE, VIT University, Vellore, India
Accepted on August 24, 2016
Abstract
This paper lead forward to a new approach of text scrambling algorithm for encryption using artificial intelligence technique of cubical text and its random rotation type with angle. At first the original message is converted into six face cubical form (3 × 3 × 3 cube) and the cube is chosen as it is easy to scramble the message in cubical form. Rotation types and angle of rotations are generated using random function which is used as an encryption key, randomness in the key make encryption stronger. There are 18 possible rotation types and each rotation can have any one of the 3 different rotation angles. Finally cube layers are rotated for 18 times in any of the three different angles by using the encryption key value. The cube layers rotated here are as same as the simple Rubik’s cube rotation. At the end of rotation, the original message cube is scrambled to give the unpredictable pattern. Random rotations used in this approach produce secure cipher text, which is unbreakable from cryptanalysis without the encryption key. Intention of this research is to provide secure and novel approach of artificial intelligence scrambling technique to the encryption field. In this algorithm we used cubical scrambling methods and novel way of representing text in cube format. Algorithm’s experimental result in each phase of scrambling is shown with comparative analysis of text position in cipher message with original message. Analysis of result shows that original message is scrambled and provided the secure and unpredictable message; hence the novelty of this Artifical intelligence scrambling approach is evidenced.
Keywords
Text scrambling algorithm, Rubik’s cube rotation, Cubical text, Cube rotation angle, Cube rotation types, Random sequence.
Introduction
Information transfer in web is indeed and exhibits remarkable growth now-a-days. Transferring the sensitive information is critical to a large extent in web and hackers can able to get the information without the knowledge of sender and receiver. Even though the data ceased by the hackers are not the original message which are encrypted using an encryption algorithms. Still, hacker can easily find the sensitive data and predict the cipher text. The main reason is that, hackers do their cryptanalysis on cipher text with different attacks even they does not know the key, attack can be done in many different way as mention by Iokibe et al. [1] and Patel et al. [2]. Hackers generate their own key to apply decryption on knowing cipher text. So, it is necessary to increase the key strength and key space to avoid easiest prediction of key. Thus key management is one of the main aspects in information security and it plays a major role in defining the strength of encryption Obukhov et al. [3]. To avoid the cipher attacks, key space should be increased, which make difficulties to predict the original message. Recently National Institute of Standards and Technology (NIST) at United State of America (USA) propose that the current RSA key length of 2048-bits should be discontinued before the year 2030 and need an increased key length for better security [4]. Security system must have secret method to avoid hackers foresee the pattern, randomness provide high security from the prediction of pattern. Randomness provide different behavior of result even when applying for same data, it makes difficulty in finding the key as well as original message by hackers. Even using of randomness in proper places makes sense to provide hardness of the data. In most of the cases, random number generation process is necessary for the encryption of any text or images as used by Zaverucha et al. [5] and Singla et al. [6]. In an advanced cryptographic system like RSA, Diffie Hellman’s, randomness plays a main role in generating the key.
In cryptography, text scrambling is method of encryption in which the positions held by original messages are scrambled according to the position replacement, so that the cipher text consists of permutation of original message. Scrambling text is mostly effective when working with fractionation. Kumar et al. [7] have used the scrambling technique but the arrangement of message was done in two dimensional spaces. This two dimensional space may not give more complication for hacker to cryptanalysis in comparison to the three dimensional and cubical space. In this approach it requires more number of row or column transformation to come up with better secure cipher text, it makes more time for encryption as well as decryption. Scrambling the image in two dimensional and three dimensional spaces to encrypt the image has also been studied in Diaconu et al. [8] and Gomathi et al. [9] research. Usage of image in scrambling and encryption provides good result in generating unpredictable pattern. The usage of the above mentioned scrambling technique using the text has been extensively studied and reported by us [10]. Briefly, we have used text scrambling approach via rotation square and the original message is formed in three dimensional arrays in that paper. The usage of text in our scrambling approach resulted in efficient variation in scrambling the original message. Li et al. [11] proposed the image scrambling via six face Rubik’s cube rotation, and it gave the good result of an encrypted image. This study encourages the proposed work in the usage of text in rotating as six face Rubik’s cube for scrambling the original message.
Purpose of this research is to provide secure and novel approach of Artificial intelligence scrambling technique to the encryption field. This present research, implements the text scrambling encryption algorithm based on generating random number sequence for rotating Rubik cubes. Cubical representation of message gives the novelty of the research and affords the new approach to the encryption technique. Cubical form of text is more reliable for scrambling algorithm, because single rotation of a cube scrambles the text in five out of six faces of a cube. Random number performs an important role in this approach to define the rotation type, where hacker cannot easily decrypt the cipher message without the key.
Basic Theorem
Rubik’s cube
Rubik’s cube was invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik. In Classic 3 × 3 × 3 Rubik’s cube have six faces with different colors in each face, when the 9 different pieces of all the six faces have same color then the cube is solved. Cube is solved by using 18 different rotations for classical Rubik’s cube. Number of rotation (NR) is possible rotation type
NR=3layer × 6faces=18 → (1)
Permutations of the original 3 × 3 × 3 Rubik's Cube is like to be 8! × 38 × (12! × 2) × 211
which is approximately forty-three quintillion. This large number of possibilities makes solving Rubik’s cube more complicate. Thus we aimed to use this complexity in the proposed encryption algorithm, which can make more difficulty for hackers in obtaining the original message.
Rotation of Rubik’s cube (RRC): Rotation of classical 3 × 3 × 3 Rubik’s cube may be clock wise rotation or anti-clock wise rotation, it has different layers like upper (1), horizontal (2), down (3), upper-inverse (4), horizontal-inverse (5), downinverse (6), front (7), middle (8), back (9), front-inverse (10), middle-inverse (11), back-inverse (12), left (13), vertical (14), right (15), left-inverse (16), vertical-inverse (17) and rightinverse (18). On the whole, 18 different rotations are possible in 3 × 3 × 3 cubes.
Rotation Angle (RA): Rotation angle defines the angle of rotation of each layer, such as 90°, 180°, 270° and 360°. Rotation angle 360° remains same as the angle starts rotation, so the rotation of cubes layer can be carried out in three different angles 90°, 180° and 270°. Rotation angle 270° is remain same as anti-clock wise rotation angle of 90°, so we carried out either 270° of clock wise rotation or 90° of anticlock wise rotation. Rotation angle 180° is same for both clock wise and anti-clock wise rotation.
Proposed Methods
Cubical message
Original message is equally divided into 6 different blocks and number of cube (N) is formed by taking data from 6 blocks, number of pieces in each cube is made of BSize. Cubical message contain
BSize=(3 × 3)pieces × 6faces=54 → (2)
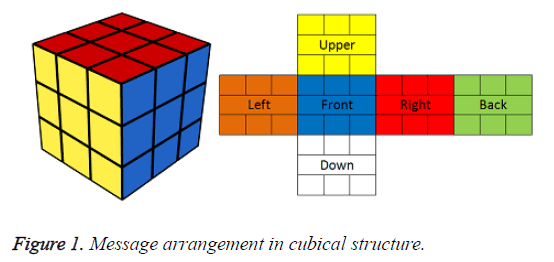
For 3 × 3 × 3 cube, message is divided into N number cubes each cube contains 54 pieces and each 54 pieces is formed into six different faces (3 × 3 of 6 matrices) containing nine pieces each. Each matrix are arranged in cubical space by six different faces front, back, upper, right, left and down as shown in Figure 1.
Rotation type and rotation angles
Cube’s rotation type is defined randomly by generating random sequence. Possible rotations are derived from that sequence, each value defines the type of rotation for the cube containing original message. For 3 × 3 × 3 Rubik’s cube, 18 different rotations types are possible. The cube containing original message will be undergone all the 18 different rotations by obtaining values from the randomly generated sequence. Rotation angle can be defined as three degrees of rotations such as 90˚, 180˚, and 270˚. It contains randomly generated values in the set {1, 2 and 3}, 1 defines the 90˚ rotation, 2 define the 180o rotation and 3 define the 270˚ rotation of cubical layers.
Proposed Algorithms
In this session, we propose the (i) key generation algorithm, (ii) encryption algorithm based on Artificial intelligence Rubik’s cube rotation using encryption (iii) decryption algorithm.
Key generation algorithm
Input: Number of rotation NR
Output: Random sequence of rotation types RT1UR and Random sequence of rotation angles RAR
Step 1. Generate the unrepeated random sequence for Rotation Type (RT1UR) of NR length defined in equation (1) for the rotation of cube. Element RT1UR [i] takes the random value from the set R = {1, 2, 3… NR}.
RT1UR [i] ϵ {1, 2, 3 … NR} where [1 ≤ i ≤ NR] → (3)
Step 2. Generate the random sequence for Rotation Angle (RAR) of length NR to ensure the angle of each rotation. Element RAR[i] takes the random value from the set C={1, 2 and 3}.
RAR[i] ϵ {1, 2 and 3} where [1 ≤ i ≤ NR] → (4)
Cube RT1UR and RAR are consider as secret keys in the proposed key generation algorithm. Based on the message length, the number of keys increases proportionally. Generated key is a symmetric key, it is used in both encryption and decryption algorithm. Key is more secure as it is generated through random function for the rotating cube.
Text scrambling encryption algorithm using rubik’s cube rotation
Input: Message M, RT1UR and RAR are the keys for encrypt the message
Output: Scrambled Message (SM)
Step 1. Partition the original message into equal number of 6 (cube faces-CF) blocks. Creating the 3 × 3 × 3 cubes by taking data from CF blocks for making CF different small matrices such as front (F), back (B), upper, (U), right (R), left (L) and down (D) with size (BSize/CF). Each number of pieces in the cube is made of BSize as mentioned in equation (2). Thus it generates Mlength/BSize number of message cubes (MC), where Mlength is the length of the message.
Step 2. Rotation of message cube (MC [i], where 1 ≤ i ≥ Mlength) is based on RT1UR and rotation angle is based on RAR value. MC [i] is i th message cube going to rotate. Rotation of MC [i] is based on consecutive values of RT1UR totally 18 different rotation along with rotation angle RAR Rotation angle of MC [i] is based on the values of RAR,
rotate (MC (c), RT1UR [i], RAR [i]) → (5)
Where [1 ≤ i ≤ NR] and [1≤ c ≤ Mlength]
Equation (5) rotation algorithm takes the input as message, rotation type and rotation angle. It produces the shuffled message using cubical message.
Step 3. Repeat the Step 2, until all cubes are encrypted with possible rotations.
Step 4. After all sides and angles of entire cubes all rotated, cube’s face values are printed one by one to get the unpredictable scrambled message (SM).
Decryption algorithm
Input: Scrambled Message (SM), RT1UR and RAR are the keys for decrypt the message
Output: Original message M
Step 1. The cipher text is partitioned in to N different block size (BSize). Each block’s value is arranged in CF different small matrices such as front (F), back (B), upper, (U), right (R), left (L) and down (D). The size of each face value BSize/CF is tending to form cubical structure that is cipher cube (CC).
Step 2. Rotate of cipher cube–CC [1 to Mlength] is based on RT1UR and rotation angle is decided based on RAR value. CC [c] is c th cipher cube to get scramble to get original message. Rotation of CC [c] is based on consecutive value of RT1UR from upper bound to lower bound Rotation is carried out in anti-clock wise instead of clock wise and vice-versa to compare with encryption algorithm. Rewriting the equation (3) that is,
RT1UR [i] ϵ {1, 2, 3, … NR} where i from [NR, NR-1 … 1] → (6)
Rotation angle of CC [c] is based on RAR, and value is taken from upper bound to lower bound.
deRotate (CC [c], RT1UR [i], RAR [i]) → (7)
Where, i is from NR to 1 that is [NR, NR-1 … 1] and [1 ≤ c ≤ Mlength]
Step 3. Repeated the step 2, until all sides and angles of every cube is decrypted using possible inverse rotations.
Step 4. After rotating entire cubes, all cube’s face values are rearranged and makes large cube with six face values. All six face values will be printed one by one to get the original message without any loss.
Experimental Results
Following is the experimental analysis implemented for 3 × 3 × 3 Rubik’s cubes
Scrambling of original message using 3 × 3 × 3 cube
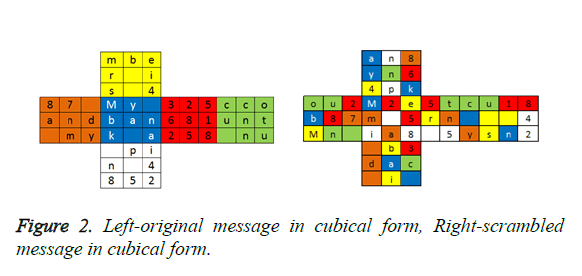
Consider the original message as “My bank account number-432568125887 and my pin as 4852” formed as cubical format in Left side of Figure 2 and each face value is differentiated by colors. After scrambling the original message, cipher text is shown as cubical form in right side of Figure 2.
After scrambling the message using the key as shown in Table 1, position difference between original and scrambled message is more than 94%. Scrambled cipher text is “m2em 5ia8u18 4sn2an8yn64pk5tcrn 5you2b87Mn b3dac i”
| Angle | 1 | 3 | 2 | 2 | 1 | 1 | 3 | 1 | 1 | 3 | 3 | 1 | 3 | 3 | 1 | 3 | 3 | 1 |
| Rotation Type | 16 | 2 | 17 | 10 | 7 | 9 | 5 | 12 | 14 | 1 | 18 | 11 | 3 | 6 | 13 | 4 | 8 | 15 |
Table 1. Key to scramble the original message.
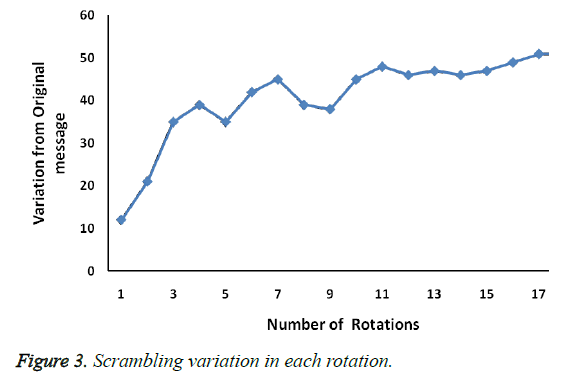
As the number of rotation increases the variation of the text in corresponds to the original message also increases. Scrambled as shown in Figure 3, message incrementally varies with original message for 3 × 3 × 3 cube.
Scrambling of original message with unique characters
Consider the original message “abcdefghijklmnopqrstuvwxyz ABCDEFGHIJKLMNOPQRSTUVWXYZ12”, which contains only unique characters without any repeated characters.
Using the key as shown in Table 2 the original message is scrambled and the scrambled message generated as per the proposed algorithm is “yhHzntpdaSE2veRjflJITPFYMUVgxikwo A1KrGcmXbDNZQWBCOquLs”
| Rotation Type | 1 | 9 | 12 | 8 | 4 | 2 | 16 | 11 | 7 | 15 | 18 | 3 | 6 | 17 | 10 | 14 | 13 | 5 |
| Angle | 2 | 1 | 3 | 1 | 3 | 1 | 1 | 3 | 3 | 2 | 3 | 2 | 3 | 1 | 3 | 1 | 2 | 2 |
Table 2. Key to scramble the original message.
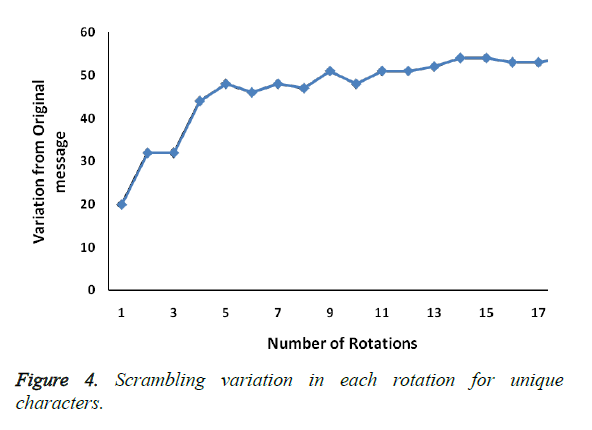
As the number of rotation increases the variation of the text in corresponds to the original message also increases. Figure 4 shows scrambled message is varies incrementally compare with original message with unique characters for 3 × 3 × 3 cube.
Position analysis between original message and cipher message with unique characters
Consider “abcdefghijklmnopqrstuvwxyz ABCDEFGHIJKLMNOPQRSTUVWXYZ12” as original message with unique characters to encrypt. Cube is rotated with the key as given in Table 3.
| Rotation Type | 8 | 6 | 3 | 7 | 17 | 16 | 1 | 15 | 18 | 5 | 2 | 12 | 14 | 13 | 11 | 4 | 9 | 10 |
| Angle | 1 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 1 | 1 | 3 | 1 | 1 | 1 | 1 | 3 | 3 |
Table 3. Key to scramble the original message.
After rotate the cube based on the given key pattern, obtained cipher text is “MbjmefZtrVv2CnWyYglP cxOUDzsJ1iRwkQGSahBNXIKdpuqHLFoAET”
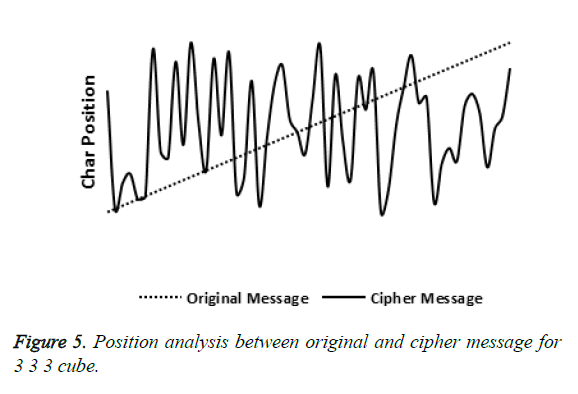
Normally almost all cipher text’s character’s position is distant from the postion of original text’s character’s position. Figure 5 shows the proposed algorithm’s result that ~90% of characther’s position is remote compared to their original position and it is evident that hackers will not find the original text’s character’s correct position without key.
Performance of key generated using random function number for 3 × 3 × 3 cube
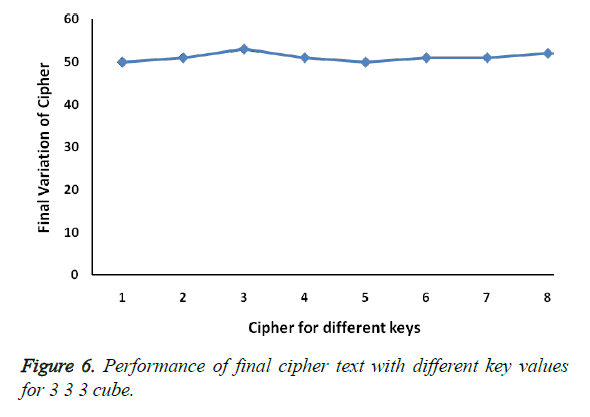
The text “My bank account number is 432568125887 and my pin 4852” is scrambled with different randomly generated key values and their equivalent cipher text generated after all the rotation of 3 × 3 × 3 cube is shown in Table 4.
| S. No | Final Scrambled Message | Final variation (Number of Characters) |
|---|---|---|
| 1 | i2yna dki 8na5s5mo rnuM1287ap be48c2 n t b34nu68m5cy | 50 |
| 2 | s42b 5ume5b n n4 mM6i18r273ct cn2 5 8nkpayau 8i8dnao y | 51 |
| 3 | mbu5n6 m 47ypaceas raun5iy881k4 i n 3 8n n2 cMbo28d5t2 | 53 |
| 4 | kbinaiay8M7u5nbems4rou84 2m yc p a2 5n 58n3 6ctn12d8 | 51 |
| 5 | M1k a4 82i b r25 ey 5n23ns5uydncamoin848n bump8ta7c6 | 50 |
| 6 | e58 82m72 26nd5boyy85ntaa ncb mMui31 c iunk8r4pa4 ns | 51 |
| 7 | in8c8ay5 268ynn4nM b 5n1 4cspet b5 mor3d u72aukmai 28 | 51 |
| 8 | 4 3bncy5m iita 8n257aa8n y cu m n pe2d86 582Mk4obn1urs | 52 |
Table 4. Final cipher text after rotation of cube with different keys for 3 × 3 × 3 cube.
To ensure the performance of the key pair generated by random number function, here eight different keys pairs are generated randomly for 3 × 3 × 3 cube to scramble the sample original text. At the end of scrambling the sample text using the eight different key pairs, the original text is scrambled more than ~90% shown in Figure 6. This shows that key pairs generated using the random number function is performing in a coherent manner.
Discussion
Key space strength
Strength of randomly generated keys RT1UR and RAR are highly secured to compare with ordinary sequential key spaces. Entire values in both sequences are randomly generated and it is hard to predict the sequence. Since 3 × 3 × 3 cube contains 18 different possible rotation types, so the possibility of rotation type is 18! (i.e 6.4023737e+15). Any one of the three different rotation angles is associated with all possible 18 rotation types. Hence the possibility of rotation angle is 318 (i.e 387420489). Total possible combinations are
18! × 38 = 2.4804108e + 24
Thus the key space is very hard to find and it is more secure and strengthened. Encryption algorithm strength is based on key size and hardness of the key space. More hardness in the key space ensures the strongest and high security of the encryption algorithm. Hence our encryption algorithm attests this high security by the key space.
Cipher text space strength
Each 3 × 3 × 3 cipher cube contains BSize values, which is acquired from 6 different blocks of original message. So the decryption of single cube is meaningless, the original message will be obtained only after the decryption of all cubes. Even single cube’s possibilities are
8! × 38 × (12! × 2) × 211 = 43.252003e + 18 × N
It is likely to unbearable for cryptanalysis like brute force attack or anagram. Cipher text in cubical form is more secure and much difficulty in breaking. Single rotation to the message gives the sufficing of original message in unpredictable sequence.
Analysis of cube rotation type and rotation angle
Scrambling of cubical text fully depends on key’s rotation type and angle of rotation. A 3 × 3 × 3 cube has 18 different possible rotation types, in which each type of rotation is more similar with other 3 rotations. For example, while performing upper rotation remaining down, horizontal and upper-inverse rotations are more similar. So it cannot produce best scrambling result when it will happen one after another. In this research similar rotation as well as same rotation type one after another is eliminated. In session earlier, it has been already mentioned that elimination of using 360° rotation angle is meaningful. We showed that, it improves the performance by using the rotation angle of 90° instead of 270°.
Conclusion
In summary, the proposed encryption algorithm uses rotation type and rotation angle of 3 × 3 × 3 cube, which is generated as a key using random number function to scramble the text in cubical form. The original text can be scrambled in an extensive manner because the scrambling of a text is done in the cubical format. The sample text scrambled in this paper has employed the key that is generated using random number function, and so it is not possible to predict the scrambling pattern by hackers. Compared with one dimensional and two dimensional scrambling methods, the proposed cubical space methods allow more complex scrambling. The experimental result shows that the proposed Artificial intelligence encryption algorithm generates unpredictable patterns. This Artificial intelligence scrambling techniques applied in web based data transfer will make the transaction more safe and secure. Even though the sequence of the original text is unpredictable by the hackers, scrambled content of the original text can be viewed by them. But the Artificial intelligence proposed algorithm combined with the cryptographic substitution, the above obstacle can be simply overcome.
References
- Iokibe K, Maeshima K, Watanabe T, Toyota Y. Security simulation against side-channel attacks on Advanced Encryption Standard circuits based on equivalent circuit model. 2015 IEEE International Symposium on Electromagnetic Compatibility (EMC), Dresden, 2015, 224-229.
- Patel H, Rusty OB. Random forest profiling attack on advanced encryption standard. Int J Appl Cryptography 2014; 3: 181-194.
- Obukhov DS, Chai Z. ENCRYPTION KEY SELECTION.Patentscope2015; WO/2015/183355.
- Shantharajah SP, Duraiswamy K, Nawaz GMK. Key Management and Distribution for Authenticating Group Communication. 1st International Conference on Industrial and Information Systems, Peradeniya, 2006, pp. 133-137.
- Gregory MZ, Brown DRL. Randomness for encryption operations. U.S. Patent Application No. 13/481,077 2012.
- Singla P, Sachdeva P, Ahmad M. A Chaotic Neural Network Based Cryptographic Pseudo-Random Sequence Design. 2014 Fourth International Conference on Advanced Computing & Communication Technologies, Rohtak, 2014, 301-306.
- KumarKM, AzamMS, Rasool S. Efficient Digital Encryption Algorithm Based On Matrix Scrambling Technique.Int J Network Security Appl2010.
- Adrian-Viorel D, Loukhaoukha K. An improved secure image encryption algorithm based on Rubik's cube principle and digital chaotic cipher. Math Problem Eng2013.
- Gomathi T, Shivakumar BL. Multistage Image Encryption using Rubik's Cube for Secured Image Transmission. Int J Adv Res ComputSci 2015; 6: 54-58.
- Rajavel D,Shantharajah SP. Cubical key generation and encryption algorithm based on hybrid cube's rotation. Pattern Recog Inform Med Eng2012.
- Zhang L, Tian X, Xia S. A Scrambling Algorithm of Image Encryption Based on Rubik's Cube Rotation and Logistic Sequence. International Conference on Multimedia and Signal Processing 2011;1: 312-315.