Research Article - Biomedical Research (2017) Volume 28, Issue 6
Optimization of a non-linear conical tank system using Cuckoo algorithm for Pharmaceutical industries
Marshiana D1* and Thirusakthimurugan P2
1Department of Electronic and Instrumentation, Sathyabama University, Chennai, India
2Department of Electronic and Instrumentation, Pondicherry Engineering College, Pondicherry, India
- *Corresponding Author:
- Marshiana D
Research Scholar, Department of Electronic and Instrumentation
Sathyabama University, India
Accepted date: November 15, 2016
Abstract
In this paper an evolutionary algorithm, which can be used for non-linear optimization problems, is introduced. The non-linear system taken up for the study is conical tank system because it is used in the field of medical sciences. Its non-linearity is due to the cross sectional behaviour of the process for the evacuation of products without wastage is possible. To control the level for the tank, the closed loop performances are determined with the conventional PI controllers. It is optimized by an Optimization algorithm which is motivated by the egg laying activities of bird cuckoo. The major advantage of this method is simplicity and used as a simple optimization algorithm. Application of the projected algorithm to some standard functions and a real problem has confirmed its capability to deal with difficult optimization problems. Simulation results show that the proposed the proportional integral controller outperforms with its optimization.
Keywords
Non-linear system, Cuckoo search optimization algorithm, Proportional integral controller, Performances indices.
Introduction
The level control in a process industry provides a major role in the industries. The raw material may include solvents, slurries, viscous and solids [1]. To pass up the rusting and maintain the flow of the process evenly can be done by using a conical tank system. Owing its shape in conical tank the raw resources can be disposed easily and quickly. It assures optimal rousing and addition of ingredients. It provides a fast and hygienic cleaning. The majority of the pollution happening occurs due to spillage, overcapacity of tanks, reduced practice and poor treatment facilities. In the highly industrialized countries, to improve the process safety and efficiently utilize resources can be made by controlling of level. In the developing countries, the main endeavour is the production of products should be fast for developing process automation [2]. The furthest requirement in the process automation is used in many industries like the petrochemical industry, chemical industry, Pharmaceutical industry and power generating engineering [3,4]. The significance of automation knowledge provides a tremendous to increase in the process industries. The control of level in tanks is an essential issue in process industries without providing wastage to the materials used. However the automation provides more difficulties due to the non-linearity behaviour of the conical tank system. The nonlinearity is due to the shape because the area of cross section is non-uniform. A controller can be designed for a nonlinear process but it is difficult and terribly hard to realize it. The principle assignment of the controller design is to accomplish the ideal working conditions and to design the controller to attain its most favourable execution performance.
A nonlinear process, whose process variable changes the parameters which is considered for conical tank level process. The desired set point level is maintained with a fixed and controlled outlet flow rate. The process gain and time constant are the important precipitate which varies as a function of level in the chosen process. The need to control a level for the reason that if the level becomes too high which may upset reaction equilibrium of the total process in which it may cause damage to apparatus, or cause in spillage of expensive or perilous material from the process [4]. If the level is too low, it may provide bad consequences for the chronological operation carried out by the process. Therefore, control of liquid level is an important responsibility in process industries. Non-linear model is used wherever accuracy in a wider range of operation is required where they can be directly incorporated into control techniques. The non-linear conical tank system which finds wide application in process industries [4]. The nonlinearity which is due to its change in shape [5-7] and their shape assures optimal stirring and mixing of ingredients and provides a fast and hygienic cleaning.
This paper aims to create a new algorithm for the non-linear conical tank, called Cuckoo Search, which depends on the breeding behaviour such as brood parasitism of cuckoos. Behaviour of Cuckoo depends on the characteristics of Levy distribution of levy flights and then formulate the new search and it its implementation.
Methodology
The mathematical modelling and the various controller techniques for the conical tank system are determined. Optimization methods like the cuckoo algorithm are to determine the proportional and integral value with the minimization of integral square error.
Cuckoo search optimization algorithm
Cuckoo optimization algorithm is developed depending on the brood parasitism of the bird name as the cuckoo has a habitat of laying eggs in the nest of other (host) birds. To avoid that the host birds discover their eggs, they remove the eggs laid by other birds and also increases the possibility of hatching their own eggs in the communal nests. In this host birds can slot in direct clash with the obtrusive cuckoos [8-10]. If the eggs of the cuckoo are identified by the host birds, they will throw the Martian eggs away or build new nest elsewhere. Some of the female cuckoos are very special in mimicry the pattern and color of the host eggs to which they lay their eggs. In this cuckoo brood parasitism can be classified as the different types first as intraspecific brood parasitism [10,11] next as mutual breeding, and the last as nest capturing. In general, the eggs of cuckoo will hatch a little earlier than other host eggs [12,13]. When the cuckoo chick is hatched, the first impulse deed will take is to eject the host eggs by blindly propel the other host eggs away from its home nest, that can increases the cuckoo chick’s which can gain food provided by its host bird.
Various study show that a cuckoos chick can also able to mimic the dub of host chicks to realize admittance to added food feeding prospect.
Levy flight
Levy flight is a method of using a haphazard walk probability distribution in which the step length is considered [14]. If the walk is defined in a space whose dimension is greater than one then their steps are designed using isotropic random directions. The distribution of step size (U) is based on function
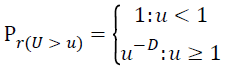
Where D is fractional dimension. Levy flight is a mixture of long trajectories and short, random movements. It is generally interspersed with the Brownian motion of the animals or birds but they are not so efficient when compared with the levy search. Its characteristics are based on the multi scale normal diffusive patterns. Such behaviour can be applied for the optimization and optical search which provides a better capability. Cuckoo search can be done by using three ideal rules [15-17].
The cuckoo will lay only one egg at a time, and chuck its egg in randomly chosen nest.
The best nests with high quality of eggs will carry over to the next generations.
The number of available host nests is fixed, and the egg laid by a cuckoo is discovered by the host bird with a probability pa (0,1).
In such cases, the host bird if it finds the alien egg it can either throw the egg away or remove the nest, and build a new nest. For simplicity, this last rule can be approximated by the fraction value of pa. The n nests are replaced by new nests (with new random solutions) for its maximization problem.
The fitness quality of a solution can simply be relative to the value of the objective function. Levy flights and random walk can be given by an equation.
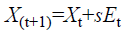
Where Et is the normal standard distribution with zero mean and standard unity deviation for random distribution or for levy flights using levy distribution. It is used to link the likeness between the eggs of the cuckoo and the host bird which is very difficult to implement. The iterations can be made fixed using he step size [18].
Cuckoo search data
No. of parameters to be optimized, N=2 (P, I Values)
No. of host nests (population), NP=10
Discovery rate of Alien eggs, Pa=0.25
No. of iteration=100
Distribution factor of 0.3 and 1.99
Mathematical modelling
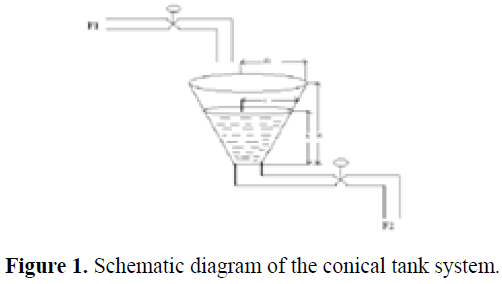
The mathematical model of the conical tank can be determined, by considering the assumptions (i) control variable (level) (ii) the manipulated variable (Tank inflow) [8]. This is accomplished by controlling inflow of the tank. The Figure 1 shows the schematic diagram of the conical tank system.
Operating parameters are
F1-Inflow rate of tank
F2-Outflow rate of tank
H-Total height of tank.
R-Tank top radius
h-Nominal tank level
r-Radius of nominal level of the tank
Mass balance Equation is given by
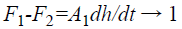
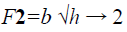
Where 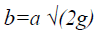
Where a-Outlet area of the tank
g-acceleration due to gravity
By substituting the Equation and considering the cross sectional area of the tank at level h
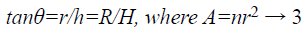
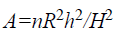
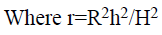
Transfer Function (TF) is given by taking the partial differentiation of the linearized equation and its corresponding Laplace transform [9].
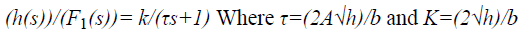
The experimental setup of the conical tank system is shown in Figure 2. Specification details of conical tank system are shown in Table 1.
| Reservoir tank capacity | 35 litres |
| Conical tank capacity | 22 litres |
| Conical tank height | 700 mm |
| Conical Tank Top diameter | 350mm |
| Conical Tank Bottom diameter | 25mm |
| Level transmitter type | Capacitive/Piezoelectric type |
| Measuring range | 700 mm |
Table 1: Specification details of conical tank system.
Based on the specification the transfer function is given by
G (S)=1.23/(313.198S+1)
Controller techniques
PI controller is a type of controller is incorporated because of the drawbacks of using the controllers P, I alone. Every controller is designed for the purpose of getting controlled output and to calculate the time domain performance such as rise time, settling time and performance indices like ISE (Integral Square Error), IAE (Integral Absolute Error) and ITAE (Integral Weighted Time Absolute Error) [19-24]. Feedback controller is used for the process whose output (control variable) depends on the set point, load and process variable. The error is calculated and can be minimized by optimizing the parameters [10,24-26]. The controller tuning parameters kp, ki, have to be adjusted so that the conical tank system is stable and gives the best performance.
Formulas for various controller tuning techniques and its values are shown in Table 2.
| Methods | Kp | τi | Kp | Ki |
| CC | 1/Km τm/d (9/10+d/(12τm )) | d((30+3 dm/τm)/(9+20 dm/τm)) | 117.06 | 10.471 |
| ZN | (0.9/Km)(τm/d) | d/0.3 | 114.857 | 7.3206 |
| CHR 0% | (0.6/Km) (τm/d) | 4d | 44.669 | 4.214 |
| CHR 20% | (0.7/Km) (τm/d) | 2.3d | 76.571 | 5.055 |
| CSA | - | - | 498.226 | 101.025 |
Table 2: Formulas for various controller tuning techniques and its values.
Ziegler Nichols method: The open loop response of the given transfer function is determined so as to calculate the tuning parameters. Ziegler Nichols tuning method is used to tune the parameters at an optimum level [27].
Cohen-Coon method: The Cohen-Coon method is said to be offline method for tuning of process it is because that the step change can be given to the input once it is at steady state. The output is calculated depending on the time constant, its time delay and its response can be evaluated to control the initial parameters [28].
CHR method: The Chien, Hrones, and Reswick (CHR) method of tuning was derived from the original Ziegler- Nichols Open loop method with the intention of obtaining the quickest response without overshoot and quickest response with 20% overshoot.
Experimental Results and Discussion
Simulation results are carried out for various controllers using Matlab software and it is compared with the Cuckoo optimization algorithm and implemented in the experimental setup.
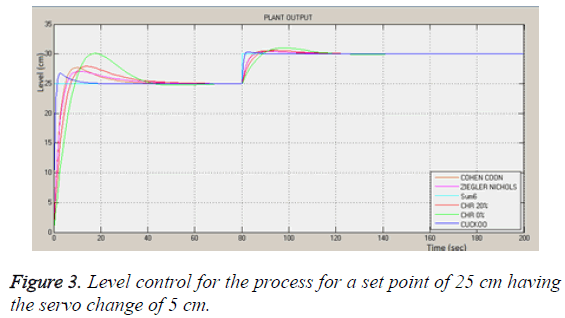
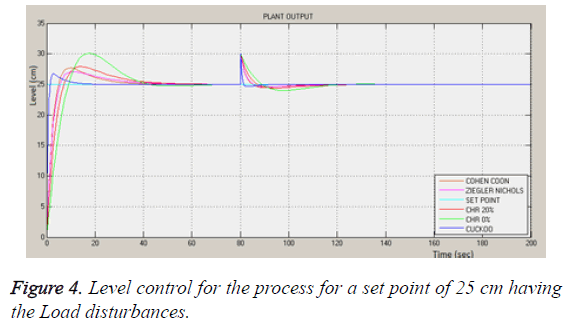
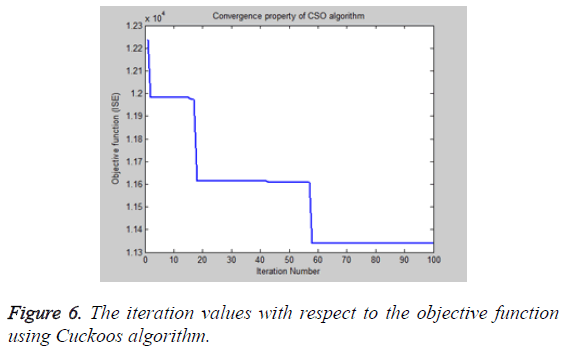
In Figures 3-6 the output obtained provides a steady state output for the various controllers for he given set point value for various controller techniques and optimization method based on Cuckoo algorithm. The values tabulated in Table 3 gives the various iterations carried out to find out the perfect values on optimization techniques. The load disturbance and the servo response provides a minimum settling time and reduces the error occurred due to the performances indices [29-31]. The Table 4 gives the performance of the various controller and optimization technique.
| Iteration | 5 | 16 | 35 | 43 | 58 | 84 | 100 |
| Kc | 487.7638 | 489.841 | 499.5849 | 499.7407 | 499.6765 | 499.6338 | 498.226 |
| Ki | 426.1302 | 345.8719 | 262.5692 | 263.3778 | 109.7389 | 110.7345 | 101.025 |
Table 3: Iteration values for PI controller using cuckoo algorithm.
| Methods | Rise Time | Settling Time | Overshoot | Peak | ITAE | IAE | ISE |
|---|---|---|---|---|---|---|---|
| CC | 8.0574 | 55.3424 | 10.8892 | 1.0896 | 657.2 | 81.83 | 657.2 |
| ZN | 8.9119 | 66.4839 | 8.5074 | 1.0851 | 912.8 | 86.63 | 388.2 |
| CHR 0% | 15.5432 | 76.9065 | 20.5013 | 1.2328 | 2337 | 186.6 | 175.1 |
| CHR 20% | 11.9743 | 78.2193 | 11.6245 | 1.0795 | 1386 | 122 | 162.9 |
| CSA | 2.2379 | 18.5454 | 6.9994 | 1.0700 | 60.18 | 20.96 | 158.8 |
Table 4: Controller performances of various controllers and optimization methods of cuckoo algorithm.
Conclusion
In this paper an optimized PI control output is determined based on the various iteration of the given transfer functions using CSO algorithm, the P and I values are determined. The comparison was made for various times domain specifications like rise time, settling time, overshoot and it is determined that CSA provides minimum settling time, minimum rise time and overshoot. The errors are reduced by performances indices like ITAE, IAE and ISE. The experimental results show that CSO algorithm provides better output when compared with other techniques. Thus cuckoo algorithm gives a better performance when compared with the other conventional controllers and it can apply to determine the PI controller values to provide better control of level in conical tank system.
References
- Ravi VR, Thyagarajan T.Application of adaptive control technique to interacting non -linear systems. Electronics Computer Technology (ICECT) 3rd International Conference 2011; 2: 368-392.
- Anandanatarajan RMC, Jayasingh T. Design of controller using variable transformations for a nonlinear process with dead time. ISA Trans2005; 44: 81-91.
- Nithya S. Design of Intelligent controllers for nonlinear processes. AJAPS 2008; 33-45.
- Nithya S. Soft computing based controllers Implementation for non-linear process in real time. Proc W Congr Eng Comp Sci2010; 2: 126-131.
- Marshiana D, Thirusakthimurugan P. Fractional order PI controller for nonlinear systems Control, Instrumentation, Communication and Computational Technologies (ICCICCT). Int Conf IEEE 2014: 322-326.
- Anandanatarajan R, Chidambaram M, Jayasingh T. Limitations of a PI controller for a first-order nonlinear process with dead time. ISA Trans2006; 45: 185-199.
- Davies NB, Brooke M, De L. An experimental study of co-evolution between the Cuckoo Cuculus canorus and its hosts. I Host egg discrimination. J Animal Ecol 1989; 207-224.
- Lotem A, Hiroshi N, Amotz Z. Rejection of cuckoo eggs in relation to host age: a possible evolutionary equilibrium. Behav Ecol1992; 3: 128-132.
- Gandomi AH, Xin SY, Amir HA. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng Comp2013; 29: 17-35.
- Rajabioun R. Cuckoo optimization algorithm. Appl Soft Comp 2011; 11: 5508-5518.
- Lotem A, Hiroshi N, Amotz Z. Constraints on egg discrimination and cuckoo-host co-evolution. Animal Behav1995; 49: 1185-1209.
- Dhivya M, Murugesan S. Cuckoo search for data gathering in wireless sensor networks. IntJ Mob Commun2011; 9: 642-656.
- Yang XS, Suash D. Multiobjective cuckoo search for design optimization. Comp Oper Res 2013; 40: 1616-1624.
- Tuba M, Milos S, Nadezda S. Modified cuckoo search algorithm for unconstrained optimization problems. Proceedings of the 5th European conference on European computing conference. World Sci Eng Acad Soc (WSEAS) 2011:263-268.
- Gandomi AH.2013 Design optimization of truss structures using cuckoo search algorithm. Struct Desig Tall Spec Build2011; 22: 1330-1349.
- Yang XS, Suash D. Cuckoo search via Levy flights Nature and Biologically Inspired Computing. World Congr IEEE 2009:210-214.
- Madhubala TK.Development and tuning of fuzzy controller for a conical level system. Intelligent Sensing and Information Processing. Proc Int Conf IEEE 2004:450-455.
- Aravind PMV, Ranganathan S. Modelling and simulation of non-linear tank. Int J Adv Res Electric Electr Instr Eng2013; 2: 842-849.
- Bhuvaneswari NS, Uma G,Rangaswamy TR. Neuro based model reference adaptive control of a conical tank level process. Cont Intel Sys2008; 36: 98.
- Visioli A. A new design for a PID plus feedforward controller. J Proc Contr2004; 14: 457-463.
- Pan H, Wong H, Kapila V, de Queiroz MS. Experimental validation of a nonlinear backstepping liquid level controller for a state coupled two tank system. Contr Eng Pract 2005; 13: 27-40.
- Murray-Smith DJ, Kocijan J, Gong M. A signal convolution method for estimation of controller parameter sensitivity functions for tuning of feedback control systems by an iterative process. Contr Eng Pract2003; 11: 1087-1094.
- Tan KK, Huang S, Ferdous R. Robust self-tuning PID controller for nonlinear systems. J Proc Contr 2002; 12: 753-761.
- Wu KL, Yu CC, Cheng YC. A two degree of freedom level control. J Proc Contr2001; 11: 311-319.
- Rojas I, Anguita M, Pomares H, Prieto A. 1997 analysis and electronic implementation of a fuzzy system for the control of a liquid tank. Proc IEEE Int Conf Fussy Sys 2001; 1541-1547.
- Aghaei A, Azadi S. Optimizing Azadi Controller with COA. Int J Comp Appl2013; 61: 8.
- Thangaraj R. Optimal gain tuning of PI speed controller in induction motor drives using particle swarm optimization. Log J IGPL 2010: 31.
- Francis BA, Murray WW. The internal model principle of control theory. Autom1976; 12: 457-465.
- Roy P. Level control of two tank system by fractional order integral state feedback controller tuned by PSO with experimental validation. 2016 IEEE First International Conference on Control, Measurement and Instrumentation (CMI). IEEE 2016.
- Kwok KE, Ping MC,Li P. Model-based augmented PID algorithm. J Proc Contr2000; 10: 9-18.
- Marshiana D, Thirusakthimurugan P. Design of deadbeat algorithm for a nonlinear conical tank system. Int Conf Rec Trends Comp2015; 1351-1358.
- Anand S, Aswin V, Rakesh KS. Simple tuned adaptive PI controller for conical tank process. Int Conf Rec Adv Electric Electr Contr Eng 2011; 263-267.
- Yang XS, Suash D. Cuckoo search via Lévy flights. Nat Biol Insp Comp 2009; 210-214.