Research Article - Biomedical Research (2017) Volume 28, Issue 9
Jaya-FLANN based adaptive filter for mixed noise suppression from ultrasound images
Manish Kumar* and Sudhansu Kumar Mishra
Department of Electrical and Electronics Engineering, Birla Institute Technology, Mesra, Ranchi, India
- *Corresponding Author:
- Manish Kumar
Department of Electrical and Electronics Engineering
Birla Institute Technology, India
Email: manish.guptasssss007@gmail.com
Accepted on February 15, 2017
Abstract
The noise which degrades the quality of Ultra Sound (US) images may not be of a unique type. Instead, it could be speckle noise inherent in US, impulse noise produced by switching circuits or Gaussian noise getting super-imposed during transmission. When noises of multiple origins and characteristics are present in the image, denoising becomes a difficult task because most of the existing filters are suitable for particular kind of noise. This paper presents a novel adaptive Jaya based functional link artificial neural network (Jaya-FLANN) filter for suppressing different noise present in ultrasound (US) images. Jaya is the optimization algorithm employed to assist in updating weights of FLANN. The target function for Jaya is the minimum error between noisy and contextual pixels of reference images. Compared to Wiener, Multi-Layer Perceptron (MLP), Cat Swarm Optimization based FLANN (CSOFLANN) and Particle Swarm Optimization based FLANN (PSO-FLANN), Jaya-FLANN filter is observed to be superior in terms of Peak Signal to Noise Ratio (PSNR), computational time.
Keywords
Adaptive filtering, Jaya algorithm, Neural network, FLANN, Optimization techniques.
Introduction
Ultrasound imaging is a non-invasive modality that has been extensively used for soft tissue imaging, especially in urology, gynecology, and obstetrics. US equipment is portable and inexpensive compared to other medical imaging techniques such as X-rays, Computed Tomography (CT), Magnetic Resonance Imaging (MRI), etc. More importantly, it is nonhazardous as ionizing radiations are not involved and produces good resolution real-time images. However, the images seem to be hazy and dominantly corrupted by the speckle noise. The speckle noise is a multiplicative kind of backscattered echoes and produces a random granular pattern in US images [1]. In addition to that, the acquired image may get affected by the Gaussian noise during transmission and by Impulse (Salt and Pepper) noise from switching circuits. Generally, Impulse and Gaussian noises produce grain and pimple like effects on images. It disturbs the clarity of the clinical images and hence the diagnosis. Denoising is a procedure, indispensable in automated or computerized US analysis. Software packages are available with the sonography equipment itself so that, the quality of images can be enhanced to make it ready for automated analysis. In general, denoising filters are of two categories which are non-adaptive and adaptive. Mean, median, weighted mean, weighted median and rank-order mean filter are some of the examples of non-adaptive filters. However, the non-adaptive filters suppress only a particular kind of noise, for which they are designed. For example, the median filter is suitable for salt and pepper noise. The mean filter is preferable for Gaussian noise. But, in real time, the noise which corrupts the image may not be of a particular type [2,3]. Hence, adaptive filters which perform well, irrespective of the type of noise and image are desirable. Adaptive filters tune their parameters according to the characteristics of the image and the statistics of noise in it [4]. Adaptive filters can be either linear or nonlinear. Wiener filter, Kalman filter, pseudo-inverse filter, etc. are examples of linear adaptive filters. They save computational time but suffer from generating blurred edges. Unlike linear filters, nonlinear adaptive filters remove noise without degrading the edge strength. Some of the nonlinear spatial filters are Anisotropic Diffusion (AD), Non-Local Means (NLM), Total Variance (TV), bilateral filter, etc. These filters have many arbitrary parameters which control their performance. Moreover, all of them are computationally complex and suitable for limited type of noises [5-9]. Neural network based realization of nonlinear filters is one of the recent approach for denoising [10]. The performance of Neural network based nonlinear adaptive filters is a well appreciated one on acoustic, images, Electrocardiography (ECG), Electroencephalogram (EEG), etc. [11,12]. Among the popular neural network models, Multilayer Perceptron (MLP) is the model widely used in adaptive filters [13]. However, the complexity of MLP is high because of the presence of multiple layers and consequently it has the lower rate of convergence. Radial Basis Function Based Neural Network (RBFNN) filter with limited number of hidden layers was reported to be suitable for X-ray and MRI images [14]. The implementation of multiple layers and Gaussian kernel made RBFNN also complex. FLANN which is a single layer neural network can resolve this issue. It circumvents the complexity of multilayer neural networks and confirms better result in less computational time [15]. The performance of neural network based filters greatly depends on learning scheme and hybridization. The training of the neural network can be based on derivative (gradient) or non-derivative algorithms. Derivative based techniques are Least Mean Square (LMS), Back Propagation (BP), Recursive Least Squares (RLS), etc. Error minimization is a one of the widely used objective function in most of the algorithm. The weights are updating in such a manner that the error is minimized. The process of updated weights in the neural network is otherwise called learning. Yaghini et al. [16] have listed the negative aspect of gradient-based learning algorithm as learning rate dependency, network sluggishness, and the possibility of trapping at the local maxima or minima of the optimal function. To overcome such problems, they demonstrated the benefits of derivative-free heuristic techniques. Derivative-free heuristic techniques include Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Cat Swarm Optimization (CSO), etc. Out of which, Dash et al. have employed GA for the training of FLANN filter [17]. Similarly, Pigeon-Inspired Optimization (PIO) [18] and Artificial Bee Colony (ABC) [19] are proposed for the training of neural filter. It can be noted that evolutionary methods have many arbitrarily defined parameters like crossover, mutation, inertia, population size, constriction factor, etc. in them. Selection of the arbitrary parameters in evolutionary algorithms itself is a crucial task. Sub-optimal selection of these parameters may affect the performance of the filter, and it may increase computational time significantly. Rao et al. [20-22] have recently introduced an optimization technique named as Jaya which does not require any algorithm specific parameters and utilized in various engineering application [23]. In this research paper, we extend our previous work [24-26] in which PSO and CSO based FLANN filter were implemented to remove noise from CT, MRI, and X-ray images. PSO and CSO depend upon inertia, cognitive and social parameters. Because of its dependency on the various parameters, these optimization techniques become more cumbersome and difficult to analyse. To avoid these shortcomings, a parameter free optimization approach named as Jaya is utilized to select the optimal set of weights of FLANN filter. Finally, this proposed Jaya based FLANN filter has been employed to eliminate mixed noise from US images. Jaya-FLANN filter is compared with other neural network filters based on LMS, PSO, and CSO. Rest of the paper proceed through the steps of Jaya-FLANN algorithm, selection of its parameters and its performance evaluation on US images.
Materials and Methods
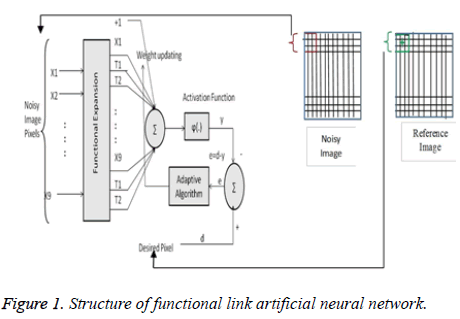
In the proposed Jaya-FLANN filter, nine pixels of noisy ultrasound image has been selected from each sliding window of 3 × 3 and expanded nonlinearly using Chebyshev polynomials. The architecture is demonstrated in pictorial form in Figure 1. The input nine pixels are expanded by the following recursive formula based on Chebyshev expansion.
 (1)
(1)
 (2)
(2)
The total selected pixel intensities from noisy image are represented in a single array as,
T=[T1, T2, …., T8, T9] → (3)
The random ten sets of weights are initialized, and each set is assigned with expanded noisy inputs. The output of the network is passing through an activation function ‘Ψ’. The middle pixel ‘d’ of the reference image of the corresponding window is compared with output ‘y’ to evaluate the error.
y (n)=Ψ × [T (n) × w (n)T] → (4)
e (n)=d (n)-y (n) → (5)
The same procedure is applied with other nine sets of weights and shifted the window to successive rows as well as columns. Whole, process is repeated for fixed number of iteration and in each iteration the previous and current error is compared. The two sets of weight which give the minimum and maximum error are stored. The updated sets of weight are found out as follow.
 (6)
(6)
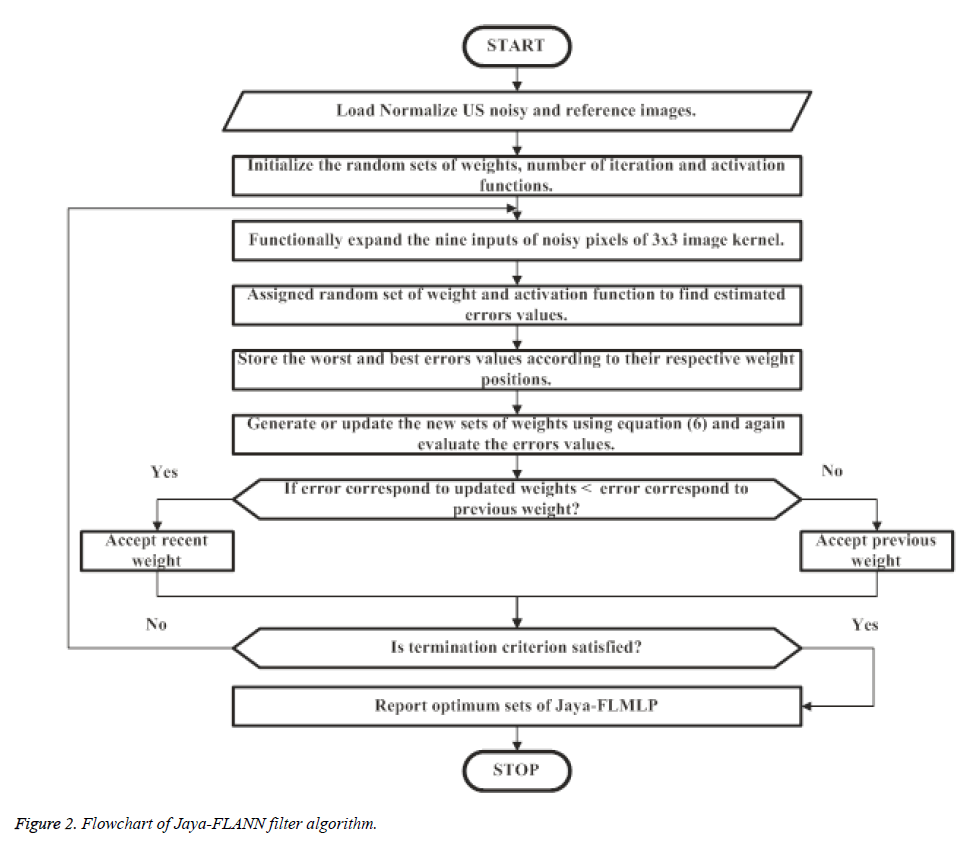
Where, w (n), wbest (n), and wworst (n) are the weight position, best weight position and worst position respectively. The proposed technique is summarized in the form of a flowchart in Figure 2.
Results
Original US images used in this paper are taken from Samsung Medison website [27]. All the experiments are performed in Matlab® on a personal computer with specifications Intel Core, i5 with 3.30 GHz speed, 8 Gb of RAM, 64-bit bus and
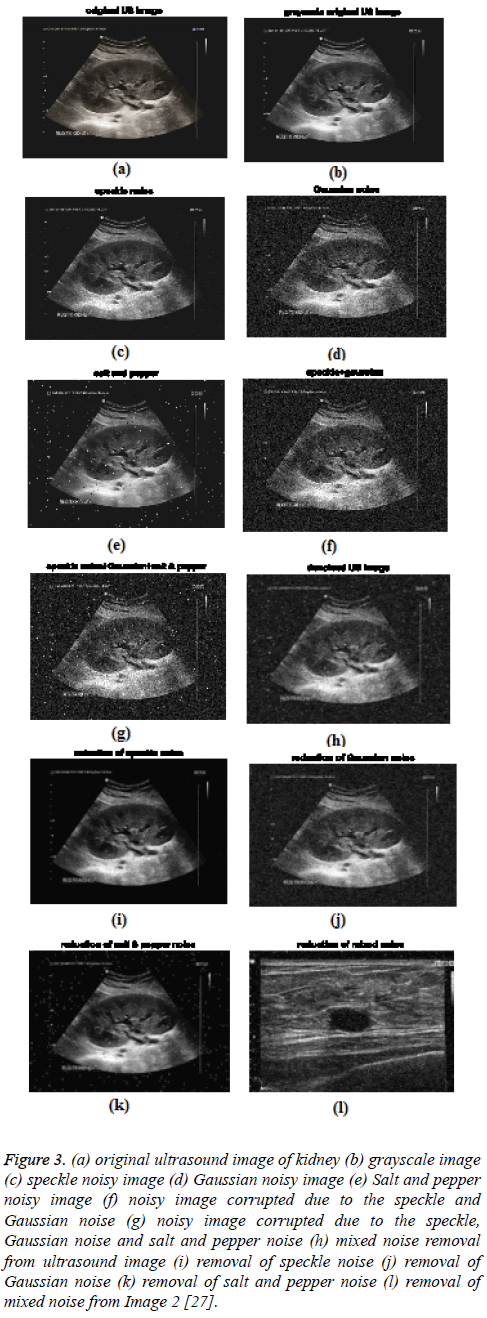
Windows 8 operating system. To validate our proposed algorithm in mixed noise condition in real world scenario, we synthetically introduced the speckle, Gaussian, and salt and pepper noises individually as well as in mixed form. The images used in this experiment are of JPEG format and 335 × 252 dimension. The noise free grayscale images are considered as the reference image. Reference (Figure 3b) and noisy images (Figure 3g) applied for the training purpose. Once the filter is trained, that can be utilized for any other new US image. Table 1 shows the values of different parameters of the network and algorithms. The density of speckle and impulse noises is taken as 0.02 and 0.01 respectively. Similarly, mean and variance of Gaussian noise is 0 and 0.01 respectively. The number of iteration is fixed at 1000 for all the networks. The aforementioned parameter values as shown in Table 1 are obtained from the final fine-tuned algorithms. The denoised images by Jaya-FLANN, given in Figures 3h to Figure 3l reveals that it is the filter can remove speckle, impulse,Gaussian noises and their mixture more efficiently as compared to others. The performance of the proposed Jaya- FLANN filter is compared with four neural network based filters such as BP-MLP, LMS-FLANN, CSO-FLANN and PSO-FLANN based on Peak Signal to Noise Ratio (PSNR). The performance result obtained from the proposed approach is also compared with that of Wiener filter. The formula for PSNR is mathematically expressed as
PSNR=10log10 (peak value2/MSE) → (7)
| Sl. No | ANN based | Parameters |
|---|---|---|
| Denoising methodologies | ||
| 1 | LMS-FLANN | Number of weights=(9 × 5)=45 |
| Learning rate=0.02 | ||
| Functional expansion=exponential(.) | ||
| Activation function=logsig(.) | ||
| 2 | CSO-FLANN [17] and PSO-FLANN [18] | Number of weights=(10 × 9 × 5)=450 |
| Functional expansion=exponential(.) | ||
| Activation function=logsig(.) | ||
| Inertia=mean((2/ no. of iteration)^0.3) | ||
| PSO acceleration constants C1, C2=2 | ||
| CSO acceleration constant=2 | ||
| 3 | JAYA-FLANN (Proposed) | Number of weights: (10 × 9 × 5)=450 |
| Functional expansion=Chebyshev(.) | ||
| Activation function: tanh(.) |
Table 1. Parameters employed in different ANNs filters.
Figure 3: (a) original ultrasound image of kidney (b) grayscale image (c) speckle noisy image (d) Gaussian noisy image (e) Salt and pepper noisy image (f) noisy image corrupted due to the speckle and Gaussian noise (g) noisy image corrupted due to the speckle, Gaussian noise and salt and pepper noise (h) mixed noise removal from ultrasound image (i) removal of speckle noise (j) removal of Gaussian noise (k) removal of salt and pepper noise (l) removal of mixed noise from Image 2 [27].
Mean square error
 (8)
(8)
Where, ‘M’, ‘N’ are the number of rows and columns in the image. ‘I’ is the reference and ‘K’ is the filtered image. The values of PSNR obtained from six different US images by applying all the six algorithms is demonstrated in Table 2.
| Images | Filters | Wiener | BP-MLP | LMS-FLANN | PSO-FLANN | CSO-FLANN | Jaya-FLANN |
|---|---|---|---|---|---|---|---|
| Noisy | |||||||
| Image 1 | 28.26 | 31.37 | 34.74 | 35.38 | 35.44 | 35.59 | 35.73 |
| Image 2 | 27.25 | 31.49 | 33.52 | 33.55 | 34.6 | 34.69 | 34.31 |
| Image 3 | 28.18 | 30.81 | 33. 26 | 34.43 | 35.31 | 35.67 | 35.88 |
| Image 4 | 29.12 | 32.98 | 33.19 | 33.26 | 33.93 | 33.62 | 33.54 |
| Image 5 | 27.43 | 31.68 | 32.85 | 33.89 | 35.27 | 35.48 | 35.21 |
| Image 6 | 26.97 | 30.12 | 31.33 | 31.22 | 31.59 | 32.46 | 32.66 |
Table 2. PSNRs (in dB) values of different filters.
| Algorithms | WIENER | BP-MLP | LMS-FLANN | PSO-FLANN | CSO-FLANN | Jaya-FLANN |
|---|---|---|---|---|---|---|
| Ranking | 3.5 | 6.83 | 9 | 11.83 | 12.83 | 13 |
Table 3. Average ranking of filtering algorithm on Friedman’s test.
| Source | Sum of square (SS) | Degree of freedom (df) | Mean square (MS) | Chi-square | Critical value (p) |
|---|---|---|---|---|---|
| Columns | 433 | 5 | 86.6 | 15.19 | 0.0096 |
| Error | 511 | 24 | 21.3 | ||
| Total | 969 | 35 |
Table 4. Friedman statistical parameters.
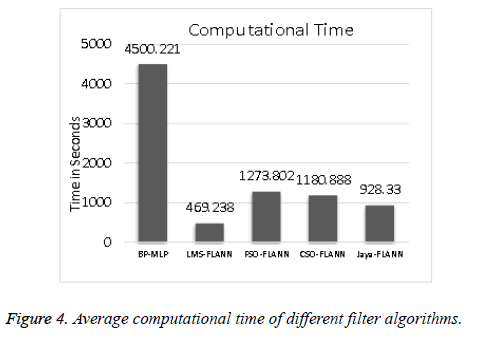
Table 2 reveals that in the case of Images 1, 3 and 6 Jaya- FLANN give superior performance as compared to others. Similarly, the CSO-FLANN has better performance in case of Images 2 and 5. The PSNR obtained from PSO-FLANN is maximum in Image 4. Hence, it can be concluded that the derivative free algorithms perform better in terms of PSNR value. The computational complexity of all the six algorithms is also investigated for analysing their performance. The computational time requirement is least in the case of LMS based FLANN network and highest in BP-MLP algorithm. Their average computational time is illustrated in Figure 4. It can be noticed that the derivative learning algorithm is superior in terms of computational time.
Discussion
The performance of BP-MLP, LMS-FLANN, CSO-FLANN and PSO-FLANN depends on various parameters at the time of learning the weights. However, the proposed Jaya-FLANN filter does not depend upon any parameters such as learning rate, inertia, acceleration constant, etc. In this paper, the Jaya- FLANN filter is introduced for suppressing noise from US images. In the simulation studies, it is evident that, in terms of the ability to remove mixed noise, in most of the cases Jaya- FLANN performs superior as compared to other filters. Moreover, the filters based on FLANN exhibit satisfactory results as compared to others because of its inherent nonlinearity present due to functional expansion. The performance of different algorithms is also analysed using a nonparametric statistical test i.e. Friedman’s test. The average rankings of the filters and Friedman statistical parameters are depicted in Tables 3 and 4 respectively. The inference obtained from the average ranking shows the superiority of Jaya- FLANN over others.
Conclusion
A novel Jaya based FLANN filter has been proposed and successfully applied for removing speckle, impulse, Gaussian and mixed noises from US image. Jaya-FLANN offers superior performance in terms of PSNR and computational time in most of the US images. The proposed filter is adaptive to image type and noise statistics. From the simulation studies, it is evident that the proposed Jaya-FLANN filter generate satisfactory results irrespective of types of noise and its density. The filtered US images obtained from Jaya-FLANN enhance the manual and automated diagnostic accuracy. The versatility of the proposed filter can also be tested on other modalities, such as MRI, CT, etc.
Appendix

References
- Babu JJ, Sudha GF. Adaptive speckle reduction in ultrasound images using fuzzy logic on coefficient of variation. Biomed Sign Proc Control 2016;23:93-103.
- Wang YQ, Morel JM. Can a single image denoising neural network handle all levels of gaussian noise? IEEE Sign ProcLett 2014;21:1150-1153.
- Jiang J, Zhang L, Yang J. Mixed noise removal by weighted encoding with sparse nonlocal regularization. IEEE Trans Image Proc2014;23:2651-2662.
- Toprak A, Ozerdem MS, Guler I. Suppression of impulse noise in MR images using artificial intelligent based neuro-fuzzy adaptive median filter. Dig Sign Proc 2008;18:391-405.
- Sondes T, Hassene S, Zouhair M, Ezzedine BB. RGB image de-noising using new low-pas filter with variable Gaussian core real time optimizedby neural networks. ElectrEng Software Appl (ICEESA) International Conference 2013;1-6.
- Zhang D, Mabu S, Hirasawa K. Noise reduction using genetic algorithm based PCNN method. Systems Man Cybernetics (SMC) 2010; 2627-2633.
- He L, Greenshields IR. A nonlocal maximum likelihood estimation method for Rician noise reduction in MR images. IEEE Trans Med Imag2009;28:165-172.
- Joseph J, Sivaraman J, Periyasamy R, Simi VR. Noise based computation of decay control parameter in nonlocal means filter for MRI restoration. JMed Imag Health Inform 2016;6:1027-1037.
- Joseph J, Sivaraman J, Periyasamy R, Simi VR. An edge preservation index for evaluating nonlinear spatial restoration in MR images. Curr Med Imag Rev 2016;12:1-8.
- Zhou YT, Chellappa R, Vaid A, Jenkins BK. Image restoration using a neural network. IEEE Trans Acoustics Speech Sig Proc 1988;36:1141-1151.
- Qin H, Yang SX. Adaptive neuro-fuzzy inference systems based approach to nonlinear noise cancellation for images. Fuzzy Sets Sys 2007;158:1036-1063.
- Jafarifarmand A, Badamchizadeh MA. Artifacts removal in EEG signal using a new neural network enhanced adaptive filter. Neurocomputing 2013;103:222-231.
- Sivakumar K, Desai UB. Image restoration using a multilayer perceptron with a multilevel sigmoidal function. IEEE Trans Sig Proc1993;41:2018-2022.
- Debakla M, Djemal K, Benyettou M. A novel approach for medical images noise reduction based RBF neural network filter. J Comp 2015;10:68-80.
- Pao Y. Adaptive pattern recognition and neural networks 1989.
- Yaghini M, Khoshraftar MM, Fallahi M. A hybrid algorithm for artificial neural network training. EngAppl Artificial Intell 2013;26:293-301.
- Dash PP, Patra D. Evolutionary neural network for noise cancellation in image data. Int J Comp Vis Robot 2011;2:206-217.
- Duan H, Wang X. Echo state networks with orthogonal pigeon-inspired optimization for image restoration. IEEE Trans Neural Networks Learn Sys 2015; 27: 2413-2425.
- Saadi S, Guessoum A, Bettayeb M. ABC optimized neural network model for image deblurring with its FPGA implementation.MicroprocMicrosys 2013;37:52-64.
- Rao RJ. A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int JIndustrEngComput 2016;7:19-34.
- Rao RV, More KC, Taler J, Ocłon P.Dimensional optimization of a micro-channel heat sink using Jaya algorithm. ApplThermEng 2016;103:572-582.
- Venkata RR, Waghmare GG. A new optimization algorithm for solving complex constrained design optimization problems. EngOptim 2016; 1-24.
- Suraj S, Sinha RK, Ghosh S. Jaya based ANFIS for monitoring of two class motor imagery task. IEEE Access 2016;3536: 1-10.
- Kumar M, Mishra SK, Sahu SS. Cat swarm optimization based functional link artificial neural network filter for Gaussian noise removal from computed tomography images. ApplComput Intel Soft Comp 2016; 2016: 1-16.
- Kumar M, Mishra SK. Particle swarm optimization-based functional link artificial neural network for medical image denoising. Comp Vis Robot 2015;105-111.
- Upadhyaya A, Sagar P, Kumar M, Mishra SK. Particle swarm optimization-functional link multilayer perceptron for Riciannoise suppression from MRI images. Global Trends Sig Proc Inform ComputCommun 2016;22-24.
- Ultrasound images. Available from: http://www.samsungmedison.com/ultrasound/gen eral-imaging.