Research Article - Biomedical Research (2017) Volume 28, Issue 6
Hagen-Poiseuille equation: A non-invasive tool for detecting renal pelvic pressure
Yansheng Li1, Yancheng Wang2, Xiuwu Han1, Xuhui Zhu1, Tao Li1, Peng Zhang1, Hui Shan1 and Xiaodong Zhang1*
1Department of Urology, Beijing Chaoyang Hospital Affiliated to Capital Medical University, Beijing, PR China
2Department of Urology, Xinghe County People's Hospital, Wulanchabu, PR China
- *Corresponding Author:
- Xiaodong Zhang
Department of Urology
Beijing Chaoyang Hospital Affiliated to Capital Medical
University, PR China
Accepted on November 24, 2016
Abstract
Flexible Ureteroscopy (F-URS) has become an effective modality for treatment of upper urinary tract stone. This study aims to assess the feasibility of using Hagen-Poiseuille equation as a tool for speculating Renal Pelvic Pressure (RPP) during F-URS. The ureteral access sheath and polyscope were placed in the upper urinary tract model in a standard fashion. A tube was placed in the renal pelvis transparenchymally for pressure measurement. A saline bag surrounded by the pressure cuff of a mercurial sphygmomanometer provided the irrigating fluid at a constant flow rate in the Polyscope under a given pressure. The 20 mmHg pressure gradient was set from 100 mmHg to 300 mmHg. After building the in vitro model, the pressure drop (ΔP) across Polyscope was measured (ΔPm), or was calculated according to the Hagen-Poiseuille Equation (ΔPc). The flow rate (Q) was calculated by perfused fluid volume divided by the perfusion time. The variable (l) was obtained by length measuring. The radius (R) was available in the published literature. The viscosity of water and saline was tested. Finally, the ΔPc and ΔPm was compared statistically. Results showed that, ΔPc from Hagen-Poiseuille Equation failed to fit perfectly with ΔPm, but the regression model showed there was a strong linear relationship (R2=0.977) between them. The linear regression equation was established as ΔPm=0.992 ΔPc-29.498. Hagen-Poiseuille equation can be hopeful as a non-invasive validated tool for predicting the RPP during F-URS.
Keywords
Flexible ureteroscopy, Hagen-Poiseuille equation, Renal pelvic pressure, Feasibility.
Introduction
Flexible Ureteroscopy (F-URS) has become an effective modality for treatment of upper urinary tract stone. Due to the miniature nature of the device, it is essential to have irrigating fluid for maintaining a good visualization. When irrigating fluid is forced into the relatively closed and confined renal pelvis, it’s prone to cause Renal Pelvic Pressure (RPP) elevated dramatically. A colloidal suspension of fine particles created by holmium lasertripsy combined with suspension of debris on stone fragmentation can result in poor visualization and a higher pressure will be needed [1]. It may soar further in case of bleeding in renal pelvis. The sharp rise of RPP can result in complications such as Systemic Inflammatory Response Syndrome (SIRS), damage to the kidney even urosepsis and so on.
Some efforts like access sheath and isoproterenol are utilized to reduce the RPP [2,3]. However, the access sheath can’t reach the renal pelvis all the time in clinical practice and efficiency of drainage will not be ideal. Obviously the drug is also not a definitive way. Therefore, it is better to monitor the RPP in real time. To date there is still not any reliable way for the RPP measurement due to the limitation of device and the anatomy of the upper urinary tract.
Hagen-Poiseuille equation may be able to play a role to infer RPP in real time. The law states the relationship between flow rate (Q) pressure drop across the tube (ΔP), the tube radius (R)and the tube length (l) (Equation-1),which has been used in medical science [4,5]. Herewith, we explored the feasibility of the alternative indirect way to achieve that goal.
Materials and Methods
Viscosity measurement
Fluid viscosity of water and saline was measured using a Fungilab-APM (Fungilab, Sant Feliu de Llobregat (Barcelona, Spain). Tests were carried out at a temperature of 0°C.
Measuring ΔPm
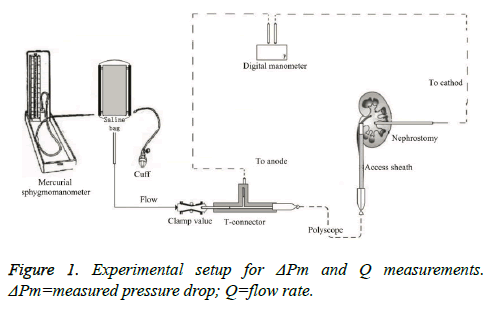
As shown in Figure 1, the unilateral upper urinary tract of domestic pig was obtained from the slaughterhouse.Nephrostomy was done through the middle calyx of the kidney, through which a tube was placed to connect with the cathode of TPI-655L digital manometer (Summit Inc., Seoul, Korea). Following the F12/14 Ureteral Access Sheath (Cook Medical Inc., IN, USA) placed through the ureter above ureteropelvic junction, the PolyScope (Poly Diagnost Gmb H, Pfaffenhofen, Germany) advanced to the renal pelvis level of the kidney in a standard fashion. Then the inlet end of the PolyScope was attached to anode of the pressure gauge through a T-connecter. The third way of T-connecter was connected to the saline bag via a short tube controlled by a clamp valve. The saline bag was surrounded by the pressure cuff of a mercurial sphygmomanometer (Yuyue Medical Equipment Inc., Nanjing, China). The pressure gauge and the kidney were placed in the same horizontal level. It was clear that reading of pressure measuring device indicated the real pressure drop (ΔPm) across PolyScope.
Calculating ΔPc
The umen of the system was filled with saline for system priming. After occluding the tube clamp valve, pressure on the saline bag was given by the mercurial sphygmomanometer. The pressure cuff embracing the saline bag was inflated to a given level (from 120 mmHg to 300 mmHg; 20 mmHg pressure gradient was adopted). After the pressure indicator resetting to zero, the tube clamp valve was released and timing was started by a stop watch simultaneously. The continuous inflating was applied to the saline bag by an assistant for maintaining the given pressure level. After 20-30 s, the clamp valve was shut down and timing was terminated at the same time. The residual saline volume in the bag was measured by a measuring cylinder. The perfused fluid volume in the period of time was equal to the original volume minus the residual volume. Further, the flow rate (Q) could be calculated by perfused fluid volume divided by the perfusion time.
The variable length (l=0.83 m) could be obtained by measuring the full length of PolyScope. The radius (R=0.6 mm) was available from manufacture or in the literature [6]. The viscosity coefficient (η) of saline from viscometer suggested it varied slightly with time and similar to that of water at temperature of 0°C, which suggested saline could be deemed to be a Newtonian fluid, and it’s viscosity coefficient could take that of water as a surrogate. The temperature of saline in this experiment was 21°C and viscosity coefficient could be 0.9810 × 10-3 [7].
After the flow rate (Q), the tube length (l) and fluid viscosity (η), the tube radius (R) were all available. The calculated pressure drop across the tube (ΔPc) could be worked out according to the Equation 1: ΔPc=(8 ηlQ)/(πR4).
Statistical analysis
Data are presented as mean ± SD. The normal distribution of the data was confirmed via Shapiro-Wilk test before statistical analysis (P>0.05). Linear regression was established to compare the calculated pressure drop (ΔPc) (independent variables) with the measured pressure drop (ΔPm) (dependent variables) across PolyScope. The Pearson’s coefficient of determination (R2) and the model equation were provided. P<0.05 was considered as statistically significant. All statistical tests were performed using SPSS 22.0 statistical software (SPSS Inc., Chicago, IL, USA).
Results
Viscosity measurement
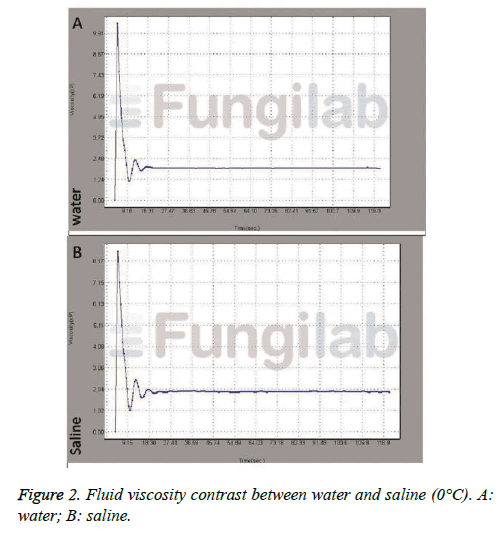
Due to the accuracy of Fungilab-APM with adapter for low viscosity was limited to 1-2 Cp, we compared the viscosity of both at 0°C (the viscosity of water at 0°C was 1.7921 Cp4). Theoretically a fluid with a constant viscosity at a certain fluid velocity could be called a Newtonian fluid. Figure 2 indicated that the viscosity of saline was a fixed constant at a given temperature, which was approximately the same as that of water at the same temperature (both approximate to 1.9 cP) and they both could be deemed to be a Newtonian fluid. It was proved that the saline could apply to the equation.
ΔPm and ΔPc at different SBP
Table 1 showed the 10 repetition data (mean ± SD). From 120 mmHg to 300 mmHg of SBP, 20 mmHg pressure gradients were adopted. At any SBP level, ΔPm and ΔPc were obtained. At the level of 300 mmHg and 275 mmHg, there were outliers we rejected, which was obvious ridiculous. There was a clear tendency of overestimating the ΔPm.
| ? | SBP | N | Mean | SD |
|---|---|---|---|---|
| ΔPm | 300 | 9 | 238.8889 | 4.37163 |
| 275 | 9 | 213.3333 | 2.29129 | |
| 250 | 10 | 195.8 | 6.95701 | |
| 225 | 10 | 183.2 | 3.93841 | |
| 200 | 10 | 162.1 | 4.38305 | |
| 175 | 10 | 139.8 | 2.78089 | |
| 150 | 10 | 117.9 | 4.09471 | |
| 125 | 10 | 100.2 | 3.96653 | |
| 100 | 10 | 79.8 | 2.78089 | |
| ΔPc | 300 | 9 | 265.7872 | 9.55886 |
| 275 | 9 | 244.9437 | 10.63372 | |
| 250 | 10 | 224.7405 | 5.9541 | |
| 225 | 10 | 214.5982 | 4.818 | |
| 200 | 10 | 194.502 | 8.53644 | |
| 175 | 10 | 175.9074 | 9.26634 | |
| 150 | 10 | 150.0401 | 7.23734 | |
| 125 | 10 | 127.4406 | 6.17411 | |
| 100 | 10 | 111.5035 | 9.05637 |
ΔPm=measured pressure; ΔPc=calculated pressure; SBP=Saline Bag Pressure.
Table 1. ΔPm and ΔPc at different SBP.
Results of linear regression analysis
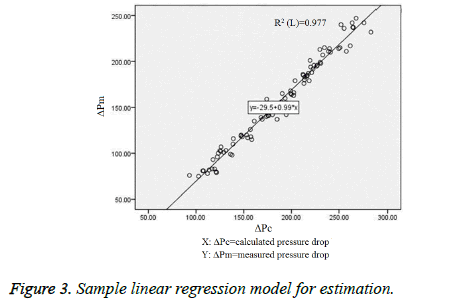
Because Newtonian fluid existed only in ideal condition, no real fluid fit the definition perfectly in fact. Saline could be assumed to be Newtonian for practical calculations under ordinary conditions. The ΔPc from Hagen-Poiseuille equation failed to fit perfectly with ΔPm. Fortunately, the regression model showed there was a strong linear relationship (R2=0.977) between two parameters. Figure 3 showed the regression model obtained to predict pressure drop (ΔP) from calculated pressure drop (ΔPc). The Equation ΔP=0.992 ΔPc-29.498 was established. The Pearson’s coefficient of determination (R2) was 0.977.
Discussion
Since the public reporting of the first flexible ureteroscopy in 1964 [8], it has played an increasingly important role in the treatment for upper urinary tract stone with the advancements of science and technology and the accumulation of clinical experience. For renal stones>20 mm, European Association of Urology Guidelines has recommended Percutaneous Nephrolithotomy (PCNL) as the first line modality. However, there are more and more literatures advocating it can be treated with flexible ureteroscopy [9-11]. Flexible ureteroscopy is also an alternative modality for diagnosis and treatment for upper urinary tract urothelial carcinoma [12].
Following the extension of indication for F-URS, chances for the RPP-related complication are more and more increasing. The elevated RPP above 40 cmH2O can cause fluid backflow around pelvis tissue [13]. The excessive pressure can result in infectious complications related to bacterial migration and renal extravasation, even irreversible damage on the kidney parenchyma [14]. Therefore, it is very meaningful for monitoring the RPP level intraoperatively in order to provide basis for clinical decision-making to reduce the risk.
Unfortunately there is still no ideal direct way to monitor RPP to date. Jung and associates retrogradely placed ureteral catheter in the renal pelvis for RPP measurements [15]. Although it is an effective way, the catheter is prone to interfere with the operation and to hinder drainage of irrigating fluid in renal pelvisboth of which contribute to RPP rise and prolonged operation duration. While measurement can be performed through nephrostom, it is both invasive and of the loss-outweight-gain for regular patients, and it can only apply to patients with nephrostomy access prior to F-URS [16].
Fortunately there seems to be a non-invasive indirect way to achieve that goal. When fluid flows through a long cylindrical thin tube, there is a pressure drop produced between two ends. That’s why hydrostatic pressure law doesn’t work and we can’t use Perfusion Pressure (PP) as a surrogate for the RPP arbitrarily. In this condition Hagen-Poiseuille law may allow us use PP to infer the RPP.
Hagen-Poiseuille equation, also known as the Hagen-Poiseuille law has been widely used in medical science [4,5]. Singh et al. used Hagen-Poiseuille law to offer some rationale for perfusing equipment selection in organ preservation [17]. The law states the flow rate (Q) is related to the pressure drop across the tube (ΔP), the tube radius (R) and the tube length (l) (Equation 2:Q=(πR4ΔP)/8 ηl) [17], or we can rewrite the equation in another way (Equation 1).
As shown in the reedited Poiseuille's equation (Equation 1), the pressure drop (ΔP) across the tube is proportional to flow rate (Q), the tube length (l) and fluid viscosity (η), while is inversely proportional to the tube radius (R) to the fourth power. If the equation does work in flexible ureteroscopy and we can determine the variables on the right side of the equation in vitro, the pressure drop (ΔP) on the left can be calculated. Further the RPP during flexible ureteroscopy will be work out following the PP measurement (Equation 3: RPP=PP-ΔP). To explore the availability of Poiseuille's equation during flexible ureteroscopy, we carried out our experiment.
We took PolyScope as the object of our study for several reasons. Firstly, it is making up of multiple individual modular including the outer catheter, the optic bundle connected to the camera system and so forth [6]. It is a semi-disposable flexible ureteroscope, which means the outer catheter part is for singleuse and can be utilized in our experiment. The advantages of convenience and economy made it as our material. Secondly, all components can be assembled as an entity mimicking the regular ureteroscope. In other words, it can be seen as the disassembled version of regular ureteroscope. The conclusion from PolyScope can also generalize to regular ureteroscope with similar working channel for perfusion. Our study took the outer catheter as materials, leaving the other study-unrelated parts aside. The outer catheter of 8F (2.65 mm) contains a working channel of 3.5F (1.2 mm), which is sufficient for our study [6].
The experiment simulated the actual flexible ureteroscopy to the uttermost. Access sheath and PolyScope were placed in the pig renal pelvis in a standard fashion. Just as the hand-operated pump, a given pressure was maintained on the saline bag to keep a constant flow rate. According to Hagen-Poiseuille equation, the fixed pressure determines the fixed flow rate (Q), allowing us to calculate the flow rate (Q) with the formula of volume divided by time. The anode and the cathode of the pressure measuring device were connected to the inlet end of the PolyScope and to the renal pelvis respectively. The reading indicated the actual pressure difference (ΔPm) between two ends precisely.
In our experiment, the hand-operated pump was chosen and simulated by pressure bag for some reasons. Firstly, a constant flow rate is the basis for Hagen-Poiseuille equation. Unlike the motorized pumps producing a pulse flow, both way above were able to maintain a constant flow rate which was more suitable for Hagen-Poiseuille equation. Secondly, since the perfusion volume for flexible ureteroscopy is not so much as for PCNL, hand-operated pump can be sufficient for demanding in clinical practice. The manually-operated devices may provide better visualization [18]. Thirdly, the advantages of dynamic control of flow and pressure in real-time have made it a popular choice nationwide in our country.
Theoretically only Newtonian fluid can apply to the equation. A fluid with a constant viscosity at a certain fluid velocity can be called a Newtonian fluid [16]. That is to say the viscosity coefficient of Newtonian fluid is a fixed constant at a given temperature. In another words, all the fluids that can be deemed to be Newtonian fluid have the same viscosity. As the common sense in the field of fluid mechanics, water can be seen as Newtonian fluid. For saline is a solution of water and salt, the small amount of sodium chloride in water can’t change the viscosity of water theoretically. To prove it, we tested the viscosity of water and saline. For the accuracy of Fungilab- APM with adapter for low viscosity was limited to 1-2 Cp and the viscosity of water at 21°C (0.981 Cp)4 was out of range, we compared the viscosity of both at 0°C (the viscosity of water at 0°C is 1.7921 Cp4) [7]. The results demonstrated the saline viscosity was a constant and the same as that of water and could be deemed to be Newtonian fluid (Figure 2). The saline we used in experiment was 21°C under room temperature and the viscosity (η) could be 0.9810 × 10-3 Pa • s [7]. Tube length (l=0.83 m) could be obtained via length measurement and tube radius (R=0.6 mm) could be obtained from literature or manufacture. Based on the Hagen-Poiseuille Equation, we could calculate the ΔPc. Using statistic; we could explore the relationship between the actual press (ΔPm) and the calculated pressure (ΔPc).
The main finding of our experiment was that ΔPc from Hagen- Poiseuille Equation failed fit perfectly with ΔPm. There was a clear tendency of overestimating the ΔPm. Why is that? For Newtonian fluid exists only in ideal condition, no real fluid fits the definition perfectly in fact. Water and saline can be assumed to be Newtonian for practical calculations under ordinary conditions. So the “failure” can be partly explained. Fortunately the regression model showed there was a strong linear relationship (R2=0.977) between two parameters mentioned above. The linear regression equation was established (Equation 4: ΔP=0.992 ΔPc - 29.498).
The Hagen-Poiseuille Equation can apply to real F-URS in the same way as experiment did. In clinical practice, all the variables in the equation except pressure difference (ΔP) can be obtained in vitro. Based on Hagen-Poiseuille Equation, we can work out the pressure drop (ΔPc) across flexible ureteroscope. Likewise, the PP can be measured though Tconnector near the inlet ends of F-URS. We can get the RPP by the formula using simple subtraction (Equation 3).
There are some points worth noting in our study. Firstly, our experiment put pressure measurement device and renal pelvis in the same horizontal position, avoiding the influence of gravity on the pressure. It’s better to follow the same principle during flexible urteroscopy. Or we can offset the effect with hydrostatic pressure equation (p=ρ gh). Secondly, as mentioned above, irrigation systems like motorized pumps producing irregular flow rates may not be suitable for the Hagen- Poiseuille Equation and the regression model we built. Thirdly, theoretically the result of the experiment is not only limited to PolyScope and also suitable for various ureteroscope with similar circular working channel.
Our study has a number of limitations. The results come for in vitro model, so it is likely to be more complicated in vivo.Further investigation in vivo should be performed for verification. But it does not seem to affect the clinical implications of this experiment. This experiment is not the pursuit of accurate prediction of the RPP. Just as estimating Glomerular Filtration Rate (GFR) with formula (GFR=186 x (creat/88.4)-1.154 × (age)-0.203 × (0.742 if female) × (1.210 if black), it aims to estimate the approximate value of RPP, which provides doctor a certain basis for the clinical decision. For the inner diameter of T-Connecter is not the same as that of PolyScope, it may contribute to the failure of fitting with true pressure drop.
In conclusion, although Hagen-Poiseuille Equation is used widely in medical science, it is calculation results those can’t fit perfectly with true value during flexible ureteroscopy. But the linear tendency allows us use ΔP=0.992 ΔPc-29.498 as the validated tool to establish the bridge between them. Further base on the Equation 3 and the PP, Hagen-Poiseuille Equation can be a non-invasive validated tool to predict the RPP during flexible ureteroscopy.
References
- Ng YH, Somani BK, Dennison A, Kata SG, Nabi G, Brown S. Irrigant flow and intrarenal pressure during flexible ureteroscopy: The effect of different access sheaths,working channel instruments, and hydrostatic pressure. J Endourol 2010; 24: 1915-1920.
- Auge BK, Pietrow PK, Lallas CD, Raj GV, Santa-Cruz RW, Preminger GM. Ureteral access sheath provides protection against elevated renal pressures during routine flexible ureteroscopic stone manipulation. J Endourol 2004; 18: 33-36.
- Jung HU, Jakobsen JS, Mortensen J, Osther PJ, Djurhuus JC. Irrigation with isoproterenol diminishes increases in pelvic pressure without side-effects during ureterorenoscopy: A randomized controlled study in a porcine model. Scand J Urol Nephrol 2008; 42: 7-11.
- Turner MJ. Is pressure decrease at peak hyperemia attributed to Poiseuille or Bernoulli or both? Hypertension 2011; 58: e21.
- Reddick AD, Ronald J, Morrison WG. Intravenous fluid resuscitation: was Poiseuille right? Emerg Med J 2011; 28: 201-202.
- Ding J, Xu D, Cao Q, Huang T, Zhu Y, Huang K, Chen Y, Liang C, Qi J, Huang Y. Comparing the efficacy of a multimodular flexible ureteroscope with its conventional counterpart in the management of renal stones. Urology 2015; 86: 224-229.
- Liu GQ, Ma LX. Physical property data handbook for chemistry and chemical engineering. Beijing: Chem Indust Pr 2002; 14.
- Marshall VF. Fiber optics in urology. J Urol 1964; 91: 110-114.
- Cohen J, Cohen S, Grasso M. Ureteropyeloscopic treatment of large, complex intrarenal and proximal ureteral calculi. BJU Int 2013; 111: E127-131.
- Takazawa R, Kitayama S, Tsujii T. Successful outcome of flexible ureteroscopy with holmium laser lithotripsy for renal stones 2 cm or greater. Int J Urol 2012; 19: 264-267.
- Hyams ES, Munver R, Bird VG, Uberoi J, Shah O. Flexible ureterorenoscopy and holmium laser lithotripsy for the management of renal stone burdens that measure 2 to 3 m: a multi-institutional experience. J Endourol 2010; 24: 1583-1588.
- Leow JJ, Orsola A, Chang SL, Bellmunt J. A contemporary review of management and prognostic factors of uppertract urothelial carcinoma. Cancer Treat Rev 2015; 41: 310-319.
- Rehman J, Monga M, Landman J, Lee DI, Felfela T, Conradie MC, Srinivas R, Sundaram CP, Clayman RV. Characterization of intrapelvic pressure during ureteropyeloscopy with ureteral access sheaths. Urology 2003; 61: 713-718.
- Schwalb DM, Eshghi M, Davidian M, Franco I. Morphological and physiological changes in the urinary tract associated with ureteral dilation and ureteropyeloscopy: an experimental study. J Urol 1993; 149: 1576-1585.
- Jung H, Norby B, Frimodt-Moller PC, Osther PJ. Endoluminal isoproterenol irrigation decreases RPP during flexible ureterorenoscopy: a clinical randomized, controlled study. Eur Urol 2008; 54: 1404-1413.
- Shao Y, Shen ZJ, Zhu YY, Sun XW, Lu J. Fluid-electrolyte and renal pelvic pressure changes during ureteroscopic lithotripsy. Minim Invasive Ther Allied Technol 2012; 21: 302-306.
- Singh S, Randle LV, Callaghan PT, Watson CJ, Callaghan CJ. Beyond poiseuille: preservation fluid flow in an experimental model. J Transplant 2013; 2013: 605326.
- Tarplin S, Byrne M, Farrell N, Monga M, Sivalingam S. Endoscopic valves and irrigation devices for flexible ureteroscopy: is there a difference? J Endourol 2015; 29: 983-992.