- Biomedical Research (2012) Volume 23, Issue 4

Determination of measurement noise, conductivity errors and electrode mislocalization effects to somatosensory dipole localization

¹Atilim University Computer Engineering Department, 06836, Ankara, Turkey

²Hacettepe University Electrical and Electronics Engineering Department 06800, Ankara, Turkey

^*Corresponding Author:

G. Sengül
Atilim University
Computer Engineering Department
06836, Ankara, Turkey

Accepted Date: August 09 2012

Abstract

Calculating the spatial locations, directions and magnitudes of electrically active sources of human brain by using the measured scalp potentials is known as source localization. An accurate source localization method requires not only EEG data but also the 3-D positions and number of measurement electrodes, the numerical head model of the patient/subject and the conductivities of the layers used in the head model. In this study we computationally determined the effect of noise, conductivity errors and electrode mislocalizations for electrical sources located in somatosensory cortex. We first randomly selected 1000 electric sources in somatosensory cortex, and for these sources we simulated the surface potentials by using average conductivities given in the literature and 3-D positions of the electrodes. We then added random noise to measurements and by using noisy data; we tried to calculate the positions of the dipoles by using different electrode positions or different conductivity values. The estimated electrical sources and original ones are compared and by this way the effect of measurement noise, electrode mislocalizations and conductivity errors to somatosensory dipole localization is investigated. We conclude that for an accurate somatosensory source localization method, we need noiseless measurements, accurate conductivity values of scalp and skull layers and the accurate knowledge of 3-D positions of measurement sensors.

Keywords

EEG, source localization, somatosensory cortex.

Introduction

Electroencephalography (EEG) measures the scalp electrical potentials produced by electrical activities of the human brain due to body functions. The electrical activity of the human brain is commonly modeled by electrical dipoles. If the electrical activities of the brain (i.e. electrical dipoles) are known, then the scalp electrical potentials (EEG) can be calculated. But in reality the electrical activities can not be exactly known; besides, only scalp potentials can be measured. Calculating the spatial locations, directions and magnitudes of electrically active sources of human brain by using the measured scalp potentials is known as bioelectromagnetic inverse problem, electrical source imaging or more commonly source localization which is a multidisciplinary research field that is used to understand electrophysiological, hemodynamic, metabolic, and neurochemical processes that underline normal and abnormal brain functions [1-3].

Source localization is commonly used in medicine, especially in cognitive neuroscience, neurology, psychiatry, and psychopharmacology. In cognitive neuroscience, the event related potentials and temporal change of information processing mechanisms are analyzed. In neurology source localization studies are focused on localization of activities in somatosensory and motor cortex. Source localization finds most of its application in clinical neurology, especially dealing with the calculation of epileptic sources in epilepsy patients. Depending on the epileptic sources, an epileptic surgery may be planned [4-7]. In clinical applications source localization methods are commonly used in diagnosis and treatment of epilepsy, schizophrenia, depression, Parkinson and Alzheimer. Source localization is also used in Brain-Computer Interface (BCI) developments [8-9]. Source localization can be performed to identify regions of brains related to functional experiments. For example, the electrically active regions of the brain can be determined when a visual, auditory or somatosensory (touch, pressure, temperature, pain) stimulus is applied [10]. By this way the relationship between the applied stimulus and the electrical activities of the brain can be related. In this study we will focus on the cases where a somatosensory stimulus is applied. Somatosensory stimulus cause electrical activity on the somatosensory cortex, which lies posterior to the central sulcus, on the top of the brain.

An accurate source localization method requires not only EEG data but also the 3-D positions and number of measurement electrodes, the numerical head model of the patient/ subject and the conductivities of the layers used in the head model [2]. Source localization algorithms in the first stage assume a known source model and calculate the potential distribution at electrode positions (the so-called forward problem solutions); then compares calculated potential distributions and measured ones. Depending on the error between calculated and measured scalp potentials, the solution is changed to minimize the difference iteratively. The source configuration that gives the smallest difference between the calculated and measured potential in a given constraint is obtained by terminating the procedure [2].

In the early studies on source localization, the human head is assumed to be a sphere and spherical head models were commonly used. But it is known that spherical head model assumptions introduce errors [1,3]. With the development of high-resolution magnetic resonance and computerized tomography imaging system, realistic head models obtained from the MRI or CT images of the subject/ patient are used in source localization studies [11-12]. For the electrode positions; there are five different methods suggested to measure the electrode positions in 3-D: manual methods [13-14], RF digitizer usage [15-16], MRI-assisted methods [17-20], ultrasonic methods [21-22], and methods those use photogrammetric principle [23-25]. The review of these methods is given in the literature and is not repeated here [25]. Another data set that is necessary for accurate source localization is the conductivity/ resistivity of the tissues/compartments used in the head model, since they vary according to the age and health conditions of the subjects/patients [26-28]. So it is necessary to perform subject-specific conductivity estimation with a low error rate, and then use it for source localization. There are many studies trying to estimate the conductivities of the head layers [such as the ones 29-33], but it is out of the scope of this paper and they will not be repeated here.

The scope of this study is to calculate the effect of electrode mislocalization, measurement noise and conductivity errors to source localizations performed for the sources located in the somatosensory cortex. The organization of the paper is as follows: in the remaining part of the introduction section the simulation studies that investigate the effect of noise, electrode localization errors and conductivity errors to source localization performed all over the brain is summarized. In materials and methods section, the simulation studies performed are summarized, and then results are presented.

The influence of electrode misplacement and measurement noise to source localization has been investigated previously. Khosla et. al. performed simulation and human studies using a 4-layered spherical head model [15]. The locations of the dipoles are selected randomly all over the brain. In the simulations the scalp potentials were assumed to be measured by 31 electrodes. During the inverse problem solution all electrodes were assumed to be randomly displaced from their original positions and it is found that electrode mislocalization of about 50 mm causes about 5 mm dipole location and 5⁰ dipole orientation errors and they concluded that for the spherical head models electrode mislocalizations with standard deviations in the range of 2-50 mm introduce errors on the same order as those due to additive noise levels of 10% [15]. In a second study performed in spherical head model Van Hoey et. al. [34] used 27 electrodes and three-layered spherical head model. In forward simulations the electrode positions were changed by a random azimuth and elevation angle deviation from the standard positions. The angle deviations were set to be independent and identically distributed Gaussian numbers. During the inverse localization procedure standard electrode positions were assumed and electrode mislocalizations were not taken into account. As a result it is found that 7.8 mm source localization error is obtained for an average of 10 mm electrode positioning error. They also investigated the effect of measurement noise to source localization and they found that the effect of measurement noise can be reduced by averaging the data sets, but averaging does not influence the localization results in the case of electrode mislocalizations. So they strongly recommended that for accurate source localization it is necessary to determine the measurement electrode positions with less error. They concluded that it is important to reduce the measurement noise and the electrode localization error, as the influence of the latter is not reduced by taking into account multiple time instants [34].

There are a few studies dealing with the electrode localization errors in realistic head models. In the first one Wang et. al. [35] investigated the effect of measurement noise and electrode localization error to source localization. For the noisy measurement case they found that 8-10 dB measurement noise causes an average of 5 mm source localization error, and an average of 5 mm electrode localization error causes 4.98 mm source localization error, and it has the same effect of 8-10 dB measurement noise. When measurement noise and electrode localization errors are present at the same time, the source localization error increases to 7 mm [35]. In a second study Whittingstall et. al. used a source model consists of symmetric two dipoles and 64 EEG electrodes. In that study it is found that electrode localization error in the range of 0-1 cm causes a mean localization error of 6 mm without measurement noise. In realistic clinical conditions (added measurement noise with a SNR of 6 -12), the mean localization error due to electrode misplacement is approximately 3.3 mm greater than those caused by random noise [36].

Another important parameter that effects the source localization performance is the conductivities of the layers within the head model. In source localization applications the average conductivity values given in the literature is used or subject-specific conductivity estimation is performed. The effect of conductivity errors to source localization is also investigated by simulation studies. Pohlmeier et. al. used a realistic head model to investigate the effect of skull conductivity variances. In this study the average conductivity value of the skull given in the literature is used in forward simulations, but on the inverse solution the conductivity of the skull is varied and the source localization error due to this conductivity change is calculated. It is found that the 20% error of skull conductivity causes a source localization error of 3 mm [37]. Awada et. al., used a realistic head model obtained from MR images of a real subject in simulations and changed the conductivities between the upper and lower limits given in the literature. In that study it is found that conductivity deviations cause a source localization error of 5- 20 mm [38]. In another study Vanrumste et. al. investigated the effect of brain to skull conductivity ratio by simulation studies. In forward simulations brain to skull conductivity ratio is chosen to be 16, but on the source localization this ratio is chosen to be 80 and source localization error is calculated. It is found that source localization error due to brain to skull conductivity ratio error is 34 mm when 27 electrodes are used and it is 28 mm for 53 electrodes [39].

All the simulation studies mentioned so far [15,34-39] dealing with the effect of measurement noise, conductivity errors and electrode mislocalizations to source localization were performed for the electrical sources spreading all over the brain. There is no study dealing with the source localization approaches and the effect of the parameters for the special part of the brain, i.e. somatosensory cortex, motor cortex, or visual cortex. This simulation study focuses on the effect of noise, conductivity error and electrode mislocalizations to somatosensory dipole reconstructions in order to complete this lack.

Materials and Methods

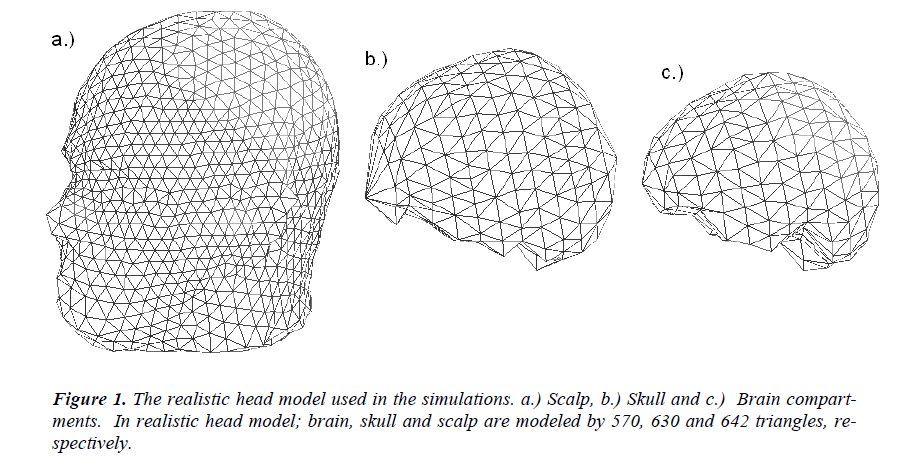
In this study a three-layer (scalp, skull and brain) realistically shaped head model obtained from high-resolution MRI images (1 mm thick slices using T1 weighted sequence in a 1.5 T system) of a patient is used as the head model. The realistic head model generation is performed by the segmentation the images. The surface potentials are calculated by boundary element method (BEM), and source localization is performed by a dipole fit algorithm. In the realistic head model obtained from the MR images of the patient, the brain, skull and scalp are modeled by 570, 630 and 642 triangles, respectively. The realistic head model used in simulations is given in Figure-1. 32 EEG electrodes (namely F5a, F1a, Fza, F2a, F6a, F5, F3, F1, F2, F4, F6, F6p, F4p, F2p, Fzp, F1p, F3p, F5p, T3, C5, C3, C1, Cz, C2, C4, C6, T4, T5a, P3a, Pz, P4a and T6a) placed according to the international 10-20 system are used as the measurement sensors.

Figure 1: The realistic head model used in the simulations. a.) Scalp, b.) Skull and c.) Brain compartments. In realistic head model; brain, skull and scalp are modeled by 570, 630 and 642 triangles, respectively.

Selection of dipoles on the somatosensory cortex

The EEG measurements performed during a stimulus is known as evoked potentials. If the stimulus is related to touch, then an electrical activity occurs in the somatosensory cortex. The EEG measurements performed during a somatosensory activity is known as the Somatosensory Evoked Potentials. The somatosensory cortex is located behind the central sulcus, on the top of the brain and it is responsible for processing of information related to touch. Using the nasion-ear reference system, the somatosensory cortex is assumed to be between -20 mm to 20 mm in x axis. For the realistic head model used in this study, it is found that the y axis is between y_min=-64.31 mm to y_max=70.52 mm. It is also found that for the brain region, the maximum point of z axis is z_max=115.2 mm.

The x axis components of the dipoles are selected by generating a Gaussian distribution with zero mean and 20.0 mm standard deviation. Similarly the y axis components of the dipoles are selected by using a Gaussian distribution with zero mean and 60.0 mm standard deviation. The dipoles whose x and y components are chosen outside the somatosensory cortex are ignored and new ones are selected. It is also assumed that the somatosensory cortex lies maximum 20 mm deeper from the cortex surface. The corners of the triangles used in brain modeling are found and then they are used for the calculation of z axis components of the dipoles.

For the dipoles whose x and y axes are determined previously, the z axis components are calculated by the following steps:

Step-1: For the dipole i, (whose x_i and y_i components are previously selected), the x_i and y_i components are compared with the corners of the triangles used in the realistic model and differences are calculated. Step-2: The corners of the triangle which is found to be nearest to x_i and y_i in step -1 are chosen to be Z_max. Step-3: Z_max is assumed to be brain surface for the dipole i (whose x_i and y_i components are previously selected). Then z_i component is selected by using a Gaussian distribution with a mean value of Z_max-10 mm., and a standard deviation of 10.0 mm, as well.

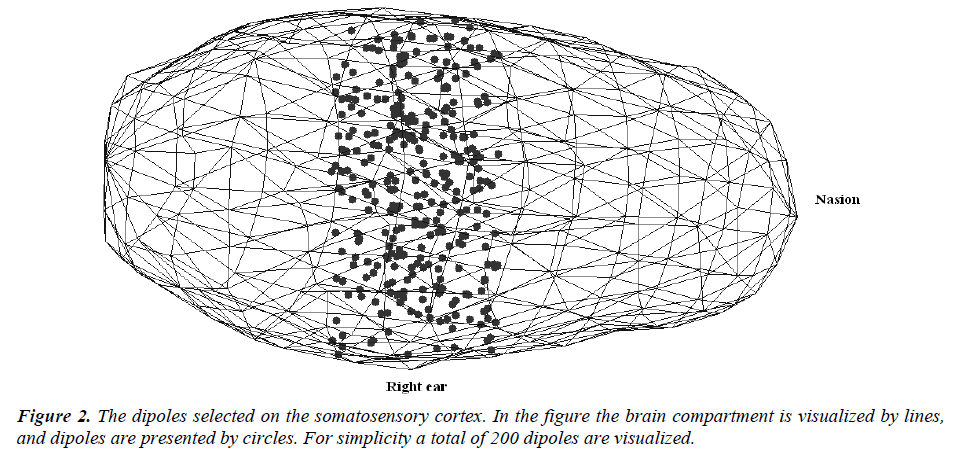
Step-4: All the components of the dipoles (i.e. dipole locations) are checked as if they are inside the brain. If not, then the dipole is ignored and a new one is selected. By using the steps described above, 1000 dipoles located in the somatosensory cortex are selected for the simulations. The dipole orientations are arbitrarily selected, and their magnitudes are set 1 (unit dipoles). The selected dipoles on the somatosensory cortex are presented in Figure -2. For simplicity a total of 200 dipoles are visualized. The dipole orientations are selected to be perpendicular to the brain surface, and ignored in visualization.

Figure 2: The dipoles selected on the somatosensory cortex. In the figure the brain compartment is visualized by lines, and dipoles are presented by circles. For simplicity a total of 200 dipoles are visualized.

In order to investigate the effect of noise, electrode mislocalizations and conductivity errors to somatosensory source localization, we performed three different simulations. In the first one, we investigated only the effect of measurement noise to somatosensory source localization. In this simulation, the conductivities of the layers are set to 0.33 S/m, 0.0042 S/m and 0.33 S/m, for scalp, skull and brain regions, respectively. These are the average conductivity values given in the literature. In the first simulation, we assumed that there are no conductivity errors and electrode positions are known exactly. For each test dipole generated as described above, the potential distributions at each electrode position is calculated by means of the forward problem solution. To simulate measurement noise a zero-mean Gaussian noise was added to simulated potentials. The strength of noise was adjusted to achieve 6 different signal-to-noise ratios (SNR), as in the study of Wang et. al. The selected SNR (defined as the square root of the signal power to noise power ratio) values are 4, 6, 8, 10, 12 and ∞. By using the noisy measurement for the test dipole, exact electrode locations and conductivities of the layers, a dipole fit algorithm (inverse solution) was applied and a dipole is estimated. The estimated dipole positions and orientations were compared with the original test dipoles and the position errors and orientation errors were calculated. Assuming the original position of the i-th dipole is x_i,o, y_i,o, z_i,o , and its estimated position is x_i,e, y_i,e, z_i,e , the average dipole position estimation error is calculated by Equation 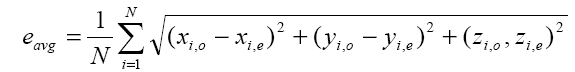1:

(1)

Where N is the number of test dipoles, and N=1000 in this study.

In the second part we investigated the effect of electrode mislocalization to somatosensory source reconstructions. We added random displacements to electrode positions. The electrode displacements were set to the range of 0-10 mm with a mean of 5.0 mm. By using the mislocalized electrode positions and noisy data the inverse source localization procedure were performed for different noise levels. The resultant dipole parameters were compared with the original ones and the localization and orientation errors were calculated according to Equation-1. In these simulations it is again assumed that layer conductivities are exactly known and thus have no effect source localization performance.

In the third part we investigated the effect of wrong conductivity estimations to somatosensory source localization. Because of this during the forward simulations we used the conductivity values of 0.33, 0.0042 and 0.33 S/m for scalp, skull and brain regions; respectively and during the inverse solutions we changed the conductivities of each region one by one. The conductivities of each region were changed by a ratio of 1%, 5%, 10%, 20% and 50%. The procedures were repeated for 1000 SEP dipoles and again the resultant dipole parameters were compared with the original ones and the mean localization and orientation errors were calculated. In the third case we assumed that the electrode locations are exactly known, and there is no measurement noise in EEG data.

Results

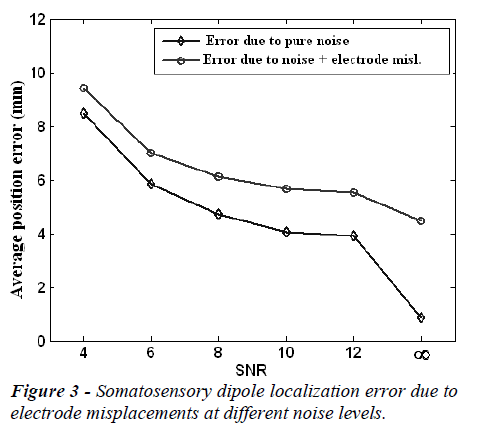
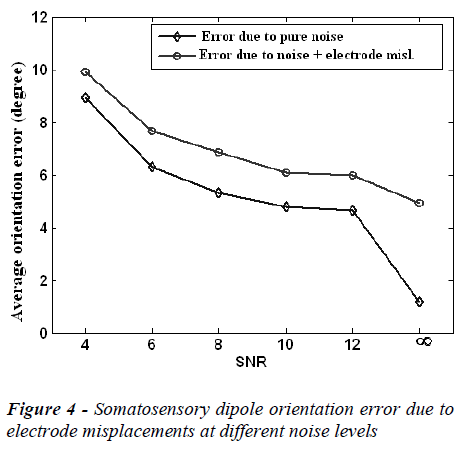
The mean localization position and orientation errors caused by electrode misplacements at different noise (SNR) levels are given in Figure 3 and Figure 4, respectively. In these figures the error without electrode misplacement (error due to pure noise) and the error caused by noise and electrode misplacements together are presented.

Figure 3: Somatosensory dipole localization error due to electrode misplacements at different noise levels.

Figure 4: Somatosensory dipole orientation error due to electrode misplacements at different noise levels

In the Figures 3 and 4, it is clear that the localization position and orientation errors for somatosensory dipoles are large at low SNR values and low at high SNR values, as expected. On the other hand when there is no measurement noise (SNR=∞) the localization position error is 4.03 mm and localization orientation error is 1.80 degrees for electrode mislocalizations. In real life situations the measurements are always noisy and in this case when the SNR is 6-10, the electrode misplacements also introduce about an extra 2 mm localization error to the source reconstruction procedure.

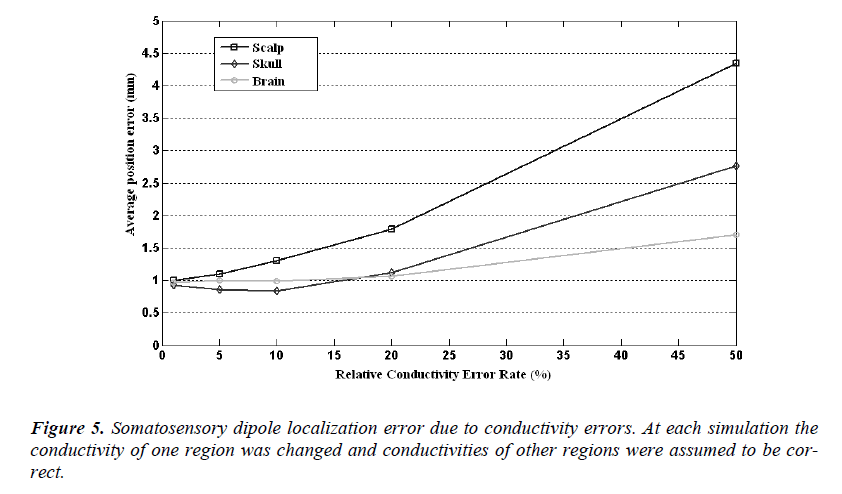
The source localization and orientation errors caused by the wrong conductivity assumptions are given in Figure 5 and Figure 6, respectively. In these calculations the conductivity of one compartment was changed at each step and the others were assumed to be identical to ones used in forward simulations. In Figure 5, it is seen that the localization error caused by a 1% conductivity error causes an error rate of 1 mm and the mean error increases as the conductivity error rate increases, as expected. For 50% conductivity error of skull and scalp, the meansource localization error is higher than 4 mm and 2.5 mm, respectively. But on the other hand 50% conductivity error of brain causes 1.6 mm somatosensory source localization error.

Figure 5: Somatosensory dipole localization error due to conductivity errors. At each simulation the conductivity of one region was changed and conductivities of other regions were assumed to be correct.

Figure 6: Dipole orientation error due to conductivity errors. At each simulation the conductivity of one region was changed and conductivities of other regions were assumed to be correct.

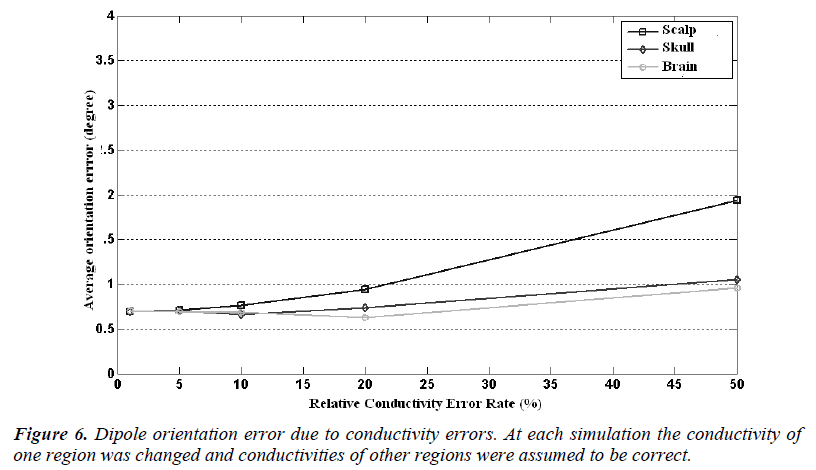
In Figure 5 it is seen that the dipole orientation error is minimum for 1% conductivity error and maximum for 50% conductivity error for each region. For a conductivity error range of 1% to 10%, the mean orientation error is between 0.7 degree to 0.8 degree and it is quite small and can be ignorable.

Discussion

In this study we investigated the effect of measurement noise, conductivity error and electrode misplacement to source localization of somatosensory evoked potentials. We showed that the effect of the measurement noise, conductivity errors and electrode misplacement can not be negligible and must be taken into account when working with somatosensory evoked potentials. In real life conditions the EEG measurements are subject to noise, and in this case a SNR value of 6 to 10 can be obtained. In this SNR values the localization error due to pure noise is approximately 5 mm. On the other hand when there are electrode shifts and noise at the same time, the localization error is about 6.5 mm.

The measurement noise is assumed to be a white-noise with Gaussian distribution. It is known that white noise can be reduced by averaging [35]. By averaging, the measurement noise can be reduced, so the SNR can be increased, causing less measurement noise. In this case when SNR is high, it is more important to know the accurate positions of the measurement electrodes. So it is important to precisely measure the measurement sensor positions in 3-D. A review of EEG electrode position determination systems can be found in literature [24-25]. As suggested at those works, the EEG electrode positions can be determined by the usage of photogrammetric systems, or MRI based systems with low error rates.

It is found in this study that tissue conductivities are another important parameter for somatosensory dipole localization. A scalp conductivity error rate of 50% introduces a mean somatosensory dipole localization error of 4.5 mm. On the other hand, skull conductivity error rate of 50% introduces a mean somatosensory dipole localization error of 2.8 mm. Brain conductivity error rate of 50% introduces lower source localization position error, on the order of 1.5 mm. This can be explained as follows: somatosensory dipoles are located on the top of the brain, just under the cortex, and there is a small volume of brain between those dipoles and measurement electrodes. Due to this positional constraint, the conductivity error of small volume of brain introduces less error of source localization. This is a new outcome about the source localization.

There are some simulations studies (as presented in the introduction section) dealing with the effect of electrode mislocalization, conductivity error and measurement noise to source localization for dipoles spreading all over the brain. On contrary this study focuses on the dipoles located just only on the somatosensory cortex. It is not meaningful to compare the results of this study with the previous ones, because simulation parameters such as the electrode number, forward and inverse solution algorithm, or head models differ. So it is better to asses the results of each study alone.

Conclusion

We conclude that for an accurate somatosensory source localization method, we need noiseless measurements, accurate conductivity values of the tissues and the accurate knowledge of 3-D positions of measurement sensors. Measurement noise can be reduced by averaging of multiple instants, and sensor positions can be determined by the studies suggested in [24], or [25]. For conductivity values, it is necessary to apply a subject-specific conductivity estimation procedure to estimate scalp and skull conductivities, as suggested in [29]. For brain, average conductivities given in the literature may be used.

References

1. Baillet S, Mosher J C and Leahy RM. Electromagnetic brain mapping. IEEE Signal Processing Magazine 2001; 18: 14-30.
2. Grech R, Cassar T, Muscat J, Camilleri KP, Fabri SG, Zervakis M, Xanthopoulos P, Sakkalis V, Vanrumste B. Review on solving the inverse problem in EEG source analysis. J Neuroeng Rehabil. 2008; 7: 5-25.
3. Michel CM, Murray MM, Lantz G, Gonzalez S, Spinelli L, Grave de Peralta R, EEG source imaging, Clinical Neurophysiology 2004; 115: 2195-2222.
4. Ebersole JS, Ebersole SM. Combining MEG and EEG Source Modeling in Epilepsy Evaluations. Journal Of Clinical Neurophysiology 2010; 27: 360-371.
5. Koessler L, Benar C, Maillard L, Badier JM, Vignal JP, Bartolomei F, Chauvel P, Gavaret M. Source localization of ictal epileptic activity investigated by high resolution EEG and validated by SEEG. Neuroimage 2010; 51(2): 642-53.
6. Plummer C, Harvey AS, and Cook M. EEG source localization in focal epilepsy: Where are we now? Epilepsia. 2008; 49(2): 201-18
7. Zijlmans M, Huiskamp G, Hersevoort M. EEG-fMRI in the preoperative work-up for epilepsy surgery. Brain 2007; 130(9): 2343-2353.
8. Nicolas-Alonso LF, Gomez-Gil J. Brain Computer Interfaces, a Review. Sensors 2012; 12(2): 1211-1279.
9. Krusienski DJ, Grosse-Wentrup M, Galan F, Coyle D, Miller KJ, Forney E, Anderson CW, Critical issues in state-of-the-art brain-computer interface signal processing. Journal of Neural Engineering 2011; 8(2): 1-8.
10. Keeser D, Padberg F, Reisinger E, Pogarell O, Kirsch V, Palm U, Karch S, Moller HJ, Nitsche MA, Mulert C. Prefrontal direct current stimulation modulates resting EEG and event-related potentials in healthy subjects: A standardized low resolution tomography (sLORETA) study. NEUROIMAGE 2011; 55(2): 644- 657.
11. Koles ZJ. Head modeling for E/MEG source analysis: Image segmentation, domain decomposition and solution of the forward problem. Joint Meeting Of The 6th International Symposium On Noninvasive Functional Source Imaging Of The Brain And Heart And The International Conference On Functional Biomedical Imaging 2007: 354-355.
12. Acar ZA, Makeig S. Neuroelectromagnetic Forward Head Modeling Toolbox. Journal of Neuroscience Methods 2010; 190(2): 258-270.
13. Binnie C D, Dekker E, Smit A, and Van der Linken G. Practical considerations in the positioning of EEG electrodes. Electroencephalogr. Clin. Neurophysiol. 1982; 53(4): 453–458.
14. De Munck JC, Vijn PCM, and Spekreijse H. A practical method for determining electrode positions on the head. Electroencephalogr. Clin. Neurophysiol. 1991; 78(1): 85–87.
15. Khosla D, Don M. and Kwong B. Spatial mislocalization of EEG electrodes - effects on accuracy of dipole estimation, Clinical Neurophysiology 1999; 110: 261- 271.
16. Le J, Lu M, Pellouchoud E, and Gevins A. A rapid method for determining standard 10/10 electrode positions for high resolution EEG studies. Electroencephalogr. Clin. Neurophysiol. 1998; 106: 554–588.
17. Koessler L, Cecchin T, Caspary O, Benhadid A, Vespignani H, Maillard L. EEG-MRI Co-registration and  Sensor Labeling Using a 3D Laser Scanner. Annals of Biomedical Engineering 2011; 39(3): 983-995.
18. Whalen C, Maclin EL, Fabiani M, Gratton G. Validation of a Method for Coregistering Scalp Recording Locations With 3D Structural MR Images. Human Brain Mapping, 2008; 29 (11) 1288-1301.
19. Sijberg J, Vanrumste B, Van Hoey G, Boon P, Verhoye M and Van der Linden A. Automatic localization of EEG electrode markers within 3D MR data. Magn. Reson. Imaging 2000; 18: 485-488.
20. Yoo SS, Guttmann C, Ives J, Panych L, Kikinis R, and Schomer D. 3D Localization of surface 10–20 electrodes on high resolution anatomical MR images. Electroencephalogr. Clin. Neurophysiol. 1992; 102: 335–339.
21. Koessler L, Benhadid A, Maillard L, Vignal JP, Felblinger J, Vespignani H, and Braun M. Automatic localization and labeling of EEG sensors (ALLES) in MRI volume. Neuroimage 2008; 41(3): 914-923.
22. Koessler L, Maillard L, Benhadid A, Vignal JP, Braun M, and Vespignani H. Spatial localization of EEG electrodes. Clin. Neurophysiol. 2007; 37: 97-102.
23. Russell GS, Eriksen KJ, Poolman P, Luu P, and Tucker DM. Geodesic photogrammetry for localizing sensor positions in dense-array EEG. Clin Neurophysiol 2005; 116:1130-1140.
24. Baysal U and Sengül G. Single Camera Photogrammetry System for EEG electrode Identification and Localization. Annals of Biomedical Engineering 2010; 38(4): 1539–1547.
25. Qian S, Sheng Y. A Single Camera Photogrammetry System for Multi-angle Fast Localization of EEG Electrodes. Annals of Biomedical Engineering 2011; 39 (11): 2844-2856.
26. Bao JZ, Lu ST and Hurt WD. Complex dielectric measurements and analysis of brain tissues in the radio and microwave frequencies. IEEE Trans.Microwave Theory Tech. 1997; 45: 1730-1741.
27. Foster KR, Schepps JL, Stoy RD and Schwan HP. Dielectric properties of brain tissue between 0.01 and 10 GHz. Phys Med Biol 1979; 24: 1177-–1187
28. Baumann SB, Wozny DR, Kelly SK and Meno FM. The electrical conductivity of human cerebrospinal fluid at body temperature. IEEE Trans Biomed Eng 1997; 44: 220-223.
29. Sengul G, Baysal U. An extended Kalman filtering approach for the estimation of human head tissue conductivities by using EEG data: a simulation study. Physiological measurement 2012; 33(4): 571-586
30. Baysal U and Haueisen J. Use of a priori information in estimating tissue resistivities application to human data in vivo. Physiol. Meas. 2004; 25: 737-748
31. Akhtari M et al. Conductivities of three layer live human skull. Brain Topography.2002; 14: 151-167.
32. Değirmenci E, and Eyüboğlu BM. Anisotropic conductivity imaging with MREIT using equipotential projection algorithm. Physics in Medicine and Biology 2007; 52: 7229 -7247.
33. Arpinar VE, Hamamura MJ, Degirmenci E , Muftuler LT. MREIT experiments with 200 muA injected currents: a feasibility study using two reconstruction algorithms, SMM and harmonic B-Z. Physics In Medicine And Biology 2012; 57(13): 4245-4261.
34. Van Hoey G, Vamrumste B, D'Have M, Van de Walle R, Lemahieu I, and Boon P. Infuence of measurement noise and electrode mislocalization on EEG dipolesource localization. Med. Biol. Eng. Comput. 2000; 38: 287-296.
35. Wang Y, and Gotman J. The influence of electrode location errors on EEG dipole source localization with a realistic head model. Clinical Neurophysiology 2001; 112: 1777-1780.
36. Whittingstall K, Stroink G. and Dick B. Dipole localization accuracy using grand-average EEG data sets. Clinical Neurophysiology 2004; 115: 2108-2112.
37. Pohlmeier R, Buchner H, Kno U, Rienajcker G, Beckmann A, and Pesch, J. The influence of skull – conductivity misspecification on inverse source localization in realistically shaped finite element head models. Brain Topography 1997; 9: 157-162.
38. Awada KA, Jackson R D, Williams S, Baumann B, Wilton JT, Fink DR, and Prasky BR. Effect of conductivity uncertainties and modeling errors on EEG source localization using a 2-D model. IEEE Trans. Biomed. Eng. 1998; 45: 1135-1145.
39. Vanrumste B. EEG dipole source analysis in a realistic head model, PhD thesis, University of Gent, 2000.