Research Article - Biomedical Research (2016) Volume 27, Issue 4

Computational modeling of amperometric choline biosensor for neurochemical detection

¹Department of Biomedical Engineering, Velalar college of Engineering and Technology, Erode -638012, India

²Department of Computer Science Engineering, Nandha Engineering college, Erode -638052, India

*Corresponding Author:

P Ravikumar
Department of Biomedical Engineering, Velalar College of Engineering and Technology, India

Accepted on April 15, 2016

Abstract

The behavior of biosensors is based on the well-defined physical, chemical and biological reactions, which are expressed by nonlinear differential equations. The characteristics of diffusion reaction of choline biosensor are analyzed mathematically for wide range of input parameters such as initial concentration of choline and thickness of choline oxide enzyme layer. The mathematical simulations are done in MATLAB software using partial differential equation solver pdepe function. The analytical results are compared with numerically simulated results for various conditions to validate the model parameters. A numerical simulation result shows less than 2% deviation from analytical results for various substrate concentrations. For dimensionless diffusion distance x=0 and sigma=1, the dimensionless substrate and product concentrations are 0.72 and 0.18 when t=1 and changes exponentially with time.

Keywords

Choline, Biosensor, Pdepe, Mathematical modeling, MATLAB.

Introduction

Biosensor is a compact analytical device, used for detection of very minute amount of chemical elements present in the living systems [1]. Now a days biosensor plays a very important role in disease detection especially in neurochemical detection [2]. The concentrations of neurochemicals are very minute and difficult to detect due to poor sensitivity and selectivity of conventional detection methods [3,4]. Choline is an essential component for functioning of cell and precursor for acetylcholine. The neuro transmitter choline and acetylcholine are mainly involved in Alzheimer disease [5]. Biosensors are potentially useful for quick detection of chemical components. The development of these biosensing systems depends on a quantitative measurement of the enzyme activity before and after exposure to a target substrate [6].

In recent days amperometric based electrochemical biosensors are highly used for fast and accurate detection [7,8]. The operations of electrochemical sensors are very simple and never affect the host material [9,10]. Amperometric biosensors, produces the output current based on the sensing materials on the working electrode act as a catalyst and catalyze the redox reaction. During measurement, the electrode potential is kept constant while the current is monitored. Optimization of biosensor is the time consuming process, for that mathematical modeling is used to reduce the optimization time, cost and optimize the analytical characteristics of actual biosensor [11-13].

The nonlinear problems in enzyme diffusion for different types of biosensors are solved using various numerical methods [14] and analytical methods [15,16]. Mathematical Modeling of amperometric enzyme biosensor based on finite difference scheme was reported for glucose detection [13-19]. The mathematical simulation at transient and steady state conditions are carried out using the finite difference scheme technique. The amperometric biosensor response is numerically analyzed by changing the model parameters.

Mathematical Modelling

The amperometric choline biosensor was constructed using three electrode system with platinum based choline working electrode, Ag/Agcl reference electrode and platinum counter electrode. The following enzyme reaction takes place in working electrode [5].

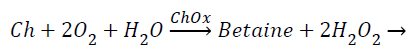(1)

The enzyme reaction for the above equation can be written as

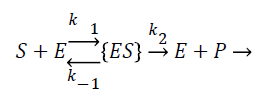(2)

Where E is the choline oxidase enzyme, S is the choline substrate, ES is a transitory complex assumed to be at a steady concentration, and P is the hydrogen peroxide product. The k₁, k_-1, k₂ are the reaction rate constants. The mass balance equation for the above reaction in the enzyme layer can be written using Fick’s second law,

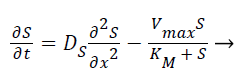(3)

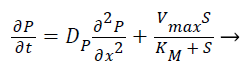(4)

Where S and P represent concentrations of substrate and product, D_S and D_P are the corresponding diffusion coefficients. V_max is the maximum enzymatic rate when the enzyme is fully saturated; K_M is the Michaelis Menten constant. For enzyme reaction, the output current produced by the sensor is

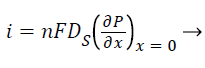(5)

Where n is the number of electrons involved in charge transfer and F is the Faraday constant.

Dimensionless form

The following parameters are used to convert the above Equations 3 and 4 into normalized form.

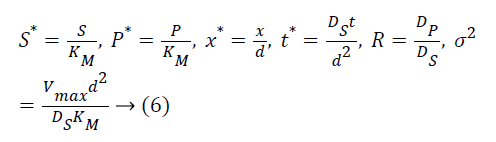
The Equations 3 and 4 reduce to the following dimensionless form

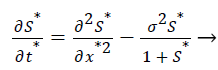(7)

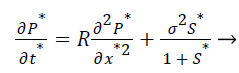(8)

σ², the Damkohler number (Da), compares the diffusion rate through the enzyme layer with the enzyme reaction rate. If Damkohler less than one, then the enzyme kinetics controls the biosensor response.

The dimensionless initial and boundary conditions are

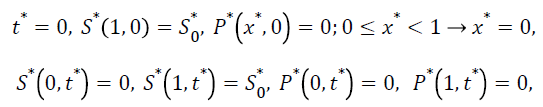
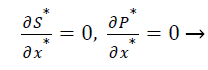(9)

The closed form expression for the current density from Equation 5,

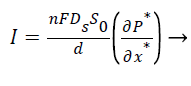(10)

Numerical simulation

The partial differential Equations 7 and 8 for the corresponding initial and boundary conditions are solved numerically using pdepe function in MATLAB software [20]. The partial differential equations are solved using finite difference schemes. Numerical solutions are obtained for various parameters such as initial substrate concentrations, ration of reaction diffusion, and sigma for every value of time and space vector.

Result and Discussion

Model validation

The analytical solutions are validated for specific set of values [21]. In this paper the numerically simulated data are validated through analytical solutions for output current density. The following parameters are used for simulation F=96.486 C/ mmol, n=2, V_max=100 μmol, KM=3 mmol, d=100 μm, DS=1x10^-9 m²/s [19,21].

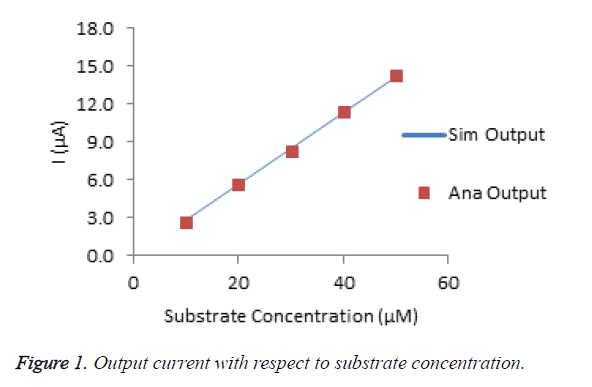
The Figure 1 shows the amperometric response of choline biosensor for various substrate concentrations. The percentage of deviation of analytical from simulated result is calculated that is less than 2%. It conforms that, the modeled data are very much similar to experimental data.

Figure 1. Output current with respect to substrate concentration.

Sensor response

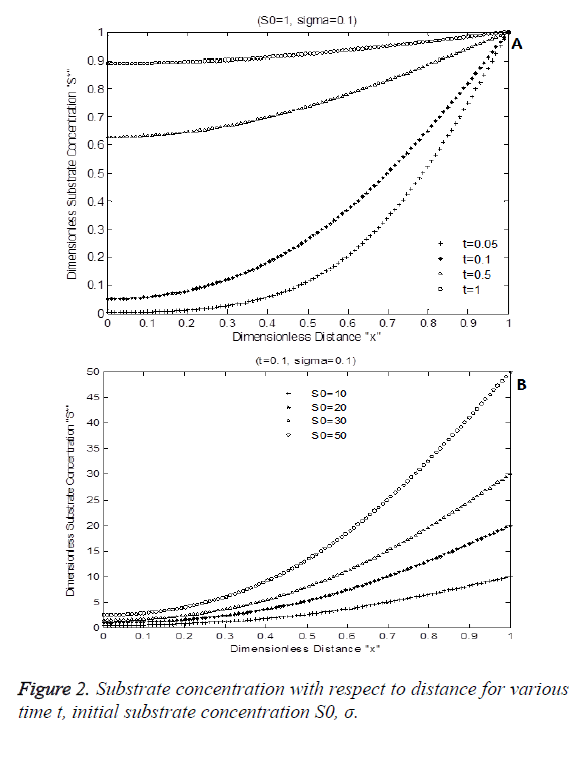
Figure 2 shows the numerical simulation result of Equation 7. Figure 2A indicates the diffusion activity of the substrate with respect to time for constant Damkohler number sigma=0.1 with initial substrate concentration of 1. Figure 2B shows the dimensionless substrate concentration for various levels dimensionless choline level. S* is increased due to various initial substrate content S0. It increases exponentially with respect to time and distance.

Figure 2. Substrate concentration with respect to distance for various time t, initial substrate concentration S0, σ.

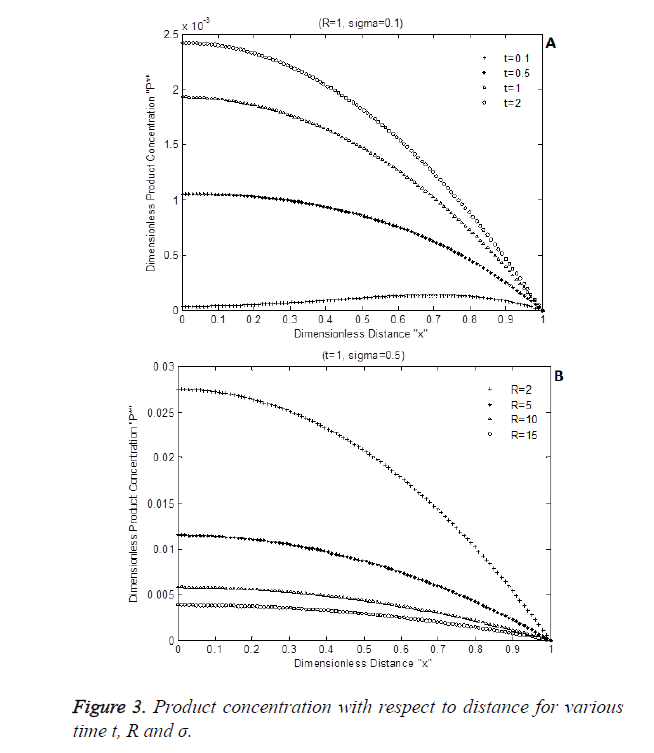
The numerical simulation output of Equation 8 is shown in Figure 3 shows the dimensionless product P* with respect to dimensionless enzyme thickness for various Damkohler number and diffusion coefficients rate R. Figure 3A and Figure 3B shows that product concentration P* reduces when diffusion coefficient ratio or time t increases.

Figure 3. Product concentration with respect to distance for various time t, R and σ.

Conclusion

The one dimensional computational model of choline biosensor was simulated for substrate conversion and various parameters that influence the diffusion of substrate and product. The Damkohler number (σ²) mainly influences the output current density. The numerical result of output current was compared with analytical result, and there was no significant difference between the numerical result and analytical result. This study will help the researchers in biosensor filed to study the behavior of biosensor before actual experimentation.

References

1. VoDinh T. Biosensors and Biochips-BioMEMS: In: Biomedical Nanotechnology. Springer, Germany 2007; 1-20.
2. Ferreira AAP, Uliana CV, de Souza Castilho M, Pesquero NC, Foguel MV, dos Santos GP, Fugivara CS, Benedetti AV, Yamanaka H. Amperometric Biosensor for Diagnosis of Disease: In: State of the Art in Biosensors-Environmental and Medical Applications. InTech Publisher, Croatia, 2013; 253-289.
3. Baoyan Wu, Zhongmin Ou, Xiaojuan Ju, Shihua Hou. Carbon Nanotubes/Gold Nanoparticles Composite Film for the Construction of a Novel Amperometric Choline Biosensor. J Nanomaterials 2011; 46: 1-6.
4. Perry M, Li Q, Kennedy RT. Review of recent advances in analytical techniques for the determination of neurotransmitters. Anal ChemActuator 2009; 653: 1-22.
5. Mitchell KM. Acetylcholine and Choline Amperometric Enzyme Sensors Characterized in Vitro and in Vivo. Anal Chemistry 2004; 76: 1098-1106.
6. Grieshaber D, MacKenzie R, Voros J, Reimhult E. Electrochemical Biosensors - Sensor Principles and Architectures. Sensors 2008; 8: 1400-1458.
7. Hristov SM. Amperometric biosensors. Bulgarian Chem Communications 2008; 40: 204-210.
8. Yogeswaran U, Shen-Ming Chen. A Review on the Electrochemical Sensors and Biosensors Composed of Nanowires as Sensing Material. Sensors 2008; 8: 290-313.
9. Chen C, Xie Q, Yang D, Xiao H, Yingchun F, Yueming T, Shouzhuo Y. Recent advances in electrochemical glucose biosensors: a review. RSC Adv 2013; 3: 4473-4491.
10. Mell LD, Maloy JT. A model for the amperometric enzyme electrode obtained through digital simulation and applied to the immobilized glucose oxidase system. Anal Chemistry 1975; 47: 299-307.
11. Baronas R, Kulys J, Petrauskas K, Razumiene J. Modelling Carbon Nanotubes-Based Mediatorless Biosensor. Sensors 2012; 12: 9146-9160.
12. Dzyadevych SV, Soldatkin AP, Korpan YI. Biosensors based on enzyme field-effect transistors for determination of some substrates and inhibitors. Anal BioanalChem 2003; 3: 496-506.
13. Neykov A, Rangelova V. Mathematical Modeling of the Biosensor Systems. Biotechnology & Biotechnological Equipment 1998; 12: 100-109.
14. Ganesan SP, Saravanakumar K, Rajendran L. Mathematical Modeling of Multienzyme Biosensor System. Int J Comput Mathematics 2014.
15. Praveen T, Rajendran L. Theoretical Analysis of an Amperometric Biosensor Based on Parallel Substrates Conversion. ISRN Electrochemistry 2014.
16. Anitha A, Anitha S, Rajendran L. A Kinetic Model for Amperometric Biosensor at Mixed Oxidase Enzyme. Int J Electrochem Sci 2014; 9: 990-1002.
17. Gaidamauskaite E, Barona R. A Comparison of Finite Difference Schemes for Computational Modelling of Biosensors. Nonlinear Anal Modelling Control 2007; 12: 359-369.
18. Fransaer J, Ammam M. Mathematical Modeling of the Amperometric Response to Glucose of Glucose Oxidase Films Deposited by AC-Electrophoresis. J Sensor Technol 2011; 1: 17-21.
19. Yang WY, Cao W, Chung TS, Morris J. Applied Numerical Methods using MATLAB. John Wiley & Sons, Inc., 2005.
20. Aseris V. Computational Modelling of Wire Biosensor with Competitive Substrates Conversion. Proceedings of the World Congress on Engineering 2014.
21. Qiang WZ, Jia JZ, Wang K, Juan JX, Chen HY, Xia XH. Exploration of Two-Enzyme Coupled Catalysis System Using Scanning Electrochemical Microscopy. Anal Chem 2012; 84: 10586-10592.