Research Article - Biomedical Research (2017) Volume 28, Issue 13
Automatic hybrid ventricular segmentation of short-axis cardiac MRI images
Nageswararao AV1*, Srinivasan S1 and Babu Peter S2
1Department of Instrumentation Engineering, Madras Institute of Technology Campus, Anna University, Chennai, India
2Barnard Institute of Radiology, Madras Medical College and Rajiv Gandhi Government General Hospital, Chennai, India
- *Corresponding Author:
- Nageswararao AV
Department of Instrumentation Engineering
Madras Institute of Technology Campus, Anna University, India
Accepted on May 17, 2017
Abstract
Ventricular segmentation is an important task to quantitatively evaluate the function of the cardiovascular system in Cardiac Magnetic Resonance (CMR) images. In this work, an automatic hybrid segmentation method is proposed in which Kirsch edge detection method is combined with modified Local Region based Chan-Vese (LRCV) method. The edge transformed image obtained from the Kirsch operator is provided to the modified LRCV method with distance regularized level set for segmenting the ventricles. Segmentation results shows that the hybrid method performs better than conventional Local Chan-Vese (LCV), Local Binary Fitting (LBF), Local Global Active Contour (LGAC), Locally Statistical Active Contour (LSAC), LRCV and semi-automatic methods both qualitatively and quantitatively by dice metric coefficient, Jaccard Index, modified Hausdroff distance, sensitivity and specificity. Further, the proposed hybrid method is evaluated based on End systolic volume, End diastolic volume and ejection fraction using Bland-Altman plot. The analytical results show that the automatic Kirsch hybrid method provides better segmentation to evaluate the diagnostic parameters.
Keywords
Cardiac MRI, Ventricular segmentation, Edge detection, Region growing, Local region based Chan-Vese, Bland-Altman plot.
Introduction
Over the years, different sorts of medical imaging like ultrasound, computed tomography, Magnetic Resonance Imaging (MRI) [1,2] and molecular imaging have been developed. Among them, MRI has an edge over the other methods in providing high contrast 3D data and has no known irreversible biological effects in humans. Cardiac Magnetic Resonance (CMR) [3] is one of the preferred techniques for imaging patients with heart diseases. It provides information about cardiovascular anatomy and many diagnostic parameters like ventricular size, mass, wall thickness and blood flow measurements [4,5].
There are various methods available in the literature for segmenting [6,7] left ventricle due to its key function in the heart. Compared to left ventricle, less attention is given for the delineation of right ventricle that is vital in diagnosing certain cardiovascular diseases (like Arrhythmogenic Right ventricular dysplasia and hypertension) [8]. Right ventricle segmentation is more challenging due to its complex variable shape motion and uneven borders. There is an online right ventricle segmentation challenge conducted by Medical Image Computing and Computer Assisted Intervention (MICCAI) 2012 conference. In this competition, seven different semiautomated [9,10] and automated methods are selected for the segmentation of right ventricle in CMR images.
Zuluaga et al. proposed a multi-atlas segmentation method in which there are different propagation levels. To further improve the registration, the result at each propagation level is used as a mask for initializing the registration. The computational time per patient is 720 s. Bai et al. proposed a 3D multi-atlas based segmentation method that uses multiple atlases for labeling different landmarks in the target image. Bspline non-rigid image registration is used to combine the local weighted labels with the atlas labels for estimating the target labels. The computation time per patient is minimized by about 300 s with parallel execution.
Semi-automated segmentation method based on region growing has been developed [11,12], but needs manual intervention for placing an initial contour around the ventricles. Adams et al. [13] have shown that the initialization of seed point selection is very important in region growing method. Yu et al. [14] have discussed the drawbacks in boundary detection using region growing and emphasized the need for combining edge detection with region growing for precise segmentation. A review on segmentation methods for short axis CMR images had been presented by Yu et al. [15].
Active contour methods which depend on energy for surface evolution are classified as edge based active contour methods and region based active contour methods. Region based active contour methods, which use statistical information are more advantageous, compared to edge based active contour methods in detecting objects with weak boundaries [16]. One of the most frequently used region-based methods is Chan-Vese (CV) method [17,18] which assumes, that intensity in each region of an image is statistically homogeneous. However, the CV method does not work well for the images with intensity inhomogeneity. To overcome this problem, several improvements have been made to the CV method. Local Chan- Vese (LCV) method [19] is developed based on local statistical functions and level set theory. The LCV method is efficient for two phase segmentation i.e. segmenting foreground and background, but it fails in detecting objects with different intensities. Li et al. [20,21] proposed a modified method by including local intensity information for intensity inhomogeneity image segmentation. This method is sensitive to the initial contour location and complex computations are involved. Zhang [22] proposed a region based active contour model known as Selectivse Binary and Gaussian Filtering Regularized Level Set, which uses a signed pressure force. Zhang [23] proposed a linear binary fitting model that uses spatial varying function for approximating the local intensities. However, this model is sensitive to the initial location of the contour and gets easily trapped into local minima.
Wang et al. [24,25] identified the boundaries by considering both local and global intensity information. The derived local and global forces from the intensity information assist in initialization and stopping of the contour respectively. The problem is that the position of the contour has to be properly selected. Liu et al. [26] developed a Local Region based Chan- Vese (LRCV) method, where the degraded CV output is considered as an initial contour to the next stage. Even though, it effectively segment intensity inhomogeneity images, the effectiveness of the output depends on the placement of the initial contour.
The combination of regional information provided by the edge gradient and global information provided by region based methods gives accurate delineation of a particular region of interest in intensity inhomogeneous images. Conventional edge based and region based methods can’t give exact segmentation results of inhomogeneity images independently. Hence, there is a need for a simple and accurate hybrid segmentation method for segmenting inhomogeneity CMR images without any over or under segmentation [2,28].
The rest of the paper is organized as follows. Section 2 gives a general overview of Kirsch edge detection and Region based active contour methods. This section also discusses about the evolving of the proposed Kirsch hybrid method. In the first part of section 3 the performance of different region based methods, such as Local Chan-Vese (LCV), Local Binary Fitting (LBF), Local Global Active Contour (LGAC), Locally Statistical Active Contour (LSAC) and LRCV are carried out for ventricular detection. Further, based on the performance metrics Kirsch edge based method is preferred from other edge based methods (Sobel, Canny, Demirel and Edge color) to develop a hybrid method with LRCV method. The developed automatic Kirsch hybrid method is also compared with the conventional semi-automatic and manual segmentation methods in terms of systolic, diastolic volumes and ejection fraction of both left and right ventricles. Section 4 gives the conclusion.
Image acquisition
Analysis is carried out using 25 data sets that consists of both normal and abnormal short-axis CMR images obtained from 3T MR imaging unit (Magnetom Symphony, Siemens Medical Solutions, Erlangen, Germany) of Rajiv Gandhi Government General Hospital, Park Town, Chennai. Using steady state free precession protocol, a stack of 20-30 contiguous short-axis slices covering both the ventricles from base to apex are obtained for a repetition time of 3.4 ms and echo time of 1.7 ms respectively. The size of the slice is 174 × 208 with a thickness of 7 mm.
Kirsch edge detection
Kirsch edge detection method [29] is one of the techniques that find the maximum edge strength in a predetermined direction. The edge gradient of the Kirsch operator is given by
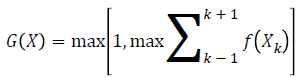
where f (Xk) represents eight neighbouring pixels of X and the subscript k is computed by modulo 8. The Kirsch edge detection method uses spatial filters in eight different directions. A compass kernel with a single kernel mask of size 3 × 3 at 0º is given as
K1=(5 5 5; -3 0 -3; -3 -3 -3) → (2)
K2, K3, K4, K5, K6, K7 and K8 are the remaining seven kernels obtained by shifting the kernel K1 with an increment of 45º through all compass directions, i.e., N, NW, W, SW, S, SE, E, and NE. The input image is convolved with eight templates and by sliding the mask over the entire image, the final edge transformed output image is considered as Ik.
Region based active contour
Region based active contour methods make use of statistical information and the initial contour can begin anywhere in the image for detecting interior and exterior boundaries efficiently.
The Chan-Vese (CV) model is a special case of the Mumford-
Shah problem. Given the curve 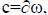 with
with 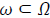 being an
open subset, of the image
being an
open subset, of the image 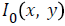 in the image domain Ω, the energy function of the image is minimized as follows
in the image domain Ω, the energy function of the image is minimized as follows
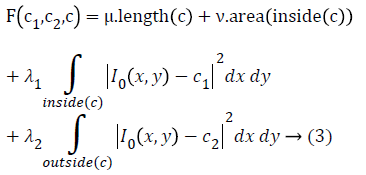
where the constants μ-Smoothing parameter, v-Propagation speed and λ1, λ2-Inside and outside driving force. c1, c2 are the average intensities that exist inside and outside the contour c and it is represented as
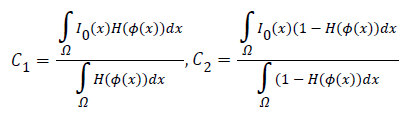
The energy function F (c1, c2, c) is minimized with level set function Ø(x, y) as follows
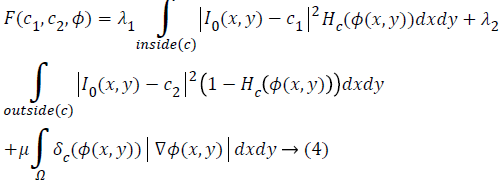
where H (Ø) is the Heaviside function, δ (Ø) is the Dirac function and ∇ is the gradient operator. In a level set function
domain, Heaviside function is 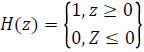
while δ (z)=dH (z)/dz being Dirac function.
The proposed kirsch hybrid method
In the proposed automatic Kirsch hybrid method, the weighted average intensities inside and outside the contour at a point p1 is approximated by a neighborhood point p1, where p1, p2 ϵ R2 and Ω is a subset of R2 for the original image I.
In Kirsch detection method, the kernel masks are obtained by considering a single mask and rotating it in eight compass directions. The final image obtained by the Kirsch operator is Ik and the energy function in Equation 3 can be rewritten as:
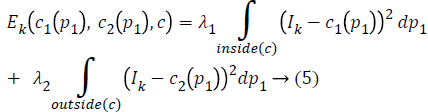
The two constants c1 and c2 in CV are replaced by spatially varying functions c1 (p1) and c2 (p1) which can be given as
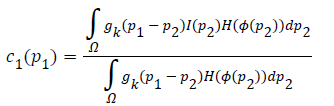
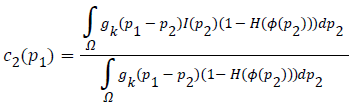
where gk is the Gaussian kernel function and gk (p1-p2) is the weight allocated to each intensity of I (p2) at p2.
In level set methods, an evolving curve c is represented by Lipschitz function . This is selected such that it is positive inside c and negative outside c. The modified energy function can be written as
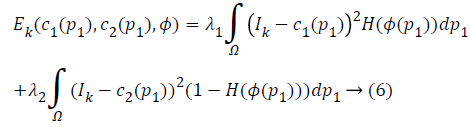
where H is Heaviside function.
Further, the stability of the level set function is preserved by re-initializing it from the degraded shape, by introducing a distance regularization term in the level set formulation of LRCV method. As proposed by Li et al. [30], the level set regularization term has both forward and backward diffusion effect, which is defined as
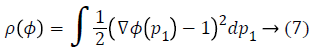
Thus, from Equation 6, the minimized energy function is obtained as
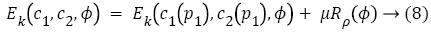
The level set regularization term Rρ (Ø) is defined as
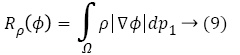
where ρ is energy density function.
The energy function in Equation 8 is minimized by Euler- Lagrange equation to obtain the gradient descent flow as
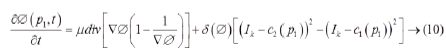
where μ, λ1 and λ2 are fixed parameters.
Validation
The validation of the proposed Kirsch hybrid segmentation method is done using Dice Metric (DM) and Modified Hausdroff Distance (MHD). The DM measures set of agreements between the images which is given by the equation
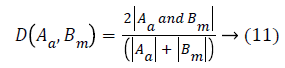
where A and Bm are automatically (proposed method) and manually segmented contours respectively. The value 0 indicates no overlap and 1 indicates a perfect agreement between any two methods. Dubuission and Jain [31] revised Hausdroff Distance (HD) metric by proposing an improved measure called the MHD, that is sensitive to small perturbations in point locations for shape alignment. As the difference between the two sets of points increases, its value increases monotonically. MHD performs better than HD by computing the forward and reverse distances that give the output as the minimum for both the sets A and B as
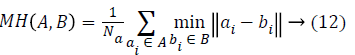
where a and b are coordinates of a point on the curve represented by an ordered pair ai, bi and Na is the number of points in the set A.
Results
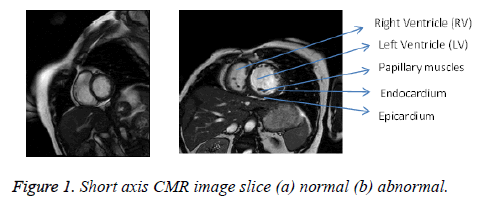
The short axis CMR images with normal and abnormal ventricles are shown in Figure 1. The main objective of this work is to segment both left and right ventricles simultaneously. The major challenges in ventricular segmentation are its small size with crescent shape, change in size during systolic and diastolic phases, presence of papillary muscles near the left ventricle and inhomogeneity. In order to consider all these issues while segmenting, a new automatic Kirsch hybrid method combining edge and region based methods is proposed.
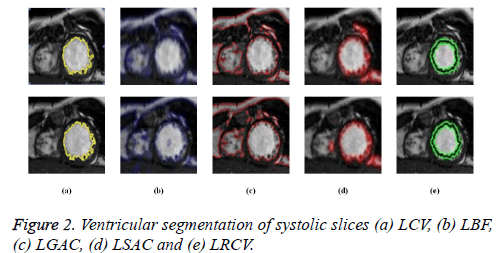
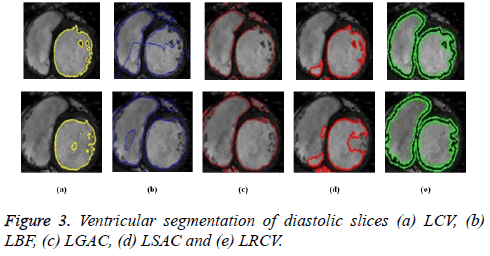
Region based active contour methods, which are good at segmenting weak boundaries are used to segment both LV and RV. There are different variants in the region based active contour methods right from the beginning of CV method. The performance of different region based active contour methods such as LCV, LBF, LGAC, LSAC and LRCV are compared and its results are shown in Figures 2 and 3.
As seen from Figures 2a and 3a, LCV segments only LV portion in both systolic and diastolic slices. Figures 2b and 3b shows the segmented output by LBF method. LGAC method segments adjacent objects as observed from Figures 2c and 3c, even for an appropriate chosen value of α. It can be inferred from Figures 2d and 3d that LSAC method is unable to detect the ventricles exactly, because its performance depends on the location of the initial contour. The results in Figures 2e and 3e demonstrate that LRCV method gives accurate results for diastolic slices, but it fails to segment the right ventricle.
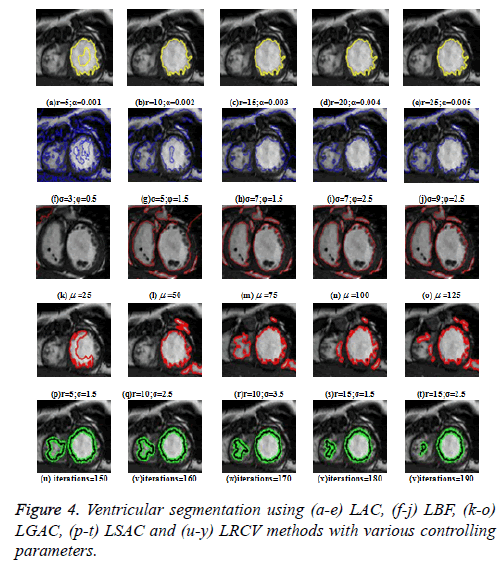
Figure 4 shows the segmented results of these methods based on their controlling parameters. In LAC method, the output varies with respect to the change in localization radius r and weight of smoothing term α. The Lower value of r (5) as in Figure 4a indicates a more local region, whereas a higher value of r (25) as in Figure 4e indicates a more global region and can give a better segmentation output of the ventricles. The Higher value of α (0.005) gives a smoother output as shown in Figure 4e.
In LBF and LSAC methods, σ is the scaling parameter and it should be tuned properly to give a moderate output as shown in Figure 4j and 4r. A higher value of ϕ (2.5), the variance of the regularized Gaussian kernel and σ (9) in LBF gives a better segmentation result as shown in Figure 4j. In LSAC method, the change in r value gives a different output and the value should be moderate to give a better output as shown in Figure 4r. In LGAC, the local and global energy terms are dynamically balanced by adjusting the calculated weight on the local intensity. μ is the controlling parameter that should be varied and higher value gives a better output as shown in Figure 4o. The segmentation of RV in LRCV method varies with the number of iterations and as the number of iterations increases, the contour gets trapped in local minima in the RV as shown in Figure 4y.
The results are validated by Jaccard Index (JI), Sensitivity (SN) and Specificity (SP) parameters. The results from Table 1 show that the LRCV method has a higher correlation with the manual results, as JI approaches one. SN and SP represent the percentage of true positive and true negative ratio and a higher percentage of SN and SP for LRCV method indicates that it gives better segmentation results, compared to other methods.
| Algorithm | Systole | Diastole | ||||
|---|---|---|---|---|---|---|
| JI | SN (%) | SP (%) | JI | SN (%) | SP (%) | |
| LCV | 0.76 | 42 | 41 | 0.78 | 51 | 58 |
| LBF | 0.74 | 39 | 40 | 0.72 | 49 | 57 |
| LGAC | 0.75 | 38 | 41 | 0.72 | 48 | 55 |
| LSAC | 0.73 | 39 | 41 | 0.71 | 50 | 59 |
| LRCV | 0.86 | 47 | 45 | 0.87 | 61 | 60 |
Table 1. Validation of segmentation methods.
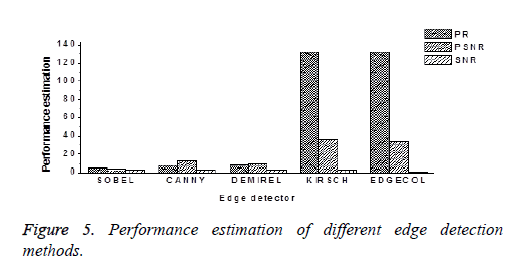
Even though LRCV method can segment left ventricle in most of the cases, it fails to segment RV. Hence to improve the performance of segmentation, there is a need for considering the edge gradient information along with region details. In order to decide on an excellent edge detection technique for combining with region based active contour method, various edge detection techniques such as Sobel, Canny, Demirel, Kirsch and Edge color are applied. The performance analysis of the different edge detection techniques in terms of PR, PSNR and SNR is shown in Figure 5. The PR which states the ratio of true to false pixels is as high as 99% for Kirsch and edge color methods. Even though, PR is almost similar for both methods, PSNR and SNR are higher for the Kirsch edge detector method. Hence, it is proposed to combine Kirsch operator with modified LRCV method for automatic segmentation of both left and right ventricles.
The performance of the Kirsch hybrid method is compared with semi-automatic method proposed by Souto [8]. In semiautomatic method, prior to applying region growing method, canny edge detection and iterative threshold on the edge detected image were performed. The segmented systolic and diastolic slices of LV and RV by the Kirsch hybrid method and semi-automatic method are shown in Figures 6 and 7. It is observed that, the proposed automatic hybrid segmentation method is able to segment the left ventricles in both systolic and diastolic conditions. In case of semi-automatic method, the performance of the region growing method depends on the seed point selection.
The proposed Kirsch method is compared with the conventional methods of LCV, LBF, LGAC, LSAC, LRCV and semi-automatic methods with validation parameters shown in Table 2. Table 2 gives the average values of DM, JI, MHD, SN and SP for both systolic and diastolic phases. Based on the observation from Table 2, it can be noted that the DM of Kirsch hybrid method is high, as it has better similarity with ground truth than the semi-automatic method. MHD which gives similarity distance measure is least for Kirsch hybrid method than semi-automatic method, and it also confirms that it is much more similar to manual segmentation. The proposed Kirsch hybrid method presents similar contour delineations as that of manual segmentation in case of both systolic and diastolic phases due to the value of DM and JI nearly equal to 1.
| ALGORITHM | ||||||||
|---|---|---|---|---|---|---|---|---|
| LCV | LBF | LGAC | LSAC | LRCV | Semi-automatic | Hybrid | ||
| Systole | DM | 0.45 | 0.47 | 0.44 | 0.47 | 0.85 | 0.8 | 0.88 |
| JI | 0.33 | 0.34 | 0.31 | 0.33 | 0.75 | 0.73 | 0.81 | |
| MHD | 2.85 | 2.51 | 2.76 | 2.58 | 1.44 | 1.64 | 1.54 | |
| SN (%) | 38 | 39 | 38 | 39 | 46 | 44 | 46 | |
| SP (%) | 55 | 40 | 41 | 39 | 41 | 40 | 42 | |
| Diastole | DM | 0.31 | 0.34 | 0.32 | 0.36 | 0.77 | 0.82 | 0.9 |
| JI | 0.18 | 0.21 | 0.19 | 0.22 | 0.62 | 0.74 | 0.83 | |
| MHD | 2.69 | 1.61 | 2.21 | 1.58 | 1.68 | 1.59 | 0.8 | |
| SN (%) | 40 | 51 | 41 | 52 | 61 | 60 | 62 | |
| SP (%) | 60 | 59 | 60 | 59 | 60 | 51 | 53 | |
Table 2. Validation of Kirsch hybrid method with the conventional segmentation methods.
Further to quantitatively aid the cardiologists in the diagnosis of cardiovascular diseases, various indices like End Systolic Volume (ESV), End Diastolic Volume (EDV) and Ejection Fraction (EF) which occur at the time of maximum contraction and maximum expansion of the heart are obtained. Statistical measures such as p and r values that basically determine the deviation of the obtained results from the expected results are calculated. It is found that there is no statistical significant difference (p>0.05) between the proposed Kirsch hybrid method and manual method for ESV, EDV and EF of LV segmentation. The Pearson correlation coefficient, (r>0.93) which gives the linear dependence is also high. In case of RV, there is a high similarity (p>0.05) and a high Pearson correlation coefficient value (r>0.92) for ESV, EDV and EF.
EF is an important measurement in determining how well the heart pumps the blood. A normal range of EF is between 55% and 70%. If the value of EF is less than 40%, it is an indication of cardiomyopathy and it is hypertrophic cardiomyopathy, if its value is higher than 75%. It can be observed from Table 3 that the average values of the ESV, EDV volumes and EF obtained by the Kirsch hybrid method is more similar to the manual segmentation method.
| Volume type | left ventricle | Right ventricle | ||||
|---|---|---|---|---|---|---|
| Kirsch hybrid | Semi-automatic | Manual | Kirsch hybrid | Semi-automatic | Manual | |
| Mean ± SD | Mean ± SD | Mean ± SD | Mean ± SD | Mean ± SD | Mean ± SD | |
| ESV | 43 ± 19 ml | 40 ± 16 ml | 42 ± 19 ml | 48 ± 17 ml | 45 ± 16 ml | 47 ± 17 ml |
| EDV | 116 ± 30 ml | 112 ± 27 ml | 115 ± 31 ml | 150 ± 24 ml | 142 ± 26 ml | 148 ± 25 ml |
| EF | 62 ± 14% | 63 ± 12% | 62 ± 14% | 67 ± 10% | 68 ± 11% | 67 ± 10% |
Table 3. Quantification of LV and RV parameters.
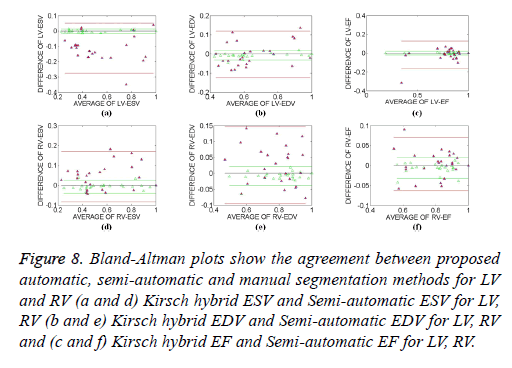
In order to identify the closeness of these methods to that of the manual segmentation method, Bland-Altman plots have been plotted. Normalized values of the ESV, EDV and EF values obtained from the proposed Kirsch hybrid method and semiautomatic method are plotted with the ground truth calculations.
The Bland-Altman method calculates the Mean Difference (MD) between two methods of measurement and provides a 95% limit of agreement of the mean difference (1.96 SD). The smaller the range between these two limits, i.e., the Confidence Interval (CI), better is the agreement with the manual ground truth. The parameters obtained from Bland-Altman plot for proposed Kirsch hybrid method and semi-automatic method is tabulated in Table 4. In semi-automatic method, the MD observed between the parameters is higher than the Kirsch hybrid method. In case of the LV, the range limits (± 1.96 SD) of the ESV, EDV and EF is between (-0.27, 0.12) for a semiautomatic method and (-0.01, -0.02) for a Kirsch hybrid method. From Figure 8, it is also observed that the CI is higher in case of semi-automatic method compared to the automatic Kirsch hybrid method.
| Parameters | Left ventricle | Right ventricle | ||||||
|---|---|---|---|---|---|---|---|---|
| Kirsch hybrid | Semi-automatic | Kirsch hybrid | Semi-automatic | |||||
| MD | CI | MD | CI | MD | CI | MD | CI | |
| ESV | -0.09 | 0.028 | -0.112 | 0.326 | -0.007 | 0.065 | 0.042 | 0.254 |
| EDV | -0.006 | 0.049 | -0.001 | 0.244 | -0.008 | 0.059 | 0.025 | 0.242 |
| EF | 0.001 | 0.041 | -0.016 | 0.290 | 0.006 | 0.051 | 0.004 | 0.133 |
Table 4. Bland-Altman plot parameters.
Figure 8: Bland-Altman plots show the agreement between proposed automatic, semi-automatic and manual segmentation methods for LV and RV (a and d) Kirsch hybrid ESV and Semi-automatic ESV for LV, RV (b and e) Kirsch hybrid EDV and Semi-automatic EDV for LV, RV and (c and f) Kirsch hybrid EF and Semi-automatic EF for LV, RV.
In the case of RV, the range limits (± 1.96 SD) for Kirsch hybrid method is between (-0.03, 0.02) and for semi-automatic method, it is (-0.09, 0.16). Thus, based on the MD and CI, it can be concluded that the parameter estimation of ESV, EDV and EF by the Kirsch hybrid method is better than semiautomatic method.
The proposed Kirsch hybrid method is evaluated in terms of computation time with Mat Lab R2014a using 2.7 GHz Intel I5 processor personal computer. It can be inferred from Table 5 that the proposed Kirsch hybrid method gives faster segmentation output per image slice for both left and right ventricles. The average computational time per patient is 195 s in case of semi-automatic method whereas it takes only 97 s in the proposed Kirsch hybrid method. It is apparent that there is a higher degree of agreement in the end results for the proposed automated Kirsch hybrid method with manual method comparable to that of the semi-automatic method.
| Parameters | Left ventricle | Right ventricle | ||
|---|---|---|---|---|
| Kirsch hybrid | Semi-automatic | Kirsch hybrid | Semi-automatic | |
| ESV | 3.76 s | 7.51 s | 4.47 s | 8.29 s |
| EDV | 3.85 s | 7.52 s | 3.89 s | 8.41 s |
Table 5. Computational evaluation.
Discussion
Ventricular segmentation of CMR images helps the cardiologists to diagnose various cardiovascular diseases; hence accurate delineation of the ventricles is a challenging task. Region based active contour methods such as LCV, LBF, LGAC, LSAC and LRCV are the conventional methods used for ventricular segmentation of CMR images.
LCV method accomplish on global information for contour initialization and local information for drawing the contour towards the edges. It failed to segment RV due to high intensity inhomogeneity, inaccurate edges and due to the placement of contour close to the object boundary. LBF is sensitive to initial contour location and mainly depends on the initialization of the prevailing parameters such as scaling parameter and variance of regularized Gaussian kernel. Computationally it is expensive, as it has to perform four convolution operations and it segments adjacent objects along with the object of interest.
In LGAC, the curve evolution is controlled by the parameter α and its value depends on the size of the object to be detected. LSAC method is good in segmenting intensity inhomogeneity image by bias estimation and correction. The edges of RV cannot be detected easily because of its irregular shape caused due to the presence of muscular bundles in the RV cavity during systolic phases. Validation of all these methods using parameters like JI, SN and SP shows that LRCV method gives better segmentation results compared to other methods.
Edge detection methods such as Sobel, Canny, Demirel, Kirsch and Edge color are analysed using PR, SNR and PSNR, Kirsch edge detector gives better performance. So, a hybrid segmentation method combining Kirsch with modified LRCV method is developed for ventricular segmentation. Results showed that the proposed method gives accurate ventricular delineation when compared to the conventional semi-automatic and manual segmentation methods. The results are further validated using validation parameters like DM and MHD which shows that the proposed method segmentation results matches better with the ground truth. Diagnostic parameters like ESV, EDV and EF calculated from the segmented ventricular portion helps the cardiologists to diagnose various cardiovascular diseases like ventricular hypertrophy.
In this paper, a new automated Kirsch hybrid segmentation method for segmenting both left and right ventricles has been proposed. CMR images are inhomogeneous in nature due to which the segmentation of these images is a challenging task. CMR images, which are the standard reference examination for quantifying the function of heart is a time consuming process with the conventional manual segmentation method, due to the huge amount of data. In order to overcome, the drawbacks in the manual segmentation which is the clinical reference examination procedure, semi-automatic segmentation methods are developed, which still needs some amount of user interaction that may lead to intra and inter-observer variability. Hence, there is a need for automatic segmentation methods which can better delineate both the left and right ventricles.
The comparative analysis of the various edge detection methods shows that the Kirsch edge detector is having a high performance ratio of around 99%. LRCV method segments the ventricles better than other region based active contour methods. Hence, an automatic Kirsch hybrid method is proposed by embedding Kirsch operator for modifying LRCV by regularizing the level set function with a distance regularization term. The validation of the proposed automated Kirsch hybrid segmentation method with semi-automated method was done using different validation parameters. The proposed automatic Kirsch hybrid method gives faster and accurate results for both left and right ventricles with a DM of 0.84 and MHD of 4. The value of DM, nearly equal to 1 indicates a greater similarity between the proposed automatic Kirsch hybrid segmentation outputs with ground truth data. The experimental results indicate that the proposed Kirsch hybrid segmentation method can achieve better ventricular segmentation results.
Acknowledgement
The authors would like to thank, Dr. Babu peter and his team members of Barnard Institute of Radiology (BIR), Madras Medical College (MMC), Chennai, India for providing the CMR images along with their manual delineation, required for this research study.
References
- Hudsmith LE, Petersen SE, Francisc JM, Robsonand MD. Neubauer S. Normal human left and right ventricular and left atrial dimensions using steady state free precession magnetic resonance imaging. J Cardiovasc Magn Reson 2005; 7: 775-782.
- Maceira AM, Prasad SK, Khan M, Pennell DJ. Reference right ventricular systolic and diastolic function normalized to age, gender and body surface area from steady-state free precession cardiovascular magnetic resonance. Eur Heart J 2006; 27: 2879-2888.
- Holloway CJ, Edwards LM, Rider OJ, Fast A, Clarke K, Francis JM, Myerson SG, Neubauer SA. Comparison of visual and quantitative assessment of left ventricular ejection fraction by cardiac magnetic resonance. Int J Cardiovasc Imag 2011; 27: 563-569.
- Morcos P, Vick GW, Sahn DJ, Jerosch-Herold M, Shurman A, Sheehan FH. Correlation of right ventricular ejection fraction and tricuspid annular plane systolic excursion in tetralogy of Fallot by magnetic resonance imaging. Int J Cardiovasc Imag 2009; 25: 263-270.
- Geva T. Repaired tetralogy of Fallot: The roles of cardiovascular magnetic resonance in evaluating pathophysiology and for pulmonary valve replacement decision support. J Cardiovasc Magn Reson 2011; 13: 1-24.
- Paragios N. A variational approach for the segmentation of the left ventricle in cardiac image analysis. Int J Comp Vis 2002; 50: 345-362.
- Jolly MP, Duta N, Funka-Lea G. Segmentation of the left ventricle in cardiac MR images. Proceedings of the Eighth IEEE Intl Conference on Computer Vision 2001; 501-508.
- Goshtasby A, Turner DA. Segmentation of cardiac cine MR images for extraction of right and left ventricular chambers. IEEE Trans Med Imaging 1995; 14: 56-64.
- Zuluaga M, Cardoso M, Modat M, Ourselin S. Multi- atlas propagation whole heart segmentation from MRI and CTA using a local normalized correlation coefficient criterion. Funct Imag Model Heart 2013; 7945: 172-180.
- Bai W, Shi W, Wang H, Peters NS, Rueckert D. Multi-atlas based segmentation with local label fusion for right ventricle MR images. Right Ventricle Segmentation Challenge at MICCAI 2012.
- Masip LR, Tahoces PG, Souto M, Martinez A, Vidal JJ. Semiautomatic quantification of left and right ventricular functions in magnetic resonance imaging. Comput Cardiol 2010; 27: 797-800.
- Miguel S, Lambert RM, Miguel C, Jorge JSC, Amparo MGTP, Jose MC, Pierre C. Quantification of right and left ventricular function in Cardiac MR imaging: Comparison of Semiautomatic and Manual Segmentation Algorithms, Diagnostics 2013; 3: 271-282.
- Adams R, Bischof L. Seeded region growing. IEEE Trans Patt Analysis Mac Vis 1994; 16: 641-647.
- Yu X, Juha YJ. A new algorithm for image segmentation based on region growing and edge detection. IEEE Int Symp Circ Sys 1991.
- Petitjean C, Dacher JN. A review of segmentation methods in short axis cardiac MR images. Med Image Anal 2011; 15: 169-184.
- Cohen LD. On active contour models and balloons. CVGIP Image Underst 1991; 53: 211-218.
- Chan TF, Vese LA. An active contour model without edges. Proc Scale Space Theor Comp Vis 1999; 141-151.
- Chan TF, Vese LA. Active contours without edges. IEEE Trans Image Process 2001; 10: 266-277.
- Wang XF, Huang DS, Xu H. An efficient local Chan-Vese model for image segmentation. Patt Recogn 2010; 43: 603-618.
- Li C, Kao CY, Gore JC, Ding Z. Implicit active contours driven by local binary fitting energy. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2007; 1-7.
- Li C, Kao CY, Gore JC, Ding Z. Minimization of region-scalable fitting energy for image segmentation. IEEE Trans Image Process 2008; 17: 1940-1949.
- Kaihua Z, Lei Z. Active contours with selective local or global segmentation: A new formulation and level set method. Imag Vis Comp 2010; 28: 668-676.
- Kaihua ZZ, Huihui S, Lei Z. Active contours driven by local image fitting energy. Patt Recogn 2010; 43: 1199-1206.
- Wang L, Li C, Sun Q, Xia D, Kao C. Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation. J Comp Med Imag Graphics 2009; 33: 520-531.
- Wang X, Huang D, Xu H. An efficient local Chan-Vese model for image segmentation. Patt Recogn 2010; 43: 603-618.
- Liu S, Peng Y. A local region-based Chan-Vese model for image segmentation. Patt Recogn 2012; 45: 2769-2779.
- Xiuming L, Dongsheng J, Yonghong S, Wensheng L. Segmentation of MR image using local and global region based geodesic model. Biomed Eng 2015; 14: 2769-2779.
- Zhang K, Zhang L, Lam KM, Zhang D. A level set approach to image segmentation with intensity inhomogeneity. IEEE Trans Cybern 2016; 46: 546-557.
- Kirsch R. Computer determination of the constituent structure of biological images. Comp Biomed Res 1971; 4: 315-328.
- Li C, Xu C. Distance regularized level set evolution and its application to image segmentation. IEEE Trans Image proc 2010; 19: 3243-3254.
- Marie-Pierre D, Anil KJ. A modified Hausdroff distance for object matching. Proceedings of the 12th International Conference on Pattern Recognition 1994; 566-568.