Research Article - Biomedical Research (2018) Artificial Intelligent Techniques for Bio Medical Signal Processing: Edition-II
An algorithm of parallel model checking programs with conditions based on adjustable predicate abstraction coding
Shaobin Huang, Dapeng Lang*, Ronghua Chi and Bai YuCollege of Computer Science and Technology, Harbin Engineering University, PR China
- *Corresponding Author:
- Dapeng Lang
College of Computer Science and Technology
Harbin Engineering University, PR China
Accepted on August 30, 2017
DOI: 10.4066/biomedicalresearch.29-17-700
Visit for more related articles at Biomedical ResearchAbstract
Introduction: Model checking is always considered as a logical analysis of a programme which evolves various challenges in the stages of verification. The abstraction model checking reduces the complexity of the process by translating the programme into a scale down version. Main challenge of model checking is that the space explosion may lead to a verification failure because of limited memory, timeout or space out. This giving-up result was never reported back before, which wouldn’t provide analysts much useful information about the system.
Aim: The process of abstraction coding has great relevancy in designing biological systems at molecular level. Development of abstraction hierarchies in biological engineering will help us further in categorizing the biological networks.
Materials and Methods: This paper combines several state-of-art model checkers, and adjusts predicate abstraction blocks dynamically during the verification of biological sequences. In this way when it comes to a verification failure, our algorithm will record and report an abstract version of path from the starting state to the current one. The reported paths could be used as an evidence for designers to review the programs.
Results and Conclusion: Our experiments show that based on the advantages of implementing different model checkers serially, we use message-passing to execute our algorithm to obtain a better performance. At last the parallel version of our methods outperform some of the popular algorithms as the system scale grows, which has wide applications in computer, biomedical and other disciplines.
Keywords
Model checking, Biological abstraction hierarchy, Parallel verification, Conditional verification.
Introduction
Synthetic biology is the new revolution in biological science where, biological entities are being redesigned based on engineering approaches such as abstraction, decoupling and standardization. Researchers have proposed various models of biological abstraction models such as using standard protocols like BioBricks, PoPS etc [1]. The recent researchers have developed prediction models based on the abstraction techniques. The examples are Lotka-Volterra Model, Molecular Prediction oscillator model etc.
As model checking has been widely used successfully in software verification. Researchers have focused on several basic areas in order to extend the application into industry scale in the last decade. The model checking and synthetic biology can revolutionize the sectors such as biosensors, biofuels, biomaterials and pharmaceutical industry [2-4].
When a nondeterministic input happens in a program that is being verified, a good chance is that because of the interleaving input the state space may increase dramatically, which is called state explosion. We use BDD as a symbolic model checking representation and apply CFA to handle parallel programs. This research is part of the study of ALGORITHM OF PARALLEL MODEL, which has wide applications in computer, biomedical and other disciplines [5].
Methods
Predicate abstraction is widely used by several model-checking tools like SLAM and C2BP. The core idea is to abstract a predicate set E in the program P into a Boolean program.
BP=(P,E)
in which P is the set of predicate over all the variables in the programs and E is the precision of predicate. Generally speaking, predicates in E are Boolean formulas of variables and constants in the programs. And in order to keep the branches in the programs, any path in P is also executable in the formula, which means they both have the same control structure. One predicate can be represented by a Boolean variable. Take a C program P is as follows. Based on P we have the corresponding set of predicates E: {s=s’, s=s’+2, s<8, x=2, y=3}
There are five predicates and in BP=(P,E) is the Boolean variable which represents the predicate (x==2). The value of a variable equals to that of a predicate. The non_def is a predicate with a random TRUE or FALSE value. And we also can obtain the Boolean program BP=(P,E).
We control the abstract process by controlling the size of abstract CFA edges that is we don't compute the predicate abstraction after every transition but on some certain circumstances. We use disjunctive path formula to store the strongest postcondition of the paths which are computed by IMAGEop(*). So there are two basic formulas an abstract state needs to satisfy, φ is an abstraction computation and ρ is a disjunctive path formula instead of a state formula which is the strongest postcondition right before the algorithm finishes computing the abstraction.
We borrow the concept CFA to represent a program flow.
Given a CFA edge 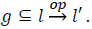
The IMAGEop operator computes the successors by extending
the path ρ or by adding a new abstraction ψ (ρ is a path
formula and ψ is a state formula, both of which are abstract
states). When reaching k states along the path we use
IMAGEop(φ) to compute a succeed state, in this part we define
a comb operator to merge k states before computing predicates.
Given a transition we compute merge two abstract states,
which are 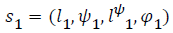 and
and 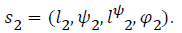 When it comes to combining the two states the method is
defined as follows: comb(s1,s2)=
When it comes to combining the two states the method is
defined as follows: comb(s1,s2)= 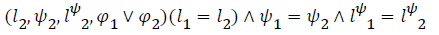 and s2 otherwise. The terminate state down below is the last
sink abstract state covering the other abstract states that are
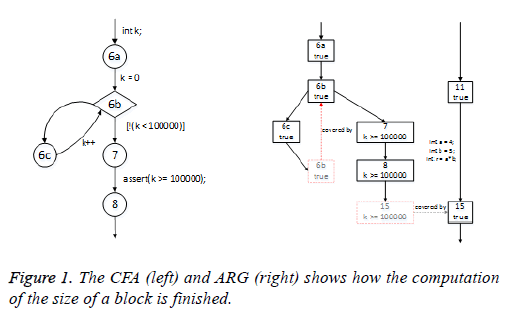
evaluated to TRUE along the path. The CFA and its ARG are
as Figure 1.
and s2 otherwise. The terminate state down below is the last
sink abstract state covering the other abstract states that are
evaluated to TRUE along the path. The CFA and its ARG are
as Figure 1.
Results
This paper restricts the performance comparison within three major techniques that are implemented in the same verification framework symbolically. The first technique is predicate abstraction which focuses on each single predicate in the program. And the second one is explicit abstraction which tracks every real number of variables. Table 1 shows that the new parallel algorithm outperforms BLAST and NuSMV by evidently less running time and furthermore has a more precise verification results. The precision rests on the difference that AMC has less incorrect verification results by introducing intermediate results [6-10].
| BLAST | SATABS | ||
|---|---|---|---|
| States | Times | States | Times |
| Apache 77 | 9802 | 113 | 5610 |
Table 1. Comparison with three tools.
Conclusion
A bottleneck of the framework that limits the further usage is its finite number of states along the abstract path, the state merging complexity when it comes to a start point of a loop. This is still a hot research area in the future. The scientists are looking synthetic and system biology as the new way through for industrial revolution. This is about to enable the devicelevel research in biology.
References
- http://www.openwetware.org/wiki/synthetic_biology:abstraction_hierarchy/network_layer_model
- Bryant RE. Graph-based algorithms for boolean function manipulation. IEEE Trans Computers 1986; 35: 677-691.
- Visser W, Mehlitz PC. Model checking programs with Java Pathfinder. In Proc SPIN 2005.
- Clarke EM, Grumberg O, Jha S, Lu Y, Veith H. Counterexample-guided abstraction refinement for symbolic model checking. J ACM 2003; 50: 752-794.
- Abdulla PA, Aronis S, Atig MF, Jonsson B, Leonardsson C, Sagonas K. Stateless model checking for TSO and PSO. Acta Informatica 2015.
- Beyer D, Henzinger TA, Keremoglu ME, Wendler P. Conditional model checking: A technique to pass information between verifiers. In Proc FSE ACM 2012.
- Beyer D, Henzinger TA, Th´eoduloz G. Program analysis with dynamic precision adjustment. In Proc ASE 2008.
- Clarke EM, Kroening D, Sharygina N, Yorav K. SATABS: SAT-based predicate abstraction for ANSI-C. In Proc TACAS 2005.
- Męski A, Penczek W, Rozenberg G. Model checking temporal properties of reaction systems. Informat Sci 2015; 313: 22-42.
- Mandrykin MU, Mutilin VS, Novikov EM, Khoroshilov AV, Shved PE. Using Linux device drivers for static verification tools benchmarking. Programming and Comp Softw 2012; 38: 245-256.