Research Article - Biomedical Research (2017) Volume 28, Issue 7
An adaptive unsupervised classification of seizure method based on LMDMSSE with EEG signals
Hao Ren1, Jianfeng Qu1*, Yi Chai1,2, Qiu Tang1 and Yuming Zhou1
1School of Automation, Chongqing University, Chongqing City, PR China
2State Key Laboratory of Power Transmission Equipment and System Security and New Technology, Chongqing University, Chongqing City, PR China
Accepted date: December 07, 2016
Abstract
On the basis of analyzing electroencephalogram (EEG) signals with nonlinear and nonstationary troubles, an adaptive unsupervised classification of seizure method, based on LMD-MSSE, is introduced into this article. The local mean decomposition (LMD), multi-scales sample entropy (MSSE) and the unsupervised classifier called K-nearest neighbors (KNN) are integrated in this method. Particularly, the LMD is utilized to obtain different component signals, adaptively, called product functions (PFs), and then using the MSSE to analyze these PFs to obtain sample entropies over different scales, which can describe the features of different status epileptics. In addition, KNN is employed to make full use of the typical morbid state features to detect the epilepsy. In order to show the superiority over this method, a series of epileptics are treated as an example and LMD-MSSE is employed to extract the features from EEG signals, and then the KNN classifier, Support Vector Machine (SVM) and Back Propagation Neural Network (BP) are all utilized to identify the different status epileptics. A comparison between the result obtained by this method and result adopted by previous studies with the same database (A-E) shows that the LMD-MSSE method has provided excellent performances in automatic seizure detection, which can be employed to realize the adaptive unsupervised epilepsy recognition.
Keywords
Electroencephalogram (EEG) signals, Local mean composition (LMD), Multi-scale sample entropy (MSSE), Automatic seizure detection.
Introduction
Epilepsy is one of the most common brain neurological diseases with 0.6-0.8% incidence of the world’s population [1], which can be characterized by the spontaneous and unforeseeable occurrence of seizures [2]. And furthermore, the EEG signals are always with nonlinear and nonstationary troubles. In recent years, driven by the demand of implementing fast automatic seizure detection, shortening the heal time, raising the success rate of the cure and protect the patients from accidents and save their life, classification of seizure theory and technology has thus become a research hotspot [2-7]. For many epilepsy patients, the major reasons are always developed with abnormal electrical function of brain cells, where the characterization parameters would change from multi-domains as time goes on [1,3-8]. As one of the world common disease, people with epilepsy always take antiepileptic drugs to control seizure and it always failed with 28 percent of them [2,9-12]. During seizure, the patient may lose his consciousness and fall down while walking or driving, which might cause a serious injury or become fatal [1-9,12]. Hence, the automatic seizure detection can be developed violently on the continuous recording of EEG with nonintrusive data acquisition. Currently, classification of seizures by visual inspection is very expensive and maybe inaccurate, and furthermore, the seizure is always episodic in their occurrences, so it is becoming more and more important to realize the adaptive automatic seizure detection, which can be used to realize the epilepsy detection device.
In automatic seizure detection, three steps are included, namely signals collection, feature extraction, and seizure recognition. EEG signals, collected with many noninvasive techniques, have primarily used in several epilepsy detection applications [2]. Due to the literature on extracting and selecting features from EEG signals are very abundant with several contributed proposals, and we just consider the data sets with non-invasive equipment. The feature extraction is the most important of three steps, which is always employed to distinguish the disease status. Moreover, accurate and efficient features can be easily obtained for automatic seizure detection so as to transform the linear and stationary signals into a series of complete and almost orthogonal components. However, the risen of the difficulty of extracting features of the complex EEG signals is always produced by the nonlinear and non-stationary troubles as well as interferences caused by external factors [1,3-8].
Thus, the traditional signal processing techniques with time and frequency domain may not be applied to detect the changes of EEG signals, effectively. Although there are a variety of analytical methods to analyze the EEG signals [2,9-12], but with the reason that the analysis and application of EEG signals in many situation require adaptive and unsupervised ability. And this directly led to the accuracy of evaluation about the working status of the brain systems has a low level of performance [13-16]. In order to improve the epilepsy feature extraction ability, several time frequency analysis methods, named short time Fourier transformation (STFT), Wigner Ville distribution (WVD), and the wavelet transform (WT), have been involved in a huge amount of literatures.
However, each of these methods has its limitations. The WT has been well employed in automatic seizure detection, but different mother wavelets would be predefined for each component. Moreover, WVD might cause cross-term interference in dealing with multi-component signals. Throughout these methods, it is easy to find out that they are all not self-adaptive, naturally. Recently, in order to explore the epilepsy mechanism, a lot of reporters had introduced the datadriven classification of seizure method. Besides, different types of measures are adopted so as to realize the adaptive automatic seizure detection, despite of which they generally investigate the definite seizure detection models or algorithms [13-16].
In recent decades, some self-adaptive decomposition techniques have been reported, two typical of which are empirical mode decomposition (EMD) and local mean decomposition (LMD). The method-EMD with superiority over self-adaptive signals processing was first introduced by Mosquera et al. [16] so as to solve the nonlinear and nonstationary problems. With the method of EMD, the signal can be decomposed into a series of complete and almost orthogonal components named intrinsic mode functions (IMFs). These IMFs describe the details and adumbrations of high-frequency to low-frequency; moreover, the appropriate method can be employed to extract the unexpected failure features. Besides, the corresponding method is LMD, proposed by Smith [17], which are suitable for transferring EEG signals into a series of PFs, adaptively. Although both have a lot of commons, LMD has better performance in local characteristic and time-scale of the signal, as well as the superiority to avoid being affected by undershoot or overshoot with fewer decomposed components and more reasonable physical information. With better features, better ability would be acquired to characterize the raw data. However, too many features would bring more complex calculations, which would thus to increase the time and space complexity.
In the study of following case, the limited of features extraction over EEG signal and the superiority over LMD in detail through the multi-scale sample entropy has been presented. On the basis of sample entropy, MSSE was proposed by Costa, which was originally used for heart rhythm variability research [18]. Compare with the approximate entropy and sample entropy, MSSE can analyze the series complexity under different scales. Besides, the computation of MSSE is simple. With all of these superiorities, MSSE would be facilitated to be more suitable for adaptive unsupervised classification of seizures. Therefore, LMD is employed to decompose the original signal into a series of PFs selfadaptively. After that, the MSSE is used to analyze the PFs to extract the effective epilepsy features. And then, these features can be utilized with all kinds of classifiers so as to realize the adaptive unsupervised classification of seizures. Furthermore, the implementation is also more complex. As one of the most famous and widely used unsupervised classification methods, the K-nearest neighbor (KNN) algorithm with its simplicity and effectiveness has been widely employed in large number of classification problems, such as medical diagnosis, handwritten recognition and satellite image scenes [19].
Our endeavors in this work are to develop a comprehensive evaluation on the confusion state of healthy or disease from the high frequency to low frequency. The classification of seizure method is not intended to substitute physicians, but rather to supply them an additional analyzing tool [2]. Therefore, the main targets and advantages of our system are:
• It can be used as an adaptive and unsupervised feature extraction method.
• And furthermore, this method can be used to realize the feature extraction on original signals from the high frequency to low frequency.
• After that, the MSSE can be employed to evaluate the differences in different statuses on the amount of information to evaluation the state of confusion of healthy or disease comprehensively, which can be fed into the classification machine.
In order to achieve these targets, the LMD is utilized to obtain different component signals, adaptively, called product functions (PFs), and then using the MSSE to analyze these PFs to obtain sample entropies over different scales, which can describe the features of different status epileptics. KNN is employed to make full use of the typical morbid state features to detect the epilepsy.
The paper is organized as follows: Section 2 introduces the methodology and the experimental materials. LMD has been employed to get product functions (PFs) and MSSE algorithm has been utilized to get features to classify and recognize the epilepsy, the principle of unsupervised classifier-KNN is also given. In Section 3, the experiment of EEG signals with LMDMSSE is studied, and multi-classifiers are utilized to distinguish the epilepsy. Besides, the result analysis and the performance of the proposed method of adaptive unsupervised automatic seizure detection are also presented. Follow by conclusions and future work, in Section 4.
Methodology and Materials
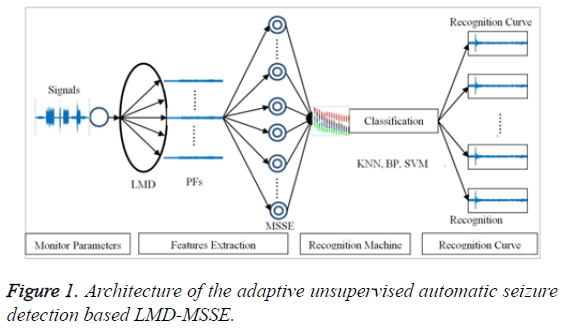
This paper, the model of unsupervised automatic seizure detection consists of epilepsy features extraction, classification machine and recognition curve, as shown in Figure 1. In terms of epilepsy features extraction, LMD is employed to transfer the original signal into PFs; moreover, MSSE is adopted to analyze the PFs to extract the effective epilepsy features. In this section, the principle of this method will be discussed.
LMD-MSSE algorithm and its epilepsy feature extraction
Given a signal x(t), appropriate methods are used to extract the typical epilepsy features, which can be fed into the classifier so as to realize the automatic epilepsy recognition, and have the requirements of being autonomous and unsupervised, etc. With the necessary of solving this problem, method called LMD algorithm is being introduced, with its working principle described as following steps:
(i) According to the signal x(t), all of the local extreme must be found out first, and then compute the mean of two successive maxima and minimum extreme, nij(k,1), k1=k1, k2, …, kM. Where kl refers to the index of the extreme. The subscript i denotes the number of PFs, and the subscript j represents the number of iteration to get a normalized frequency-modulated signal. The number of extreme is being described with M letter.
(ii).Calculate the local mean mij (t) and local magnitude aij (t), respectively.
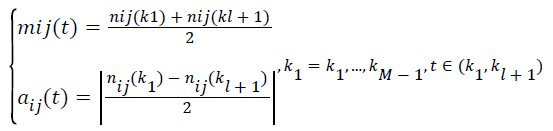 →(1)
→(1)
(iii) Connect all the local mean values mij(t) and magnitude aij(t) by straight lines, and smoothed with moving averaging (MA) to form a smoothly varying continuous function m?ij(t) and ãij(t).
(iv) Let
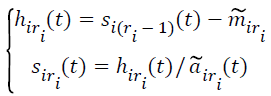 →(2)
→(2)
If siri(t) is a normalized frequency-modulated signal, then skip to the step (v). Otherwise, siri(t) as the original signal, return back to the step (i)-(iv), until siri(t) is a purely flat FM signal with the fluctuating between -1 and 1, where the subscript ri ≥ 2 denotes the number of iteration to compute the PF and s11 (t)=x(t).
(v) Calculate the relevant instantaneous amplitude (IA)ai(t), the instantaneous phase (IP)φi(t) and the instantaneous frequency (IF) fi(t) by the following functions. The sample rate is fs.
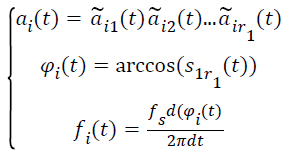 →(3)
→(3)
(vi) The PFs can be computed as follows according to envelope function and the final frequency demodulated signal.
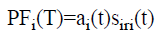 →(4)
→(4)
(vii) Compute the ui(t)=ui-1(t)-PFi(t), , which can be treated as the smoothed version of the original data, and repeated the steps (i)-(vi), until the ui(t) is a monatomic function or a constant, u0(t)=x(t). With regard to this point, the original signal can be decomposed into a series of PFs, and it can also be reconstructed according to the Equation (5).
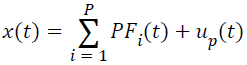 →(5)
→(5)
The entropy is always being used to measure the amount of information contained in a signal. With greater amount of information, there would be greater entropy. As a measure of uncertainty, when the probability of the occurrence of all events equaled, the value of entropy would be greater and the uncertainty would increase from the maximum. An event has a greater probability of the occurrence than any others, its entropy becomes smaller. While at the same time, the uncertainty would be smaller accordingly. For a random vector α, its entropy can be defined as
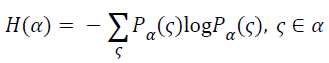 →(6)
→(6)
Where the Pα(ς) is the probability distribution of the random vector function.
As a new method to measure the complexity of limited time series data set, Multi-Scale Sample Entropy (MSSE) analysis can be employed in physical and physiology data sets. Moreover, this analysis method can be combined with some other entropy so as to solve the troubles over non-linear and non-stationary [20]. After analyzing the original signal by LMD method, the value of MSSE over different PF components varies, and which can reflect the complexity of the original signal at multi-scales. The process of MSSE algorithm can be described as follows:
(i).The sequence length can be described as M=int(N/τ), take the sequence to compose a m dimensional vector.
Y(σ)=[y(σ), y(σ+1),…,y(σ+m-1)], σ=1,2,…,M+m-1 →(9)
(ii) Calculate the distance between the vector Y(σii) and Y(σjj).
(iii) Give the similarity tolerance r, statistic the number of every d(σii, σjj) ≤ r (called template matching number), and the ratio of this number and total distance number, set as:
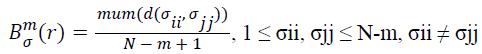 →(11)
→(11)
Calculate the mean of all σ:
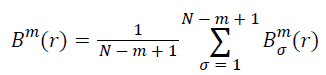
(iv) Take m+1 and repeat steps (i)-(iii), and then the Bm+1(r) can be obtained.
(v) Thus, the sample entropy estimation can be given as follows:
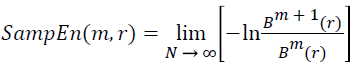 →(12)
→(12)
And when the width N is a limited specific value, the sample entropy of the width N signal can be obtained by:
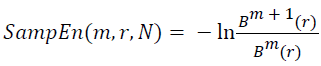 →(13)
→(13)
Employ the calculation of sample entropy and repeat the steps (ii)-(v) with the different scale factors τ. Therefore, the width N of original signals, scale factors τ, mode dimension m, and similarity tolerance r can be treated as the independent variable, while the sample entropy is being regarded as the dependent variable in an epilepsy features sequence, which can be expressed as MSSE(N, m, r, τ).
LMD-MSSE has provided with lots of superiority characteristics from the principle of this method. Physical means obtained by LMD-MSSE is clear. The ability measurement to produce a new model on the time series datasets, called entropy values, is thoughtful. Its calculation just needs a small data onto low time and space complexity. Only with a short data, can we get the robust sample entropy estimation, which is much better than correlation dimensions and Lyapunov exponent. Besides, good anti-noise and inference become another advantages. The LMD-MSSE can construct a new sequence of multi-dimensions of the original signal, due to which the original signal analysis becomes more systematic.
Recognition machine and its recognition curve
Through the LMD-MSSE method, different effective epilepsy features can be obtained. After that, different epilepsy features can be employed by classification machine so as to get the probability or the level of deviation from normal. However, in order to realize the real time of unsupervised automatic seizure detection, not only the accuracy needs to ensure, but also the time and space complexity need to lower.
Assume that there is a sample data set n1. Through the LMDMSSE, a sample entropy sequence shall be outputted under the scale factor τ, expressed as: SamEnχ=(E1,E2,…En1}, , and then identify a new data set n2 into the right class of the KNN method, it is being employed as follows:
(i) Select the sample data sets similar to the test data sets, which can be calculated by following function:
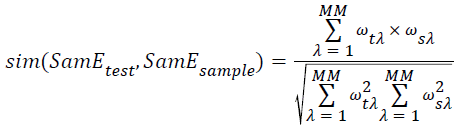 →(14)
→(14)
Where the SamEtest donates the feature vector, SamEsample donates the center vector of class Jsample, the MM donates the dimension of feature vector, ωλ indicates the λ dimension or neighbors of vector, and the parameter λ needs to be adjusted.
(ii).Calculate the weight of each class of the test of λ neighbors.
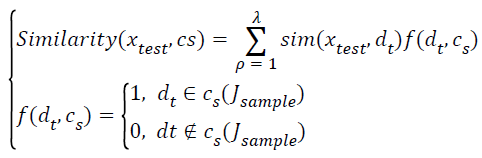 →(15)
→(15)
Where sim(xtest,dλ) denotes donates the similarity between the test data sets xtest and the nearest neighbor class Jsample.
(iii) Compare the class weights, and assigns the test data set into the largest category of weights.
The KNN classification, as the most well-known and widely used nonparametric pattern classification, is endowed with simplicity and effectiveness with the lazy-learning algorithm without training data set. Besides, the KNN is very suitable to realize the unsupervised automatic seizure detection with just O(n) time complexity and high accuracy. At this moment, the unsupervised seizure recognition machine can be summarized, as shown in Table 1.
| Input: | original signal x(t) with N width, scale factor τ, mode dimension m, similarity tolerance r, λ neighbors |
| Step1: | Employ the LMD algorithm to transfer the original EEG signals into a series of PFs. |
| Step2: | Measure the complexity of the PFs with Multi-Scale Sample Entropy (MSSE) analysis, and get the feature vector. |
| Step3: | Recognize the failure with failure feature vector by using the unsupervised KNN classification. |
| Step4: | The probability of various failure recognition curves is real-time exported. |
| Output: | The recognition Curve of various failures. |
Table 1: The adaptive unsupervised classification of seizure method.
Dataset
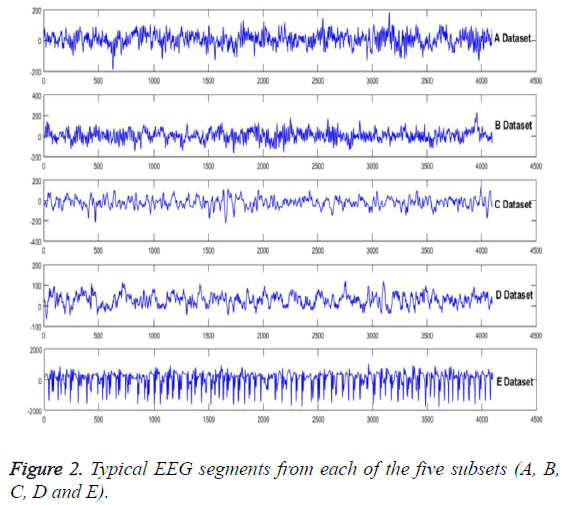
In order to show the superiority over the model, the experimental verification is taken on a public accessible EEG signals database [21]. The EEG signals, with strong nonlinear and non-stationary features due to the complicated working environments, are the typical example of the problem which can be solved by this method. Five subsets (A, B, C, D and E) of this database had been employed to compose the experiment dataset. Each one of the signals consists of 100 EEG signals with 4097 samples. Five healthy volunteers, with eyes open and closed, had been recorded the surface of EEG signals, include A and B dataset segments. Samples of C and D had been from the hippocampal formation of opposite hemisphere and epileptogenic zone of the brain, respectively. And for more, some activity measured during seizure free intervals between epileptogenic zones of the brain had been contained in C and D, respectively. The seizure activity just has been contained in E subset. Figure 2 is being employed to show the typical EEG signals.
Experiment and Discussion
The experiment of EEG signals with LMD-MSSE is studied, and multi-classifiers are utilized to distinguish the epilepsy. Besides, the result and the performance of the proposed method of adaptive unsupervised automatic seizure detection are also presented. A comparison between result obtained by this method and previous studies has been discussed to show the excellence of this method.
MSSE on the original data sets
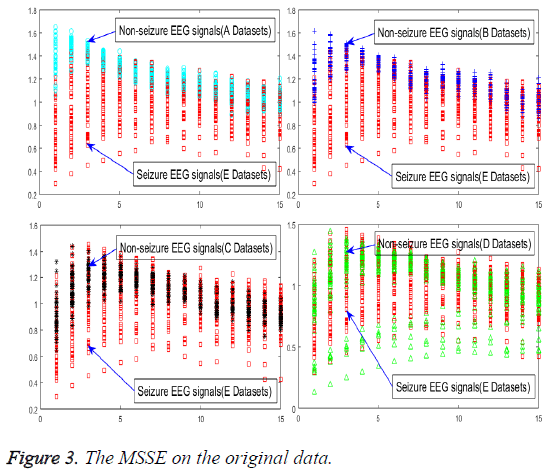
In order to achieve the unsupervised recognition of epilepsy, the impact on specialties of the original signal must be eliminated first, for which the features need to be extracted from the raw EEG signals, as shown in Figure 3.
An experiment of original signals, the MSSE of normal is greater than the other status. It means that when the probability of the occurrence of all events equaled, the value of entropy would be greater and the uncertainty would increase accordingly. An event has a greater probability of the occurrence than any others, its entropy becomes smaller, and the uncertainty would be smaller accordingly. Despite that all of these conclusions have appeared in this experiment, different status is endowed with the same MSSE, which cannot be used to realize the automatic seizure detection. However, the MSSE is quite different from different scales, which can be used as a guide to the selection of scale factor τ. It can reduce the time and space complexity violently with one or two factors τ to extract the effective epilepsy features.
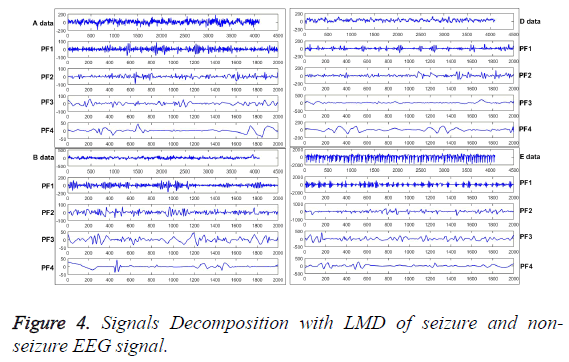
Signals decomposition with LMD
The PFs can be obtained from original signals by LMD applied, as shown in Figure 4, which are extracted from the typical seizure (A, B) and non-seizure (E, D) EEG signals, respectively. From the figures, the amplitude and the distribution curve of the frequency of high to low is quite different. And then, the entropy can be calculated with these obtained curves of EEG signal. In terms of epilepsy features extraction, LMD is employed to decompose original EEG signals to get the PFs first, then MSSE is adopted to analyze the PFs to extract the effective epilepsy features.
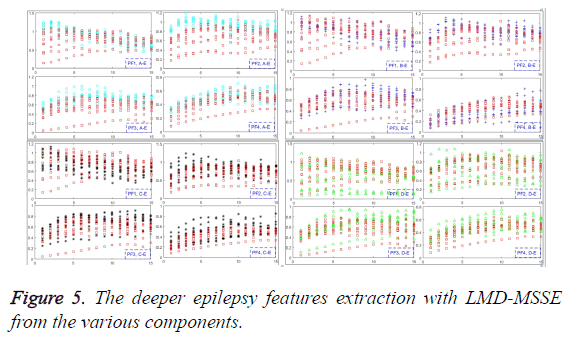
Various epilepsy components have been obtained, and each component of them reflects different characteristic components in the ideal situation. Furthermore, different disease statuses will produce different numbers of different components, which can be used to extract the deeper features by MSSE, as shown in Figure 5. From the Equation 5, original EEG signals have been decomposed into a series of PFs. Thus, the amount of information on original EEG signals is formed by each PF component. Then the MSSE can be used to analyze these PFs to obtain sample entropies over different scales, which can describe the features of different status epileptics.
Feature extraction with LMD-MSSE
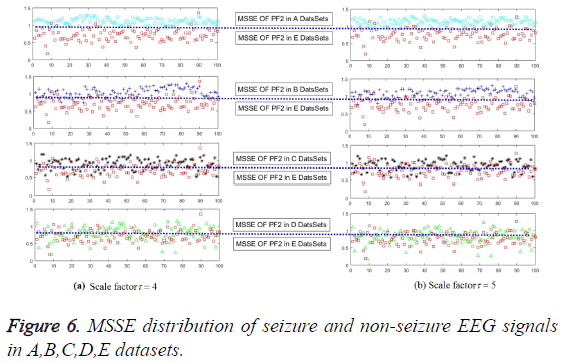
The direct and effective epilepsy feature extraction must meet the requirement to characterize different pathological status. The values of MSSE on PF1, PF2, PF3 and PF4 have been given in this section, as shown in Figure 5. Obviously, PF2 can satisfy the requirement, and for the PF1, PF3, PF4 are somewhat less good with all of the scale factors. It means that we can employ the multi-scale sample entropy of PF2 as the effective features of the epilepsy status. One more worthy to mention is that recognize the different failures with just several scale factors to get the features can greatly reduce the time and space complexity. Only in this way, great contributions can be made to realize the unsupervised effect.
The frequency of high to low on seizures and non-seizures is quite different. Information contained in high frequency is most of the noise part, and the useful part always contained in the frequency between the high and low. In this section, PF1 donates the high frequency, and PF2 implied the intermediate portion which can be used to reflect epilepsy features. PF3 and PF4 donate the low frequency which represents essential characteristics.
The adaptive unsupervised epilepsy recognition
In order to validate the excellence in the feature extraction method and to demonstrate the effect of the number of training samples, different percentages of samples are employed to train the model. In the first series of experiments, the scale factor is 4 or 5 on PF2 with 480 samples. Results have been shown in Figure 6 and the classification accuracy can be glanced at Table 3. The accuracy of epilepsy recognition rises violently with the increase in training data. As for the unsupervised KNN classifier, it is steadier than others. For this reason, it not only confirms previous theoretical analysis, but also quite consistent with previous reporters.
The average accuracies of prediction for different classification methods and different status are presented in Table 2. All parameters are the same as those in the last experiment. The Table 2 shows that the usual classification machine can recognize different statuses effectively, which means that the proposed method has an outstanding performance in epilepsy feature extraction with only several scale factors of PF2. When the number of scale factor increased, the average accuracies of the method would improve violently, as shown in Table 3.
| Classification Machine | Percentage of the samples used for training (A-E,AB-E,τ=4) | |||
|---|---|---|---|---|
| 10% | 18% | 40% | 80% | |
| SVM | 0.9553/0.9351 | 0.9859/0.9728 | 0.9908/0.9875 | 0.9965/0.9892 |
| BP neural | 0.8173/0.8940 | 0.9062/0.9587 | 0.9762/0.9885 | 0.9951/0.9987 |
| KNN | 0.9652/0.9956 | 0.9906/0.9972 | 0.9925/0.9780 | 0.9928/0.9789 |
Table 2: Average accuracies of the proposed method of different classifications in PF2.
| Classification machine | The scales used for feature extraction in LMD with A-E, AB-E (60% train samples) | |||
|---|---|---|---|---|
| PF2 (4) | PF2 (5) | PF2 (4,5) | PF2 (4,5,6) | |
| SVM | 0.9811/0.9899 | 0.9708/0.9596 | 0.9899/0.9899 | 0.9884/0.9884 |
| BP neural | 0.9876/0.9986 | 0.9755/0.9636 | 0.9967/0.9976 | 0.9976/0.9968 |
| KNN | 0.9926/0.9787 | 0.9719/0.9720 | 0.9900/0.9902 | 0.9907/0.9901 |
Table 3: Average accuracies of the proposed method of increasing scales to extract features.
To evaluate the excellence in the LMD-MSSE method of the adaptive unsupervised classification of seizures furthers, a valid comparison has been presented in Table 4. All these results have been tested with the method presented by these papers. Perhaps, these results have been represented somewhat difference with the original result, but it is really our experimental results. From the comparison, the LMD-MSSE proposed method achieves better results than others. Generally, LMD-MSSE method can supply a more suitable characterization in processing the EEG signals with non-linear and non-stationary troubles.
| Problem | Author | Methodology | Accuracy |
|---|---|---|---|
| A-E | Nigam et al. [22] | Nonlinear preprocessing filter, diagnostic artificial neural network | 97.2 |
| Subasi [23] | Discrete wavelet transform, mixture of expert model | 95 | |
| Guo et al. [24] | Discrete wavelet transform-relative wavelet energy, MLPNN | 95.2 | |
| Wang et al. [25] | Wavelet transform and Shannon entropy, kNN | 99.45 | |
| Nicolaou et al. [26] | Permutation entropy, SVM | 93.55 | |
| Fu et al. [27] | Time-frequency image using HHT, SVM | 99.12 | |
| Srinivasan et al. [28] | Time-frequency domain features, recurrent neural network | 99.6 | |
| Polat et al. [29] | FFT-decision tree classifier | 98.72 | |
| Fu et al. [1] | HMS analysis, SVM | 99.85 | |
| Tzallas et al. [9] | Time frequency analysis- artificial neural network. | 99.85 | |
| This method | LMD-MSSE feature extraction, KNN | 99.87 |
Table 4: A valid comparison of some previous studies.
Summary and Future Work
The achievement of this paper is to introduce an adaptive unsupervised automatic seizure detection method and illustrate its utility of the EEG signals. LMD can separate the EEG signals into a series of PFs, which contains feature information on original signals from the high frequency to low frequency. After that, the MSSE can be employed to evaluate the differences in different statuses on the amount of information, which can be fed into the classification machine.
With experiments, some interesting discoveries can be found out with the unsupervised automatic seizure detection, mainly including the following aspects:
• LMD and MSSE are successfully used to extract epilepsy features and then these features can be employed by a typical unsupervised machine to realize the automatic seizure detection unsupervised.
• A detailed comparison between LMD-MSSE and other works has been given. The result shows that LMD-MSSE is much better. The outstanding of LMD-MSSE mainly manifested in the epilepsy features vectors in different times, which can maintain a high degree of coincidence with different statuses.
• Represent signals in PF2 appear to be more suitable for combining MSSE on the feature extraction than any other PFs.
Through the LMD-MSSE method, different effective epilepsy features can be obtained with only several scale factors of PF2 on sample entropy. After that, different epilepsy features can be employed by classification machine so as to get the probability or the level of deviation from normal. However, the time and space complexity need to lower in order to realize the real-time of unsupervised automatic seizure detection, it will be researched in future work. From this work on EEG signals, LMD-MSSE can be used to provide lots of superiority characteristics with clear physical meaning. Only with a short data, can we get the robust sample entropy estimation, which is much better than correlation dimensions and Lyapunov exponent. Besides, good anti-noise and inference become another advantages. The LMD-MSSE can construct a new sequence of multi-dimensions of the original signal, due to which the original signal analysis becomes more systematic.
However, the work discussed in this paper is restricted to A, B, C, D and E datasets, which is a certain variation range. If EEG signals are remarkably changed, the accuracy and the efficiency of the proposed method would probably be affected. Consequently, further study can keep on the increasing adaptability the EEG signal in advance. In this study, the method is only applied to normal and epilepsy EEG signals, the future work should be done on different states of epilepsy to verify the generality or to find the problems or to make this proposed method to be more generalized. Furthermore, future work will focus on another direction with this method, which can be used to realize the classification of different seizure states during the seizure onset: pre-ictal (before the seizure onset), ictal (during the seizure onset), and post-ictal (after seizure).
References
- Fu K, Qu J. Hilbert marginal spectrum analysis for automatic seizure detection in EEG signals. Biomed Signal Process Control 2015; 16: 9-165.
- Subasi A. EEG Signal classification using wavelet feature extraction and a mixture of expert model. Expert Syst Appl 2007; 32: 1084-1093.
- Joshi V, Pachori RB, Vijesh A. Classification of ictal and seizure-free EEG signals using fractional linear prediction. Biomed Signal Process Control 2013; 9: 1-5.
- Li Y, Wei HL, Billings SA, Sarrigiannis PG. Time-varying model identification for time-frequency feature extraction from EEG data. J Neurosci Methods 2011; 196: 151-158.
- Bajaj V, Pachori RB. Automatic classification of sleep stages based on the time-frequency image of EEG signals. Comput Methods Programs Biomed 2013; 112: 320-328.
- Li S, Zhou W, Yuan Q, Geng S, Cai D. Feature extraction and recognition of ictal EEG using EMD and SVM. Comput Biol Med 2013; 43: 807-816.
- Alam SM, Bhuiyan MI. Detection of seizure and epilepsy using higher order statistics in the EMD domain. IEEE J Biomed Health Inform 2013; 17: 312-318.
- Zabihi M, Kiranyaz S, Rad AB, Katsaggelos AK, Gabbouj M. Analysis of High-Dimensional Phase Space via Poincaré Section for Patient-Specific Seizure Detection. IEEE Trans Neural Syst Rehabil Eng 2016; 24: 386-398.
- Tzallas AT, Tsipouras MG, Fotiadis DI. Epileptic seizure detection in EEGs using time-frequency analysis. IEEE Trans Inf Technol Biomed 2009; 13: 703-710.
- Li Y, Wei HL, Billings SA, Sarrigiannis PG. Time-varying model identification for time-frequency feature extraction from EEG data. J Neurosci Methods 2011; 196: 151-158.
- Liu H, Han M. A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings. Mechanism Machine Theory 2014; 75: 67-78.
- Li Y, Wee CY, Jie B, Peng Z, Shen D. Sparse multivariate autoregressive modeling for mild cognitive impairment classification. Neuroinformatics 2014; 12: 455-469.
- Pachori RB, Patidar S. Epileptic seizure classification in EEG signals using second-order difference plot of intrinsic mode functions. Comput Methods Programs Biomed 2014; 113: 494-502.
- Ocak H. Automatic detection of epileptic seizures in EEG using discrete wavelet transform and approximate entropy. Expert Syst Appl 36 2008; 36: 2027-2036.
- Tzallas AT, Tsipouras MG, Fotiadis DI. Automatic seizure detection based on time-frequency analysis and artificial neural networks. Comput Intell Neurosci 2007.
- Guerrero-Mosquera C, Trigueros AM, Franco JI, Navia-Vázquez A. New feature extraction approach for epileptic EEG signal detection using time-frequency distributions. Med Biol Eng Comput 2010; 48: 321-330.
- Smith JS. The local mean decomposition and its application to EEG perception data. J R Soc Interface 2005; 2: 443-454.
- Wang Y, He Z, Zi Y. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis. J Vib Acoust 2010.
- Fayed HA, Atiya AF. A novel template reduction approach for the K-nearest neighbor method. IEEE Trans Neural Netw 2009; 20: 890-896.
- Tiwari R, Gupta VK, Kankar PK. Bearing failure diagnosis based on multi-scale permutation entropy and adaptive neuro fuzzy classifier. J Vib Control 2015; 19: 461-467.
- Andrzejak RG, Lehnertz K, Mormann F, Rieke C, David P. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: dependence on recording region and brain state. Phys Rev E Stat Nonlin Soft Matter Phys 2001; 64: 061907.
- Nigam VP, Graupe D. A neural-network-based detection of epilepsy. Neurol Res 2004; 26: 55-60.
- Subasi A. EEG Signal classification using wavelet feature extraction and a mixture of expert model. Expert Syst Appl 2007; 32: 1084-1093.
- Guo L, Rivero D, Pazos A. Epileptic seizure detection using multi-wavelet transform based approximate entropy and artificial neural networks. J Neurosci Methods 2010; 173: 146-153.
- Wang D, Miao D, Xie C. Best basis-based wavelet packet entropy feature extraction and hierarchical EEG classification for epileptic detection. Expert Syst Appl 2011; 38: 14314–14320.
- Nicolaou N, Georgiou J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst Appl 2012; 39: 202-209.
- Fu K, Qu J, Chai Y. Classification of seizure based on the time-frequency image of EEG signals using HHT and SVM. Biomed Signal Process Control 2014; 12: 14-20.
- Srinivasan V, Eswaran C, Sriraam N. Artificial neural network based epileptic detection using time-domain and frequency-domain features. J Med Syst 2005; 29: 647-660.
- Polat K, Gunes S. Classification of epileptic form EEG using a hybrid system based on decision tree classifier and fast Fourier transform. Appl Math Comput 2007; 167: 1020-1024.