Research Article - Biomedical Research (2017) Volume 28, Issue 4
A study on discrete wavelet transform compression algorithm for medical images
Thirumoorthi C1* and Karthikeyan T21Assistant Professor, Hindusthan College of Arts & Science, Bharathiar University, Coimbatore, India
2Associate Professor, PSG College of Arts and Science, Coimbatore, India
- *Corresponding Author:
- Thirumoorthi C
Hindustan College of Arts and Science
Bharathiar University, India
Accepted on August 19, 2016
Abstract
Image compression is play vital role in medical area. In health field the bulk of medical image data produced every day is ever growing, mainly in grouping with the improved scanning resolutions and the importance of volumetric medical image data sets. In this work, six image compression methods are simulated. They are Karhunen-Loeve Transform (KLT), Walsh-Hadamard Transform (WHT), Fast Fourier Transform (FFT), Sparse Fast Fourier Transform (SFFT), Discrete Cosine Transform (DCT) and Discrete Wavelet Transform (DWT). The results of simulation are shown and compared different quality parameters of it are by applying on various lung cancer Computed Tomography (CT) scan medical images. The Discrete Wavelet Transform (DWT) method algorithm was given better results like Compression Ratio (CR), Structural Content (SC), Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR) compare to other transform methods. The Discrete Wavelet Transform (DWT) technique given improved result compared with other methods in all evaluation measures.
Keywords
Medical image, Image compression, Karhunen-Loeve transform, Walsh-hadamard transform (WHT), Fast fourier transform (FFT), Sparse fast fourier transform (SFFT), Discrete cosine transform (DCT), Discrete wavelet transform (DWT), Lung cancer computer tomography images, Compression ratio (CR), Structural content (SC), Mean square error (MSE), Peak signal to noise ratio (PSNR).
Abbreviations
KLT: Karhunen-Loeve Transform; WHT: Walsh-Hadamard Transform; FFT: Fast Fourier Transform; FT: Fourier Transform; SFFT: Sparse Fast Fourier Transform; DCT: Discrete Cosine Transform; DWT: Discrete Wavelet Transform; CT: Computed Tomography; CR: Compression Ratio; SC: Structural Content; MSE: Mean Square Error; PSNR: Peak Signal to Noise Ratio
Introduction
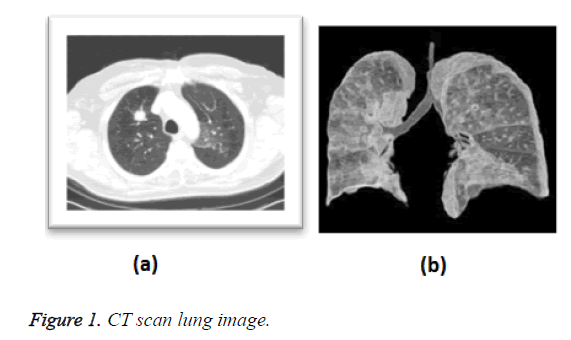
Medical science field and medical zone have large amount of medical images. So they need reduction the large volume amount of medical images. The medical Image compression is a process that focused on decreasing the size without losing quality, decrease the storage space of medical images and information of medical image. Lung cancer is the most common cause of cancer death in the world. Tobacco smoking cause’s etiology breath and lung cancer. Patients at highly effected by the lung cancer [1]. It could present with a variety of indications and is regularly screened by more common sicknesses. Several patients report no indications what so always, so it is vital that exact questions be enquired to try to produce info about symptoms they may not reflect abnormal [2]. In the case of an abnormal chest x-ray, the patient should directly undergo a chest CT scan for further evaluation. Figure 1 shows that the unusual lung CT’s inpatients who originally obtainable with weight loss and cough. The positron emission tomography was clarifying that the extent of the cancer [3]. When lung cancer is assumed, the patient stated to an oncologist, who will decide the supreme suitable diagnostic process (e.g., Bronchoscopy, CT guided lung biopsy, sputum cytology or media stinoscopy) and utmost favourable whole course of therapy for the lung cancer patient's specific needs [4].
Image Compression Methodology
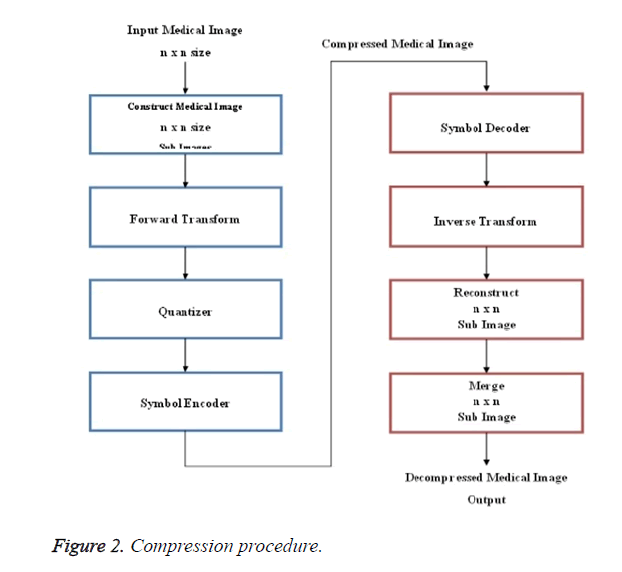
In this work to take different lung cancer CT scan image and using different image compression to compress image without loss. Walaa et al. [5] said the compression analysis results have indicated that the performance of the suggested method is much better, where the constructed medical images are less distorted and compressed with higher factor. The Image compression is process to remove the redundant information from the image so that only essential information can be stored to reduce the storage size, the transmission bandwidth and transmission time. Figure 2 shows that the essential information is extracted by various transforms techniques such that it can be reconstructed without losing quality and information of the image [6]. In this work comparative analysis of image compression is done by seven transform methods [7], which are Karhunen-Loeve Transform (KLT), Walsh- Hadamard Transform (WHT), Sparse Fast Fourier Transform (SFFT), Discrete Cosine Transform (DCT) and Discrete Wavelet Transform (DWT).
Karhunen-loeve transform (KLT)
Thus for any image KLT is the optimal information compaction transformation as well as for any number of retained coefficients. KLT basic functioning is dependent on image but, this however makes pre-computing impossible and hence this does not qualify it as a practical option suitable for image compression [7]. The KLT kernel is a unitary matrix, [V], whose columns, {uk} (arranged in descending order of eigenvalue amplitude), are used to transform each zero-meaned vector:
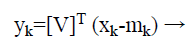 (1)
(1)
Walsh-hadamard transform (WHT)
Walsh system functions forms the very basis for Walsh transform. Walsh functions are orthogonal and have only +1 and -1 values [8]. In general, the Walsh transform can be generated by the hadamard matrix as follows:
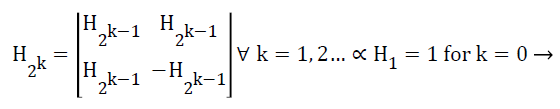 (2)
(2)
WHT here was employed to facilitate face as well as signature [9] recognition as WHT coefficients output array comprises only of integer values, resultantly hadamard transform thus becomes a quick transform, and implementation is feasible in O (N log N) additions as well as subtractions.
Fast fourier transform
Fourier transform is known to decompose image as two components: sinus and cosines. This implies that FT will transform any image from spatial to frequency domain respectively [10]. Fact is that any function can be precisely approximated using sum of infinite sinus and cosines functions [11]. The FFT is used to compute the Discrete Fourier Transform (DFT). The bigger size M=N × N matrix split into smaller size N’s of DFT in the time domain. The new radix-2 Decimation in Time (DIT) FFT is the effective and simplest method. It’s also used to compute 2n point DFT. In the FFT method the given weights are multiplied by indexes [5]. The output should be the bit reverse form of the given input signal. The compound conjugate regularity is used to signify the imaginary part. Fourier transform essentially is a method to execute this. Mathematically a two dimensional images Fourier transform in Equation 3.
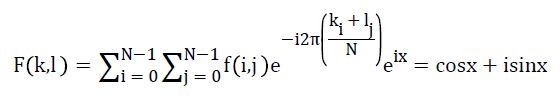 → (3)
→ (3)
Sparse fast fourier transform (SFFT)
SFFT computes k-sparse approximation, whose runtime depends upon k, the larger coefficient in the signal. This algorithm works in the process of identifying these k values by a filter G. ‘G’ concentrates in both time and frequency.
G is zero for all values except at a small number of time co-ordinates, and the Fourier transform of (�) is negligible except at a small fraction value which is about 1/k of the frequency co-ordinates. Gaussian or Dolph-Chebyshev function convolved with a box-car function is used to identify the large coefficients in sFFT [12]. Using this filter to find location and magnitude of the higher frequency component, parallel acceleration is achieved easily. Previous sub-linear algorithms have a runtime which is a polynomial in k and log n3. The fastest runtime of these algorithms will be calculated from Equation 4.
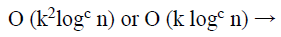 (4)
(4)
For some constants C>2.
The key feature of sFFT is its simple structure. It has an efficient runtime with low big-0th Constant. For a typical case of n which is a power of 2, the run time is calculated using Equation 5.
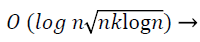 (5)
(5)
The implementation method and the working of sFFT with mathematical derivative.
Discrete cosine transform
The Discrete Cosine Transform (DCT) is an orthogonal transform, its attempts to de-correlate the medical image data. After the de-correlation each transform coefficient can be independently encoded without losing the compression efficiency [13]. The DCT transforms the signal from the spatial representation into the frequency representation. The DCT signify an image as a summation of sinusoids of the varying magnitudes and frequencies. DCT property is a typical image utmost of the visually substantial information about an image is focused in just few coefficients of DCT.
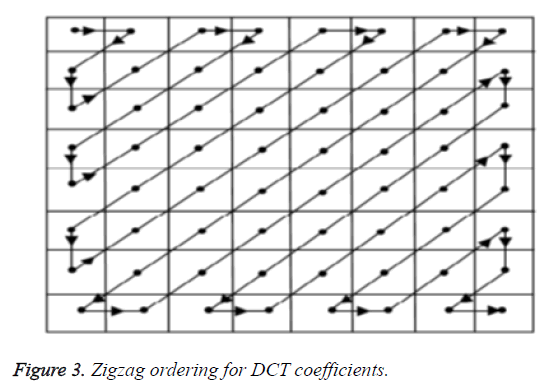
Afterwards the computation of the DCT coefficients, they are regularized according to a quantization table with the different measures provided by the JPEG image standard computed by the psycho visual evidence. The Selection of quantization table affects the compression ratio and entropy. The value of quantization is inversely proportional to quality of reconstructed image. Its gives better compression ratio and better mean square error [14]. In a quantization, the less significant frequencies are discarded, and then the maximum important frequencies that remain are used to recover the image in decomposition method. After quantization, the quantized coefficients are rearranged in the zigzag order for the further compressed by an effective lossy coding algorithm. DCT has several merits: (1). It has the ability to pack more information in least coefficients. (2). It decreases the block like appearance called the blocking artifact that outputs when margins between sub-images become visible [15].
An image is signified as the two dimensional matrix, the 2D DCT is used to compute a DCT coefficients of an image. The 2D DCT for an N × N input order can be defined with Equation 6.
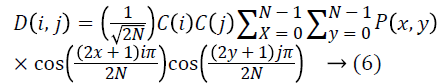 Where, P (x, y) is the input matrix image N × N, (x, y) are the coordinate of
the matrix elements and (i, j) are the coordinate of the coefficients, and C (u) is calculated using Equation 7.
Where, P (x, y) is the input matrix image N × N, (x, y) are the coordinate of
the matrix elements and (i, j) are the coordinate of the coefficients, and C (u) is calculated using Equation 7.
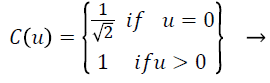 (7)
(7)
The reconstructed image is the computed by using the inverse DCT (IDCT) according to the Equation 8.
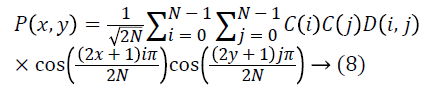
The black and white image pixels are ranged from 0 to 255, where 0 matches to pure black and 255 matches to a pure white. As DCT is constructed to work on pixel the values ranging from -128 to 127, the original block is the level off by 128 from every entry [16]. The step by step procedure of getting compressed image is using DCT and getting reconstructed image from the compressed image.
Currently encoding is completed and transmitted to receiver side in the form of the one dimensional array. This transmitted order saves in the text format. The array of compressed blocks that establish the image is stored in an extremely reduced amount of the space. Further the compression can be reached by applying suitable scaling factor [17]. In order to rebuild the output data, the rescaling and the de-quantization should be achieved as given in Equation 9.
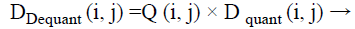 (9)
(9)
The de-quantized matrix is then transmuted back using the 2D inverse DCT. The equation for the 2D inversed DCT change is given in the above said Equation 10.
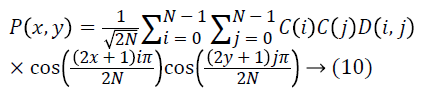
DCT separates images into the parts of different frequencies where less important frequencies are the discarded through quantization and important frequencies is used to retrieve to the image through decompression [8]. The following Equation 11 is given by the forward 2D-DCT transformation:
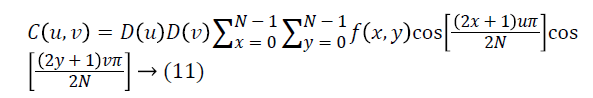
Where u, v=0, 1, 2, 3, …, N-1
The following Equation 12 is given by the inverse 2D-DCT transformation:
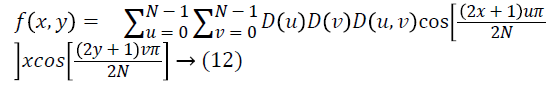
Where
D (u) = (1/N) ^ 1/2 for u=0
D (u) =2(/N) ^ 1/2 for u=1, 2, 3, ……., (N-1)
Compared to the other input dependent transforms, DCT have several advantages: (1) It have been implemented in single combined circuit; (2) It has the capability to pack most info in fewest coefficients; (3) It reduces the block like appearance so-called blocking artifact that results when limits between sub-images convert visible [18,19].
Discrete wavelet transform
The wavelet can be made from a scaling function which describes its scaling properties [20]. The limit that the scaling functions important be orthogonal to its discrete conversions implies some mathematical conditions on them which are mentioned ubiquitously, e.g. the dilation Equation 13.
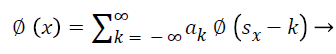 (13)
(13)
Here ‘S’ is a scaling factor. Furthermore, the area between the function essential be normalized and scaling function should be orthogonal to its integer translations, i.e. in Equation 14.
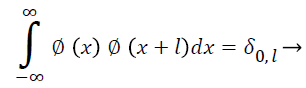 (14)
(14)
After presenting some more conditions (as the limitations above don’t produce a discrete solution) we can obtain results of all these calculations, the finite set of coefficients ak that describe the scaling function and similarly the wavelet [21]. The wavelet is got from the scaling function as N. Here ‘N’ is an even integer. The given set of wavelets then constructs an orthonormal basis which it uses to decompose the signal. The research is made with 128 × 128 medical image to compression and decompression with SFFT, DCT, DWT and calculating PSNR, MSE, CR, SC.
Performance Evaluation
Peak signal to noise ratio (PSNR in dB)
PSNR (Peak Signal-to-Noise Ratio) approximates image quality index, however on its own it does not have the capability of drawing a comparison between the features of two distinct images [22]. There is a possibility however that lower PSNR image may be considered as an image whose tone quality is comparatively better than one with a higher signal to noise ratio. PSNR can be calculated using Equation 15.
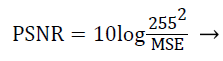 (15)
(15)
It refers to the relation between the power of the humiliating noise that affects the loyalty of its representation and the supreme imaginable power of the signal. As several signals inherently have an extensive dynamic range, PSNR generally is expressed as logarithmic decibel scale.
Mean square error (MSE)
It is a measure of image quality index. Large value of mean square basically implies that a poor quality image [23]. Mean square error called as MSE. Generally, it is a criterion that has been widely used and is representative of the classical error estimate as denoted by Equation 16.
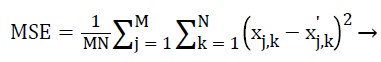 (16)
(16)
Where M and N are the image dimensions.
Compression ratio (CR)
Compression Ratio is the ratio of number bits required to represent the data before compression to the number of bits required to represent data after compression [24]. Increase of compression ratio causes more effective compression technique employed and vice versa. CR is calculated using Equation 17.
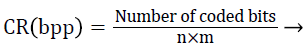 (17)
(17)
Structural content (SC)
Structural content measure that is employed to draw a comparison between two images inherent in several small image patches and to determine the images have in common [25]. A comparison is drawn between patches by deploying 2D continuous wavelet that acts as a low level corner detector. Large value of structural content SC basically implies a poor quality image. SC is calculated using Equation 18.
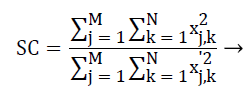 (18)
(18)
Experimental Results and Discussions
The experiment is carried out in MATLAB environment. In this research, the images deployed here for compression are all 128 × 128, 256 × 256 and 512 × 512 medical images. Basically meaning that images comprise of 128 × 128=16,384 pixels, 256 × 256=65536 pixels and 512 × 512=262144 pixels, wherein each pixel is represented by 8 bits or 1 byte. KLT, WHT, FFT, SFFT, DCT and DWT algorithm implementation has been carried out on MATLAB software and several different parameters have been ascertained with respect to the three medical images; comparison of reconstructed and original images PSNR, MSE, CR, SC values have been estimated.
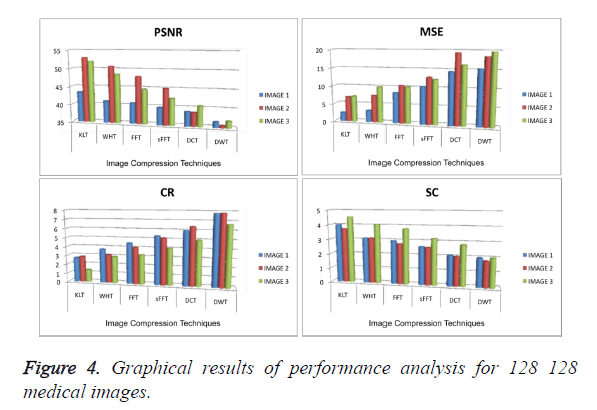
In Table 1, to take 128 × 128 size three CT medical images and simulated images using KLT, WHT, FFT, SFFT, DCT and proposed DWT compression techniques. In CT image 1 the proposed DWT compression produce better result in PSNR value is 36.9746 less than KLT, WHT, FFT, SFFT and DCT value is 43.3436, 41.0181, 40.7637, 39.7656 and 38.9746 respectively. In CT image 2 the proposed DWT compression produce better result in PSNR value is 36.874 less than KLT, WHT, FFT, SFFT and DCT value is 51.9335, 48.5279, 44.6743, 42.3932 and 40.6542 respectively. In CT image 3 the proposed DWT compression produce better result in PSNR value is 35.584 less than KLT, WHT, FFT, SFFT and DCT value is 52.8757, 50.6854, 47.9874, 45.0043 and 38.8023 respectively.
In CT image 1 the proposed DWT compression produce better result in MSE value is 15.342 higher than KLT, WHT, FFT, SFFT and DCT value is 2.342, 3.165, 8.437, 10.373 and 14.424 respectively. In CT image 2 the proposed DWT compression produce better result in MSE value is 19.653 higher than KLT, WHT, FFT, SFFT and DCT value is 7.0676, 9.9067, 10.0932, 12.3254 and 16.232 respectively. In CT image 3 the proposed DWT compression produce better result in MSE value is 19.313 higher than KLT, WHT, FFT, SFFT and DCT value is 6.874, 7.429, 10.453, 12.842 and 18.453 respectively.
In CT image 1 the proposed DWT compression produce better result in CR value is 7.7642 higher than KLT, WHT, FFT, SFFT and DCT value is 2.6822, 3.7365, 4.4844, 5.3433 and 5.9784 respectively. In CT image 2 the proposed DWT compression produce better result in CR value is 6.654 higher than KLT, WHT, FFT, SFFT and DCT value is 1.369, 2.9231, 3.242, 4.043 and 4.985 respectively. In CT image 3 the proposed DWT compression produce better result in CR value is 7.784 higher than KLT, WHT, FFT, SFFT and DCT value is 2.836, 3.1302, 4.043, 5.132 and 6.382 respectively.
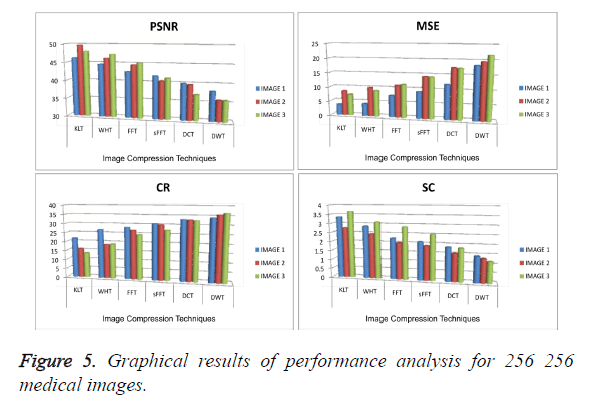
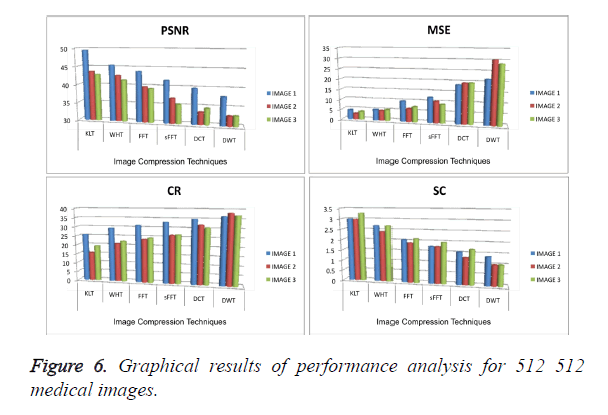
In CT image 1 the proposed DWT compression produce better result in SC value is 1.987 less than KLT, WHT, FFT, SFFT and DCT value is 3.984, 3.098, 2.965, 2.615 and 2.105 respectively. In CT image 2 the proposed DWT compression produce better result in SC value is 2.004 less than KLT, WHT, FFT, SFFT and DCT value is 4.534, 4.053, 3.785, 3.166 and 2.816 respectively. In CT image 3 the proposed DWT compression produce better result in SC value is 1.786 less than KLT, WHT, FFT, SFFT and DCT value is 3.723, 3.108, 2.768, 2.564 and 2.008 respectively. In order to 256 × 256 and 512 × 512 size of CT medical scan image also had the better performance for given proposed DWT method.
Figures 3-6 and Tables 1-3 explained the PSNR, MSE, CR and SC parameters performance evaluation of 128 × 128, 256 × 256 and 512 × 512 size respectively. The DWT method gave less SC value are given three CT image. Also it produced high MSE and CR value compare to the other exiting methods. It also shows in Figures 3-6.
| Medical image | Image compression technique used | PSNR | MSE | CR | SC |
|---|---|---|---|---|---|
| Image 1 | KLT | 43.3436 | 2.342 | 2.6822 | 3.984 |
| WHT | 41.0181 | 3.165 | 3.7365 | 3.098 | |
| FFT | 40.7637 | 8.437 | 4.4844 | 2.965 | |
| sFFT | 39.7656 | 10.373 | 5.3433 | 2.615 | |
| DCT | 38.9746 | 14.424 | 5.9784 | 2.105 | |
| DWT | 36.5643 | 15.342 | 7.7642 | 1.987 | |
| Image 2 | KLT | 51.9335 | 7.0676 | 1.369 | 4.534 |
| WHT | 48.5279 | 9.9067 | 2.9231 | 4.053 | |
| FFT | 44.6743 | 10.0932 | 3.242 | 3.785 | |
| sFFT | 42.3932 | 12.3254 | 4.043 | 3.166 | |
| DCT | 40.6542 | 16.232 | 4.985 | 2.816 | |
| DWT | 36.874 | 19.653 | 6.654 | 2.004 | |
| Image 3 | KLT | 52.8757 | 6.874 | 2.836 | 3.723 |
| WHT | 50.6854 | 7.429 | 3.1302 | 3.108 | |
| FFT | 47.9874 | 10.453 | 4.043 | 2.768 | |
| sFFT | 45.0043 | 12.842 | 5.132 | 2.564 | |
| DCT | 38.8023 | 18.453 | 6.382 | 2.008 | |
| DWT | 35.584 | 19.313 | 7.784 | 1.786 | |
| KLT: Karhunen-Loeve Transform; WHT: Walsh-Hadamard Transform; FFT: Fast Fourier Transform; FT: Fourier Transform; SFFT: Sparse Fast Fourier Transform; DCT: Discrete Cosine Transform; DWT: Discrete Wavelet Transform; CT: Computed Tomography; CR: Compression Ratio; SC: Structural Content; MSE: Mean Square Error; PSNR: Peak Signal to Noise Ratio | |||||
Table 1. Performance evaluation of various image compression techniques for 128 128 size medical image.
| Medical image | Image compression technique used | PSNR | MSE | CR | SC |
|---|---|---|---|---|---|
| Image 1 | KLT | 46.2234 | 3.659 | 21.6598 | 3.354 |
| WHT | 44.5483 | 4.243 | 26.7483 | 2.865 | |
| FFT | 42.6754 | 7.549 | 28.3232 | 2.245 | |
| sFFT | 41.7685 | 9.085 | 30.5442 | 2.098 | |
| DCT | 39.9867 | 11.875 | 32.9322 | 1.856 | |
| DWT | 38.0933 | 18.386 | 34.0985 | 1.4325 | |
| Image 2 | KLT | 49.6754 | 8.6087 | 15.8769 | 2.764 |
| WHT | 46.2376 | 9.9435 | 18.6741 | 2.456 | |
| FFT | 44.5643 | 11.0874 | 26.7834 | 2.006 | |
| sFFT | 40.4524 | 14.3453 | 29.9454 | 1.893 | |
| DCT | 39.6654 | 17.4342 | 32.8948 | 1.534 | |
| DWT | 35.784 | 19.6504 | 35.656 | 1.324 | |
| Image 3 | KLT | 48.054 | 7.3453 | 13.543 | 3.654 |
| WHT | 47.283 | 9.0273 | 18.954 | 3.104 | |
| FFT | 45.132 | 11.3776 | 24.543 | 2.875 | |
| sFFT | 41.242 | 14.242 | 27.23 | 2.505 | |
| DCT | 37.0398 | 17.3453 | 32.532 | 1.813 | |
| DWT | 35.765 | 21.6435 | 36.532 | 1.165 | |
| KLT: Karhunen-Loeve Transform; WHT: Walsh-Hadamard Transform; FFT: Fast Fourier Transform; FT: Fourier Transform; SFFT: Sparse Fast Fourier Transform; DCT: Discrete Cosine Transform; DWT: Discrete Wavelet Transform; CT: Computed Tomography; CR: Compression Ratio; SC: Structural Content; MSE: Mean Square Error; PSNR: Peak Signal to Noise Ratio | |||||
Table 2. Performance evaluation of various image compression techniques for 256 256 size medical image.
| Medical image | Image compression technique used | PSNR | MSE | CR | SC |
|---|---|---|---|---|---|
| Image 1 | KLT | 49.3488 | 4.4732 | 25.546 | 2.985 |
| WHT | 45.4341 | 5.1613 | 29.337 | 2.687 | |
| FFT | 43.8734 | 9.8453 | 31.1216 | 2.045 | |
| sFFT | 41.6484 | 12.1232 | 33.0082 | 1.767 | |
| DCT | 39.7563 | 18.4633 | 34.6578 | 1.546 | |
| DWT | 37.763 | 21.3412 | 36.425 | 1.365 | |
| Image 2 | KLT | 43.6357 | 2.8152 | 15.5156 | 2.964 |
| WHT | 42.6754 | 4.8243 | 20.9442 | 2.404 | |
| FFT | 39.7542 | 6.2434 | 23.5433 | 1.897 | |
| sFFT | 36.9232 | 10.3433 | 26.2353 | 1.761 | |
| DCT | 33.4599 | 19.315 | 31.8172 | 1.286 | |
| DWT | 32.764 | 30.123 | 38.124 | 1.004 | |
| Image 3 | KLT | 42.874 | 3.986 | 19.4232 | 3.267 |
| WHT | 41.453 | 5.343 | 22.342 | 2.682 | |
| FFT | 39.354 | 7.342 | 24.345 | 2.103 | |
| sFFT | 35.343 | 9.0345 | 26.432 | 1.973 | |
| DCT | 34.547 | 19.453 | 30.5422 | 1.675 | |
| DWT | 32.843 | 28.4126 | 36.8724 | 1.008 | |
| KLT: Karhunen-Loeve Transform; WHT: Walsh-Hadamard Transform; FFT: Fast Fourier Transform; FT: Fourier Transform; SFFT: Sparse Fast Fourier Transform; DCT: Discrete Cosine Transform; DWT: Discrete Wavelet Transform; CT: Computed Tomography; CR: Compression Ratio; SC: Structural Content; MSE: Mean Square Error; PSNR: Peak Signal to Noise Ratio | |||||
Table 3. Performance evaluation of various image compression techniques for 512 512 size medical image.
Conclusion
This work is concentrated on the comparison among six main KLT, WHT, FFT, SFFT, DCT and DWT methods of image compression. In this paper analysis of various Image compression approaches for different images is done based on parameters, Mean Square Error (MSE), Compression Ratio (CR) and Peak Signal to Noise Ratio (PSNR). The comparison of KLT, WHT, FFT, SFFT, DCT and DWT after compression the parameters like PSNR values, MSE, CR and SC values were good outcome in proposed DWT work. From the above study it can be seen that proposed DWT take less PSNR value and SC value than KLT, WHT, FFT, SFFT and DCT. The proposed method has more compression ratio and MSE value than KLT, WHT, FFT, SFFT and DCT. Our simulation results from result and discussion chapter shows that we can achieve higher compression ratio using DWT compression technique. DWT transform gives higher compression ratio but for getting that clarity of the image is partially trade off. It is more suitable for regular applications as it is having a good compression ratio along with preserving most of the information. Further research work can be performed to relax high compression ratio constraint and transform. This work has been concentrate transform image using for the elimination of the spatial redundancy by different compression of medical images.
References
- Fukuoka M, Yano S, Giaccone G, Tamura T, Nakagawa K. Multi-institutional randomized phase II trial of gefitinib for previously treated patients with advanced non-small-cell lung cancer. J Clin Oncol 2003; 21: 2237-2246.
- Pre-treatment evaluation of non-small-cell lung cancer. The American Thoracic Society and The European Respiratory Society. Am J Respir Crit Care Med 1997; 156: 320-332.
- Halpern MT, Gillespie BW, Warner KE. Patterns of absolute risk of lung cancer mortality in former smokers. J Natl Cancer Inst 1993; 85: 457-464.
- Mohammed AA, Hussein JA. Hybrid transform coding scheme for medical image application. IEEE Isspit 2010; 10: 237-240.
- Walaa M, Abd E, Wajeb G. Color image compression algorithm based on DCT blocks. Int J Comp Sci Issue 2012; 9: 323-328.
- Zhang SQ, Zhang SF, Wang XN, Wang Y. The image compression method based on adaptive segment and adaptive quantified. IEEE Icicic 2008; 8: 353-353.
- Xie Y, Jing X, Sun S, Hong L. A fast and low complicated image compression algorithm for predictor of JPEG-LS. IEEE IC NIDC 2009; 353-356.
- Al-Fayadh A, Hussain AJ, Lisboa P, Al-Jumeily D. An adaptive hybrid classified vector quantisation and its application to image compression. IEEE Comp Model Simul 2008; 253-256.
- Roy AB, Dey D, Mohanty B and Banerjee D. Comparison of FFT, DCT, DWT, WHT compression techniques on electro cardiogram and photo plethysmography signals. Int J Comp Appl 2012; 975-888.
- Thirumoorthi C, Karthikeyan T. A review on embedded zero wavelet transform coding. Proc Nat Adv Trends Inf Technol 2012; 40.
- Mridul KM, Gunjan M. Image compression using DFT through fast Fourier transform technique. Int J Emerg Trends Technol Comp Sci 2012; 1.
- Karthikeyan T, Thirumoorthi C. Easy optimization of image transformation using sFFT algorithm with HALIDE language. Int Conf Contemp Comp Inform 2014; 1188-1190.
- Singh H, Sharma S. Hybrid image compression using DWT, DCT and Huffman encoding techniques. Int J Emerg Technol Adv Eng 2012; 2: 300-306.
- Anoop M, Bensiker RSD. Image compression using lifting based DWT. Int J comp Inf Technol Eng 2009.
- Elharar E, Adrian S, Ofer H. A hybrid compression method for integral images using discrete wavelet transform and discrete cosine transform. J Display Technol 2007; 3: 321-325.
- Sriram B, Thiyagarajans S. Hybrid transformation technique for image compression. J Theor Appl Inf Technol 2012; 4.
- Harjeet PS, Sakhi S. Hybrid image compression using DWT, DCT and Huffman encoding techniques. Int J Emerg Technol Adv Eng 2012; 2.
- Shrestha S, Wahid K. Hybrid DWT-DCT algorithm for biomedical image and video compression applications. IEEE ICISSPA 2010; 280-283.
- Roy AB, Dey D, Mohanty B, Banerjee D. Comparison of FFT, DCT, DWT, WHT compression techniques on electrocardiogram and photoplethysmography signals. IJCA International Conf Comp Comm Sens Netw 2012; 6-11.
- Singh S, Kumar V, Verma HK. DWT-DCT hybrid scheme for medical image compression. J Med Eng Technol 2007; 31: 109-122.
- Karthikeyan T, Thirumoorthi C. Embedded Zero Tree Wavelet (EZW) algorithm based image transformation for easy optimization with HALIDE language. Int J Appl Eng Res 2015; 10: 1551-1554.
- Karthikeyan T, Thirumoorthi C. A survey on embedded zero tree wavelet. Int J Comp Sci 2014; 2: 353-357.
- Singh S, Kumar V, Verma HK. Adaptive threshold-based block classification in medical image compression for teleradiology. Compute Biol Med 2007; 37: 811-819.
- Chuanwei S, Quanbin L, Jingao L. The study of digital image compression based on wavelets. ICALIP 2010.
- Anoop M, Bensiker RSD. image compression using lifting based DWT. Int J comp Inf Technol Eng 2009.