Research Article - Biomedical Research (2016) Volume 27, Issue 4
A prediction method using instantaneous mixing plus auto regressive approach in frequency domain for separating speech signals by short time fourier transform
C Anna Palagan1* and K Parimala Geetha2
1Department of ECE, Rajas Engineering College, Vadakkangulam, Tirunelveli, Tamilnadu, India
2Department of ECE, Ponjesly College of Engineering, Nagercoil, Tamilnadu, India
Accepted on April 14, 2016
Abstract
The revealed works of separation of speech signals, the most disadvantages is that the incidences of distortion speech at intervals the signal that affects separated signal with loud musical noise. The thought for speech separation in normal Blind Source Separation (BSS) ways in which is solely one sound supply in an exceedingly single area. The projected methodology uses as a network that has the parameters of the Instantaneous Mixing Auto Regressive model (IMAR) for the separation matrices over the entire frequency vary. A trial has been created to estimate the simplest values of the Instantaneous Mixing Auto Regressive model (IMAR) model parameters using two matrices W and G by suggests that of the maximum-likelihood estimation methodology. Supported the values of those parameters, the supply spectral half vectors square measure calculable. The whole set of Texas Instruments Massachusetts Institute of Technology (TIMIT) corpus is utilized for speech materials in evolution results. The Signal to Interference quantitative relation (SIR) improves by a median of 5dB unit of measurement over a frequency domain BSS approach.
Keywords
Blind source separation, Separation matrices, Instantaneous mixing plus auto regressive (IMAR) model, Maximum likelihood estimation.
Introduction
The audio and speech signal process applications, the separation of speech signals is extremely vital done by exploitation Blind supply Separation (BSS) technique. The BSS has been employed in multi verbalize applications and acoustics signal process. Many adaptation step size strategies for BSS for automaton audition systems [1] are planned. The parameters aren't adjusted manually and there's no want of further preprocessing. For the moving sources [2] the positions and velocities of the supply is obtained from the 3D hunter supported Markov chain town particle filter which ends up in high rottenness. During this methodology it provides separation of the sources with none previous data of moving sources and its accustomed perform real time speech sweetening. In frequency domain, the permutation issues [3] a brand new technique that partitioned off the complete frequency bands into little regions by exploitation correlation of separate signal powers. The region wise permutation alignment is performed by region growing manner. Here the permutation alignment relies on lay to rest frequency dependence of separated power signal.
For multi-channel acoustic echo cancelation [4] the ICA is conjointly perform supply separation and multichannel acoustic cancellation through semi BSS while not double track detection. To cut back the result of non-singularity the matrix constraint is employed. For police investigation a time varied intermixture matrix the short time Fourier rework [5] is employed. In frequency domain [3,6] for reducing the process quality and increase the speed frequency domain BSS is employed. During this algorithmic rule the upper order frequency dependencies those using real room recordings. For extracting freelance from array signals the metallic element unvaried algorithmic rule [7] is employed. For finding the nonunitary joint resolution drawback in BSS a coinciding Biunvaried algorithmic rule is introduced. Within the multiple sources case, so as to seek out the correct estimation of propagation time delays [8] Generalized State Coherence rework (GSCT) that is a non-linear rework of the house drawn by the complete demixing matrices. In biconvex divergence ICA algorithmic rule, [9] the supply signals of the blind sources springs by the characteristics of Parzen window based mostly distribution. Supported the experimental results this algorithmic rule is that the quick algorithmic rule for the blind sources that involves speech and music signals. For cancelling the echo’s within the blind sources throughout continuous double track [10] so as to estimate the blind supply signals the most chance approach is employed.
In the last decade Blind Source Separation (BSS) methods have been widely used in the field of biomedical engineering. Noise reduction and useful signal extraction are among the most significant applications of BSS [11]. More particularly, assume that one realization of N-dimensional random vector process {x[m]m∈N} with values in the real field is available. The simulated sources are denoted by EEGS, EOGRS, EOGLS and ECGS. They represent brain activity, rapid eye movements, slow eye movements and cardiac activity, respectively. More precisely, the EEGS source is simulated using the model of Jansen where parameters were selected to derive a cerebral background activity. Note that the statistical distribution of this signal is quasi-Gaussian. This is in agreement with real background EEG data. The other sources are derived from our sleep recordings database presented in. More precisely, the EOGRS source is issued from a band-pass filtering (between 1 Hz and 8 Hz]) of the derivation FPZ-CZ of the standard 10-20 system. The EOGLS source corresponds to a low-pass filtering of the classical derivation E1-E2 with the cut-off frequency of 4HZ in order to reduce the effect of EEG and EMG interference. Finally, the ECGS source corresponds to a cardiac signal recorded on patients during their sleep. In reference to the additive noise {v[m]m∈N}, it is modeled as a spatially correlated Gaussian noise with the spatial correlation equal to 0.5. An example of 20 seconds portion of original sources, observations and estimated sources.
Generation of the mixing matrix
To derive the mixing matrix associated with the brain and ocular activities, a three concentric sphere head model is used. Four dipoles located at four fronto-parietal positions and a patch of two hundred dipoles (uniformly located in the cortex) characterize the eye movements (rapid and slow) and the background EEG sources, respectively. The EEG recording system contains four electrodes plus one reference electrode: two temporal sensors, in front of the higher part of the ears, denoted by F7m and F8m (where m stands for modified), two frontal sensors, above the eyes, denoted by FP1m and FP2m, and the reference electrode CZ located at the top of the head. Then the transfer formula describing the relationship between current dipoles and surface observation is used to obtain the (4 × 3) mixing matrix A′. Since the heart contribution to the data is assumed to be non-uniform on all the channels, we decide to add to the (4 × 3) mixing matrix A′ a fourth column vector a4 with different components. Note that the obtained mixing matrix A=[A′a4] is slightly ill-conditioned.
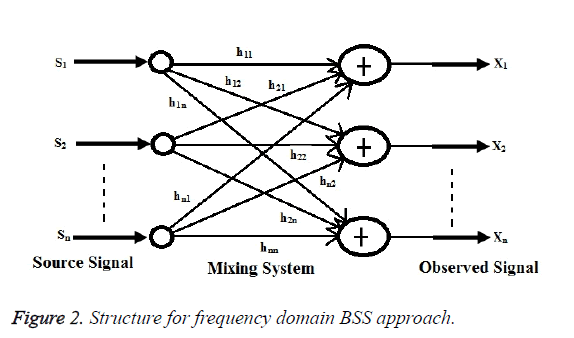
Blind Source Separation (BSS) ways aim to realize this goal supported some previous data of the supply signal properties. Following the physics of sound intermixture, allow us to take into account N sources sm(t), m=1,…,N to be convolutively mixed. At M sensors, the recorded mixture signals ai(t), i=1, …,M is denoted by
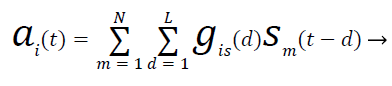 (1)
(1)
Where L is that the delay length on the order of 103-104 taps (each regulator last 1/Fs second where ever Fs is that the sampling frequency) in AN passing commonplace space gis(d) is that the separate Green’s perform of the world, collectively referred to as the world impulse response (RIR). The (severely ill-posed) mathematical downside is to recover every Gis(d) and sm(t) from Ai(t). A significant branch of BSS is that the therefore mentioned as freelance component analysis (ICA) that assumes that the availability signals unit orthogonal to (or freelance of) each other [12]. ICA could be an additional general methodology than ill sound signals. The time domain ICA [13,14] makes an attempt to estimate the gis directly so as to contend with a high dimensional non convex optimization downside [12,15]. Frequency domain ICA [16-18] solves AN fast (L=0) version of (1) in every frequency bin once applying the Discrete Fourier Transform (DFT) to (2) frame by frame:
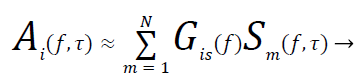 (2)
(2)
Where (Ai, Gis & Sm) unit the T-point DFT of (ai, gis & Sm) severally, and τ is that the frame selection. The larger T/l unit, the upper the approximation. Attributable to the absence of the regularity in d of gis and sm, DFT does not retread convolution to native product exactly. The frequency domain approach is restricted to use an extended DFT. additionally to computations to delineated scaling and permutation ambiguities once synthesizing multi-frequency estimation of Sm(f,τ) back to a time domain output [12,15]. Imperfections and errors in scaling and permutation within the frequency domain might result in artifacts within the time domain signals at the ultimate output.
Existing Methods and New Idea
BSS refers to the drawback of the signals from many discovered linear mixtures. Up to currently, finding the BSS drawback in associate underdetermined case has principally consisted in assumptive that the speech signals was sufficiently thin [19-22]. However, due to surprising discontinuous zeropadding, such separated signals have sizable distortion, and thus a loud musical noise is detected. In [21], associate calculable admixture matrix was used for finding the determined BSS drawback. Our suggestion for eliminating the distortion matter is to mix scantiness with admixture matrix estimation. So we are able to acquire additional info regarding the signals to be separated and to cut back the zero-artefact result, from that the musical noise originates. Whereas Vielva et al., Rickard associated Yilmaz worked on an undetermined fast case using scantiness [19-21], and Deville on a determined fast case utilizing a admixture matrix estimation [21], here, we tend to area unit managing undetermined BSS in a very convolutively case.
Blind source separation of speech and music signals
Blind Source Separation (BSS) may well be a technology for separating mixtures of multiple speech signals. This technology has been studied extensively and important progresses square measure transformed the last decade. However, typical BSS ways in which performs very poor once the reverberation time is huge. Several researchers have selfaddressed this drawback, but it's still associate open question. Our approach to overcoming this limitation is to unify BSS and performing arts BSS can notice BSS even underneath extremely live environments.
Figure 1 is an example for speech separation of an interior area downside. For these applications, the moment combination model might even be applicable as a result of the propagation delays is negligible. However, in real environments substantial time-delays might occur Associate in an exceedingly style and formula is needed to account for the mixing of time-delayed sources and convolved sources. It focuses on the implementation of the educational rule and on problems that arise once separating speakers in space recordings. It used associate informal approach throughout a feed forward network enforced among the frequency domain pattern the polynomial filter pure mathematics technique. Below minimum-phase combine conditions this preprocessing step was adequate for the separation of signals. These methods successfully separated a recorded voice with music among the background (indoor area problem).
Proposed Method
Imar model to generate microphone signals
In the planned methodology the BSS is recovered of supply signals by LTI filter and permutation. The time domain Blind source Separation approach is employed here. During this planned methodology the estimation of blind source signal is within the variety of source signal vector baccalaureate (n) by applying Associate in Nursing IM input signals and IS output separation filter price to discovered signal vector O (n). Within the time domain BSS approach for separating sound mixtures the order of the separation filter is about a price that exceeds the space reverberation time. The order of the separation filter becomes terribly massive for the reverberation time is long. That the convergence rate is poor and therefore the price for computation is extremely high. The estimation of supply spectral part vector within the frequency domain BSS approach is completed by applying a separation matrix to the discovered spectral part vector.
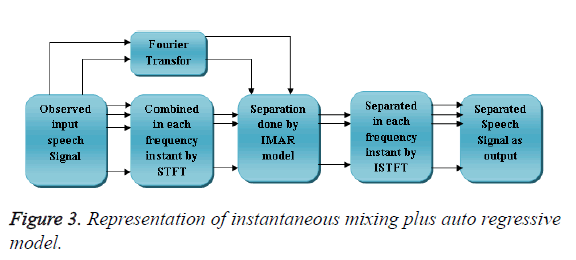
During this planned methodology the assessment may be a multiple sound supply case, wherever IM=2. During this thought the frequency domain BSS approach as shown in Figure 2. A pair of is by exploitation WPE methodology as a preprocessor that illustrate the case of IS=IM=2. As a result of within the start we have a tendency to use prediction error with 1st electro-acoustic transducer for BSS method. Figure 3 shows the structure for commixture of speech signals.
For any microphone as the prediction target as
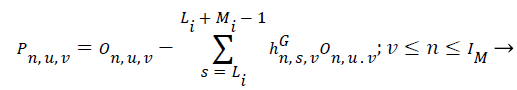 (3)
(3)
Where {hn,s,v} Li ≤ Li+Mi-1 denoted the prediction filter for the Ith electro-acoustic transducer spectral part and Pn,u,v is that the corresponding prediction error. The various spectral part outputs P1,u,1…..PIm,u,1 is obtained. The fast mixtures of the supply spectra elements were thought of for these elements. supported the speculation of Multichannel linear prediction the values of P1,u,1,……PIm,u,1 become nearly fast mixtures by mistreatment applicable prediction filters though such prediction filters might not be able to obtained with the WPE technique. For the mth electro-acoustic transducer the prediction filter values area unit Dn,s,v.
It's assumed that the bin indices is one for all frequencies from the set of exists values of X1 and L1 ≤ L1+M1-1 that is equalize the output spectral part vector Bu,1 supported these assumptions we have a tendency to known Zu,1 with Bu,1 is
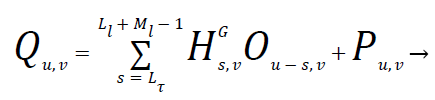 (4)
(4)
The assumption taken within the Equation (4) won't utterly hold in real time therefore any experimental detail is desired. Therefore in IMAR model it performs high separation of speech signal supported the potential assumption is a minimum of part show the sensible validity of this assumption.
The set of Equations (3) and (4) represents the generation of IMAR model for the determined spectral element vector Ou,1. In would like of this mode could also be interpreted as follows. The individual sound signals and therefore the spectral element of the sound supply was given in Equation (4) square measure in a flash mixed at the side of admixture X1-1 to make element Pu,1. Within the Equation (3) the blending of the remaining components gift in element Pu,1 with the multichannel AR system with regression or prediction matrices {Hs,1}= L1 ≤ s ≤ L1+s1-1 to come up with the determined spectra element vector Ou,1.
Figure 3 represents the Instantaneous Mixing plus Auto Regressive (IMAR) model. The latent spectral part vector is unperceivable by element Pu,v. The separation matrices and prediction matrices parameters of IMAR model over the whole frequency vary is denoted by ΦW and ΦG. The subsequent expressions represent the set of separation matrices and prediction matrices as
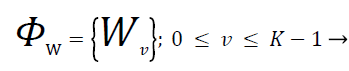 (5)
(5)
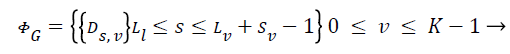 (6)
(6)
By mistreatment the most probability estimation the perfect values of IMAR model parameters ΦW and ΦG. The parameter values of the supply spectral part vectors area unit calculable from Equations (3) and (4). The matrix type is described for the IMAR model within the MIMO filter which supplies the link between the IMAR model and also the frequency domain. The expression for matrix type of Xs,v as
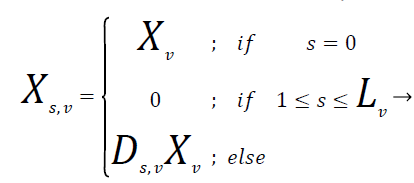 (7)
(7)
Where 0 is a zero matrix. Then (3) and (4) may be summarized in one equation as
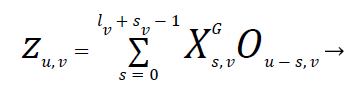 (8)
(8)
Experimental Results and Discussions
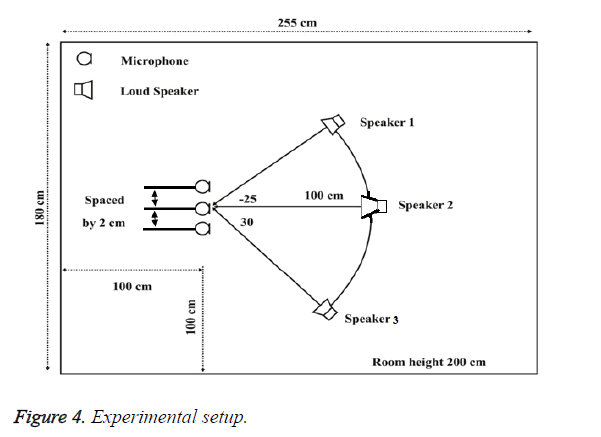
In the projected technique 2 sources and 2 microphones are used for testing the speech signals. The whole take a look at used a group of TIMIT corpus which has thirty eight male speakers, eight feminine speakers and a hundred forty five utterances. The sampled frequency used for the testing of acoustic signals of those utterances is fourteen kc and therefore the information measure is restricted between seventy rate to four kc frequency vary. The data’s from twenty six male speakers are taken and it will be wont to from male-male utterances pairs and therefore the data’s from five feminine speakers are taken and it will be used for feminine-feminine utterances pairs. The remaining data’s from twelve male speakers and three feminine speakers are taken and it will be paired to make the remaining utterances. Thus in total fifty five male-male, twenty feminine-feminine and seventy malefeminine utterances pairs were generated. We have a tendency to take every utterances combine and it will be mixed with the acoustic signals of the 2 utterances with the area impulse responses measured in an exceedingly varechoic chamber to simulate signals which may be discovered from the microphones.
Figure 4 shows an experimental setup developed for the present work. The Signal to Interference Ratio (SIR) and the Direct to Reverberation Ratio (DRR) should be evaluated from each trial taken by the experimental setup. The component of IM th microphone signal is given by OIm Is(n) which is originating from the IS th source. Then the value of OIm Is(n) is given by the following equations as
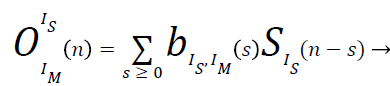 (9)
(9)
The room impulse response is given by {bIs,Im (s)} with s ≥ 0 from the Isth source speech signal to the Im th microphone. The index value of the microphone is obtained from Is where the source speech signal Is appears most prominently as
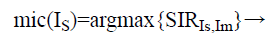 (10)
(10)
By using the source signal Is th the input SIR and DRR value is computed as
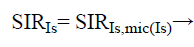 (11)
(11)
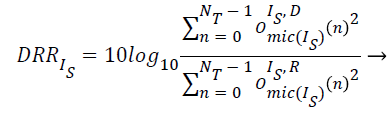 (12)
(12)
The direct reverberation components from the experimental values of OIm IsR (n) are found out from the values of OIm IsD and OIm IsR respectively. So from the above experimental values the direct to dereverberent components are described as
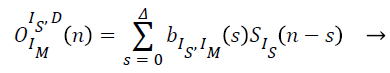 (13)
(13)
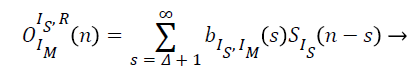 (14)
(14)
From the experimental output every signalling is rotten in keeping with the sources so as to search out the values of signalling to interference quantitative relation.
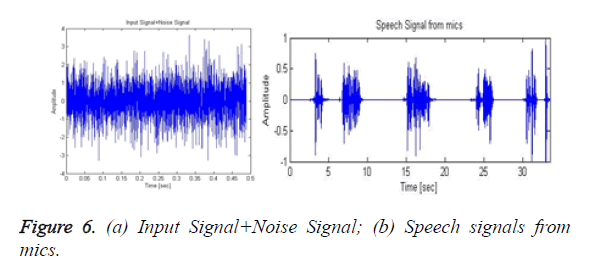
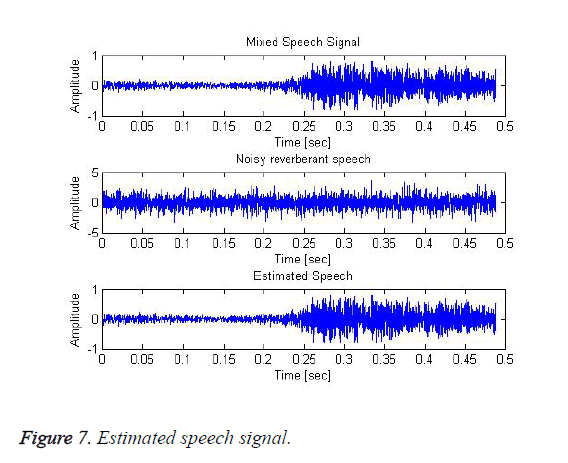
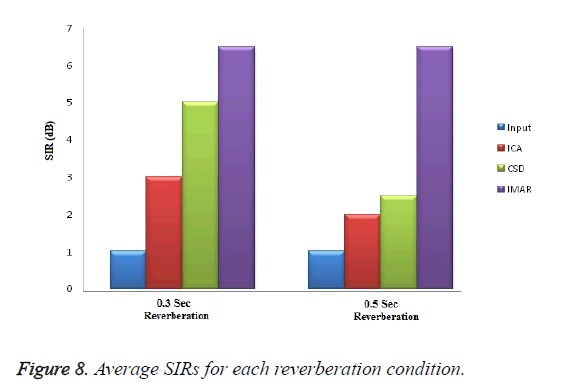
Allow us to think about WIo(n) denote the signalling IO th and WIoIs(n) denote the Is th supply element. For these calculations of process mike signals O1Is(n),….., OImIs(n) with the calculable prediction and separation matrices for conniving the direct to reverberation quantitative relation we'd like the impulse responses from the sources to the outputs. For estimating the impulse responses it uses the smallest amount mean squares matching. The impulse response is calculable from the supply speech signal IS to the output speech signal IO. The matching errors square measure taken by the assumptions of -20 dB. This experimental result indicates the IMAR model is effective for BSS. Figure 5 shows the input samples of speech signals from two sources. The corresponding short time Fourier transform was illustrated in Figure 6. The instantaneous mixing of the samples based on the IMAR model was shown in Figure 7 the separated speech signals of the blind sources are illustrated in different forms for various separable speech signals are given in Figure 8. From that figure we can clearly mentioned the IMAR model gives better outperformed in the frequency domain blind source separation for both reverberation conditions in terms of average SIR.
Figure 8 shows the average SIRs for each reverberation condition. We infer that the methodological difference between the ICA, CSD and IMAR models leads to the difference in SIR improvement. We infer that the methodological difference between the ICA, CSD and IMAR models leads to the difference in SIR improvement. For an experimental study the 0.3 sec and 0.5 sec reverberation time are considered. The effects of male voices and female voices for the separation of speech signals are estimated. Table 1 represent the average changes in SIR and DRR for male female and female male pair by taking speaker 1 is male then speaker 2 is female and another one is reverse of this.
| Gender | Speaker 1 | Male | Female |
|---|---|---|---|
| Speaker 2 | Female | Male | |
| Speaker 3 | Male | Male | |
| SIR | Speaker 1 | 5.21 | 4.72 |
| Speaker 2 | 5.26 | 4.88 | |
| Speaker 3 | 5.3 | 4.92 | |
| DRR | Speaker 1 | 4.32 | 4.12 |
| Speaker 2 | 4.51 | 4.42 | |
| Speaker 3 | 4.68 | 4.58 |
Table 1. Average sir and DRR increases in decibel.
Application of blind source separation in the field of biomedical engineering
Spectrographic displays: A spectrogram is a display of the magnitude of the short-time Fourier transform of a signal as a function of both time and frequency. For sound signals, restriction to the magnitude of the STFT is usually justified because the ear is not very sensitive to the phase of the shorttime spectrum. Spectrograms can be displayed either by encoding energy on a gray scale, or as perspective representations. Gray-scale displays are particularly convenient, and were produced by analog spectrographic instruments in the 1940’s, long before digital spectrograms became available. Analog spectrograms were generated by passing the signal through a bank of analog band pass filters, then computing the short-time energy at the output of each filter by rectifying and low pass filtering the band pass filter outputs. Modern, digital spectrograms are obtained by computing fast Fourier transforms of successive signal segments. Two bandwidths are widely used in spectrographic analyses of speech: Broadband spectrograms, which have a frequency resolution of 300 Hz, and narrowband spectrograms which have a resolution of 50 Hz.
The frequency resolution of the narrowband spectrogram is sufficient to resolve individual harmonics of the fundamental frequency of voice (˜100 Hz). These harmonics appear as horizontal bands during voiced portions of speech. On the other hand, the broadband spectrogram has sucient time resolution to resolve individual opening and closing of the vocal cords, which appear as vertical striations during voiced segments. Thus, the periodic vibration of the vocal cords appears as vertical striations in broadband spectrograms, and as horizontal bands in narrowband spectrograms. The broadband spectrogram also reveals the short noise bursts of stop consonants and rapid changes in formant frequencies.
Conclusion
The present work is disbursed to style the effectively separate of speech signal from the blind source Separation by victimization technique of fast admixture motor vehicle Regressive method and also the most probability perform. The key options given within the fast admixture motor vehicle Regressive methodology is that optimized separation of speech signals and thereby facultative U.S. to perform a blind supply separation method in thought. Within the gift methodology the signal to interference rate improves over half dozen decibel. By victimization fast admixture motor vehicle Regressive methodology it earned sensible signal to interference quantitative relation and direct to reverberation quantitative relation even once a reverberation time was 0.3 s. it's complete that the fast admixture motor vehicle Regressive methodology provides a robust tool for mike array signal process during a reverberative area impulse response. This stage theoretically needs the perfect knowledge of the noise covariance. Now, if compare the performances provided by each method. To conclude, the selection of a BSS method should be driven by hypotheses and considerations issued from application objectives such some statistical/physiological prior information on the sources and the additive noise.
References
- Nakajima H, Nakadai K, Hasegawa Y, Tsujino H. Blind Source Separation with Parameter-Free Adaptive Step Size Method for Robot Audition. IEEE Transact Audio Speech Lang Process 2010; 18: 1476-1485.
- Naqvi SM, Yu M, Chambers JA. A Multimodal Approach to Blind Source Separation of Moving Sources. IEEE J Select Topics Signal Process 2010; 4: 895-910.
- Wang L, Ding H, Yin F. A Region-Growing Permutation Alignment Approach in Frequency-Domain Blind Source Separation of Speech Mixtures. IEEE Transact Audio Speech Lang Process 2011; 19: 549-557.
- Nesta F, Wada TS, Biing-Hwang J. Batch-Online Semi-Blind Source Separation Applied to Multi-Channel Acoustic Echo Cancellation. IEEE Transact Audio Speech Lang Process 2011; 19: 583-599.
- Tsung-Ying S, Chan-Cheng L, Shang-Jeng T, Sheng-Ta H, Kan-Yuan L. Cluster Guide Particle Swarm Optimization (CGPSO) for Underdetermined Blind Source Separation with Advanced Conditions. IEEE Transact Evolution Comput 2011; 15: 798-811.
- Clark FSP, Petraglia MR, Haddad DB. A New Initialization Method for Frequency-Domain Blind Source Separation Algorithms. IEEE Signal Process Lett 2011; 18: 343-346.
- Da-Zheng F, Zhang H, Zheng WX. Bi-Iterative Algorithm for Extracting Independent Components From Array Signals. IEEE Transactions on Signal Processing 2011; 59: 3636-3646.
- Nesta F, Omologo M. Generalized State Coherence Transform for Multidimensional TDOA Estimation of Multiple Sources. IEEE Transact Audio Speech Language Process 2012; 20: 246-261.
- Jen-Tzung C, Hsin-Lung H. Convex Divergence ICA for Blind Source Separation. IEEE Transact Audio Speech Lang Process 2012; 20: 302-315.
- Gunther J. Learning Echo Paths During Continuous Double-Talk Using Semi-Blind Source Separation. IEEE Transact Audio Speech Lang Process 2012; 20: 646-664.
- Marin-Hurtado JI, Parikh DN, Anderson DV. Perceptually Inspired Noise-Reduction Method for Binaural Hearing Aids. IEEE Transact Audio Speech Lang Process 2012; 20: 1372-1382.
- Choi S, Cichocki A, Park H, Lee S. Blind source separation and independent component analysis: A review. Neural Inform Process Lett Rev 2005; 6: 1-57.
- Amari S, Douglas SC, Chichocki A, Yang HH. Multichannel blind deconvolution and equalization using the natural radiant. Proc IEEE Workshop Signal Proc Adv Wireless Commun 1997, 101-104.
- Douglas SC, Gupta M. Scaled natural gradient algorithms for instantaneous and convolutive blind source separation. IEEE Acoust Speech Signal Process 2007; 2: 637-640.
- Liu J, Xin J, Qi Y, Zeng FG. A time domain algorithm for blind separation of convolutive sound mixtures and l1 constrained minimization of cross correlations. Commun Math Sci 2009; 7: 109-128.
- Murata N, Ikeda S, Ziehe A. An approach to blind source separation based on temporal structure of speech signals. Neurocomp 2001; 41: 1-24.
- Parra L, Spence C. Convolutive blind separation of nonstationary sources. IEEE Trans Speech Audio Process 2000; 8: 320-327.
- Smaragdis P. Blind separation of convolved mixtures in the frequency domain. Neurocomp 1998; 22: 21-34.
- Zibulesky M, Pearlmutter BA, Bofill P, Kisilev P. Blind source separation by sparse decomposition in a signal dictionary. TR No. CS99-1, University of New Mexico, Albuquerque, 1999.
- Vielva L, Erdogmus D, Pantaleon C, Santanmaria I, Pereda J, Principe JC. Underdetermined blind source separation in a time-varying environment. Proc ICASSP 2002; 3: 3049-3052.
- Deville Y. Temporal and time frequency correlation-based blind source separation methods. Proc ICA 2003; 1059-1064.
- Rickard S, Yilmaz O. On the approximate w-disjoint orthogonality of speech. Proc ICASSP 2002; 1: 529-532.