Research Article - Biomedical Research (2017) Artificial Intelligent Techniques for Bio Medical Signal Processing: Edition-I
A novel fast chaff point generation method using bio-inspired flower pollination algorithm for fuzzy vault systems with physiological signal for wireless body area sensor networks
MV Karthikeyan1* and J Martin Leo Manickam21Department of Information and Communication (PT), Anna University, Tamil Nadu, India
2Departnment of Electronics and Communication Engineering, St. Joseph’s College Of Engineering, Tamil Nadu, India
- *Corresponding Author:
- MV Karthikeyan
Department of Information and Communication (PT)
Anna University
Tamil Nadu, India
Accepted on February 15, 2017
Abstract
Now-a-days various In-body Medical Sensors (IBMS) are used to treat and monitor patient’s medical condition continuously, so it has become mandatory to attach a wireless module to these IBMS. This allows the doctors to re-program the IBMS with programming devices wirelessly. This makes it easy for the attackers to take control of the highly protected In-Body Medical Sensor. A normal high computational, more complex and more memory consuming cryptographic code cannot be used in devices like wireless sensor nodes. This IBMS is a tiny wireless device with very limited memory. It must be provided with device compatible security code, to be protected from attacks. Thus, fuzzy vault scheme in Biometric cryptosystem is used in protecting user medical data in real world with a wide range of attacks, but the main demerit is the user medical data is highly visible and the randomly generated chaff points are also easily identified by the attackers who want to hack the data for illegal purposes. A fuzzy vault is chosen because of its infeasibility of reconstructing the polynomial at the receiving end. In order to improve the vault performance, more number of chaff (noise) points is added in a shorter duration. This paper uses a Bio-inspired Flower Pollination Algorithm (FPA) for generating more chaff points in a short duration. Studies show that, using the FPA for the chaff point generation with least input information and can start generating the chaff points in just 0.49 msec. We have presented the simulation result for the proposed fast chaff point generation using Bio- inspired Flower Pollination algorithm in fuzzy vault for WBAN and observed faster chaff point generation and a good acceptable level of ROC.
Keywords
Flower pollination algorithm, Chaff point, Fuzzy vault, Lévy flights, Polynomial creation, ECG.
Introduction
Data security is the guarantee that assures confidentiality, integrity and availability of data across hardware and software. Biometrics is one of the latest technologies that use the physiological feature of a person in order to identify him. Most of the developed authentication crypto systems have well known flaws and weaknesses, which are easily identified by the malicious parties and data being exploited. There are many other security schemes are available which are unbreakable even by brute force attacks [1]. This study proposes Biometric signal authentication using the Biometrics obtained from the human itself as they are less expensive, friendly and relatively safer. In a large distributed and insecure environment, key storage and key access are the main concerns of the cryptographic schemes. Currently, using passwords for the protection of data is one of the secure methods, but the passwords can be easily stolen or a dictionary attack can be made on that corresponding data and the key can be recovered. Many other security threats exist in the current cryptography like denial-of-service (DOS), smartcard forgery and parallel attack. Physiological signal (Biological signal) authentication schemes grant access to the user data when the same sample of physiological signal is matching at the input verification at receiver’s end and processing it over the efficient cryptosystem is called Biometric cryptosystem. It is one of the most efficient and conventional methods, and it handles a double layer of security. Therefore, extraction of the secret key is computationally impossible. Another method is Transformation based cryptosystems in which the biometric features are converted to another irreversible form and matched with the other end converted form. Once matched, it is authenticated successful.
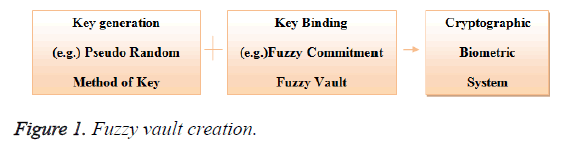
Biometric cryptosystem is divided into three categories: key generating, key binding and key release. The key generating (i.e. the cryptographic key) proposals are large in number [2-5] and the most common method is Pseudo Random Number generation. While key binding is the second category, where the secret key and the physiological data [ECG signal unique peak in this case] are combined Figure 1 shows a simple binding. Various key binding schemes are proposed, one is the fuzzy commitment scheme, which is [6] used to hide the secret key using the physiological set of data [from the pacemaker or In–Body Medical Sensor]. As these physiological signals are unique in nature, it is used for granting authentication of medical sensors. The physiological signals cannot be changed or replaced but when stolen, can be used in many illegal ways. Since the loss of patient related medical data by the hospital is against law, it must be protected. But as such, physiological signals cannot be stored as they are because they do not have any security structure like that of cryptographic schemes. Hence, various stages of security have to be included. In the above mentioned cryptographic schemes all have their own merits and demerits. The physiological signal which is unclear and non-coherent by nature has its merits of fuzzyness. No two physiological signals are perfectly identical and the vault system which is unbreakable with their own merit and can be made to overcome each other’s demerits. Thus, creating an extremely strong and untraceable authentication system in which a cryptographic key is secured by a physiological signal combined with cryptography is called fuzzy vault [7]. On successful decoding of the polynomial, the secret key is revealed. Thus, the most computationally inclusive and complex task in the fuzzy vault scheme is the chaff point generation. That is nothing but noise points which mimic that of the original physiological extracted unique feature points. These chaff (noise) points are used the hide the valid points inside to fuzzy vault.
Related Works
The Body Area Sensor node, ECG signal pattern, Attacks and the fuzzy vault solutions in protecting these human vital signs have been widely discussed in the survey [8]. This work has proposed a solution for the chaff point generation which needs attention. Many other research works use cryptographic key generation from physiological data and protect them by using various techniques like hashing, chaotic mapping and scrambling, another new method proposed by Dodis et al. using fuzzy vault method had completely eliminated the chaff points [9] which is not of concern to this paper. The vault creation is a standard polynomial formation using a secret key and combination of physiological feature point’s projection over it in order to form a fuzzy vault. The physiological based fuzzy vault scheme uses a set of chaff points to lock the physiological signal (ECG signal) based on feature extracted from unique points inside the vault. The secret key is expressed in the form of a polynomial and the unique points of physiological signal are projected over it.
The proposed model is based on the method proposed by Venkatasubramanian et al. [10], where chaff point generation is the most crucial function. There are two rules to be followed in the designing. Firstly, the chaff point generated should not come too close or must not overlap on any genuine valid points in order to prevent false negative. Secondly, the chaff point must not fall on the polynomial coefficients that direct the secure random key. The first proposed idea for chaff point generation by Juels et al. [7] a random point is generated and is pre-distributed inside the sensor and checked for satisfactory action of the fuzzy vault scheme in an efficient manner by consuming less memory space of the sensors in the given network.
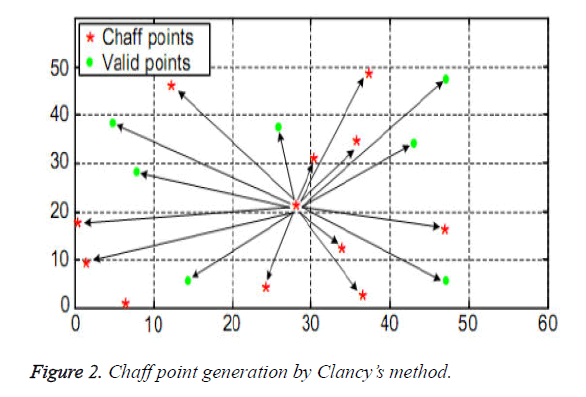
In another method Clancy et al. [11] proposed the chaff point generation, where a minimum distance δ=10.7 is maintained between all the chaff points and from the valid point. The Euclidian distances were calculated on the chaff points generated to satisfy the first conditions met by the chaff point generation rule. He generated a random point in the x-y universe of the valid points and existing chaff point and then, calculated the Euclidian distance between the new random point generated with all other existing points [both of chaff and valid].For the acceptance as a chaff point, it should have a minimum distance of δ with others points in the universe. Otherwise, the point is eliminated and a new chaff point (random) is generated. This process is repeated until the required number of chaff points are generated for the fuzzy vault process. Once the level is reached, the chaff point generation process comes to an end [stops].
The simplified chaff point generation structure is shown in the Figure 2 which contains 940 valid points and 25 chaff points. To generate the first chaff point the Euclidian distance is executed ten times, to generate the second chaff point Euclidian distance is executed eleven times. Thus when the valid point increases the number of times of the Euclidean execution also increases linearly and the Euclidean method of distance calculations also includes squares and square root in its operation. Consider an instance to find a chaff point the Euclidean distance must be calculated to its total sum of valid point and chaff. Also, the total sum of Euclidean distance increases with the increase in chaff points as some chaff points generated will be unsuitable due to its close existence with a valid point or chaff point and will be eliminated after the Euclidean calculations are performed. Thus, this method increases the computational overhead.
In 2004 and 2005, Uludag et al. proposed a notified and extended work on both fuzzy vault and chaff point generation systems. In 2004, he proposed the Chaney’s method with δ=25 [12] distance which maintained a maximum distance with other points. In this method the excess computation was reduced as no point would come in close proximity with them as all were twice the distance away compared to the Clancy’s method of chaff point generation. But this method has an advantage of easy identification of chaff points as they were far from each other. In 2005, Uludag et al. proposed [13] a notified fuzzy vault system that used both valid point location and orientation attributes for fuzzy vault. This made the method more secure and difficult to decode for an attacker. The proposals using Clancy’s methods for chaff point generation had the disadvantage of high complexity and more time consumption, when the number of chaff points generated was high.
In the recent year 2010, the author Khalid et al. proposed [14] a dynamic and efficient system for the generation of chaff points. They have brought down the most critical and intense chaff point generation method to a lightweight and novel chaff generation algorithm using the circle parking method. The distance (δ) between the points was maintained greater than half the distance (>δ/2). When a new chaff point had to be added in the generation, it should be greater than the boundary distance (δ/2) to avoid overlapping with existing points. Then, it was added to the fuzzy vault as a valid chaff point. The fuzzy vault used fingerprint as Biometric data where the miniature location, minutiae orientation and minutiae are used in the construction of the fuzzy vault. The test result shown, gave 140 times faster than existing Claney’s method for generating 500 chaff points and the operations were reduced from O(n3) complexities to O(n2) complexity. In order to reduce the computation complexity, the authors utilized addition, subtraction and comparison instead of squaring and square root operation for the generation of chaff points which may be a renowned action in generation of chaff point but could be a cause for other problem due to its change in arithmetic operation. Also, this method needs more time to check whether a valid point or a chaff point is created on the boundary.
Ngvyen et al. [15] proposed the new fast chaff point generation algorithm. This proposed algorithm randomly generates a chaff point in the image cell and was decided as a new chaff point if it was a unique chaff in that image cell and the distance between the adjacent points was(>δ) greater than δ it was added to the system. This algorithm reduced the computation time, with a computation complexity less than O(n2) (n is the total chaff point).where the clancy’s and Khalil system need 66,609 and 1,17,605 iterations for generating 240 chaff points respectively. The proposed state of the art work needs only 3276 iterations to generate the same value of chaff point .This method achieves 14.84 times and 41.86 faster than existing Clancy’s and Khalil scheme for generating 240 valid chaff points. This improved fast chaff point generation scheme for vault of Biometric values can produce 11% more number of chaff points in comparison with the contemporary fast chaff point generation developed by Khalil method. Due to the longer computation time of Khalil and clancy’s, which is about 20.33 times and 35.89 times this scheme, it is considered as the pinnacle in the generation of chaff point.
Fuzzy Vault Encoding and Decoding
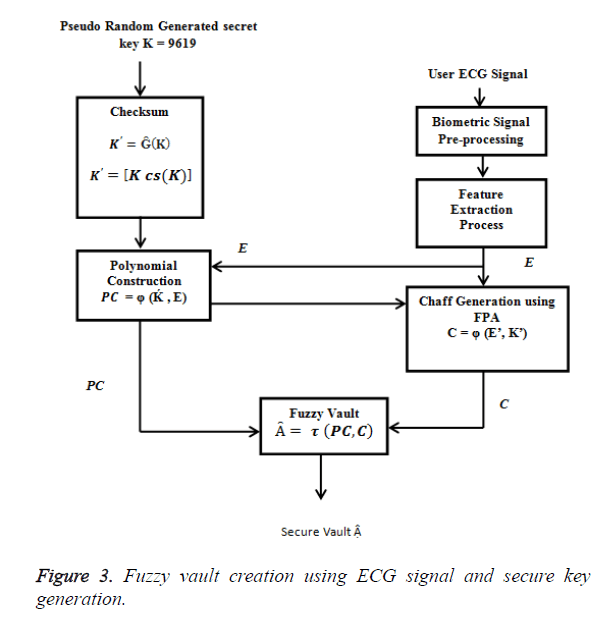
Figure 3 shows the Biometric [Encryption] cryptography (BC) system that shows the structure of fuzzy vault scheme, which uses ECG signal peak to bind with the secret key. ECG signal is a unique Bio-signal and cannot be replicated and reproduced. The distinct QRS-complex is taken and the P and T are eliminated as it was found that eliminating these points does not affect the bio-signal uniqueness hence it is eliminated.
Fuzzy vault encoding phase
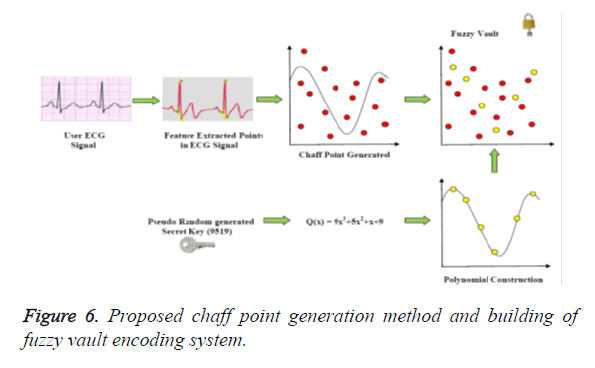
Figure 1 shows the fuzzy vault encoding process. The secret key K is generated by random generation process. The fuzzy vault is applied to hide the random secret key using Bio-signal extracted data. During the encoding process of the system, the randomly generated secret key is structured into a polynomial and the Bio-signal feature extracted values are inculcated into the Figure 3 Fuzzy vault Creation using ECG signal and Secure Key Generation polynomial and the resultant values (lock set) is the secure fuzzy vault.
In the fuzzy vault locking process the secret key K is a row matrix of random number of longer string length as shown in Eq. (1) .The K is concatenated with its check sum to form a new dimensional cryptographic key K’ as shown in Eq. (2). Each ki Є K is the ith coefficient to form a polynomial Q(x) where the degree of the polynomial is (g-1) as shown in Eq. (3).
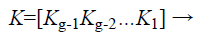 (1)
(1)
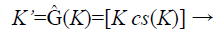 (2)
(2)
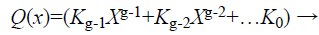 (3)
(3)
Ĝ is the parameter that performs the checksum operation for K and concatenates with the K. To get the Ḱ value, the Bio-signal feature extraction system consisting of ECG signal processing algorithms that extract P, Q, R ,S and T which are the Peak values from the user’s Bio-signal are taken as ECG coordinates and represented by a column matrix, E as shown in Eq. (4) .
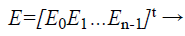 (4)
(4)
Xmj is the X-axis coordinate and Ymj is the Y axis coordinate. While n is the maximum number of peak points found in the ECG signal input from the user. Each ECG signal peak coordinate is then concatenated to form the X axis values for the fuzzy vault. This data set is plotted onto the polynomial equation Q(x) in Eq.(3) to obtain the Y axis coordinate values. This input builds the polynomial creation equation as shown in Eq. (5).
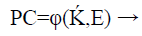 (5)
(5)
φ is the polynomial creation function that fixes the Bio-signal data on the polynomial, which is a simple row matrix that is equal in length of ECG column matrix as shown in Eq. (6).
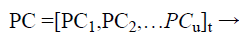 (6)
(6)
The next process in the system is the chaff (noise) point creation block, which generates the chaff point as shown in Eq. (7) by obtaining the valid input points combined from the ECG – signal feature extracted unique points and from the secret key Ḱ which is concatenated with its own checksum.
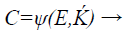 (7)
(7)
Where ψ is the chaff point generation function that generates the noise points in the matrix C. Each noise point (Cxi, Cyi) is utilized for plotting the chaff point. The process is continued until a sufficient number of chaff points have been generated. Generally chaff points have to be at a minimum ratio of 10:1 to the ECG – signal unique points in the fuzzy vault. (Chaff point generation method is explained in the next section using Flower Pollination Algorithm)
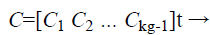 (8)
(8)
Where Ci is the set of values of chaff points, they are multiplied by a constant 10 (κ) for chaff point magnification. The combination of valid and chaff points in an x-y universe forms the fuzzy vault as shown in Equations 9 and 10.
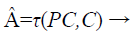 (9)
(9)
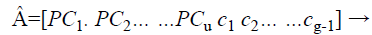 (10)
(10)
Fuzzy vault decoding phase
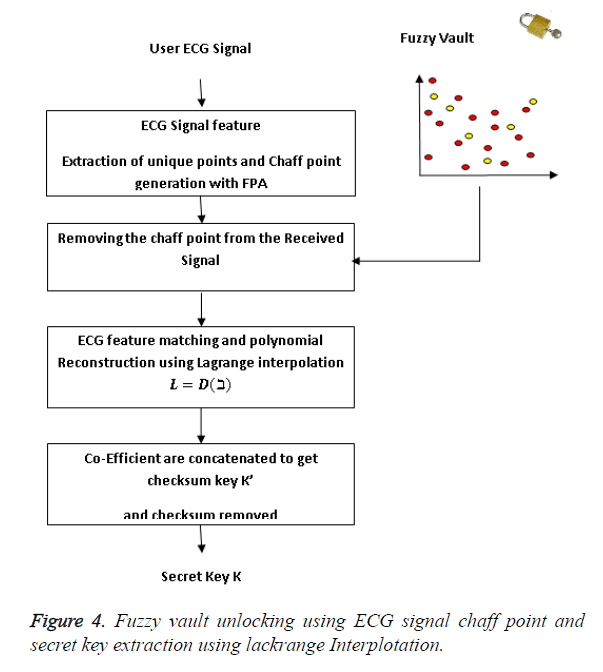
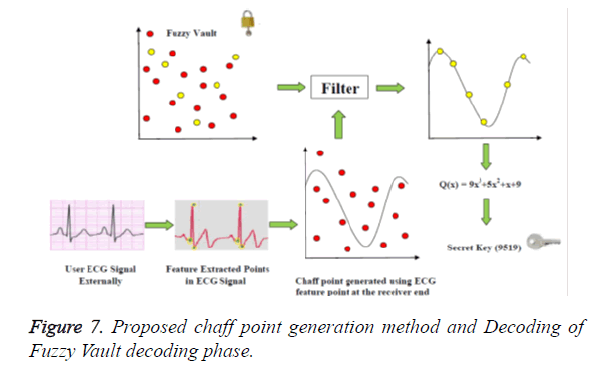
During the decoding phase, the vault is unlocked with the authenticated bio-signal to retrieve the cryptographic key. The Figure 4 shows the fuzzy vault decoding phase where the phase starts by obtaining the Biometric signal from the user to decode the fuzzy vault at the receiving end together with the vault from the encoding part of the system. The Biometric feature containing the user Biometric ECG signal is generated at the receiving end as shown in Eq. (11)
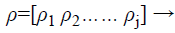 (11)
(11)
Where ρj-1 are the coordinates of ECG – signal feature extracted unique points.
The next operation is the ECG feature matching function as shown in Eq. (12).
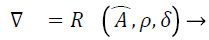 (12)
(12)
The ECG – unique feature set, ρ is the matched point generated at receiver end and the chaff point is matched with the fuzzy vault  are filtered from the received fuzzy vault data.
The remaining sets of coordinates are sent to the polynomial reconstruction block to find the polynomial coefficients. There must be at least f set of coordinates to successfully reconstruct the polynomial or else the decoding process fails. Since it is possible that some of the sets recorded might have been created from noise point rather than genuine Biometric data, the Polynomial reconstruction block tries to reconstruct the polynomial Q(x) based on the points in using the Lagrangian interpolation [10] Eqs. 13 and 14.
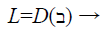 (13)
(13)
Where L=[ωf ωf-1….ω1] → (14)
In the Lagrangian interpolation to find the coefficients of a polynomial of degree f (where the degree n is known to all sensors) it needs n + 1 unique projections to solve the right polynomial. The polynomial Q(x) is constructed as shown in Eq. (15).
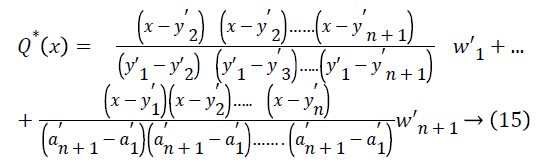
The solution to the Eq. 15 is
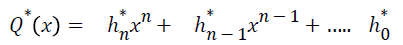 where the coefficient
where the coefficient 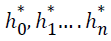 are being extracted and concatenated to form the secret key K . The device stores the K for further data authentication purpose.
are being extracted and concatenated to form the secret key K . The device stores the K for further data authentication purpose.
Flower Pollination Algorithm for Chaff Point Generation
Optimization can be expressed as the technique of finding out the best solution for a given problem. The finding or choosing the best solution can be performed interactively with special mathematical models. In order to find the optimized best solution, various optimized algorithms, referred to as techniques or tools are utilized in solving optimization process of solution generation. The search for optimal solution not only concentrates on the best solution for the given problem, but also the robustness of the solution to be valued in the engineering field. All these millions of years, nature has given a solution for many challenging problems. In the decade between 1950’s to 1960’s many scientists have developed the concept of genetic algorithm [GA] based on Darwin evolution of human system for the optimization of memory space requirement [16].
This leads to the inspiration of evolution in bio-inspired algorithm to circumvent the constraints given by the gradient descent algorithms to search for the optimization problems. With this regard, the Scientists have found out several bio-inspired global optimized algorithms like Particle Swan Optimization (PSO) [17] based on Swan behaviours of fish and birds, Bat algorithm [18], based on Microbat behavior in echo location, fire fly algorithm [19] based on tropical firefly flashing light pattern. Recently, chicken swarm optimization (CSO) [20], Flower Pollination algorithm (FPA) [21], Approximate Muscle Guided Beam Search (AMGBS) [22], Magnetotactic Bacteria Optimization based on Moment Migration (MBOMM) [23] were developed. Of all these, FPA has given a more optimized and robust solution in many applications, when compared to the similar algorithms in the same period, FPA has given solutions for complex and non linear problems even in a faster processing time (Less time for searching optimal solution). A detailed view of the FPA for the application in the proposed algorithm is given.
Now, researchers have used the pollination of flower using its four rules. The aim of flower pollination is to find the fittest and optimal reproduction of plants in many numbers. The main purpose of a flower in a plant is ultimately the reproduction through pollination. Where insects, bats and birds do this unimaginable process of pollination over a longer distance and have done it all these years. This pollination is done for their own development and parallely evolve the same type of plant species over millions of years. The pollination can be broadly classified as biotic and abiotic. When wind and diffusion help in carrying of the pollens it is referred to as biotic which constitutes only about 10% of the pollination, whereas abiotic pollination is the transfer of pollen by honey bees or insects over a longer distance. In this the pollinators follow a pollen vector which is very much diverse. This constitutes 90% of pollination. In these, the honey bees are good examples of pollinators as they tend to visit exclusively certain species of flower while neglecting others which researchers call flower constancy, because the insect can get assured nectar supply which they have found before and stored in the memory with minimal cost of learning and exploring to get guaranteed nectar intake [24]. Another classification of pollination is selfpollination and cross pollination. Self-pollination is a process in which the pollens are transferred from a flower to another in the same plant, where as cross pollination is the one in which the pollen is transferred between two flowers belonging to different plants. e.g. peach.
Local pollination: It is a combination of abiotic and self pollination which occur by wind and when there is no reliable availability of pollens in neighborhood.
Global pollination: It is the best type of pollination and is always preferred because it covers larger area, and the flower constancy is maintained. The particular flower pollination have been increased over a distance and also given the fittest yield, where biotic and cross pollination is combined called Global pollination. The pollinators like Honey bee, birds, Bat and fire fly travel a larger distance (Random path) obeying the Lévy flight algorithm [25] contributing to the global pollination.
Flower pollination algorithm (FPA)
Yang [21] proposed the flower pollination algorithm which is given by the following four rules:
1. Rule 1: Flower pollination is the process formed by the Biotic and cross pollination and the pollens are carried by pollinators that obey Levy flight.
2. Rule 2: Local pollination is the combination of abiotic and self-pollination
3. Rule 3: When there is a proposional (resemblance) between two flowers, the pollinator develops flower constancy that is equivalent to the reproduction of flowers.
4. Rule 4: The Switching probability controls both local pollination and global pollination. S Є [0, 1]. The local pollination can have a fraction S because of physical proximity and other factors such as wind.
To execute a process all the rules are written as formulas. In global pollination the pollen gametes stick to the insects body referred to as pollinators and travel over a consistently longer distance in search of flower pollen constancy, where global pollination is mathematically represented as:
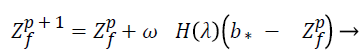 (16)
(16)
Where Zf is the solution vector and Zp f is the pollen at iteration p. b* the current best solution among the available solution during the current iteration. is the scaling factor in controlling the step size of the jump (fly distance of bees).
H(λ) specifies the Lévy flight step size and represents the strength of the pollination. As it can fly over a long distance with random and various step sizes. Lévy flight can be used to explain this random flying characteristic (formed based on the random flight nature of insects) the Lévy distribution can be mathematically written as H>0.
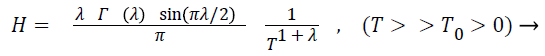 (17)
(17)
Γ(λ) is standard gamma function and this Lévy distribution is accepted for large step size of T>0. In practice T0 can be as small as 0.1, theoretically |T0|>>0.
The step size are generated by pseudo-random number values, that are distanced by the Lévy distribution. Mantegna algorithm [26] is used for jumping the step size with the help of two Gaussian distribution as given in Eq. (18).
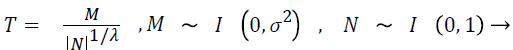 (18)
(18)
Where M~I (0, σ2) which symbolizes that the samples are absorbed from a Gaussian normal distribution with a zero mean and a variance of σ2.
The variance can be expressed as σ2
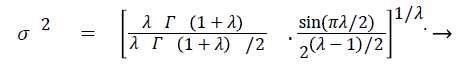 (19)
(19)
When λ=1 is maintained as a constant, the variance equals to unity
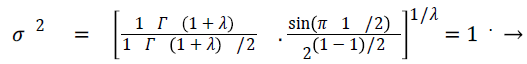 (20)
(20)
Thus the Mantegna algorithm can produce pseudo random numbers. Using these numbers as step size, 50 steps of Lévy flights are generated as shown in Figure 5.
The local pollination, can be expressed as
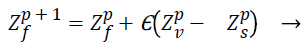 (21)
(21)
The pollen from the same plant species and from different flowers are considered as Zp v and Zp s, this creates a situation that flower consistency is only from the fixed range of neighborhood. When Zp v and Zp s come from the same plant selected from the pollination mathematically it becomes a local random walk if Δ is drawn from an uniform distribution in [0,1]. The flower pollination occurs in various scales both in local and global pollination. The (Rule 4) realizes the situation of the switching probability S, which can effectively switch between intensive local pollination to common global pollination. To have a native role the proximity probability is chosen as S=0.5, but for better result S is taken as 0.8 in various applications for better performance.
FPA algorithm
Initially set the values of the pollen gametes n (population size with random solutions. Initialize the maximum number of Generations as the stopping probability (MNG). The objective is to maximize or minimize the function f (z), z = (z1,z2…,zd). Determine the best solution b* in the population. Identify S Є [0, 1] which decides the switch probability or proximity probability between global and local pollinations. Initializing parameters j and
For (f = 1, f = n; f ++) do
Randomly generated initial population of zi
For all solutions in the population evaluate the fitness function
f (zi)
End for {initialization}
Initialize p=0
While p<MNG
For (f=1; f = n; f++) do (all n flower in the pollination)
Generate a random number rand {rand is a uniform distribution}
If (rand<S) then
Generate a step vector L, (d–dimension)
This obeys Lévy distribution
Proceed Global pollination
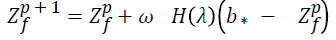
else
Random choose j and k among all the solutions
Draw a parameter ε, where ε [0, 1]
Do local pollination 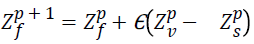
End if
End for
For (f=1; f = n; f++)
Evaluate new solution
Process the fitness function of f (zf) for all solution in the
population
End for
If 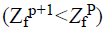 then
then
Set 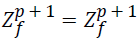 (discard)
(discard)
else
Set 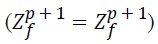 (update)
(update)
End if
Categorize the solution and keep the best solution b* identified from the population Increment ++p
Output the best solution found.
The important parameters settling are n=168; switch probability S=0.8, =0.01 and Lévy flight λ=1.5 (1 ≤ λ ≤ 2)
The Proposed Model for Fast Chaff Point Generation Using ECG Signal Feature Extracted Unique Points
The chaff point generation technique using FPA is discussed in detail in this section. Figure 6 shows the Fuzzy Vault encoding phase. The first phase is the secret key generation by Pseudo random number generation which is used as the coefficient for the polynomial equation. In the second phase, the polynomial coefficient is generated and in this stage, the ECG-signal is sampled from the user from the IBMS for a pre-determined time. With this physiological signal the feature points (QRS-Peak) are generated. The points are plotted over the polynomial equation and the same is used to generate the chaff point. During this chaff point generation both the polynomial input and ECG-features are used, thus no over lapping between the valid points and chaff points occur. (FPA uses Exponential method to generate random points there is no overlapping). In the last phase the chaff points are bound with the polynomial, called the formation of fuzzy vault.
In the receiver end the chaff point is generated using the FPA with ECG signal feature extracted points from outside the body, this chaff points are used to cancel out chaff points present in the received signal (Figure 7). Now the reminiscent is the ECG feature points and the secret key. Once the ECG valid points are removed by using the Lagrangian interpolation method, the secret key is the remaining parameter at the receiving end. This secret key is used in the next authentication process of data transmission, reception and verification.
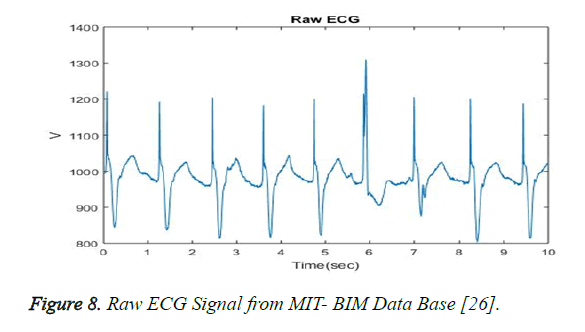
The ECG signals are downloaded from the MIT PhysioBank database, [27] which defines four different types of signals such as European ST-T (EDB) [28], MIT-BIT Normal Sinus Rhythm (NSRDB) [27], MIT-BIT Atrial Fibrilliation (AFDB) [27], MIT-BIT Arrhythmia (MITDB) [27]. The NSRDB and AFDB ECG signals is chosen, as these signals can potentially replicate the pattern from pacemaker or In-Body Medical Sensor. Figure 8 shows a raw ECG signal.
The ECG signal from the user is obtained for a minute, and (4 seconds one PQRST so nearly 60/4=15 Beats~14Beats) approximately 14 beats are obtained. The following are the various stages in extracting the Q,R and S peak from ECG signal stage (ref as feature extracted unique peak points) and later the fast chaff point generation process with FPA.
• Pre- processing.
• Haar wavelet transform.
• Generation of chaff point using FPA.
Pre-processing
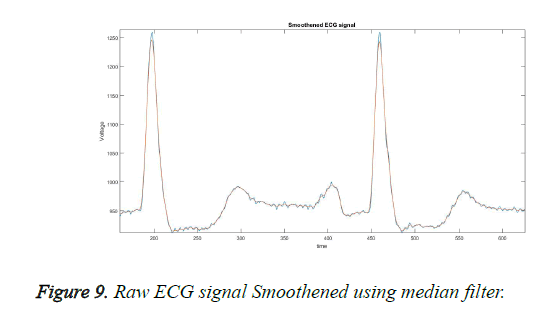
In this block, the ECG signal obtained from the user is given as input and smoothing is done using the median filter [29]. The purpose of using a median filter is to obtain sharp edges and also to reduce the noise present in the ECG signal while recording from the user. It generally fixes its center axis at the middle of the ECG signal and processes. it leaves only the ECG signal removing all other noise and unwanted spikes without changing the original ECG. The smoothened ECG signal is shown in Figure 9.
Haar wavelet transform
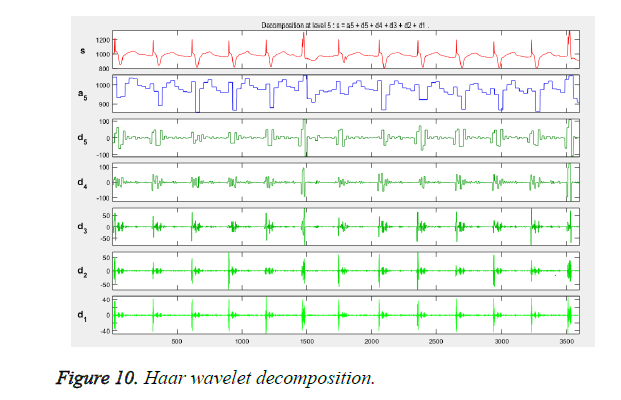
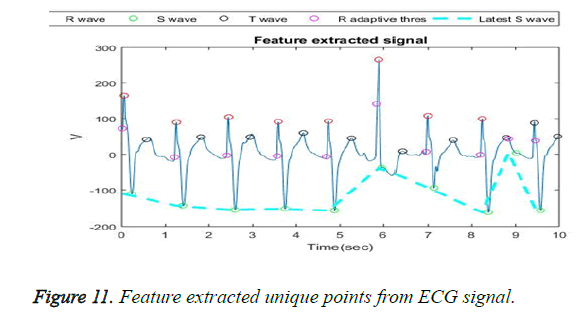
The wavelet transform provides a 21 to 25 level of decomposition [30]. The five levels of decompositions are used on the ECG signal, to elimination noise and power line interference. At the same time, the unique ECG points like P, Q, R, S and T are extracted and the peaks are noted. Figure 10 shows the decomposition. In order to make it narrower, only the QRS peak points are segmented and extracted from the user ECG signal as shown in Figure 11. Thus the feature extracted points are projected in order to generate the chaff point.
Generation of chaff point using FPA
To recognize a person, all the features taken from the ECG signal are required to be grouped. The extracted feature, QRS peak amplitude and their exponential are calculated individually (14 peak each having 3 peaks gives 32 valid point). The individual numbers of feature points in the ECG signal are represented as Qn, Rn and Sn. The entire feature points from the ECG signal are combined to generate the chaff point used in the proposed work is represented as
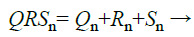 (22)
(22)
The secret key and physiological feature signal are not just enough to create the fuzzy vault, additionally chaff points C are also needed to create the fuzzy vault. Chaff points are the extra added random (noise) points with the feature points that improve the security of the fuzzy vault to its maximum [31]. It is the Flower Pollination based optimization algorithm [21,32] applied to generate the chaff point.
• Initially all the featured points of the ECG signal are taken to generate the chaff points.
• All the extracted feature points of ECG are converted into their corresponding location, which is considered for chaff point generation.
The most important reason we utilized FPA for the optimization is:
• FPA is more optimal\Self Generated (Random points).
• Quick Random Point Generation.
• No overlap of noise points or ECG feature point coefficient.
The FPA is initialized with a population size n (pollen gametes). The following parameter are assigned constant values such as switch probability S=0.8, ω=0.01 and Lévy flight λ=1.5. The ECG signal feature is considered, and unique points are extracted (32 points). First the Q peaks, R peak and S peak are separated. Then around that Q peak in the entire four quadrants, random population size n is generated and the fitness for all the randomly generated population is evaluated (Distance between the random points are found and defined as the fitness). The initial best point (initial best b*) location is identified. Then a random number (rand) is arbitrarily generated from the uniform distribution. In the second stage, the decision is made whether random number comes under Global Pollination (S=0.8) or local Pollination. If the random number value is lesser than the switch probability, the process performed is the global pollination (matched with FPA).next proceed with an exploration process. That is, Jump from the current best vector position to the next random position based on the Lévy flight of distance λ=1.5 .Now calculate the fitness (distance from the current best b*) using the formula
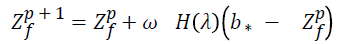
When the random value generated is greater than the switch probability, the condition fails. And the exploration process is performed. During this process the system randomly choose and solutions. The difference in distance between the two randomly generated populations (Zp v-Zp s) and multiplied with a uniformly distributed value Є if (Zp v) and (Zp s) is selected from the same population then it will be local random walk. This value is updated with the current best b* and generates the new current best value Zf p+1. This entire process is defined as local pollination.
Various solutions are updated both in global pollination and in local pollination. The last found value is the optimized distance in which the fitness values of all the newly found random points are evaluated. In this stage we calculate the best chaff point (far from the valid Q point) by updating chaff point list. Best chaff point (global Best) Solution
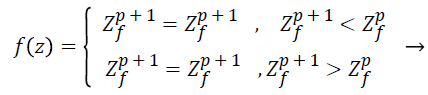 (23)
(23)
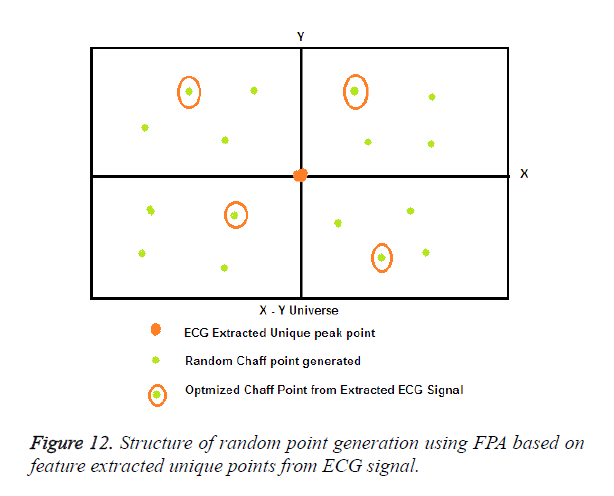
Here the fitness value is calculated as follows: Fitness=max (distance from valid point). When the current best Zp f distance is greater than the new best zf p+1 location, the new best location is discarded and the current best is kept as the global best solution. If the current best xit distance value is lesser than that of the new best zf p+1 then, the new best is updated as the current best location and updated in the list as the global best location. This process is repeated until the max number of iterations (p) is reached. Then, the obtained best location points are converted to the best chaff points generated far away from the ECG signal feature extracted unique points. The number of chaff points generated is represented by C which is grouped to the fuzzy vault in order to maximize the security. This process is concurrently performed for the entire feature extracted ECG R peaks (14 points) and Q peaks (14 points). The random points are generated using the FPA method four in each segment a total of 16, the best one fittest chaff point in four segments are chosen by optimizing the locations and is also shown in Figure 12.
Scheme Evaluation
In this section, the proposed model is made under various experimental analyses. The MATLAB coding is written in order to create the real time working scenario. As taking real time ECG signal from the user pacemakers (IBMS) can be tedious, the ECG signals are downloaded from “MIT –BIT Arrhythmia” database for 20 person’s. A signal for one minute duration from a two- channel ambulatory ECG recording are taken, and sampled at 120 Hz. We had followed the same type of lab procedure and result analysis performed in the papers [32-35].The security analysis and performance of the proposed fast chaff point generation using FPA Scheme is also analyzed using the following metrics
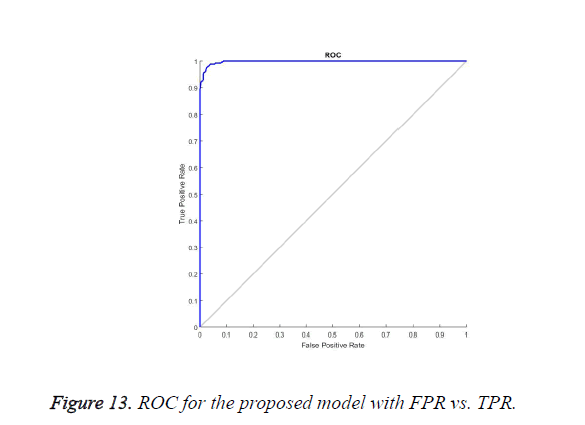
Receiver operating characteristic curve (ROC)
Performance of Fast chaff point generation scheme using FPA is evaluated by using the ROC. The ROC takes the genuine acceptance rate along the Y axis and the False Rejection rate along the X axis. The genuine acceptance rate or True Positive rate is the occurrence of success when an authorized user is allowed to access the data or to decrypt the secret key, when the user has proper chaff point and ECG signal. A false acceptance rate is the other side count of occurrence of the unauthorized user getting successful verification of the data and accessing the secret key without the knowledge of user ECG signal and chaff points. The ROC curve in Figure 13 shows that the success rate or true positive rate increases while the attempt made by unauthorized persons has never occurred. The flat curve of ROC shows that the additional increase in chaff point had improved the integrity, confidentiality and authenticity at the receiver end.
Without the physical contact of the user, the ECG signal can’t be generated from where chaff points are also generated where making a physical contact and receiving the ECG without patient’s knowledge is not possible, it is fast and safe way of generating chaff points by using ECG signal by FPA is one of the best security systems.
ECG signal randomness
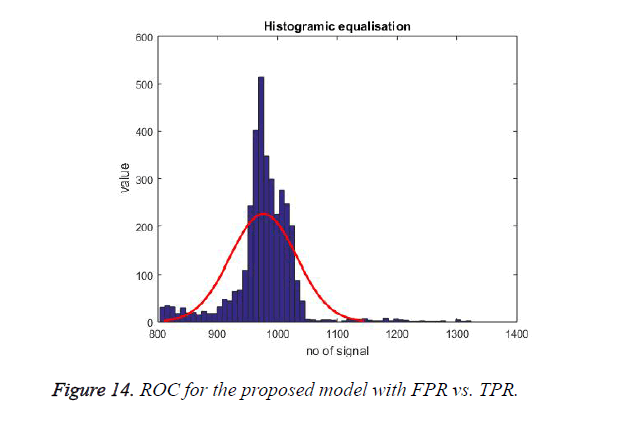
Randomness is a vital requirement in the chaff point, as it is for security purpose. The proposed randomness test defines that chaff points generated are purely random proving all the ECG signal are random in nature. In case of similarity in chaff points, the attacker could retrieve the data. The Histogram of ECG signal for 20 users (at least 1 minute) is shown in Figure 14 it shows that majority of the values fits inside the normal distribution, which indicates the randomness of ECG signal.
Detection of error (DOE)
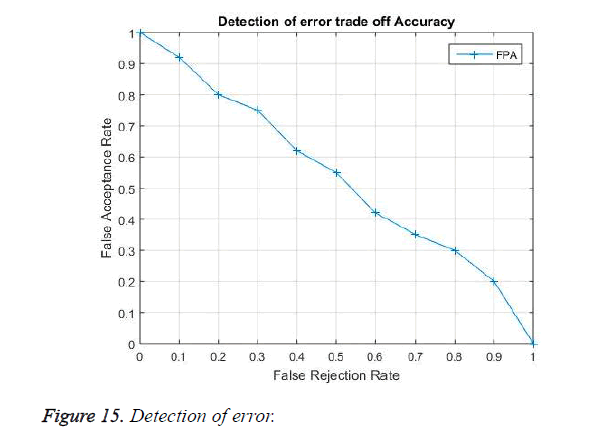
It shows the error rate parameter in the proposed model. The graph is plotted with False Acceptance Rate (FAR) and False Rejection Rate (FRR). The analysis is performed to estimate weather the system could tolerate more distinct valid and chaff points between the sender and receiver end. The curve shows the two critical parameter which must be considered while evaluating the Bio-medical signal security. The FAR is the measure of success in decrypting the secret key from the received signal by using the user’s historical ECG data or data from other patient, while FRR is the measure of in failure in decrypting the secret key at the receiver end with the simultaneous ECG signal obtained from other part of the body. In Figure 15 experimental result shows FAR with FRR on ECG data base. We observe that when FAR is unity the FRR in null in value, when FRR it is kept on increasing the FAR meets a Zero, this implies a balance in the error rate performance of the proposed method.
False acceptance rate
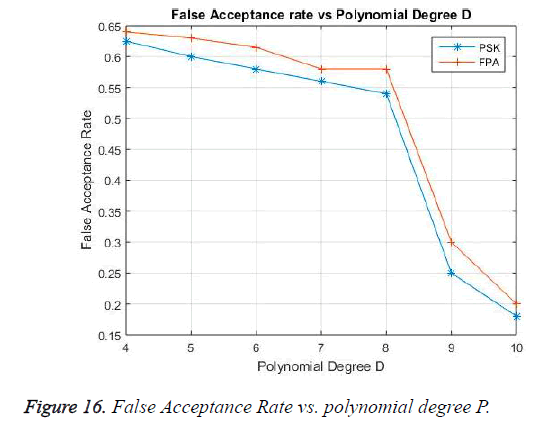
The False Acceptance Rate performance is shown in Figure 16, the False acceptance is the decryption of the received secret key with an incorrect Biomedical signal. FAR is a critical case, which must be considered in Bio-medical security .which keeps the unwanted user from accessing the data. The degree of polynomial ‘P’ is varied from 5 to 10. When the polynomial degree is less, the acceptance of mismatched feature points is maximum affecting the security. With the polynomial degree increase (P=10). The success rate of False Acceptance is reduced to a minimum value. The performance of the proposed algorithm is compared with existing PSK [10] showing a satisfactory result in data security.
False rejection rate
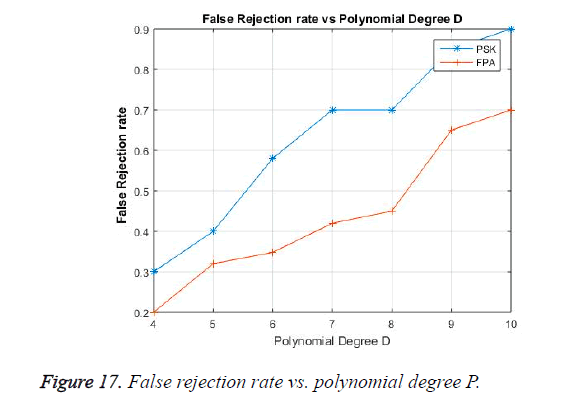
The False Rejection Rate is the inability of the user in decrypting the received signal with the correct ECG signal observed from the authorized user in simultaneous time from other part of the body. It is shown in Figure 17 with a polynomial degree ‘P’, the FRR gradually increasing. This is due to the fact that when the polynomial value is less the similarity between the feature points is more .when the polynomial increases the similarity between the feature points of the two signals from the same user differentiates and increases the FRR. Thus while designing a fuzzy vault the degree of the polynomial must be properly chosen for optimum false acceptance and false rejection rate.
Quick start in generation of chaff point
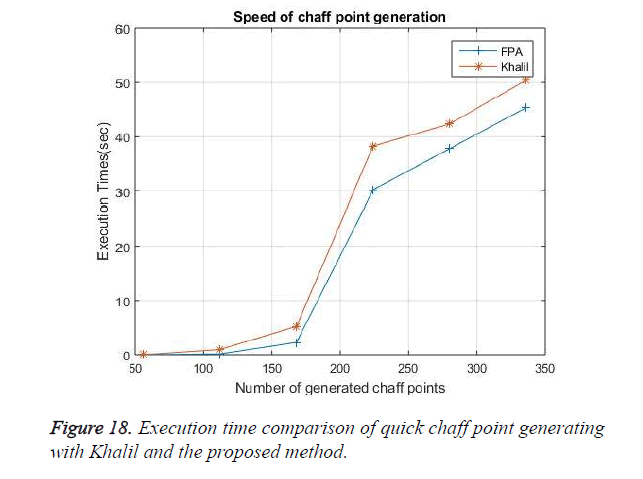
The aim of the proposed model is to generate the chaff point as fast as it can, so that more time and energy is not wasted in the security model. Thus an optimized Flower pollination Algorithm is used in generating these chaff point. This FPA generates the random points around the ECG feature extracted valid points and by using the fitness test and the best points are identified which is then fixed as chaff points. This process is so quick that 168 chaff points are generated within 0.164 seconds. A comparative analysis is shown in Figure 18 with the khalil [14] existing fast chaff point generation algorithm.
This quick start in chaff point generation is achieved by the flower pollination algorithm, as the random points are generated very fast. The optimized value search is also done by Honey bee method. The FPA does not have much complex operation in the chaff point generation which forms the reason for less time consumption. The following table shows the various input ECG peak points, their extracted peak points, total number of random points generated in all quadrants and the selected optimal chaff point with their time.
| S. No | Number of ECG signal | Unique Peak feature detected and extracted from the ECG signal | Total Number of Chaff Point Generated | (optimized) valid number of chaff points generated | Execution Time in (sec) |
|---|---|---|---|---|---|
| 1 | 10 | 30 | 480 | 120 | 0.122 |
| 2 | 12 | 36 | 576 | 144 | 0.143 |
| 3 | 14 | 42 | 672 | 168 | 0.164 |
Table 1. The number of ECG signals detected, unique peaks Extracted from it, Chaff point generated, optimized chaff point generated and the execution time (16 random points generated for a single peak, four per segment).
| S. No | Number of ECG signal | Unique Peak feature detected and extracted from the ECG signal | Total number of random points generated | (optimized ) valid number of chaff points generated | Execution time in x (sec) |
|---|---|---|---|---|---|
| 1 | 10 | 30 | 960 | 240 | 0.162 |
| 2 | 12 | 36 | 1152 | 288 | 0.187 |
| 3 | 14 | 42 | 1344 | 336 | 0.212 |
Table 2. Number of ECG signals detected, unique peaks Extracted from it, Chaff point generated, optimized chaff point generated and the execution time (32 random points generated for a single peak, eight per segment).
| S. No | Number of ECG signal | Unique Peak feature detected and extracted from the ECG signal | Total number of random points generated | (optimized ) valid number of chaff points generated | Execution time in (sec) |
|---|---|---|---|---|---|
| 1 | 10 | 30 | 1440 | 360 | 0.226 |
| 2 | 12 | 36 | 1728 | 432 | 0.241 |
| 3 | 14 | 42 | 2016 | 504 | 0.265 |
Table 3. Number of ECG signals detected, unique peaks Extracted from it, Chaff point generated, optimized chaff point generated and the execution time (48 random points generated for a single peak, twelve per segment).
Conclusion
In this paper an efficient fast chaff point generation method by using the bio inspired Flower Pollination Algorithm with ECG signal feature extracted unique points as the valid points in generating it. The optimization algorithm FA helps us in choosing the best chaff point location for creating a high level of security when combined with vault. The FPA method enables random point generation around valid points and the selection of the best chaff point in the shortest time duration. It is observed that for creating a minimum of 480 random points and selecting of 120 chaff points, the system takes the least time span of 0.122 seconds which is comparatively fast. In addition, the proposed algorithm also maintains the adequate level of ROC when considering other systems. Thus, a fast and distinct non-overlapping and highly random and unpredictable chaff points are generated using the FPA which effectively protects the secret key. Still we need to further investigate the various bio-inspired algorithms in fuzzy vault for chaff point generation to make it simple and faster in protecting WBAN device security. In future the proposed algorithm is implement in FPGA processor and can be analyzed.
References
- Schneier B. Applied Cryptography, 2nd Ed. John Wiley & Sons, USA, 1996.
- Chang YJ, Zhang W, Chen T. Biometrics-based cryptographic key generation. IEEE Int Conf Multimedia Expo (ICME) 2004; 3: 2203-2206.
- Vielhauer C, Steinmetz R, Mayerhofer A. Biometric hash based on statistical features of online signatures. Sixtieth Int Conf Pattern Recognition 2002; 1: 123-126.
- Dodis Y, Reyzin L, Smith A. Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. Proc Int Conf Theory Appl Cryptographic Tech 2004; 3027: 523-540.
- Kanade S, Petrovska-Delacretaz D, Dorizzi B. Generating and sharing biometrics based session keys for secure cryptographic applications. Fourth IEEE Int Conf Biometrics: Theory Applications and Systems (BTAS) 2010.