Mini Review - Materials Science and Nanotechnology (2018) Volume 2, Issue 1

A noble approach to compute the magnetic flux density, magnetic force distribution and its application on magnetic levitation.

Department of Electrical Engineering, Institute of Engineering (IOE), Pulchowk Campus, Nepal

*Corresponding Author:

Amrit Panthi
Department of Electrical Engineering
Institute of Engineering (IOE)
Pulchowk Campus
Nepal
Tel: +977 9840066285
E-mail: 071bel304@pcampus.edu.np

Accepted date: May 09, 2018

Citation: Panthi A. A noble approach to compute the magnetic flux density, magnetic force distribution and its application on magnetic levitation. Mater Sci Nanotechnol. 2018;2(1):32-39.

Abstract

In this work a novel method is introduced for the computation of magnetic flux density and magnetic force of attraction. In the first step, equations for the magnetic flux density are derived using scalar and vector potential along with Helmholtz decomposition equation. Concept of origin shifting and geometrical shape compensation is used to formulate the formula. This concept is further used for the analysis of magnetic field distribution in space around for permanent magnet. Secondly, Equation of force in one dimension is used to model the system both electrically and mathematically to obtain the overall transfer function. In order to reduce the settling time, PID control system is used. Finally, an excellent and robust nature of levitating system is demonstrated by means of simulation studies in MATLAB and measurement results.

Keywords

Magnetic field, Hypergeometric series, Magnetic strength, MRI scanner.

Introduction

In ancient times, magnetism was believed to be the magical force. With the transition of time, many researches and scientific breakthrough has taken place. At this date, we are very much familiar with that magical force. The spin and the orbital motion in an atom cause the magnetism but there are plenty to be explored and discovered about the cause and property of magnetism. The source of magnetism is partly the rotation of magnet and partly revolution around the nucleus. The unfilled electron in the atom gives rise to magnetism [1]. A filled atomic shell has equal number of electrons consisting up and down spin which results in zero magnetic fields. On the other hand, an unfilled shell, results in small magnetization from the orbiting electrons which in turn results in a non-zero net magnetic field of the atom. Magnetism is inseparable part of our technology. There is numerous application of the permanent magnet such as Speaker, electric motors, relay switches, solenoid engines, memory storage, MRI scanner, smart phones, small fridge magnets, etc. Magnetic strength and magnetic field is the governing term of magnetism. It is well known to all; the magnetic field has the curved path but visualizing that shape is a difficult task. Calculating precise value of magnetic field at desired position is necessary in order to accomplish the project related to magnetism. Cyclotron and most of the particle accelerator uses magnetic field to accelerate the particles.

There are many methods for the calculation of magnetic field produce by the permanent magnet, which uses the numerical approximations using Legendre polynomial, greens function, Fourier expansion, hypergeometric series, etc. In this paper, I have used easier approach for the computation of the magnetic field due to permanent magnet by using triple integration, volume compensation for cylindrical magnet in the Cartesian co-ordinate system. This formula could even be used for the electromagnet in order to calculate the magnitude and direction of magnetic field at any desired point in space around it [2,3].

While prioritizing our knowledge to reducing friction and increasing the efficiency, I have come across an unusual technology called magnetic levitation [4]. With no interconnected parts, this system reduces the friction to almost zero neglecting the air friction [5,6]. It has become a scientific breakthrough in the field of modern engineering. This system has given its invaluable contribution in the field of transportation, aerospace, biomedical, etc. This paper includes all the modeling and simulations in MATLAB regarding one dimensional magnetic levitation [7,8].

Derivation

Scalar and vector potential

Any vector field can be represented into the sum of rotational and irrotational vector field.

In other words, a vector field ‘F’ can be represented by the summation of negative of Gradient of scalar potential and curl of its vector potential.

The scalar and vector potential of the magnetic field in equation 1 are

If the gradient of scalar potential and curl of vector potential are known then its vector function can be computed according to Helmholtz decomposition equation.

Where ɸ and A represent scalar potential and vector potential, respectively.

For a magnet divergence of a vector function is zero. So, it implies that there is no scalar potential ɸ in case of permanent magnetism. Hence, we are left with the curl of vector potential only as shown in equation 4.

Where, M is the magnetization constant of the material.

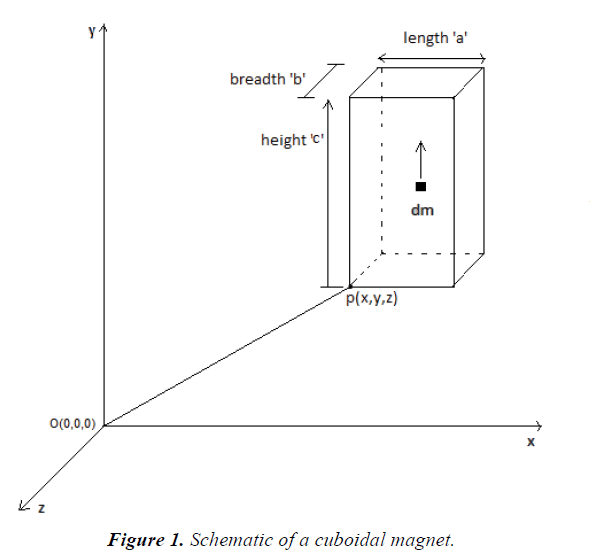
Considering the elementary volume, the above formula was integrated for whole volume of cuboid. The direction of the magnetic moment is taken upward; it should be noted that the direction of m is taken upward assuming the magnet is placed as shown in the figure below. It will also be correct when the magnet is placed upside down as in the Figure 1.

Figure 1. Schematic of a cuboidal magnet.

The integration of equation 5 was carried out using MATLAB and Mathematica and following results were obtained.

Assumptions:

The magnetic force experienced at a distance ‘d’ away from the magnet is given by the gradient of the dot product between magnetic dipole moment and the magnetic flux density.

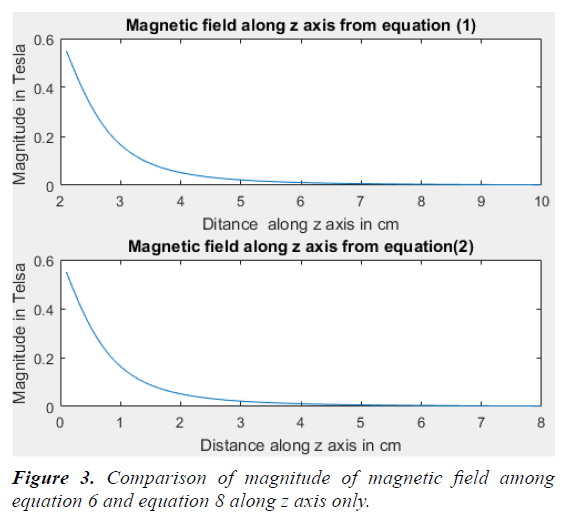
Comparison and Validity

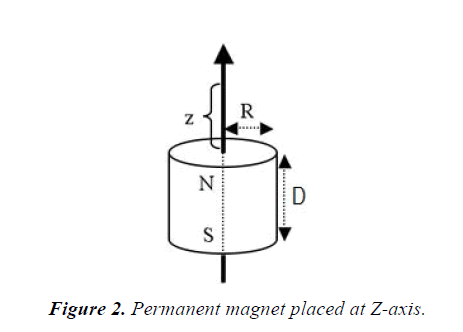
Equation 8 gives the formula for the B field on the symmetry axis of an axially magnetized cylinder magnet (disc or rod), which are commonly found in many text book of magnetism (Figure 2):

Figure 2. Permanent magnet placed at Z-axis.

M: Magnetization of the object.

B_r: Remanence field, independent of the magnet's geometry

z: Distance from a pole face on the symmetrical axis

D: Thickness (or height) of the cylinder

R: Semi-diameter (radius) of the cylinder

The unit of length can be selected arbitrarily, as long as it is the same for all lengths (Figure 3).

Figure 3. Comparison of magnitude of magnetic field among equation 6 and equation 8 along z axis only.

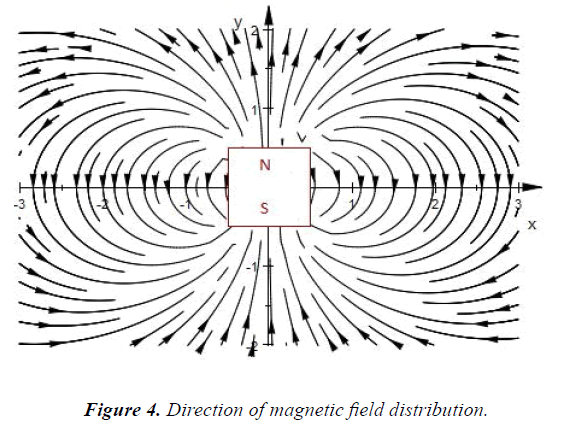
Magnetic Field Visualizaion

Magnetic levitation

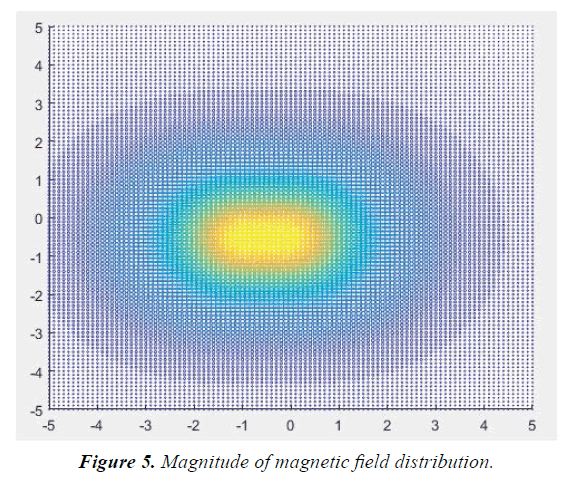
Ability to levitate itself using magnetic force of attraction or repulsion is simply called Magnetic levitation. Levitating object can be both ferromagnetic or permanent magnet based on the situation. Use of above three-dimensional equation for magnetic flux density in order to obtain the force on the levitating object would allow the device to control its input current to the solenoid. The above equation was reduced for one dimension and a ferromagnetic object of magnetization ‘M’ was levitated in Simulink, MATLAB (Figures 4 and 5).

Figure 4. Direction of magnetic field distribution.

Figure 5. Magnitude of magnetic field distribution.

Proposed system

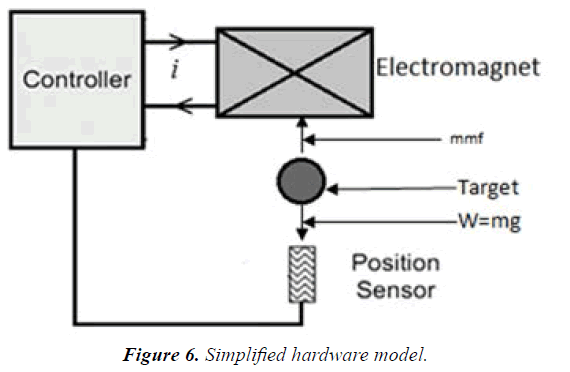
This is well explained by Figures 6 and 7.

Figure 6. Simplified hardware model.

Figure 7. VR model.

Modeling

Modeling of magnetic levitation is categorized into two parts:

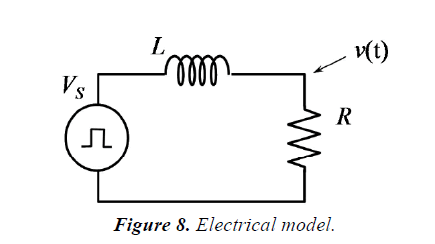
Electrical modeling (Figure 8)

Figure 8. Electrical model.

Laplace transform of above equation becomes;

Mathematical modeling

The mathematical equation governing the system is given by:

F_R =Resultant Force

F_g=Electromagnetic Force

F_g =Gravitational Force

The value of electromagnetic force is obtained by the below equation:

The equation of magnetic flux density is obtained for threedimensional space. It creates complexity in using this equation for one dimensional levitation.

is the one-dimensional force

is the magnetic force constant in (N.m²)/A²

For steady state condition, the resultant force on the ball must be zero. Hence,

Linearizing the equation 11 using Taylor Series about Δi=0, Δd=0

Some experimental data obtained during the experiment are as follows:

The transfer function of the ball and sensor system is thus given as:

The transfer functions from equation 9 and equation 14 are then used to simulate the levitation including a damping factor caused by the atmospheric air.

MATLAB Simulation

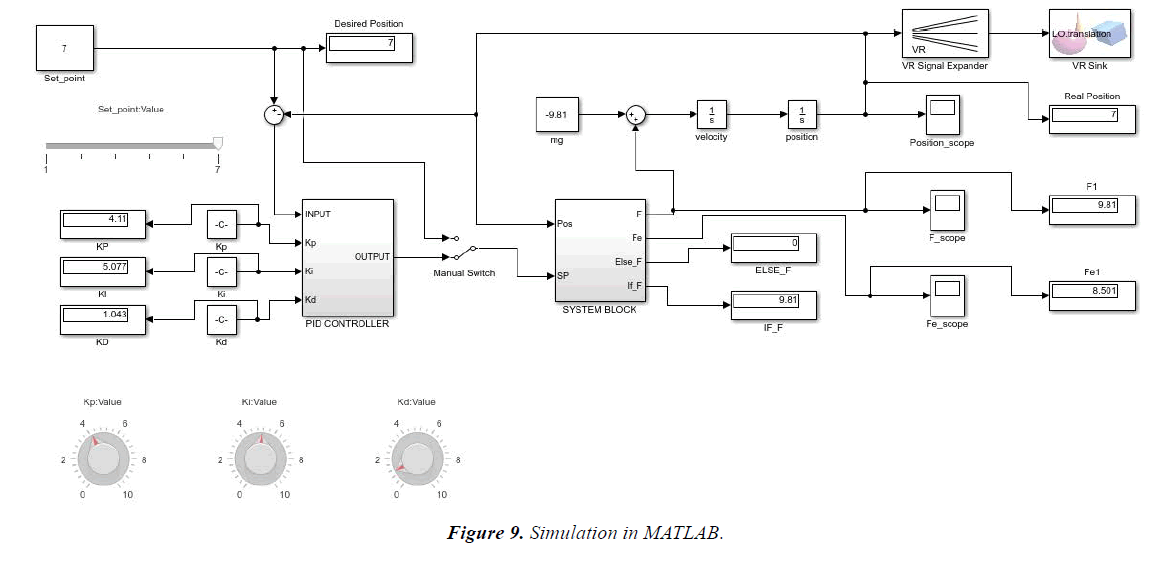
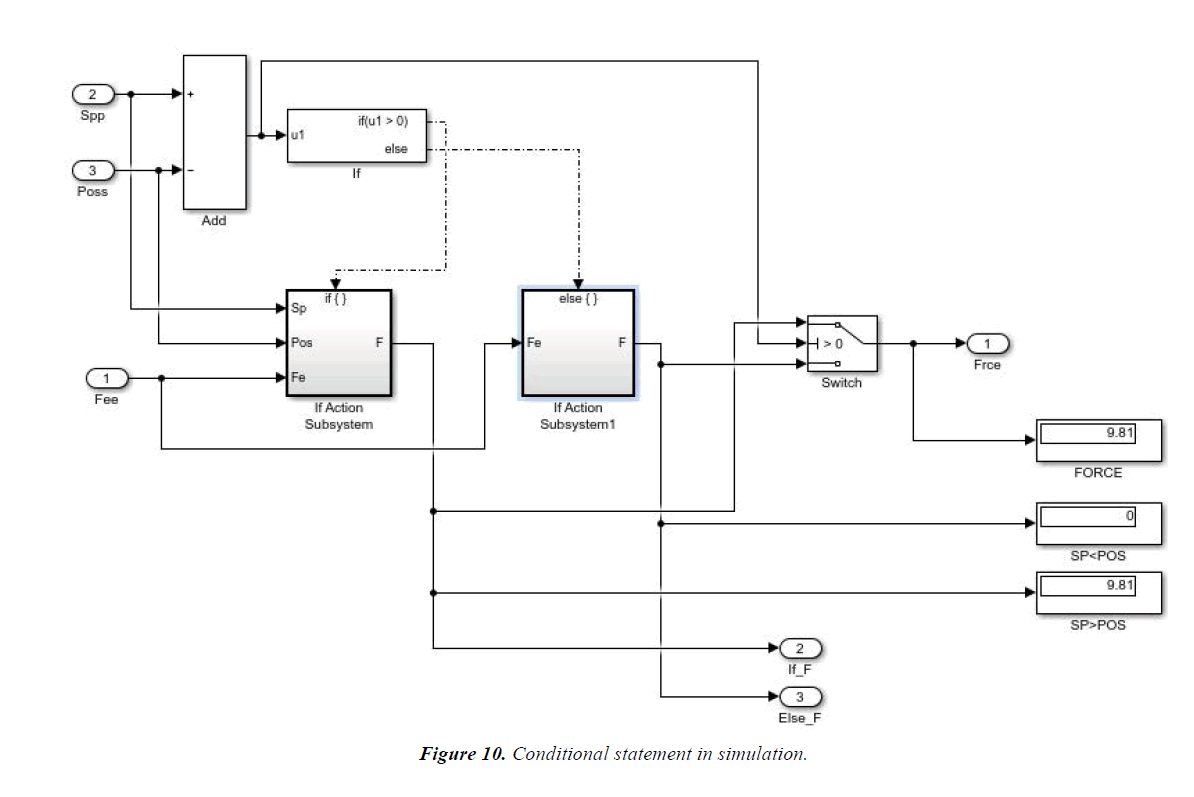
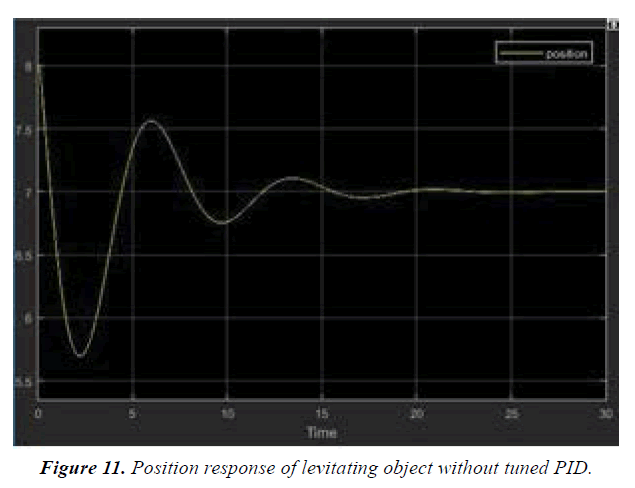
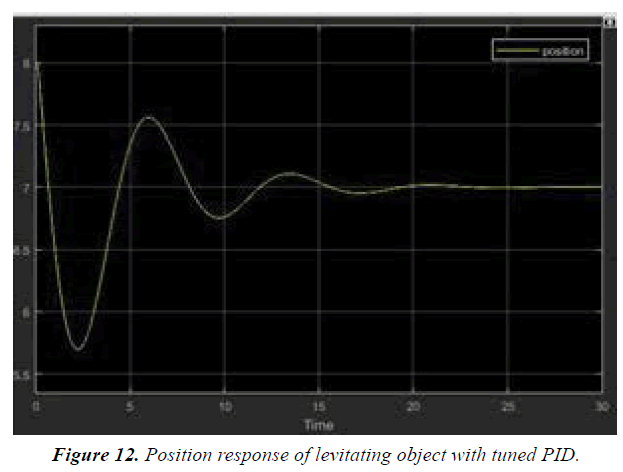
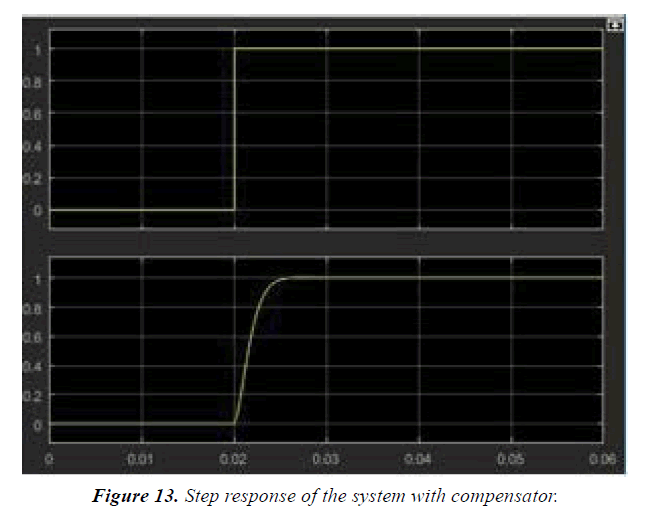
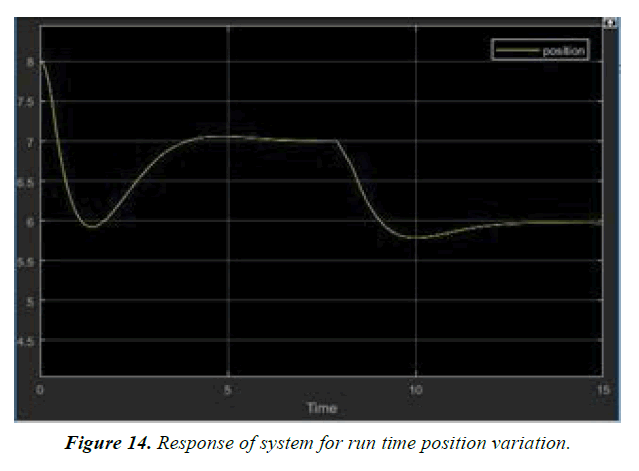
MATLAB simulations are well explained in Figures 9-14.

Figure 9. Simulation in MATLAB.

Figure 10. Conditional statement in simulation.

Figure 11. Position response of levitating object without tuned PID.

Figure 12. Position response of levitating object with tuned PID.

Figure 13. Step response of the system with compensator.

Figure 14. Response of system for run time position variation.

Hardware Simulation

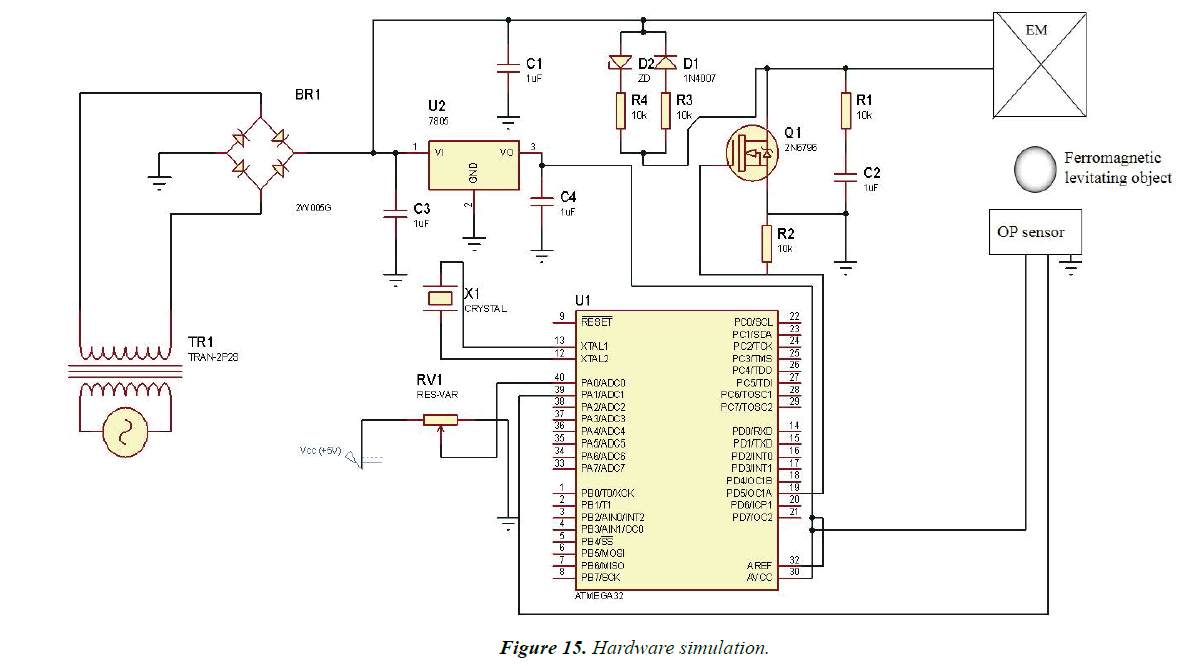
In Figure 15, hardware simulations are explained.

Figure 15. Hardware simulation.

Conclusion

This alternative approach of computing magnetic field provides one with easier and quicker way to compute magnetic field at any point on the space. It is equally true for the computation of magnetic field distribution of electromagnet. It provides an easier path for the calculation of field in the electric motor. Comparison with the existing formula and simplicity of the formula derivation assures the validity of the formula. Magnetic field due to different geometry electromagnet or permanent magnets such as solid cylinder, hollow cylinder, ring, etc., can also be figured out by using area compensation technique. The same equations can then be used to predict the flux or force values at certain position in any dimension to make the object levitate.

References

1. Selvaggi JP. Calculating the external magnetic field from permanent magnets in permanent magnet motors - An alternative method. IEEE Trans Magn. 2004;40(5):3278-85.
2. Camacho JM, Sosa V. Alternative approach to calculate the magnetic field of permanent magnets with azimuthal symmetry. Revista Mexicana de F´isica E. 2013;59:8-17.
3. Purcell EM, Morin DJ. Electricity and magnetism. Cambridge University Press. 2013.
4. Östman A. Demagnetization effects of assembling. Halbach Arrays.
5. Zijlstra H. Ferromagnetic materials. North Holland Publishing Company. 1982.
6. Zhang X, Mehrtash M, Khamesee MB. Dual axis motion control of a magnetic levitation system using hall-effect sensor. IEEE/ASME Trans Mechatron. 2016;21(2):1129-39.
7. Londhe AS. Antigravity electromagnetic levitation with position control system. Int Eng Res J.
8. https://www.brighthubengineering.com/machine-design/36161-what-is-magnetic-levitation/