Research Article - Biomedical Research (2017) Artificial Intelligent Techniques for Bio Medical Signal Processing: Edition-I

A computational model for biomedical system

¹Sathyabama University Chennai, India

²Department of Information Technology, St. Joseph’s College of Engineering, Chennai, India

*Corresponding Author:

Sungeetha D
Sathyabama University Chennai, India

Accepted date: January 16, 2017

Abstract

In this paper, we discuss about the specification of timed state transition systems that communicate by binary and rendezvous interactions. The observed approach unfolds the state machines according to synchronization and timing requirements. The unfolded state transition diagrams has been used to approximate a global time and to verify the safety, liveness and fairness properties of the system. A Master, Worker and Assembler of laser speckle image processing system in biomedical engineering are used as running example to illustrate the approach and properties.

Keywords

Timed CFSMs, Unfolded CFSMs, State explosion, Interleaving semantics, Partial-ordered semantics.

Introduction

With the increasing use of computers in medical imaging , there is a pressing need for designing more reliable systems. As a result, developing formal methods for the design and analysis of concurrent systems has become an active area in computer science and biomedical engineering research. Traditional testing method such as simulation is inadequate for developing bug-free complex and concurrent systems. One approach to ensure correctness is to employ automatic verification method. A verification formalism consists of [1]:

• A formal semantics to assign mathematical meaning to system components and its correctness criteria;

• A language for describing the constructs for combining the components;

• A specification language for expressing the correctness requirements;

• A verification algorithm to ensure that correctness criteria are fulfilled in every possible execution of the system.

Real-time system performances are used in medical image processing system. Failures in such systems can be very expensive and even life-threatening and consequently there is a great demand for formal methods that should be applied to real-time systems. Different formalisms have been proposed to reason reactive systems. These include process algebra, temporal logics, Petri Nets, automata theoretic techniques and partial-order models [1]. In the traditional approach for verification of concurrent programs, the correctness of the program is expressed by a formula in first-order temporal logic. The verification reduces to proving a theorem in a deductive system. Model-checking provides a different approach to check the properties of finite state systems [1-8]. In this approach, the global state transition graph is viewed as a finite Kripke structure. The specification of the system is given as a formula of a propositional temporal logic. The modelchecking algorithm decides whether a system meets the specification in all possible executions or not.

The model-checking approach used for program verification is probably the most exciting advance in the theory of program correctness in recent years. The main difficulty in using modelchecking approach is the state-space explosion problem. The size of the global state-transition graph grows exponentially with the number of components in the system. There are many ways to avoid this problem [1-8]. In this work, the partialordered unfoldings of CFSMs (Communicating finite state machine) are constructed to avoid the state-explosion in constructing a single total-ordered global-state transition graph (also known as product machine).the above method is achieved by simulating each local CFSMs in the presence of non-local CFSMs and performing the synchronizations. Section 2 defines the preliminaries of the CFSMs and their unfolding using a real time laser speckle image processing in biomedical image processing system.

Timed CFSMs and their Unfoldings

Here it is assumed that specification of n CFSMs are nonterminating [2]. The CFSMs interact by synchronous messagepassing via a binary rendezvous based on the seminal work of CSPs (Communicating Sequential Processes) [9,10]. The simultaneous n-ary (multiparty) interaction is split into a sequence of two party rendezvous interactions using a queue.

In a set of n communicating and non-terminating FSMs, each CFSM is defined as a 7-tuple:

Definition 1. A CFSM Fi = (s_0fi, S_fi, A_fi, C_fi, R_tfi, Rsync_fi, Rsync_0fi) where,

S_fi is the finite set of states of CFSM F_i, s_0fi ϵ S_fi being the initial state.

A_fi is the finite set of asynchronous and synchronous actions of F_i.

C_fi is the set of clock variables of F_i

R_tfi is a transition relation such that:

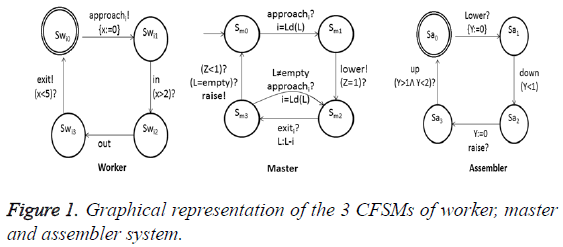
In i-transition (s_fi, a_fi, g_fi, u_fi, s’_fi) ϵ R^tfi, s_fi is called the input state and s’_fi the output state. a_fi is the action label, g_fi is the guard which is the enabling condition of the transition based on clock variables C_fi, (default being True), u_fi is the update statement again based on clock variables (default being Null statement) executed upon the transition. If the enabling condition g_fi is True, the transition is considered instantaneous and if g_fi is of the form (x_i ≥ t_i), x_i ϵ C_fi, the transition takes at least ti time units to enter the next state s’_fi from s_fi. In the case of a synchronous transition, the send action is denoted as A_fi! and the corresponding receive action as A_fi? in the partner CFSM F_j, j ≠ i.

• is a binary relation which relates the output states of synchronous transitions.

• relates the set of pairs of initial states: All the initial states are assumed to be in pairwise synchronous with each other to begin with.

• Figure 1 shows an example of worker, master and assembler CFSMs [11]. When there is more than one worker in a simultaneous approach, the master serves one worker at a time, making the other worker wait in a queue.

Figure 1: Graphical representation of the 3 CFSMs of worker, master and assembler system.

The unfolding of CFSMs

Definition 2: The unfolded CFSM M_i = (s_0i, S_i, A_i, C_i, R_ti, Rsync_i, Rsync_0i), whose 7-tuple entities are generated as instances of corresponding entities of CFSM F_i, i ϵ {1..n} unfolded in time.

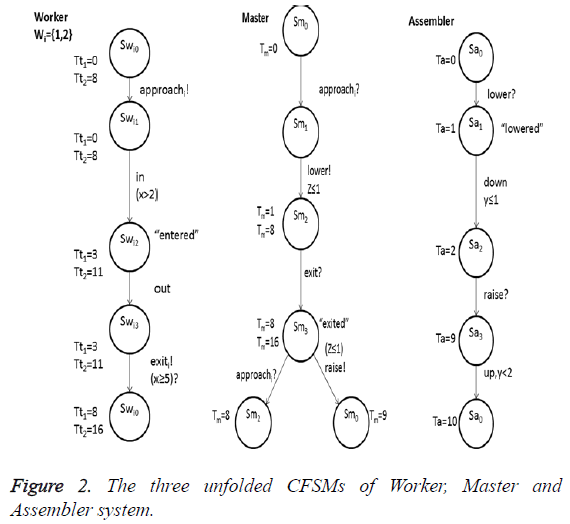
Figure 2 shows the unfolded CFSMs of the worker t_i, master and the assembler. The master is considered as the anchoring agent as it synchronizes both the worker agent and assembler agent/process. T_ti, T_m and T_a are the variables monitoring the local times of the worker, master and assembler agents, respectively. The local time of each agent at every state-entry, is initialized to zero. Thus T_ti=0, T_m=0 and T_a=0, respectively at states Sw_i0, Sm₀ and Sa₀. At every local output state entry, for instantaneous transition, the time remains the same as that of the input state entry. For non-instantaneous transition the local time is updated corresponding to the duration of the transition as dictated by its guard g_fi(C_fi). For instance, if the synchronous transition pair appri! and appr? respectively from states Sw₁₀ and Sm₀ are instantaneous then T_t1=0 and T_m=0 at the respective output states St₁₁ and Sm₁. At every rendezvous/ synchronization point, the state entry times of both synchronous output states are normalized to maximum of the corresponding local times. After the transition pair lower! and lower? from states Sm₁ and Sa₀ respectively, the local clock constraint of guard z<1 dictates Tm=1 at Sm2. Even though there is no such constraint for the assembler agent’s lower? action, the local time T_a at Sa₁ is normalized to the maximum one, viz., T_m=1, same as master. Thus the local time is propagated at synchronization point and becomes logically a semi-global time. Hence the anchoring agent master, propagates the worker’s local time to the assembler agent and vice versa. Rest of the local time updates are shown in Figure 2.

Figure 2: The three unfolded CFSMs of Worker, Master and Assembler system.

Well-founded, partially-ordered causality generation

When the CFSM graphs are unwinded in their mutual global environments into trees by simulating each of the former in their respective non-local environments, it tends to generate a global causality which is a partial-order. The global, temporal causality order is composed using the binary relations Rsync_i and R_i, i ϵ {1..n} as follows [2]:

≤ ::= (R_i U Rsync_i)*

The binary successor relation R_i is R_ti with input and output states related. The binary relation represents the partially ordered, and well-founded causality relation among the states of CFSMs in the unfolding based on their points of entry in time. The Rsynci relations capture the equality in time of the synchronous output states.

The unfolded timing diagram is shown in Figure 2. Each local state of the unfolding CFSM stores the local time, which is updated according to local clock constraint after asynchronous local transitions. After every synchronous transition, the local time is updated to the maximum of the two synchronizing FSMs. Thus, an approximate global time is synthesized by propagating the maximum advanced local times of the communicating FSMs.

Initially the worker-i is in state Sw_i0 and the master is in state Sm₀ and the assembler in Sa₀. The approach of the first worker is captured by the pair of transitions approachi! by the sending worker and approach? by the receiving master from the corresponding local states Sw_i0 and Sm₀ respectively. If there is more than one worker approaching simultaneously, one of them is selected from the head of the list/queue L and the others are made to wait in the queue. T_ti, the local time of worker ti is set to 0, T_ti=0, and similarly the local time of master is set to 0, T_m=0 after the instantaneous transition pair approach!/approach? reaching states Sw_i1 and Sm₁ respectively. Next, the master sends lower! signal to the assembler which receives it by its corresponding lower? transition within a maximum of 1 minute. Therefore at the end of lower!/lower? pair of synchronous transitions, the local times of master and assembler are, T_m=1 and T_a=1 at states Sm₂ and Sa₁ respectively. Next, the worker ti makes a local asynchronous transition in x>2 minutes. If T_ti=3, at state Sw_i2 following the local clock constrint of x>2. Then, worker t_i makes another local transition out which is instantaneous, reaching Sw_i3. The local time of worker t_i remains T_ti=3 in state Sw_i3 and so on. The remaining transitions and local times are shown in Figure 2. Because of the fact that the master is synchronizing with assembler and the worker t_i independently and at each synchronization point the local times are updated to the maximum, deducing the logical global time of the observer, observing all the three parties/processes [12-14].

The elimination of state-explosion due to nondeterministic interleaving in unfolded CFSMs

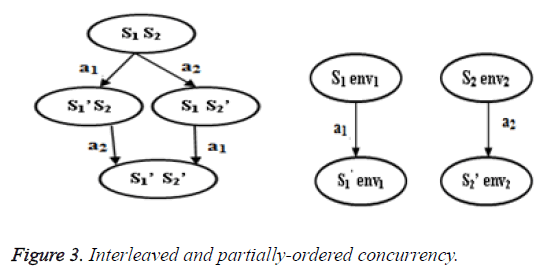
Consider a conventional product machine composed of two component CFSMs. Assume a state vector (s₁, s₂) of the product machine with s1 representing the state of CFSM₁ and s₂ representing that of CFSM₂. Consider two local/ asynchronous state transitions (s₁, a₁, s’₁) and (s₂, a₂, s’₂) of CFSM₁ and CFSM₂, respectively. In the traditional construction of the product machine, these two transitions are modeled by choosing either one of the two transitions to happen first followed by the other in sequence. This would lead to the following product machine state transitions as shown in Figure 3. Consisting of 2²=4 transitions representing the 2 independent local/asynchronous transitions of CFSM₁ and CFSM₂. To extend this representation of non-deterministic interleaving to n different local/asynchronous transitions of n respective CFSMs, CFSM₁, CFSM₂ … CFSM_n, it would need 2ⁿ transitions to represent n independent asynchronous transitions of the n CFSMs in the case of product machine. On the other hand, in the case of the unfolded CFSMS, the n local/ asynchronous transitions of the n CFSMs would be modeled by exactly n transitions. This is the main advantage of the partially-ordered CFSM unfoldings where the exponential explosion of states due to non-deterministic interleaving is avoided due to maintains of the locality of each CFSM.

Figure 3: Interleaved and partially-ordered concurrency.

Conclusion

A specification of timed CFSMs with a worker, assembler, master of laser speckle image processing system in biomedical engineering , is illustrated to specify and model-check the safety, liveness and fairness properties of a timed communicating agent. With the help of temporal logic verification model checking is to be done in author’s future work. The state-explosion problem of model-checking is eliminated by avoiding the product machine construction of interleaving semantics, using the unfolded CFSMs of partialorder semantics.

References

1. Alur R. Techniques for Automatic verification of Real-time systems, Ph.D. Thesis. Stanford Yniversity, 1991.
2. Narayanan VK. A state-oriented, Partial-order model and Logic for Distributed Systems Verification, Ph.D. Thesis, Concordia University, Montreal, 1997.
3. Clarke EM. Progress on the state-explosion problem in model-checking. Informatics 2001.
4. McMillan KL. Symbolic Model Checking: An approach to the state explosion problem, Ph.D. Thesis, 1992, CMU-CS-92-131.
5. Clarke EM, Emerson EA. Synthesis of synchronization skeletons for branching time temporal logic. Logic of Programs: Workshop, LNCS, 1981.
6. Clarke EM, Emerson EA, Sistla AP. Automatic verification of finite-state concurrent system using temporal logic. In Proceedings of the Tenth Annual ACM Symposium on Principles of Programming Languages (POPL), 1983.
7. Clarke EM, Grumberg O, Peled D. Model Checking. MIT Publishers, 1999.
8. Clarke EM, Schlingloff H. Model checking. Robinson J and VoronkovA , Ed, Handbook of Automated Reasoning. Elsevier, 2000.
9. Park J. A Theorem Prover for Boolean BI. ACM International conference on Principles of Programming Language POPL, 2013.
10. Hoare CAR. Communicating Sequential Processes. Prentice Hall 1984.
11. Yiqun C. Parallel and Distributed computing Techniques in Biomedical Engineering, Ph.D. Thesis, 2005.
12. Dakshinamurthy S, Narayanan V. A fully-distributed checkpointing-protocol for fault-tolerance in real-time distributed systems, in National IETE Conference, 2012.
13. Dakshinamurthy S, Narayanan V. A parallel algorithm for model-transformation of interactive state machine specification. Int J Wisdom Based Comput 2012.
14. Dakshinamurthy S, Narayanan V. A Model-checking Algorithm for Formal verification of Peer-to-peer Fault-Tolerant Networks, ICIWE 2013.
15. Yi W, Pettersson P, Daniels M. Automatic verification of real-time communicating systems by constraint-solving. In Formal Description Techniques VII. Springer US, 1995.