Review Article - Journal of Applied Mathematics and Statistical Applications (2018) Volume 1, Issue 1

Biharmonic timelike curves according to Bishop frame in Minkowski 4-space

*Corresponding Author:

Solouma EM
Faculty of Science Department of Mathematics Beni-Suef University Beni-Suef Egypt
Tel: +2 (082) 232 48 79
E-mail: emadms74@gmail.com

Accepted date: November 29, 2017

Citation: Solouma EM, Wageeda MM. Biharmonic timelike curves according to Bishop frame in Minkowski 4-space. J Appl Math Stat App. 2017;1(1):1-3.

Abstract

In the last decade there has been a growing interest in the theory of biharmonic maps which can be divided in two main research directions. On the one side, constructing the examples and classification results has become important from the differential geometric aspect. The other side is the analytic aspect from the point of view of partial differential equations, because biharmonic maps are solutions of a fourth order strongly elliptic semi linear PDE.Biharmonic curves γ : I ?⊂???→(N, h) of a Riemannian manifold are the solutions of the fourth order differential equation 3 R( , 3 ) 0, γ γ γ γ γ γ ′ ′ ∇ ′ − ′ ∇ ′ ′ = (1) where,∇ is the Levi-Civita connection on (N, h) and R is its curvature operator. As we shall detail in the next section, they arise from a variational problem and are a natural generalization of geodesics. In the last decade biharmonic curves have been extensively studied and classified in several spaces by analytical inspection of Equation 1 [1-15].Although much work has been done, the full understanding of biharmonic curves in a surface of the Euclidean threedimensional space is far from been achieved. As yet, we have a clear picture of biharmonic curves in a surface only in the case that the surface is invariant by the action of a one parameter group of isometries of the ambient space. For example, in the study by Caddeo et al. [4] it was proved that a biharmonic curve on a surface of revolution in the Euclidean space must be a parallel that is an orbit of the action of the group on the surface. This property was then generalized to invariant surfaces in a 3-dimensional manifold [15].In this paper, we study biharmonic non-lightlike curves according to Bishop frame in Minkowski 4-space 4 1 E . We give some characterizations for curvatures of a biharmonic non-lightlike curve in 4 1 E . This paper is organized as follows: Section 2 gives some basic concepts of the Frenet frame and Bishop frame of a curve in 4 1 E . Section 3 obtained some characterizations for curvature of these curves with respect to the principal curvature functions ( ) 1ks , ( ) ( ) 2 3 k s , k s according to Bishop frame

Keywords

Minkowski space-time, Biharmonic curve, Bishop frame, Heisenberg group.

Introduction

In the last decade there has been a growing interest in the theory of biharmonic maps which can be divided in two main research directions. On the one side, constructing the examples and classification results has become important from the differential geometric aspect. The other side is the analytic aspect from the point of view of partial differential equations, because biharmonic maps are solutions of a fourth order strongly elliptic semi linear PDE.

Biharmonic curves of a Riemannian manifold are the solutions of the fourth order differential equation

(1)

where,∇ is the Levi-Civita connection on (N, h) and R is its curvature operator. As we shall detail in the next section, they arise from a variational problem and are a natural generalization of geodesics. In the last decade biharmonic curves have been extensively studied and classified in several spaces by analytical inspection of Equation 1 [1-15].

Although much work has been done, the full understanding of biharmonic curves in a surface of the Euclidean threedimensional space is far from been achieved. As yet, we have a clear picture of biharmonic curves in a surface only in the case that the surface is invariant by the action of a one parameter group of isometries of the ambient space. For example, in the study by Caddeo et al. [4] it was proved that a biharmonic curve on a surface of revolution in the Euclidean space must be a parallel that is an orbit of the action of the group on the surface. This property was then generalized to invariant surfaces in a 3-dimensional manifold [15].

In this paper, we study biharmonic non-lightlike curves according to Bishop frame in Minkowski 4-space E⁴₁ . We give some characterizations for curvatures of a biharmonic non-lightlike curve in E⁴₁ . This paper is organized as follows: Section 2 gives some basic concepts of the Frenet frame and Bishop frame of a curve in E⁴₁ . Section 3 obtained some characterizations for curvature of these curves with respect to the principal curvature functions according to Bishop frame.

Preliminaries

The Minkowski space-time is four-dimensional Euclidean space provided with the Lorentzian inner product,

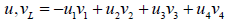
where 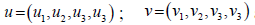are the rectangular coordinate system of E⁴₁ . Any vector u in E⁴₁ can be characterized as follows: the vector u is called spacelike, lightlike or timelike if ,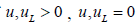 or 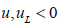respectively.The norm of a vector 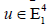is given by .

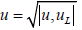Any arbitrary curve 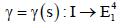is spacelike, timelike or lightlike (null), if all of its velocity vector 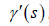are spacelike, timelike or lightlike (null), respectively. If 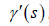, then γ is called unit speed curve [16]. For any unit speed timelike curve γ with Frenet-Serret frame { T,N,B₁ ,B₂ }, the Frenet formulas of the curve γ can be given as:

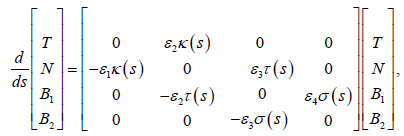
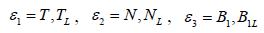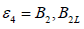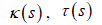where and , and and 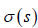are curvature, first and second torsion functions of the curve γ respectively. Here, we call the value of 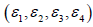as the character of Frenet frame of the curve γ .

The Bishop frame or parallel transport frame is an alternative approach to define a moving frame that is well defined even when the curve has vanished second derivative. We can transport an orthonormal frame along a curve simply by Bishoping each component of the frame [1-3,12,13]. The tangent vector and any convenient arbitrary basis for the remainder of the frame are used. The Bishop frame is expressed as

,

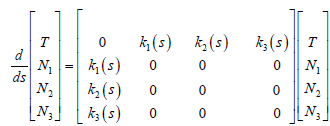where 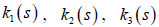are principal curvatures of the timelike curve according to the parallel frame and their expression as following:

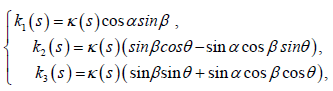
and

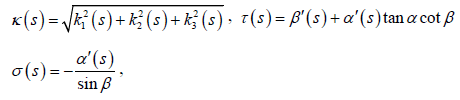
where 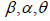are the spherical angle between the spacelike vectors N₃ and N₃ , spacelike vectors N₃ and N₃ , spacelike vectors N₃ and N3 respectively [9]. We shall call the set {T, N₁ ,N₂ ,N₃} as Bishop frame of γ in the Minkowski 4-spaceγ .

Discussion and Conclusion

Biharmonic non-lightlike curves according to Bishop frame in E⁴₁

In this section we give the notation of biharmonic non-lightlike curves in E⁴₁ according to Bishop frame. We also obtain some characterizations for curvature of these curves. Let 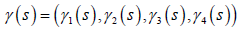be a unit speed timelike curve parametrized by arc-length in E⁴₁. The corresponding Bishop frame formula has the following form:

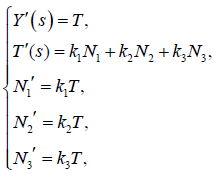(2)

where k₂ , k₂ and γ are the principal curvature functions according to Bishop frame of the curve γ . Now, the biharmonic equation for the curve γ reduces to

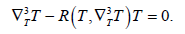(3)

Here, the curve γ is called a biharmonic curve if it is a solution of the Equation (3).

Theorem 3.1: Let γ be a unit speed timelike curve with nonzero principal curvature k₁ , k₂ and k₃ in E⁴₁ . Then γ is a biharmonic curve if and only if the following conditions are satisfied:

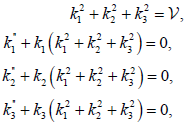(4)

where 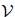is non-zero constant of integration.

Proof. Using the Bishop Equation (2) and biharmonic Equation (3), we obtain

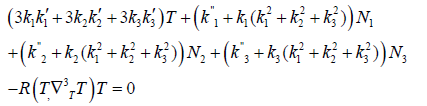(5)

In Minkowski 4-space E⁴₁ , the Riemannian curvature is zero, then we have

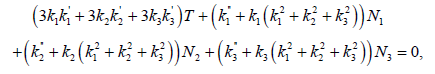(6)

By Equation (6), we see that the curve γ is a unit speed biharmonic curve if and only if

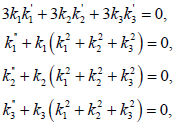(7)

Hence from the Equation (7), we get the result which complete our proof.

As a consequence of the Equation (4) we obtain the following Corollary;

Corollary 3.2: Let γ be a unit speed timelike curve with non-zero principal curvature k₁ , k₂ and k₃ in E⁴₁. Then γ is a biharmonic curve if and only if the following conditions are satisfied:

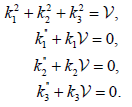(8)

Where 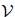is non-zero constant of integration.

Theorem 3.3: Let γ be a unit speed timelike curve with non-zero principal curvature k₁ , k₂ and k₃ in E⁴₁ . Then γ is a biharmonic curve if and only if the following conditions are satisfied:

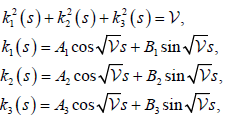(9)

where A_i , B_j for 1≤ i, j ≤ 3 and 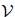are constants of integration. Proof. Directly, by using Equation (8), we have Equation (9).

Corollary 3.4: If A₁= A₂ = A₃ and B₁ = B₂ = B₃ , then we have k₁(s) = k₂(s) = k₃(s) .

Corollary 3.5: Let γ be a unit speed timelike biharmonic curve with non-zero principal curvature k₁ , k₂ and k₃ in E⁴₁ , then

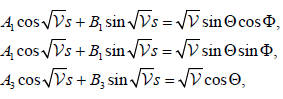
where 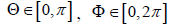and 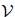A_i, B_j for 1≤ i, j ≤ 3 are constants of integration.

References

1. Bishop LR. There is more than one way to frame a curve. Amer Math Monthly. 1975;82:246-51.
2. Bukcu B, Karacan MK. Bishop frame of the spacelike curve with a spacelike principal normal in Minkowski 3-space. Commun Fac Sci Univ Ank Sér A1 Math Stat. 2008;57:13-22.
3. Bukcu B, Karacan MK. Bishop frame of the spacelike curve with a spacelike binormal in Minkowski 3-space. Selcuk J Appl Math. 2010;11:15-25.
4. Caddeo R, Montaldo S, Piu P. Biharmonic curves on a surface. Rend Math Appl. 2001;21:143-57.
5. Caddeo R, Oniciuc C, Piu P. Explicit formulas for non-geodesic biharmonic curves of the Heisenberg group. Rend Sem Mat Univ Politec Torino. 2004;62:265-277.
6. Caddeo R, Oniciuc C, Montaldo S, Piu P. The Euler-Lagrange method for biharmonic curves. Mediterr J Math. 2006;3:449-65.
7. Cho JT, Inoguchi JI, Lee JE. Biharmonic curves in 3-dimensional Sasakian space forms. Ann Math Pura Appl. 2007;186:685-701.
8. Dimitric I. Submanifolds of Em with harmonic mean curvature vector. Bull Inst Math Acad Sinica. 1992;20:53-65.
9. Erdogdu M. Parallel frame of non-lightlike curves in Minkowski space-time. Inte J of Geom Meth in Mod Physics. 2015;12:1550109.
10. Fetcu D. A note on biharmonic curves in Sasakian space forms. Ann Mat Pura Appl. 2010;189:591-603.
11. Fetcu D. Biharmonic Legendre curves in Sasakian space forms. J Korean Math Soc. 2008;45:393-404.
12. Andrew JH, Ma H. Bishop approach to curve framing. Indiana University Techreports. 1995:TR425.
13. Andrew JH, Ma H. Quaternion frame approach to streamline visualization. IEEE Transactions on Visualization and Computer Graphics. 1995;1.
14. Inoguchi JI, Lee JE. Affine biharmonic curves in 3-dimensional homogeneous geometries. Mediterr J Math. 2013;10:571-592.
15. Montaldo S, Onnis II. Biharmonic curves on an invariant surface. J Geom Phys. 2009;59:391-399.
16. O'Neill B. Semi-Riemannian geometry with applications to relativity. AP New York, USA. 1983.