Short Communication - Journal of Neurology and Neurorehabilitation Research (2017) Volume 2, Issue 1

Effect on coupling synchronization of Morris-Lecar neurons under time-delay.

*Corresponding Author:

Ruining Fan
School of Information Engineering Lanzhou University of Finance and Economics China
Tel: +86-0931-4938613
E-mail: 476266852@qq.com

Accepted date: May 23, 2017

Citation: Fan R, Zhang B. Effect on coupling synchronization of Morris-Lecar neurons under time-delay. J Neurol Neurorehabil Res. 2017;2(1):36-38.

Abstract

Based on the modified Morris-Lecar neuron mathematical model, this paper conducts the numerical calculation and simulation of the Morris-Lecar neuron mathematical model and studies the synaptic coupling synchronization of Morris-Lecar neurons under the effect of time-delay through the phase plane portrait, the time response graph and the synchronization difference graph. It is shown that the time-delay can promote the synchronization of the asynchronous coupled Morris-Lecar neurons and induce the coupling synchronization of the neurons, which illustrates time-delay has a certain effect on coupling neuronal system.

Keywords

Morris-Lecar neuron model, Coupling synchronization, Time-delay.

Introduction

The nervous system is an organ system which is composed of a network of neurons, a kind of specialized cell. The nervous system can sense the external stimuli. Time-delay is time delay, and its appearance triggers more complex nonlinear dynamic characteristics, so the influence of time delay on nonlinear dynamical behavior of the coupled neuron system has attracted more attention. With the deepening of research, neural networks such as time-delay Hopfield neural network [1], delayed bidirectional associative memory neural network [2], time-delay cellular neural network and time-delay Cohen-Grossberg [3] are put forward successively. The neural coupling system with time delay function also attracts a large number of experts and scholars at home and abroad to study and explore, and many meaningful results have been achieved [4,5]. This paper introduces the neuron model and related knowledge, introduces the related biological knowledge of the nervous system and the related techniques used in this paper. This paper establishes a Morris-Lecar chaotic neuron model with two neuronal electrical synapse couplings makes a dynamic analysis of the Morris- Lecar neuron model by numerical simulation and simulation and studies the effect of the electric synaptic coupling intensity of Morris-Lecar neuron model on the generation and release of electrical activity and synchronization of the system.

In this paper, the synchronization behavior of two neuron systems with time-delayed electrical synapse coupling is established. The dynamical behavior of the system is described by the following time-delayed differential equations:

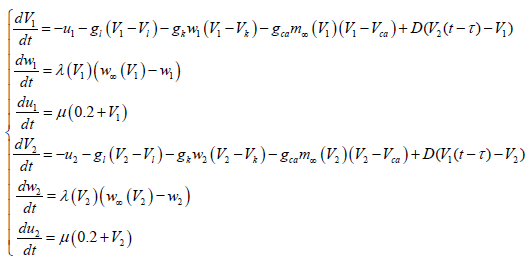(1)

In the equations above, the values of system parameters are as follows: V_ca=0.84, V₁=-0.5mV, V_k=-0.87mV, v₁=-0.01mV, v₂=-0.15mV, g₁=0.5 F/cm², g_k=2 F/cm², g_ca=1.2 F/cm². Drepresents the coupling strength,τ is on behalf of the ML neuronal information transmission delay, w is on behalf of the recovery variable. 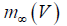and 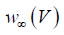represent the steadystate values of the open probability of the Ca²⁺ and k⁺ channels respectively.

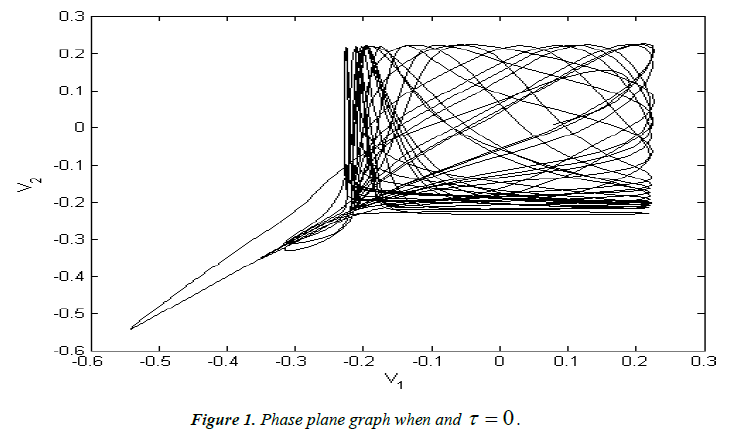
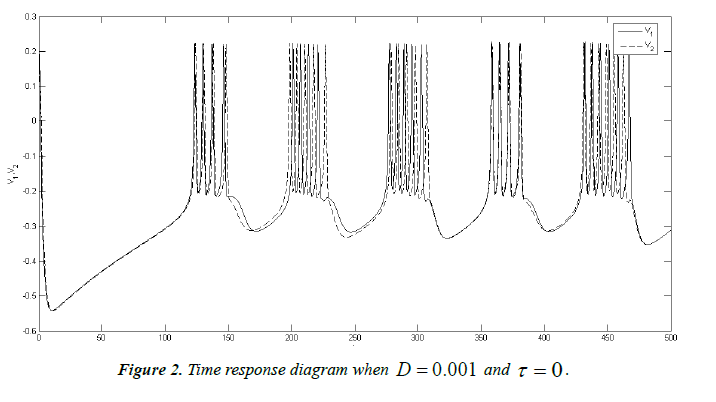
First, we study the synchronization of the neuron system without time-delay. Let t D = 0.001, (V₁ ,V₂ ) , and the phase plane portrait of the two electric synapse coupled ML neurons on the (V₁ ,V₂ ) plane can be obtained by the differential equation, which is shown as Figure 1.

Figure 1: Phase plane graph when and t = 0 .

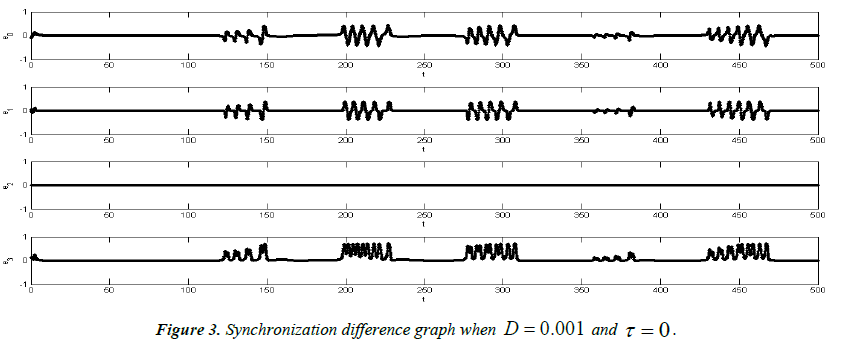
It can be seen from Figure 1, that the system is in an asynchronous state at this time and from Figure 2, that the values of V₁ and V₂ are different when they are at the same time, indicating that the two neurons do not reach the synchronized state. In order to better observe whether the two nerves are in the synchronous state or not, the introduction of neuron-coupled synchronization difference map is also made, as shown in Figure 3. It can be clearly seen from Figure 3 that the system is in the nonsynchronous state and the system is in a periodic discharge activity state but not synchronized.

Figure 2: Time response diagram when D = 0.001 and t = 0 .

Figure 3: Synchronization difference graph when D = 0.001 and t = 0 .

From the above analysis, it can be concluded that, within a certain range, the time delay can enhance the synchronization of the electrical synapse-coupled Morris-Lecar neurons and promote the coupling neurons to transfer from the asynchronous discharge patterns to the fully synchronous discharge patterns.

Conclusion

This paper studies the synergistic enhancement of electrical synaptic-coupled Morris-Lecar neuron system with timedelay. The results show that the appropriate time delay can enhance the occurrence of electrical synapse coupling neurons synchronization. These study results have important implications for the further understanding of the effects of time delay on the discharge pattern of the coupled neuron system.

Acknowledgement

This work was financially supported by the Scientific Research Project of Colleges and Universities in Gansu Province (No.2016B-051).

References

1. Mou S, Gao H, Lam J, et al.A new criterion of delay-dependent asymptotic stability for hopfield neural networks with time delay.IEEE Transactions on Neural Networks. 2008;19(3):532-5.
2. Sakthivel R, Vadivel P, Mathiyalagan K, et al. Design of state estimator for bidirectional associative memory neural networks with leakage delays. Inform Sci. 2015;296:263-74.
3. Ke Y, Miao C. Stability analysis of fractional-order Cohen-Grossberg neural networks with time delay. IntJ Comput Math. 2015;92(6):1102-13.
4. Buric N, Rankovic D, Todorovic K, et al. Mean field approximation for noisy delay coupled excitable neurons. Physica A Stat MechAppl.2010;389(19):3956-64.
5. Zhen B, Xu J. Simple zero singularity analysis in a coupled Fitzhugh-Nagumo neural system with delay. Neurocomputing. 2010;73(4-6):874-82.